第六章 特殊平行四边形 专项训练 特殊平行四边形中的中点四边形、将军饮马、距离和及规律探索问题研究(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形 专项训练 特殊平行四边形中的中点四边形、将军饮马、距离和及规律探索问题研究(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-04 20:13:02 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
专项训练 特殊平行四边形中的中点四边形、将军饮马、距离和
及规律探索问题研究
类型一 特殊平行四边形中的中点四边形
1.已知点 E,F,G,H分别为四边形ABCD 四条边中点,顺次连接EF,FG,GH,HE得到四边形EFGH.有下列说法:
①当四边形 ABCD 为平行四边形时,四边形 EFGH 是菱形
②当四边形 ABCD 为矩形时,四边形EFGH是菱形
③当 时,四边形 EFGH是正方形
④若四边形 EFGH 是正方形,则四边形ABCD一定是正方形.
其中正确的是____________(填序号).
2.如图,在四边形ABCD 中,E,F,G,H 分别是AD,AB,CB,CD 的中点,求证:四边形EFGH是矩形.
3.如图,四边形ABCD四条边上的中点分别为E,F,G,H,顺次连接EF,FG,GH,HE,得到四边形 EFGH(即四边形 ABCD 的中点四边形).
(1)四边形 EFGH 的形状是____________,并证明你的结论;
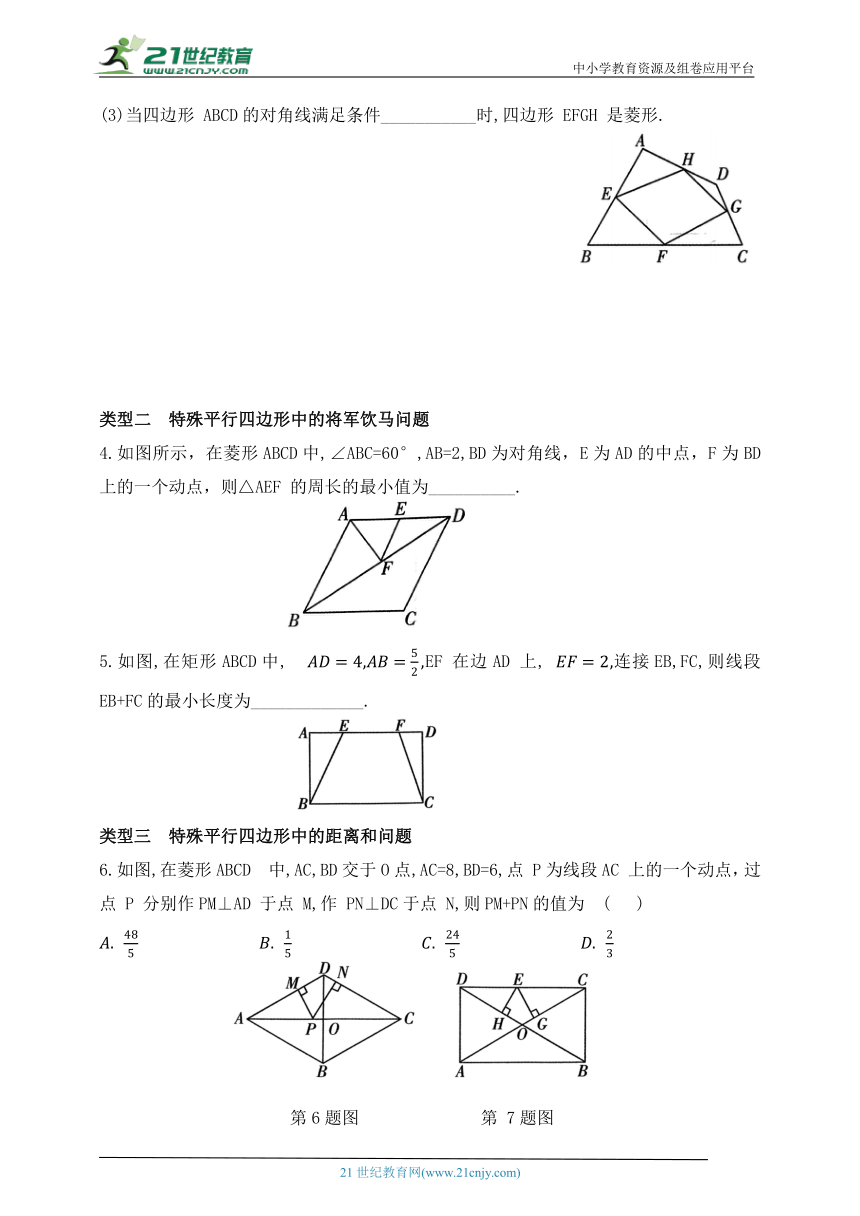
(2)当四边形 ABCD的对角线满足条件_________时,四边形 EFGH 是矩形;
(3)当四边形 ABCD的对角线满足条件___________时,四边形 EFGH 是菱形.
类型二 特殊平行四边形中的将军饮马问题
4.如图所示,在菱形ABCD中,∠ABC=60°,AB=2,BD为对角线,E为AD的中点,F为BD上的一个动点,则△AEF 的周长的最小值为__________.
5.如图,在矩形ABCD中, EF 在边AD 上, 连接EB,FC,则线段EB+FC的最小长度为_____________.
类型三 特殊平行四边形中的距离和问题
6.如图,在菱形ABCD 中,AC,BD交于O点,AC=8,BD=6,点 P为线段AC 上的一个动点,过点 P 分别作PM⊥AD 于点 M,作 PN⊥DC于点 N,则PM+PN的值为 ( )
第6题图 第 7题图
7.如图,在矩形 ABCD中,AC 和BD 相交于点O,AD=3,AB=4,点 E 是CD 边上一点,过点 E 作EH⊥BD 于点 H, EG⊥AC于点G,则 EH+EG的值是 ( )
A. 2.4 B. 2.5 C. 3 D. 4
8.如图,E 为边长为2 的正方形 ABCD的对角线BD上的一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点 Q,PR⊥BE 于点R,则 PQ+PR的值是 ( )
A. B. 1 D. 2
类型四 特殊平行四边形中的探索规律问题
9.如图,已知矩形 ABCD 的边长分别为a,b,进行如下操作:第一次,顺次连接矩形 ABCD 各边的中点,得到四边形第二次, 顺次 连接四边形各 边的中点,得到四边形如此反复操作下去,则第n次操作后,得到四边形 An Bn,Cn Dn的面积是 ( )
10.如图,正方形 ABCD 边长为1,以AC为边作第2个正方形 ACEF,再以 CF 为边作第3个正方形 FCGH……按照这样的规律作下去,第6个正方形的边长为 ( )
第10题图 第11题图
11.如图,矩形 ABCD 的对角线AC 与 BD 相交于点O,以AO,AB 为邻边作平行四边形 交 OB 于点 以 AB为邻边作平行四边形 若矩形 ABCD 的面积等于a,则四边形的面积=___________.
参考答案
1.②③
2.证明:如图所示,连接AC,BD,
∴BD 垂直平分AC,即
∵E,F 分别是 AD,AB的中点,∴EF 是 的中位线,∥BD,
同理得 ∥∥
∥∴四边形 EFGH 是平行四边形,
∴平行四边形 EFGH 是矩形.
3.解:(1)平行四边形;
证明:如图,连接BD.
∵E,H分别是AB,AD中点, ∥同理,得 ∥
∥∴四边形 EFGH 是平行四边形;
(2)互相垂直.理由如下:
如图,连接AC,BD.
∵E,F,G,H 分别为四边形ABCD 四条边上的中点,∥∥
又∵四边形 EFGH 是平行四边形,∴平行四边形 EFGH 是矩形;
(3)对角线相等.理由:∵E,F,G,H分别是边AB,BC,CD,DA 的中点,
∴四边形 EFGH为菱形.
6. C 7. A 8. A 9. A 10. C
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
专项训练 特殊平行四边形中的中点四边形、将军饮马、距离和
及规律探索问题研究
类型一 特殊平行四边形中的中点四边形
1.已知点 E,F,G,H分别为四边形ABCD 四条边中点,顺次连接EF,FG,GH,HE得到四边形EFGH.有下列说法:
①当四边形 ABCD 为平行四边形时,四边形 EFGH 是菱形
②当四边形 ABCD 为矩形时,四边形EFGH是菱形
③当 时,四边形 EFGH是正方形
④若四边形 EFGH 是正方形,则四边形ABCD一定是正方形.
其中正确的是____________(填序号).
2.如图,在四边形ABCD 中,E,F,G,H 分别是AD,AB,CB,CD 的中点,求证:四边形EFGH是矩形.
3.如图,四边形ABCD四条边上的中点分别为E,F,G,H,顺次连接EF,FG,GH,HE,得到四边形 EFGH(即四边形 ABCD 的中点四边形).
(1)四边形 EFGH 的形状是____________,并证明你的结论;
(2)当四边形 ABCD的对角线满足条件_________时,四边形 EFGH 是矩形;
(3)当四边形 ABCD的对角线满足条件___________时,四边形 EFGH 是菱形.
类型二 特殊平行四边形中的将军饮马问题
4.如图所示,在菱形ABCD中,∠ABC=60°,AB=2,BD为对角线,E为AD的中点,F为BD上的一个动点,则△AEF 的周长的最小值为__________.
5.如图,在矩形ABCD中, EF 在边AD 上, 连接EB,FC,则线段EB+FC的最小长度为_____________.
类型三 特殊平行四边形中的距离和问题
6.如图,在菱形ABCD 中,AC,BD交于O点,AC=8,BD=6,点 P为线段AC 上的一个动点,过点 P 分别作PM⊥AD 于点 M,作 PN⊥DC于点 N,则PM+PN的值为 ( )
第6题图 第 7题图
7.如图,在矩形 ABCD中,AC 和BD 相交于点O,AD=3,AB=4,点 E 是CD 边上一点,过点 E 作EH⊥BD 于点 H, EG⊥AC于点G,则 EH+EG的值是 ( )
A. 2.4 B. 2.5 C. 3 D. 4
8.如图,E 为边长为2 的正方形 ABCD的对角线BD上的一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点 Q,PR⊥BE 于点R,则 PQ+PR的值是 ( )
A. B. 1 D. 2
类型四 特殊平行四边形中的探索规律问题
9.如图,已知矩形 ABCD 的边长分别为a,b,进行如下操作:第一次,顺次连接矩形 ABCD 各边的中点,得到四边形第二次, 顺次 连接四边形各 边的中点,得到四边形如此反复操作下去,则第n次操作后,得到四边形 An Bn,Cn Dn的面积是 ( )
10.如图,正方形 ABCD 边长为1,以AC为边作第2个正方形 ACEF,再以 CF 为边作第3个正方形 FCGH……按照这样的规律作下去,第6个正方形的边长为 ( )
第10题图 第11题图
11.如图,矩形 ABCD 的对角线AC 与 BD 相交于点O,以AO,AB 为邻边作平行四边形 交 OB 于点 以 AB为邻边作平行四边形 若矩形 ABCD 的面积等于a,则四边形的面积=___________.
参考答案
1.②③
2.证明:如图所示,连接AC,BD,
∴BD 垂直平分AC,即
∵E,F 分别是 AD,AB的中点,∴EF 是 的中位线,∥BD,
同理得 ∥∥
∥∴四边形 EFGH 是平行四边形,
∴平行四边形 EFGH 是矩形.
3.解:(1)平行四边形;
证明:如图,连接BD.
∵E,H分别是AB,AD中点, ∥同理,得 ∥
∥∴四边形 EFGH 是平行四边形;
(2)互相垂直.理由如下:
如图,连接AC,BD.
∵E,F,G,H 分别为四边形ABCD 四条边上的中点,∥∥
又∵四边形 EFGH 是平行四边形,∴平行四边形 EFGH 是矩形;
(3)对角线相等.理由:∵E,F,G,H分别是边AB,BC,CD,DA 的中点,
∴四边形 EFGH为菱形.
6. C 7. A 8. A 9. A 10. C
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
