第六章 特殊平行四边形 章末复习(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形 章末复习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-04 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
章末复习
考点一 菱形的性质和判定
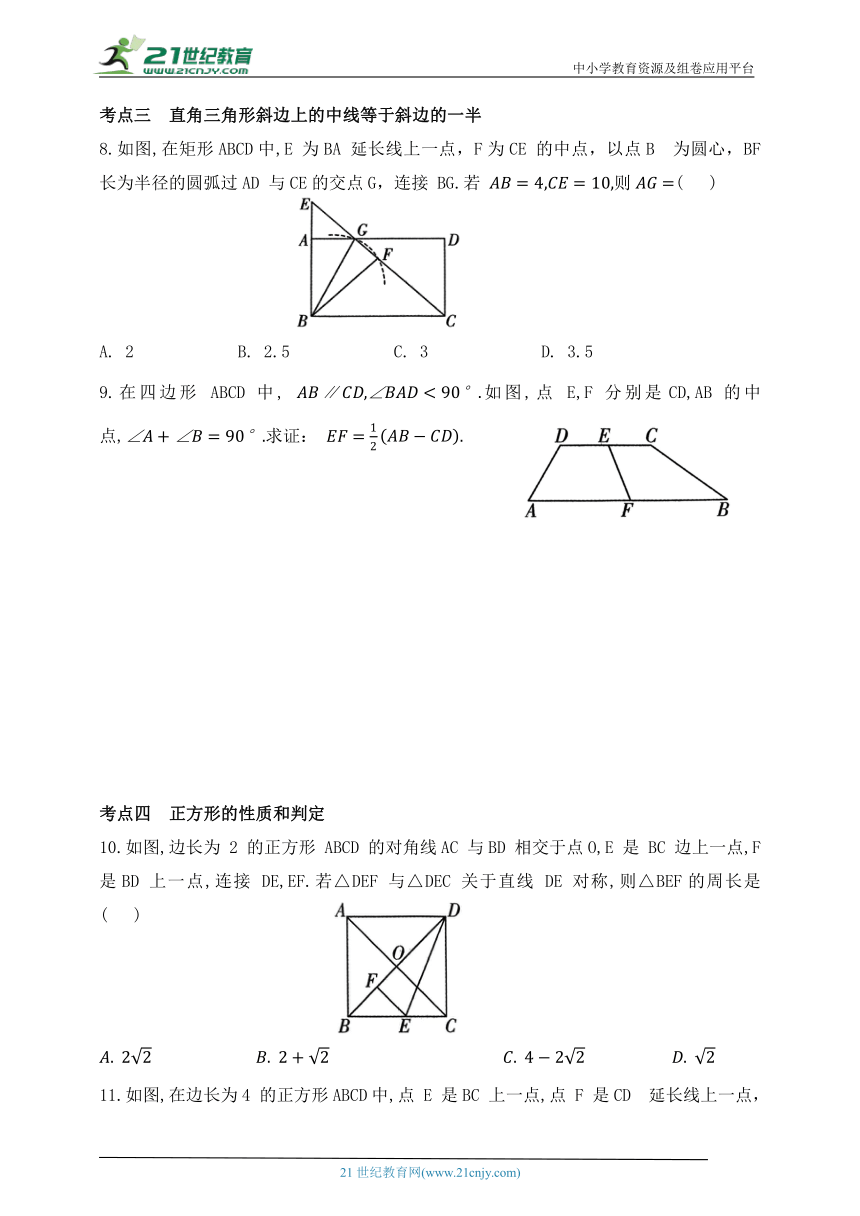
1.如图,四边形 ABCD 是菱形,于点 E,则AE 的长是 ( )
B. 6 D. 12
2.如图,在菱形ABCD中,点 P 在对角线 BD 上,过点 P 分别作CD,BC的平行线交BC,CD 于点 E,F.
(1)求证:
(2)连接AP,若 判断 PE与 PF的数量关系,并说明理由.
3.如图,在平行四边形ABCD中,对角线 AC,BD 相交于点 O,E,F,G分别是OC,OD,AB的中点.
(1)求证:
(2)连接AF,求证:四边形 AGEF 是菱形.
考点二 矩形的性质和判定
4.已知四边形 ABCD 是平行四边形,下列条件中,不能判定 ABCD为矩形的是 ( )
A.∠A=90° B.∠B=∠C C. AC=BD D. AC⊥BD
5.如图,在矩形ABCD 中,对角线 AC,BD相交于点O,∠ABD=60°,AB=2,则AC的长为 ( )
A. 6 B. 5 C. 4 D. 3
6.如图,在平行四边形ABCD 中,AE平分∠BAC,CF平分∠ACD.
(1)求证:△ABE≌△CDF;
(2)当△ABC 满足什么条件时,四边形AECF 是矩形 请写出证明过程.
7.如图,四边形 ABCD的对角线 AC 与 BD 相交于 点 O, AD ∥BC,∠ABC=90°,有下列条件:①AB∥CD, ②AD=BC.
(1)请从以上①②中任选1个作为条件,求证:四边形 ABCD 是矩形;
(2)在(1)的条件下,若AB=3,AC=5,求四边形ABCD的面积.
考点三 直角三角形斜边上的中线等于斜边的一半
8.如图,在矩形ABCD中,E 为BA 延长线上一点,F为CE 的中点,以点B 为圆心,BF长为半径的圆弧过AD 与CE的交点G,连接 BG.若 则( )
A. 2 B. 2.5 C. 3 D. 3.5
9.在四边形 ABCD 中, ∥如图,点 E,F 分别是CD,AB 的中点,求证:
考点四 正方形的性质和判定
10.如图,边长为 2 的正方形 ABCD 的对角线AC 与BD 相交于点O,E 是 BC 边上一点,F 是BD 上一点,连接 DE,EF.若△DEF 与△DEC 关于直线 DE 对称,则△BEF的周长是 ( )
11.如图,在边长为4 的正方形ABCD中,点 E 是BC 上一点,点 F 是CD 延长线上一点,连接AE,AF,AM 平分交CD 于点 M.若 则DM 的长度为 ( )
A. 2 B.
第11题图 第12题图
12.如图,在四边形ABCD 中,AE⊥BC于点E.若 则 BC的长是___________.
13.如图,正方形 ABCD的边长为4,点 G在BC上,且BG=3,DE⊥AG于点E,BF∥DE,交 AG于点 F.
(1)求证:
(2)求 EG的长.
易错点 忽略分类讨论致错
14.在矩形 ABCD中,若点 P 在AD 边上,连接BP,PC,△BPC 是以PB 为腰的等腰三角形,则PB的长为___________.
15.在正方形ABCD中,点 E 在对角线BD 上,点P 在正方形的边上(不与顶点重合),若 则在△AEP中, 的度数为_____________.
参考答案
1. A
2.解:(1)证明:∵四边形ABCD是菱形,∴AB=CD,∴∠CBD=∠CDB,
∵PE∥CD,PF∥BC,∴四边形 PECF 是平行四边形,∠CBD=∠FPD,
∴PE=CF,∠CDB=∠FPD,∴PF=DF,∴PE+PF=CF+DF=CD,∴AB=PE+PF;
理由:∵四边形 ABCD是菱形,∠ABC=60°,PE∥CD,
∴∠ABD=∠CBD=∠BDC=∠ADB=
∵∠APE=150°,∴∠APB=120°,∴∠DAP=90°,∴∠BAP=180°-∠APB-∠ABP=30°,
∴PA=PB,
连接 PC,如图,
∵AD=CD,∠ADP=∠CDP,DP=DP,∴△APD≌△CPD(SAS),
∴∠DCP=∠DAP=90°,PA=PC,∴∠CPE=∠DCP=90°,PB=PC,
∴∠PBE=∠PCE=30°,∴在 Rt△PEC中,
3.证明:(1)∵四边形 ABCD是平行四边形, 即BD=2BO,
又∵BD=2BC,∴OB=BC,
∵点 E 是OC 的中点,∴BE⊥AC;
(2)补全图形如图.
∵E,F分别是OC,OD的中点,
∵点G是 Rt△ABE斜边AB 上的中点,
∵四边形ABCD为平行四边形,∴AB=CD,AB∥CD,∴EG=EF=AG,EF∥AG,
∴四边形 AGEF 是菱形.
4. D 5. C
6.解:(1)证明:∵四边形 ABCD 是平行四边形,∴AB=CD,∠B=∠D,AB∥CD,
∴∠BAC=∠ACD,
∵AE平分∠BAC,CF平分∠ACD, ∴∠BAE=∠DCF,
在△ABE和△CDF中,∴△ABE≌△CDF(ASA);
(2)当△ABC 满足 AB = AC 时,四边形AECF 是矩形,理由如下:
由(1),得∠CAE=∠ACF,∴AE∥CF,
∵△ABE≌△CDF,∴AE=CF,∴四边形 AECF 是平行四边形.
又∵AB=AC,AE平分∠BAC,∴AE⊥BC,∴∠AEC=90°,∴平行四边形AECF 是矩形.
7.解:(1)选择①,证明:∵AD∥BC,AB∥CD,∴四边形 ABCD 是平行四边形,
∵∠ABC=90°,∴四边形 ABCD是矩形;
选择②,证明:∵AD∥BC,AD=BC,∴四边形ABCD 是平行四边形,
∵∠ABC=90°,∴四边形 ABCD 是矩形;
(2)∵四边形ABCD 是矩形,∴∠ABC=90°,
∵AB=3,AC=5,
8. C
9.证明:方法一:延长AD,BC相交于点P,连接PE,PF,
∥
又∵点 P,E,F 在PA 的同一侧,∴点 P,E,F在同一条直线上,
方法二:过点 E 分别作 ∥∥分别交AB 于点G,H.
∥∴四边形 DEGA 和四边形 BCEH 分别是平行四边形,
∴DE=AG,CE=BH,
∵点E,F 分别是CD,AB的中点,∴DE=CE,AF=BF,∴AG=BH,
∴AF-AG=BF-BH,即FG=FH,∴点 F 是GH 的中点,
∵EG∥AD,EH∥BC,∴∠A=∠1,∠B=∠2,
∵∠A+∠B=90°,∴∠1+∠2=90°,∴∠GEH=180°-(∠1+∠2)=90°,
又∵GH=AB-(AG+BH)=AB-(DE+CE)=AB-CD,
10. A 11. D 12. 7
13.解:(1)证明:∵DE⊥AG,BF∥DE,∴BF⊥AG,∴∠AED=∠BFA=90°,
∵四边形ABCD是正方形,∴AB=AD且∠BAD=∠ADC=90°,∴∠BAF+∠EAD=90°,
∵∠EAD+∠ADE=90°,∴∠BAF=∠ADE,
在△AFB和△DEA中,
∴△AFB≌△DEA(AAS),∴AE=BF;
(2)在 中, 根据勾股定理,得
由勾股定理,得
根据勾股定理,得
14.5 或6 解析:如图,在矩形ABCD中,
如图1,当 时,点 P 是 BC 的中垂线与AD 的交点,则
在 中,由勾股定理得
如图2,当 时, 也是以PB 为腰的等腰三角形.
综上所述,PB的长度是5 或6.
15.60°或90° 解析:如图,连接CE,
在正方形 ABCD中,∠ABE=45°,
∵∠AEB=105°,∴∠BAE=180°-45°-105°=30°,
①当点 在边AD上时,
是等边三角形,
②当点 在边CD 上时,
在△ADE 和△CDE中, ∴△ADE≌△CDE(SAS),
∴AE=CE,∠ECD=∠EAD=60°,∴AE=EP'=EP'=CE,
是等边三角形,
∵∠CED=∠AED=180°-105°=75°,∴∠DEP"=75°-60°=15°,
∴∠AEP"=75°+15°=90°,综上所述,∠AEP的度数为60°或90°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
章末复习
考点一 菱形的性质和判定
1.如图,四边形 ABCD 是菱形,于点 E,则AE 的长是 ( )
B. 6 D. 12
2.如图,在菱形ABCD中,点 P 在对角线 BD 上,过点 P 分别作CD,BC的平行线交BC,CD 于点 E,F.
(1)求证:
(2)连接AP,若 判断 PE与 PF的数量关系,并说明理由.
3.如图,在平行四边形ABCD中,对角线 AC,BD 相交于点 O,E,F,G分别是OC,OD,AB的中点.
(1)求证:
(2)连接AF,求证:四边形 AGEF 是菱形.
考点二 矩形的性质和判定
4.已知四边形 ABCD 是平行四边形,下列条件中,不能判定 ABCD为矩形的是 ( )
A.∠A=90° B.∠B=∠C C. AC=BD D. AC⊥BD
5.如图,在矩形ABCD 中,对角线 AC,BD相交于点O,∠ABD=60°,AB=2,则AC的长为 ( )
A. 6 B. 5 C. 4 D. 3
6.如图,在平行四边形ABCD 中,AE平分∠BAC,CF平分∠ACD.
(1)求证:△ABE≌△CDF;
(2)当△ABC 满足什么条件时,四边形AECF 是矩形 请写出证明过程.
7.如图,四边形 ABCD的对角线 AC 与 BD 相交于 点 O, AD ∥BC,∠ABC=90°,有下列条件:①AB∥CD, ②AD=BC.
(1)请从以上①②中任选1个作为条件,求证:四边形 ABCD 是矩形;
(2)在(1)的条件下,若AB=3,AC=5,求四边形ABCD的面积.
考点三 直角三角形斜边上的中线等于斜边的一半
8.如图,在矩形ABCD中,E 为BA 延长线上一点,F为CE 的中点,以点B 为圆心,BF长为半径的圆弧过AD 与CE的交点G,连接 BG.若 则( )
A. 2 B. 2.5 C. 3 D. 3.5
9.在四边形 ABCD 中, ∥如图,点 E,F 分别是CD,AB 的中点,求证:
考点四 正方形的性质和判定
10.如图,边长为 2 的正方形 ABCD 的对角线AC 与BD 相交于点O,E 是 BC 边上一点,F 是BD 上一点,连接 DE,EF.若△DEF 与△DEC 关于直线 DE 对称,则△BEF的周长是 ( )
11.如图,在边长为4 的正方形ABCD中,点 E 是BC 上一点,点 F 是CD 延长线上一点,连接AE,AF,AM 平分交CD 于点 M.若 则DM 的长度为 ( )
A. 2 B.
第11题图 第12题图
12.如图,在四边形ABCD 中,AE⊥BC于点E.若 则 BC的长是___________.
13.如图,正方形 ABCD的边长为4,点 G在BC上,且BG=3,DE⊥AG于点E,BF∥DE,交 AG于点 F.
(1)求证:
(2)求 EG的长.
易错点 忽略分类讨论致错
14.在矩形 ABCD中,若点 P 在AD 边上,连接BP,PC,△BPC 是以PB 为腰的等腰三角形,则PB的长为___________.
15.在正方形ABCD中,点 E 在对角线BD 上,点P 在正方形的边上(不与顶点重合),若 则在△AEP中, 的度数为_____________.
参考答案
1. A
2.解:(1)证明:∵四边形ABCD是菱形,∴AB=CD,∴∠CBD=∠CDB,
∵PE∥CD,PF∥BC,∴四边形 PECF 是平行四边形,∠CBD=∠FPD,
∴PE=CF,∠CDB=∠FPD,∴PF=DF,∴PE+PF=CF+DF=CD,∴AB=PE+PF;
理由:∵四边形 ABCD是菱形,∠ABC=60°,PE∥CD,
∴∠ABD=∠CBD=∠BDC=∠ADB=
∵∠APE=150°,∴∠APB=120°,∴∠DAP=90°,∴∠BAP=180°-∠APB-∠ABP=30°,
∴PA=PB,
连接 PC,如图,
∵AD=CD,∠ADP=∠CDP,DP=DP,∴△APD≌△CPD(SAS),
∴∠DCP=∠DAP=90°,PA=PC,∴∠CPE=∠DCP=90°,PB=PC,
∴∠PBE=∠PCE=30°,∴在 Rt△PEC中,
3.证明:(1)∵四边形 ABCD是平行四边形, 即BD=2BO,
又∵BD=2BC,∴OB=BC,
∵点 E 是OC 的中点,∴BE⊥AC;
(2)补全图形如图.
∵E,F分别是OC,OD的中点,
∵点G是 Rt△ABE斜边AB 上的中点,
∵四边形ABCD为平行四边形,∴AB=CD,AB∥CD,∴EG=EF=AG,EF∥AG,
∴四边形 AGEF 是菱形.
4. D 5. C
6.解:(1)证明:∵四边形 ABCD 是平行四边形,∴AB=CD,∠B=∠D,AB∥CD,
∴∠BAC=∠ACD,
∵AE平分∠BAC,CF平分∠ACD, ∴∠BAE=∠DCF,
在△ABE和△CDF中,∴△ABE≌△CDF(ASA);
(2)当△ABC 满足 AB = AC 时,四边形AECF 是矩形,理由如下:
由(1),得∠CAE=∠ACF,∴AE∥CF,
∵△ABE≌△CDF,∴AE=CF,∴四边形 AECF 是平行四边形.
又∵AB=AC,AE平分∠BAC,∴AE⊥BC,∴∠AEC=90°,∴平行四边形AECF 是矩形.
7.解:(1)选择①,证明:∵AD∥BC,AB∥CD,∴四边形 ABCD 是平行四边形,
∵∠ABC=90°,∴四边形 ABCD是矩形;
选择②,证明:∵AD∥BC,AD=BC,∴四边形ABCD 是平行四边形,
∵∠ABC=90°,∴四边形 ABCD 是矩形;
(2)∵四边形ABCD 是矩形,∴∠ABC=90°,
∵AB=3,AC=5,
8. C
9.证明:方法一:延长AD,BC相交于点P,连接PE,PF,
∥
又∵点 P,E,F 在PA 的同一侧,∴点 P,E,F在同一条直线上,
方法二:过点 E 分别作 ∥∥分别交AB 于点G,H.
∥∴四边形 DEGA 和四边形 BCEH 分别是平行四边形,
∴DE=AG,CE=BH,
∵点E,F 分别是CD,AB的中点,∴DE=CE,AF=BF,∴AG=BH,
∴AF-AG=BF-BH,即FG=FH,∴点 F 是GH 的中点,
∵EG∥AD,EH∥BC,∴∠A=∠1,∠B=∠2,
∵∠A+∠B=90°,∴∠1+∠2=90°,∴∠GEH=180°-(∠1+∠2)=90°,
又∵GH=AB-(AG+BH)=AB-(DE+CE)=AB-CD,
10. A 11. D 12. 7
13.解:(1)证明:∵DE⊥AG,BF∥DE,∴BF⊥AG,∴∠AED=∠BFA=90°,
∵四边形ABCD是正方形,∴AB=AD且∠BAD=∠ADC=90°,∴∠BAF+∠EAD=90°,
∵∠EAD+∠ADE=90°,∴∠BAF=∠ADE,
在△AFB和△DEA中,
∴△AFB≌△DEA(AAS),∴AE=BF;
(2)在 中, 根据勾股定理,得
由勾股定理,得
根据勾股定理,得
14.5 或6 解析:如图,在矩形ABCD中,
如图1,当 时,点 P 是 BC 的中垂线与AD 的交点,则
在 中,由勾股定理得
如图2,当 时, 也是以PB 为腰的等腰三角形.
综上所述,PB的长度是5 或6.
15.60°或90° 解析:如图,连接CE,
在正方形 ABCD中,∠ABE=45°,
∵∠AEB=105°,∴∠BAE=180°-45°-105°=30°,
①当点 在边AD上时,
是等边三角形,
②当点 在边CD 上时,
在△ADE 和△CDE中, ∴△ADE≌△CDE(SAS),
∴AE=CE,∠ECD=∠EAD=60°,∴AE=EP'=EP'=CE,
是等边三角形,
∵∠CED=∠AED=180°-105°=75°,∴∠DEP"=75°-60°=15°,
∴∠AEP"=75°+15°=90°,综上所述,∠AEP的度数为60°或90°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
