1.3 直角三角形全等的判定 课件(共21张PPT)
文档属性
| 名称 | 1.3 直角三角形全等的判定 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 835.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
第一章 直角三角形
1.3 直角三角形全等的判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
探索两个直角三角形全等的条件.
掌握两个直角三角形全等的条件(HL).
02
新知导入
1.三角形全等的判定定理有哪些
SAS ASA AAS SSS
2.两边及其中一边的对角对应相等的两个三角形全等吗
(即有SSA或ASS判定吗?)
不一定,没有SSA或ASS判定
3.如果其中一边所对的角是直角呢
03
新知探究
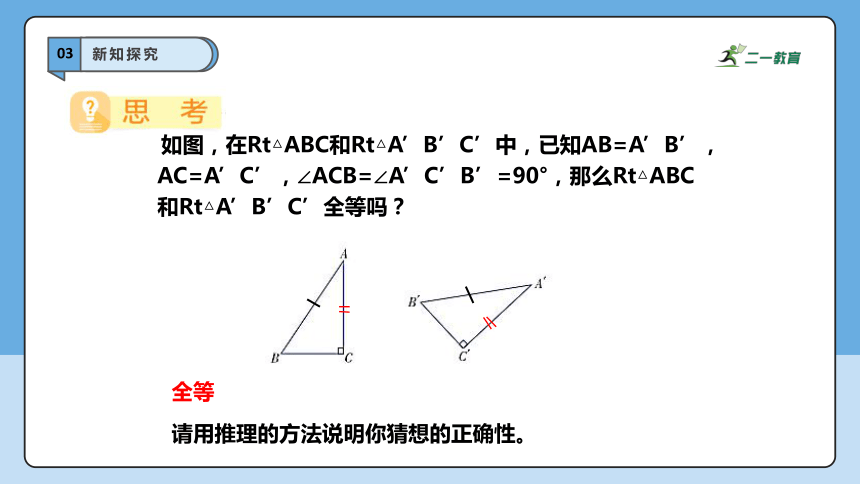
如图,在Rt△ABC和Rt△A’B’C’中,已知AB=A’B’,AC=A’C’,∠ACB=∠A’C’B’=90°,那么Rt△ABC和Rt△A’B’C’全等吗?
请用推理的方法说明你猜想的正确性。
全等
03
新知探究
分析:因为AB=A’B’,AC=A’C’,所以由勾股定理可得BC=B’C’,从而得出Rt△ABC ≌ Rt△A’B’C’
证明: ∵ ∠ACB=∠A’C’B’=90°,
AB=A’B’,AC=A’C’
∴BC= ,B’C’=
∴BC=B’C’
Rt△ABC和Rt△A’B’C’中
∴Rt△ABC ≌ Rt△A’B’C’(SSS)
03
新知探究
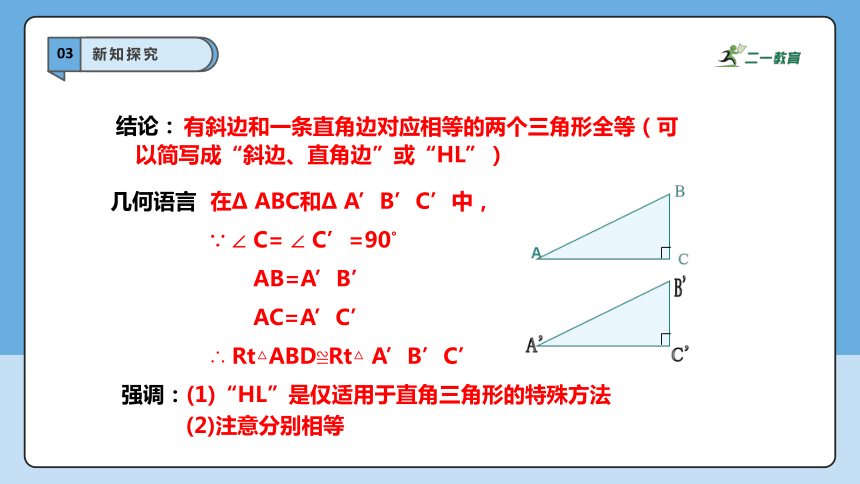
有斜边和一条直角边对应相等的两个三角形全等(可以简写成“斜边、直角边”或“HL”)
在Δ ABC和Δ A’B’C’中,
∵ ∠ C= ∠ C’=90°
AB=A’B’
AC=A’C’
∴ Rt△ABD≌Rt△ A’B’C’
结论:
几何语言
强调:(1)“HL”是仅适用于直角三角形的特殊方法
(2)注意分别相等
03
新知探究
直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,
还有直角三角形特殊的判定方法——“HL”.
1、总共有几种方法可以证明两个直角三角形全等?
新课探究
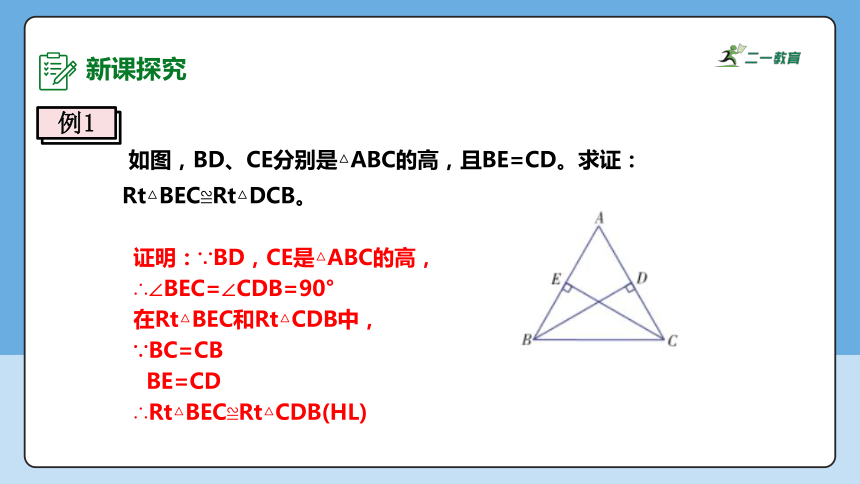
例1
如图,BD、CE分别是△ABC的高,且BE=CD。求证: Rt△BEC≌Rt△DCB。
证明:∵BD,CE是△ABC的高,
∴∠BEC=∠CDB=90°
在Rt△BEC和Rt△CDB中,
∵BC=CB
BE=CD
∴Rt△BEC≌Rt△CDB(HL)
03
新知讲解
例2
已知一直角边和斜边,求作直角三角形。
a
c
已知:线段a,c(c>a)
求作:Rt△ABC,使AB=c,BC=a
作法:(1)作∠MCN=90°。
A
C
M
N
(2)在CN上截取CB,使CB=a.
(3)以点B为圆心,以c为半径画弧,交CM于点A,连接AB。
04
课堂练习
【知识技能类作业】必做题:
1、在下列条件中,不能判定两个直角三角形全等的是( )
A.两条直角边对应相等
B.两个锐角对应相等
C.一个锐角和它所对的直角边对应相等
D.一条斜边和一条直角边对应相等
A
04
课堂练习
【知识技能类作业】选做题:
2.已知:如图,点B、F、C、E在同一直线上,BF=CE,AB⊥BE,DE⊥BE,垂足分别为B、E且AC=DF,连接AC、DF.
求证:∠A=∠D.
证明:∵BF=CE,
∴BF+FC=CE+FC.即BC=EF.
∵AB⊥BE,DE⊥BE,
∴∠B=∠E=90°.
在Rt△ABC与Rt△DEF中,∵AC=DF,BC=EF,
∴Rt△ABC≌Rt△DEF(HL).
∴∠A=∠D.
04
课堂练习
【综合拓展类作业】
3、如图,AD是△ABC的高,E为AC上一点,BE交AD于点F,若有BF=AC,FD=CD,试探究BE与AC的位置关系.
04
课堂练习
【综合拓展类作业】
解:BE与AC垂直.
理由:
∵AD是△ABC的高, ∴∠BDF=∠ADC=90°.
∴在Rt△BDF和Rt△ADC中,BF=AC,FD=CD.
∴Rt△BDF≌△Rt△ADC(HL).
∴∠DBF=∠DAC.
∵∠ADC=90°, ∴∠DAC+∠ACD=90°.
∴∠DBF+∠ACD=90°.
∴∠BEC=90°.
∴BE⊥AC.
05
课堂小结
直角三角形全等的判定
直角三角形全等的判定
一般三角形全等的识别
直角三角形全等的识别
SSS
SAS
ASA
AAS
HL
SAS
ASA
AAS
灵活运用各种方法证明直角三角形全等
06
作业布置
【知识技能类作业】必做题:
1.如图所示,AB=CD,AE⊥BD于点E,CF⊥BD于点F,AE=CF,则图中全等的三角形有( )
A.1对 B.2对 C.3对 D.4对
C
06
作业布置
【知识技能类作业】选做题:
2.用尺规作一个直角三角形,使其中一条边长为a,这条边所对的角为30°
作法:(1)作∠MCN=90°.
(2)在CN上截取CB,使CB=a.
(3)以B为圆心,以2a为半径画弧,交CM于点A,连接AB.
则△ABC为所求作的直角三角形.
06
作业布置
【综合拓展类作业】
6、已知:如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足,DE=BF.求证:AB∥CD.
证明:∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°.
在Rt△ABF和Rt△CDE中,AB=CD,DE=BF,
∴Rt△ABF≌Rt△CDE(HL).
∴∠ACD=∠CAB.
∴AB∥CD.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
1.3 直角三角形全等的判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
探索两个直角三角形全等的条件.
掌握两个直角三角形全等的条件(HL).
02
新知导入
1.三角形全等的判定定理有哪些
SAS ASA AAS SSS
2.两边及其中一边的对角对应相等的两个三角形全等吗
(即有SSA或ASS判定吗?)
不一定,没有SSA或ASS判定
3.如果其中一边所对的角是直角呢
03
新知探究
如图,在Rt△ABC和Rt△A’B’C’中,已知AB=A’B’,AC=A’C’,∠ACB=∠A’C’B’=90°,那么Rt△ABC和Rt△A’B’C’全等吗?
请用推理的方法说明你猜想的正确性。
全等
03
新知探究
分析:因为AB=A’B’,AC=A’C’,所以由勾股定理可得BC=B’C’,从而得出Rt△ABC ≌ Rt△A’B’C’
证明: ∵ ∠ACB=∠A’C’B’=90°,
AB=A’B’,AC=A’C’
∴BC= ,B’C’=
∴BC=B’C’
Rt△ABC和Rt△A’B’C’中
∴Rt△ABC ≌ Rt△A’B’C’(SSS)
03
新知探究
有斜边和一条直角边对应相等的两个三角形全等(可以简写成“斜边、直角边”或“HL”)
在Δ ABC和Δ A’B’C’中,
∵ ∠ C= ∠ C’=90°
AB=A’B’
AC=A’C’
∴ Rt△ABD≌Rt△ A’B’C’
结论:
几何语言
强调:(1)“HL”是仅适用于直角三角形的特殊方法
(2)注意分别相等
03
新知探究
直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,
还有直角三角形特殊的判定方法——“HL”.
1、总共有几种方法可以证明两个直角三角形全等?
新课探究
例1
如图,BD、CE分别是△ABC的高,且BE=CD。求证: Rt△BEC≌Rt△DCB。
证明:∵BD,CE是△ABC的高,
∴∠BEC=∠CDB=90°
在Rt△BEC和Rt△CDB中,
∵BC=CB
BE=CD
∴Rt△BEC≌Rt△CDB(HL)
03
新知讲解
例2
已知一直角边和斜边,求作直角三角形。
a
c
已知:线段a,c(c>a)
求作:Rt△ABC,使AB=c,BC=a
作法:(1)作∠MCN=90°。
A
C
M
N
(2)在CN上截取CB,使CB=a.
(3)以点B为圆心,以c为半径画弧,交CM于点A,连接AB。
04
课堂练习
【知识技能类作业】必做题:
1、在下列条件中,不能判定两个直角三角形全等的是( )
A.两条直角边对应相等
B.两个锐角对应相等
C.一个锐角和它所对的直角边对应相等
D.一条斜边和一条直角边对应相等
A
04
课堂练习
【知识技能类作业】选做题:
2.已知:如图,点B、F、C、E在同一直线上,BF=CE,AB⊥BE,DE⊥BE,垂足分别为B、E且AC=DF,连接AC、DF.
求证:∠A=∠D.
证明:∵BF=CE,
∴BF+FC=CE+FC.即BC=EF.
∵AB⊥BE,DE⊥BE,
∴∠B=∠E=90°.
在Rt△ABC与Rt△DEF中,∵AC=DF,BC=EF,
∴Rt△ABC≌Rt△DEF(HL).
∴∠A=∠D.
04
课堂练习
【综合拓展类作业】
3、如图,AD是△ABC的高,E为AC上一点,BE交AD于点F,若有BF=AC,FD=CD,试探究BE与AC的位置关系.
04
课堂练习
【综合拓展类作业】
解:BE与AC垂直.
理由:
∵AD是△ABC的高, ∴∠BDF=∠ADC=90°.
∴在Rt△BDF和Rt△ADC中,BF=AC,FD=CD.
∴Rt△BDF≌△Rt△ADC(HL).
∴∠DBF=∠DAC.
∵∠ADC=90°, ∴∠DAC+∠ACD=90°.
∴∠DBF+∠ACD=90°.
∴∠BEC=90°.
∴BE⊥AC.
05
课堂小结
直角三角形全等的判定
直角三角形全等的判定
一般三角形全等的识别
直角三角形全等的识别
SSS
SAS
ASA
AAS
HL
SAS
ASA
AAS
灵活运用各种方法证明直角三角形全等
06
作业布置
【知识技能类作业】必做题:
1.如图所示,AB=CD,AE⊥BD于点E,CF⊥BD于点F,AE=CF,则图中全等的三角形有( )
A.1对 B.2对 C.3对 D.4对
C
06
作业布置
【知识技能类作业】选做题:
2.用尺规作一个直角三角形,使其中一条边长为a,这条边所对的角为30°
作法:(1)作∠MCN=90°.
(2)在CN上截取CB,使CB=a.
(3)以B为圆心,以2a为半径画弧,交CM于点A,连接AB.
则△ABC为所求作的直角三角形.
06
作业布置
【综合拓展类作业】
6、已知:如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足,DE=BF.求证:AB∥CD.
证明:∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°.
在Rt△ABF和Rt△CDE中,AB=CD,DE=BF,
∴Rt△ABF≌Rt△CDE(HL).
∴∠ACD=∠CAB.
∴AB∥CD.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
