浙教版八年级上册期末数学复习提高卷2(含解析)
文档属性
| 名称 | 浙教版八年级上册期末数学复习提高卷2(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 21:07:47 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024学年八年级上册数学期末复习提高卷2(浙教版附答案)
一、选择题:(本题共10小题,每小题3分,共30分)
1. 等腰三角形的底边长为16,则腰长的取值可以为( )
A. 6 B. 7 C. 8 D. 9
2. 若关于的方程的解为正实数,则的取值范围是( )
A. B. C. D.
3. 如图,已知点A(2,2).若点P在y轴上,且△APO是等腰三角形,则点P的坐标不可能是( )
A. B. C. (0,-4) D. (0,4)
如图,已知直线与相交于点P,点P的横坐标为-1,则关
于不等式的解在数轴上表示正确的是( )
5.如图,在Rt△ABC中,AB=9,BC=6,∠B=,将△ABC折叠,使A与BC的中点D重合,折痕为MN,则DN的长为( )
A. 4 B. 5 C. 6 D. 7
6. 如图,点D在AC 上,点B在AE上,△ABC≌△DBE,且∠BDA=∠A,∠A:C=5:3.则∠CBE=( )
A. B. C. D.
7.如图所示,△ABC的面积为10,AP垂直于∠ABC的平分线BP于点P,则△PBC的面积为( )
A. B. C. 4 D.
如图,已知点C(1,0),直线与两坐标轴分别交于A、B两点,D、E分别是AB、OA上的动点.则△CDE周长的最小值是( )
B. C. D.
8个边长为2的正方形如图摆放在平面直角坐标系中,经过原点的一条直线将这8个正方形分成面积相等的两部分,则该直线的函数解析式为( )
A. B. C. D.
在平面直角坐标系中,已知A(-1,1)、B(3,3),直线与线段AB的延长线(交点不包括B)相交.则实数的取值范围为( )
B. C. 或 D.
二、填空题:(本题共6小题,每小题3分,共18 分)
11.若点在第二象限,则的取值范围是 .
12. 若一个直角三角形的两条边长分别为3和4,则斜边上的中线长为 .
13. 在平面直角坐标系中,点A(-4,2)、B(2,4)、C(m,n)在同一直线上,若m与n互为倒数,则= .
14. 若方程组的解满足,则的取值范围是 .
15. 已知Rt△ABC中,∠C=90°,AC=3,BC=4,将它的一个锐角翻折,使该锐角顶点落在其对边的中点D处,折痕交另一直角边于点E,交斜边于点F,则△CDE的周长为________.
如图,在等腰△ABC中,AB=AC=8,∠BAC=,AG是底边BC上的高,在AG 的延长线上有一个动点D,连接CD,作∠CDE=,交AB的延长线于点E,∠CDE的角平分线交AB于F.则在点D运动过程中,线段EF的最小值为 .
三、计算题:(本题有8小题,共52分)
17(本题5分).若关于的一元一次不等式组的解集为,求的取值范围.
18(本题7分)在平面直角坐标系中,我们把横、纵坐标都是整数的点称为整点,把顶点都是整点的三角形称为整点三角形.如图,已知整点A(2,2)、B(3,5),请在所给的网格区域(含边界)内按要求画出整点三角形.
在图1中画出以AB为一条直角边的等腰直角三角形ABC;
在图2中画出一个△OBD,使得△OBD的面积等于5,且使点A在△OBD的内部.
19(本题7分)如图,直线AB与轴、y轴分别相较于点、B(0,4),M是OB上一点,若将△ABM沿AM折叠,则点B恰好落在轴上的点处,求:
点的坐标;
△ABM的面积.
20(本题7分)在平面直角坐标系中有点,实数满足以下两个等式:,.
当时,求点P到轴的距离;
若点P落在第二、第四象限的角平分线上,求点P的坐标.
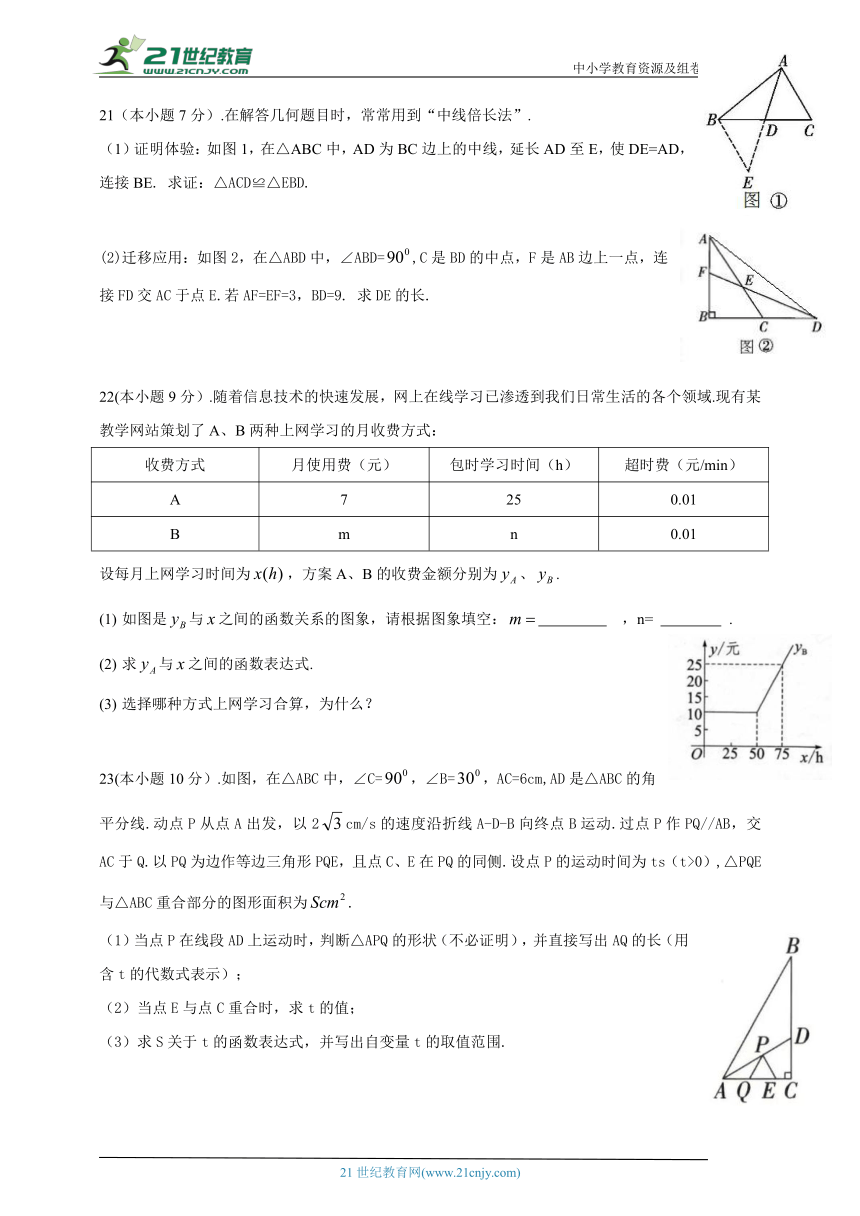
21(本小题7分).在解答几何题目时,常常用到“中线倍长法”.
(1)证明体验:如图1,在△ABC中,AD为BC边上的中线,延长AD至E,使DE=AD,连接BE. 求证:△ACD≌△EBD.
(2)迁移应用:如图2,在△ABD中,∠ABD=,C是BD的中点,F是AB边上一点,连接FD交AC于点E.若AF=EF=3,BD=9. 求DE的长.
22(本小题9分).随着信息技术的快速发展,网上在线学习已渗透到我们日常生活的各个领域.现有某教学网站策划了A、B两种上网学习的月收费方式:
收费方式 月使用费(元) 包时学习时间(h) 超时费(元/min)
A 7 25 0.01
B m n 0.01
设每月上网学习时间为,方案A、B的收费金额分别为、.
如图是与之间的函数关系的图象,请根据图象填空: ,n= .
求与之间的函数表达式.
选择哪种方式上网学习合算,为什么?
23(本小题10分).如图,在△ABC中,∠C=,∠B=,AC=6cm,AD是△ABC的角平分线.动点P从点A出发,以2cm/s的速度沿折线A-D-B向终点B运动.过点P作PQ//AB,交AC于Q.以PQ为边作等边三角形PQE,且点C、E在PQ的同侧.设点P的运动时间为ts(t>0),△PQE与△ABC重合部分的图形面积为.
(1)当点P在线段AD上运动时,判断△APQ的形状(不必证明),并直接写出AQ的长(用含t的代数式表示);
(2)当点E与点C重合时,求t的值;
(3)求S关于t的函数表达式,并写出自变量t的取值范围.
参考答案
选择题:1. D 提示:设腰长为,则,.故选D 2. D 提示:,,,.由题意可知,,.故选D. 3. C 提示:对于选项C:作AM⊥轴于M,若点P坐标为(0,-4),则OP=4..而.又∠AOP>,∴AP为△AOP的最大边,∴AP>OP>OA.∴△APO不是等腰三角形,故选C. 4. C 提示:∵当时,,∴不等式的解集为.故选C. 5. B 提示:设DN=,由对折可知AN=DN=.∵AB=9,∴BN=9.∵BC=6,D为BC的中点,∴BD=3.∵∠B=,,,解得.∴DN=5,故选B. 6. A 提示:由∠A:∠C=5:3可设∠A=,∠C=3,∵∠BDA=∠A,∴∠BDA=5.∵△ABC≌△DBE,∴∠E=∠C=,∠BDE=∠A=.∴∠ADE=∠BDA+∠BDE=.∵∠A+∠ADE+∠E=,,.∴∠CBE=∠A+∠C=.故选A. 7.D 提示:延长AP交BC于M,则△ABP≌△MBP,∴AP=MP.∴,.
.故选D.
8.B 提示:作点C关于直线的对称点M,作点C关于y轴的对称点N,则M(6,5)、N(-1,0).设直线MN交y轴于E,交直线于D,此时△CDE取得最小值.此时,△CDE周长=CD+CE+DE=MD+NE+DE=MN=.故选B.
9. A 提示:设E(m,6),则AE=m,AO=6.∴,,∴.设直线解析式为,则,,∴直线解析式为.故选A. 10. D 提示:易知直线过定点C(0,-1),可求得直线AB解析式为,直线BC解析式为.将直线绕点C旋转,当直线与直线AB平行时,;当直线过点B时,.∴的取值范围为.故选D.
填空题:11. 提示:由题意得, ,. 12.2或 提示:若4是斜边,则斜边上的中线长为:;若4是直角边,则斜边长为:,则斜边上的中线长为:. 13. 3 提示:由A(-4,2)、B(2,4)可求得直线AB的解析式为,∵点C(m,n)在直线AB上,..与互为倒数,.. 14. 提示:由解得,.,.解得.
5或 提示:当点A翻折到BC边的中点D处时(如图1),AE=DE,∴DE+EC=AE+EC=AC=3,CD=,∴△CDE周长为:DE+EC+CD=3+2=5;当点B翻折到AC边的中点D处时(如图2),BE=DE,∴DE+EC=BE+EC=BC=4,CD=.∴△CDE周长为:DE+EC+CD=.
4 提示:连接CF、BD,由题意可得△ABD≌ACD,∴BD=CD,∠ABD=∠ACD.
当CF⊥AB时,CF取得最小值,这时CF=.∴EF的最小值为4.
解答题
解:.不等式可化为,∴.;
不等式可化为,.,
∵关于的一元一次不等式组的解集为,..
18.(1) (2)答案不唯一
19.解:(1)∵A(3,0)、B(0,4),∴OA=3,OB=4.由折叠可知,,,∴点的坐标为.
(2)设BM=,则..在Rt△中,..解得..
△ABM的面积为:.
解:(1)把代入,得,∴.把代入得,∴.∴.∴点P到轴的距离为.
(2)∵点P落在第二、第四象限的角平分线上,∴可设点P的坐标为.把点分别代入和,得.(2)×3-(1)×2得.解得.∴点P的坐标为(4,-4).
21. (1)证明:如图1,在△ACD和△EBD中,,∴△ACD≌△EBD(SAS).
(2)解:如图2,延长AC到R,使得CR=CA,连接DR.由(1)可知,△ACB≌△RCD,∴AB=DR,∠BAC=∠R.∵AF=EF,∴∠BAC=∠AEF.∵∠AEF=∠DER,∴∠DER=∠R,∴DE=DR=AB.设DE=DR=AB=,则BF=,DF=.由Rt△DBF得,..解得..
22.(1)10,50 (2)当时,;当时,..
(3)在原图上再画出的函数图象(如图1).当时,得,解得.由图1可知①当时,选A方式合算;②当时,选A方式和选B方式一样合算;③当时,选B方式合算.
23.解:(1)当点P在线段AD上运动时(如图①),△APQ是等腰三角形,AQ=2tcm;
(2)如图②,当点E与点C重合时,∵△PQE是等边三角形,∴QE=QP.由(1)得QA=QP,∴AE=2AQ,即6=2×2t.;
①当点P在AD上,点E在AC上时,重合部分是等边三角形PQE,如图③,过点P作PG⊥QE于G,∵∠PAQ=,∴PG=AP=.∴QE=PQ=AQ=2tcm.∴.由(2)知,当E、C重合时,
,.②如图④当点P在AD上,点E在AC延长线上时,重合部分是四边形PQCF.在Rt△FCE中,CE=(4t-6)cm,∠E=,CF=(4t-6)cm..
=().
③当点P在DB上时,重合部分为Rt△PQC,(24).∴关于的函数表达式为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024学年八年级上册数学期末复习提高卷2(浙教版附答案)
一、选择题:(本题共10小题,每小题3分,共30分)
1. 等腰三角形的底边长为16,则腰长的取值可以为( )
A. 6 B. 7 C. 8 D. 9
2. 若关于的方程的解为正实数,则的取值范围是( )
A. B. C. D.
3. 如图,已知点A(2,2).若点P在y轴上,且△APO是等腰三角形,则点P的坐标不可能是( )
A. B. C. (0,-4) D. (0,4)
如图,已知直线与相交于点P,点P的横坐标为-1,则关
于不等式的解在数轴上表示正确的是( )
5.如图,在Rt△ABC中,AB=9,BC=6,∠B=,将△ABC折叠,使A与BC的中点D重合,折痕为MN,则DN的长为( )
A. 4 B. 5 C. 6 D. 7
6. 如图,点D在AC 上,点B在AE上,△ABC≌△DBE,且∠BDA=∠A,∠A:C=5:3.则∠CBE=( )
A. B. C. D.
7.如图所示,△ABC的面积为10,AP垂直于∠ABC的平分线BP于点P,则△PBC的面积为( )
A. B. C. 4 D.
如图,已知点C(1,0),直线与两坐标轴分别交于A、B两点,D、E分别是AB、OA上的动点.则△CDE周长的最小值是( )
B. C. D.
8个边长为2的正方形如图摆放在平面直角坐标系中,经过原点的一条直线将这8个正方形分成面积相等的两部分,则该直线的函数解析式为( )
A. B. C. D.
在平面直角坐标系中,已知A(-1,1)、B(3,3),直线与线段AB的延长线(交点不包括B)相交.则实数的取值范围为( )
B. C. 或 D.
二、填空题:(本题共6小题,每小题3分,共18 分)
11.若点在第二象限,则的取值范围是 .
12. 若一个直角三角形的两条边长分别为3和4,则斜边上的中线长为 .
13. 在平面直角坐标系中,点A(-4,2)、B(2,4)、C(m,n)在同一直线上,若m与n互为倒数,则= .
14. 若方程组的解满足,则的取值范围是 .
15. 已知Rt△ABC中,∠C=90°,AC=3,BC=4,将它的一个锐角翻折,使该锐角顶点落在其对边的中点D处,折痕交另一直角边于点E,交斜边于点F,则△CDE的周长为________.
如图,在等腰△ABC中,AB=AC=8,∠BAC=,AG是底边BC上的高,在AG 的延长线上有一个动点D,连接CD,作∠CDE=,交AB的延长线于点E,∠CDE的角平分线交AB于F.则在点D运动过程中,线段EF的最小值为 .
三、计算题:(本题有8小题,共52分)
17(本题5分).若关于的一元一次不等式组的解集为,求的取值范围.
18(本题7分)在平面直角坐标系中,我们把横、纵坐标都是整数的点称为整点,把顶点都是整点的三角形称为整点三角形.如图,已知整点A(2,2)、B(3,5),请在所给的网格区域(含边界)内按要求画出整点三角形.
在图1中画出以AB为一条直角边的等腰直角三角形ABC;
在图2中画出一个△OBD,使得△OBD的面积等于5,且使点A在△OBD的内部.
19(本题7分)如图,直线AB与轴、y轴分别相较于点、B(0,4),M是OB上一点,若将△ABM沿AM折叠,则点B恰好落在轴上的点处,求:
点的坐标;
△ABM的面积.
20(本题7分)在平面直角坐标系中有点,实数满足以下两个等式:,.
当时,求点P到轴的距离;
若点P落在第二、第四象限的角平分线上,求点P的坐标.
21(本小题7分).在解答几何题目时,常常用到“中线倍长法”.
(1)证明体验:如图1,在△ABC中,AD为BC边上的中线,延长AD至E,使DE=AD,连接BE. 求证:△ACD≌△EBD.
(2)迁移应用:如图2,在△ABD中,∠ABD=,C是BD的中点,F是AB边上一点,连接FD交AC于点E.若AF=EF=3,BD=9. 求DE的长.
22(本小题9分).随着信息技术的快速发展,网上在线学习已渗透到我们日常生活的各个领域.现有某教学网站策划了A、B两种上网学习的月收费方式:
收费方式 月使用费(元) 包时学习时间(h) 超时费(元/min)
A 7 25 0.01
B m n 0.01
设每月上网学习时间为,方案A、B的收费金额分别为、.
如图是与之间的函数关系的图象,请根据图象填空: ,n= .
求与之间的函数表达式.
选择哪种方式上网学习合算,为什么?
23(本小题10分).如图,在△ABC中,∠C=,∠B=,AC=6cm,AD是△ABC的角平分线.动点P从点A出发,以2cm/s的速度沿折线A-D-B向终点B运动.过点P作PQ//AB,交AC于Q.以PQ为边作等边三角形PQE,且点C、E在PQ的同侧.设点P的运动时间为ts(t>0),△PQE与△ABC重合部分的图形面积为.
(1)当点P在线段AD上运动时,判断△APQ的形状(不必证明),并直接写出AQ的长(用含t的代数式表示);
(2)当点E与点C重合时,求t的值;
(3)求S关于t的函数表达式,并写出自变量t的取值范围.
参考答案
选择题:1. D 提示:设腰长为,则,.故选D 2. D 提示:,,,.由题意可知,,.故选D. 3. C 提示:对于选项C:作AM⊥轴于M,若点P坐标为(0,-4),则OP=4..而.又∠AOP>,∴AP为△AOP的最大边,∴AP>OP>OA.∴△APO不是等腰三角形,故选C. 4. C 提示:∵当时,,∴不等式的解集为.故选C. 5. B 提示:设DN=,由对折可知AN=DN=.∵AB=9,∴BN=9.∵BC=6,D为BC的中点,∴BD=3.∵∠B=,,,解得.∴DN=5,故选B. 6. A 提示:由∠A:∠C=5:3可设∠A=,∠C=3,∵∠BDA=∠A,∴∠BDA=5.∵△ABC≌△DBE,∴∠E=∠C=,∠BDE=∠A=.∴∠ADE=∠BDA+∠BDE=.∵∠A+∠ADE+∠E=,,.∴∠CBE=∠A+∠C=.故选A. 7.D 提示:延长AP交BC于M,则△ABP≌△MBP,∴AP=MP.∴,.
.故选D.
8.B 提示:作点C关于直线的对称点M,作点C关于y轴的对称点N,则M(6,5)、N(-1,0).设直线MN交y轴于E,交直线于D,此时△CDE取得最小值.此时,△CDE周长=CD+CE+DE=MD+NE+DE=MN=.故选B.
9. A 提示:设E(m,6),则AE=m,AO=6.∴,,∴.设直线解析式为,则,,∴直线解析式为.故选A. 10. D 提示:易知直线过定点C(0,-1),可求得直线AB解析式为,直线BC解析式为.将直线绕点C旋转,当直线与直线AB平行时,;当直线过点B时,.∴的取值范围为.故选D.
填空题:11. 提示:由题意得, ,. 12.2或 提示:若4是斜边,则斜边上的中线长为:;若4是直角边,则斜边长为:,则斜边上的中线长为:. 13. 3 提示:由A(-4,2)、B(2,4)可求得直线AB的解析式为,∵点C(m,n)在直线AB上,..与互为倒数,.. 14. 提示:由解得,.,.解得.
5或 提示:当点A翻折到BC边的中点D处时(如图1),AE=DE,∴DE+EC=AE+EC=AC=3,CD=,∴△CDE周长为:DE+EC+CD=3+2=5;当点B翻折到AC边的中点D处时(如图2),BE=DE,∴DE+EC=BE+EC=BC=4,CD=.∴△CDE周长为:DE+EC+CD=.
4 提示:连接CF、BD,由题意可得△ABD≌ACD,∴BD=CD,∠ABD=∠ACD.
当CF⊥AB时,CF取得最小值,这时CF=.∴EF的最小值为4.
解答题
解:.不等式可化为,∴.;
不等式可化为,.,
∵关于的一元一次不等式组的解集为,..
18.(1) (2)答案不唯一
19.解:(1)∵A(3,0)、B(0,4),∴OA=3,OB=4.由折叠可知,,,∴点的坐标为.
(2)设BM=,则..在Rt△中,..解得..
△ABM的面积为:.
解:(1)把代入,得,∴.把代入得,∴.∴.∴点P到轴的距离为.
(2)∵点P落在第二、第四象限的角平分线上,∴可设点P的坐标为.把点分别代入和,得.(2)×3-(1)×2得.解得.∴点P的坐标为(4,-4).
21. (1)证明:如图1,在△ACD和△EBD中,,∴△ACD≌△EBD(SAS).
(2)解:如图2,延长AC到R,使得CR=CA,连接DR.由(1)可知,△ACB≌△RCD,∴AB=DR,∠BAC=∠R.∵AF=EF,∴∠BAC=∠AEF.∵∠AEF=∠DER,∴∠DER=∠R,∴DE=DR=AB.设DE=DR=AB=,则BF=,DF=.由Rt△DBF得,..解得..
22.(1)10,50 (2)当时,;当时,..
(3)在原图上再画出的函数图象(如图1).当时,得,解得.由图1可知①当时,选A方式合算;②当时,选A方式和选B方式一样合算;③当时,选B方式合算.
23.解:(1)当点P在线段AD上运动时(如图①),△APQ是等腰三角形,AQ=2tcm;
(2)如图②,当点E与点C重合时,∵△PQE是等边三角形,∴QE=QP.由(1)得QA=QP,∴AE=2AQ,即6=2×2t.;
①当点P在AD上,点E在AC上时,重合部分是等边三角形PQE,如图③,过点P作PG⊥QE于G,∵∠PAQ=,∴PG=AP=.∴QE=PQ=AQ=2tcm.∴.由(2)知,当E、C重合时,
,.②如图④当点P在AD上,点E在AC延长线上时,重合部分是四边形PQCF.在Rt△FCE中,CE=(4t-6)cm,∠E=,CF=(4t-6)cm..
=().
③当点P在DB上时,重合部分为Rt△PQC,(24).∴关于的函数表达式为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
