27.2.2 相似三角形的性质 课件(共23张PPT) 人教版数学九年级下册
文档属性
| 名称 | 27.2.2 相似三角形的性质 课件(共23张PPT) 人教版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 829.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-06 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
27.2.2 相似三角形的性质
理解相似三角形对应高、对应中线、对应角平分线的比等于相似比.
掌握相似三角形周长的比等于相似比,面积的比等于相似比的平方.
能够运用相似三角形性质进行简单的计算与证明.
经历相似三角形性质的探索过程,体会从特殊到一般、类比等数学思想方法.
1
2
3
4
重点:熟练运用相似三角形的性质解决简单的数学问题.
难点:在复杂的几何图形中,准确识别相似三角形,并巧妙运用其性质解决问题.
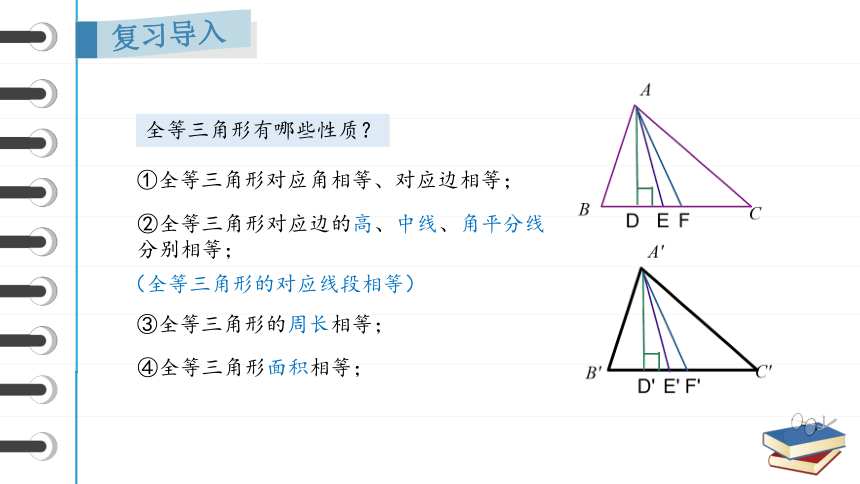
全等三角形有哪些性质?
①全等三角形对应角相等、对应边相等;
②全等三角形对应边的高、中线、角平分线分别相等;
(全等三角形的对应线段相等)
③全等三角形的周长相等;
④全等三角形面积相等;
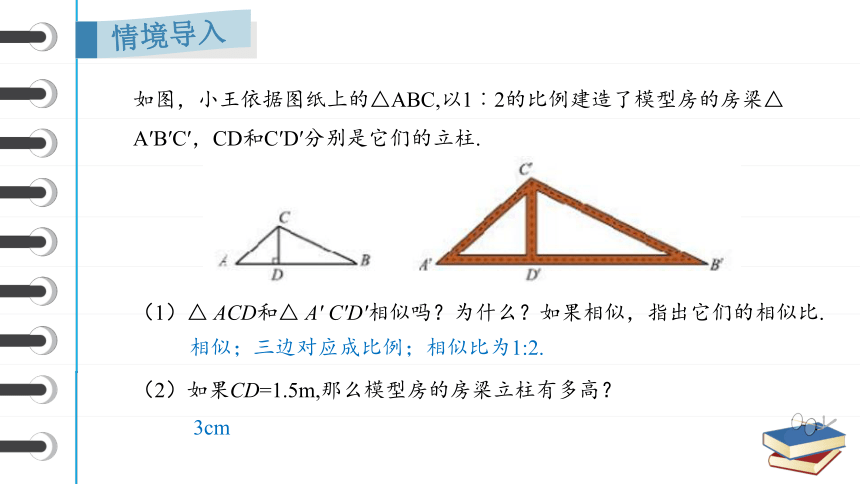
如图,小王依据图纸上的△ABC,以1︰2的比例建造了模型房的房梁△ A′B′C′,CD和C′D′分别是它们的立柱.
(1)△ ACD和△ A′ C′D′相似吗?为什么?如果相似,指出它们的相似比.
(2)如果CD=1.5m,那么模型房的房梁立柱有多高?
相似;三边对应成比例;相似比为1:2.
3cm
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
知识点一:相似三角形对应线段的比
∴△ABD ∽ △A' B' D'
∴
解:如图,分别作出 △ABC 和△A' B' C' 的高 AD 和 A'D'
则∠ADB =∠A' D' B' = 90°
∵△ABC ∽ △A′B′C′
∴∠B =∠B'
A
B
A'
B'
D'
D
C'
C
两角对应相等的两个三角形相似
结论:相似三角形对应高的比等于相似比
解:如图,分别作出 △ABC 和△A' B' C' 的角平分线
AD 和 A'D',则∠BAD =∠B' A' D'
∵△ABC ∽△A′B′C′
∴∠B=∠B' ,
∴△ABD ∽△A' B' D'
∴
两角对应相等的两个三角形相似
结论:相似三角形对应角平分线的比等于相似比
A
B
C
D
A'
B'
C'
D'
解:如图,分别作出 △ABC 和△ A′B′C′的中线 AD 和 A'D',
则
∵△ABC ∽△A′B′C′
∴∠B =∠B' ,
∴△ABD ∽△A' B' D'
∴
两边成比例且夹角相等的两个三角形相似
结论:相似三角形对应中线的比等于相似比
A
B
C
A'
B'
C'
D'
D
A'
B'
A
B
C
D'
D
F
F'
E
E'
符号语言
相似三角形对应高的比,对应角平分线的比,对应中线的比都相等,且都等于相似比.
∵△ABC∽△ A′B′C′ ,相似比是 k
且 AD、A′D′是对应边的高线,
应BF、B′F′是对应边的中线,
CE、C′E′是对角的角平分线,
∴
C'
要点归纳
1. 如果两个相似三角形的对应角平分线的比为 4 : 7,那么对应高的比是 ,对应边上的中线的比是______.
2. △ABC 与 △DEF 的相似比为2: 3,若 BC 边上的高12 cm,则 EF边上的高 =_______ .
4∶7
4∶7
18 cm
基础练习
相似三角形的周长有什么关系呢?
解:如果 △ABC ∽△A'B'C',相似比为 k,那么
因此
AB = kA'B',BC = kB'C',CA = kC'A',
从而
A
B
C
A'
B'
C'
结论:相似三角形周长的比等于相似比
知识点二:相似三角形周长的比
3.如图,在 ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是( )
A.1∶2 B.1∶3 C.1∶4 D.1∶5
A
基础练习
知识点三:相似三角形面积的比
相似三角形面积的比与相似比有什么关系?
如图,△ABC ∽△A′B′C′,相似比为 k,它们的面积比是多少?
A
B
C
A'
B'
C'
A
B
A'
B'
D'
D
C'
C
由前面的结论,得
结论:相似三角形面积的比等于相似比的平方
作三角形的高
例3.如图,在 △ABC 和 △DEF 中,AB = 2DE ,AC = 2DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
A
B
C
D
E
F
A
B
C
D
E
F
解:在 △ABC 和 △DEF 中,∵ AB = 2DE,AC = 2DF,
又 ∵∠D =∠A,
∴ △DEF ∽ △ABC ,相似比为
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
∴
两边成比例且夹角相等的两个三角形相似
4. 如果一个三角形边长扩大为原来的 3 倍,那么面积扩大为原来的______倍;
5. 如果一个三角形面积扩大为原来的 64 倍,那么边长扩大为原来的______倍.
9
8
基础练习
相似三角形的性质
对应线段
周长
面积
等于相似比
对应高的比
对应中线的比
对应角平分线的比
周长的比等于相似比
面积的比等于相似比的平方
1.如图,D是△ABC中AB边上的一点,过点D作DE∥BC交AC于E,已知AD:DB=2:3,则
=( )
A.2:3 B.4:9 C.4:5 D.4:25
D
2.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D.则△BCD与△ABC的周长之比为( ).
A.2∶1 B.1∶2 C.1∶ D. ∶2
B
查漏补缺
3.两个相似三角形的对应边上的高之比是3:5,,周长之和是136,那么这俩个三角形的周长分别是多少?
解:∵两个相似三角形的对应边上的高之比是3 :5,
∴这两个三角形周长比为:3:5.
又∵周长之和是136
∴这两个三角形周长分别为:,.
查漏补缺
4.如图,在△ABC中,点D是AB上一点,且∠A=∠BCD,
,CD=4,则AC长为多少?
解:∵S△ADC:S△CBD=5:4,
∴S△CDB:S△ACB=4:9,
∵∠A=∠BCD,∠ABC=∠CBD,
∴△ABC∽△CBD,
∴
∴
∴AC=6
提升能力
5. 如图,AB∥CD,AO∶AD=2∶5.若△AOB的周长为12,求△COD的周长.
解:∵AB∥CD,∴△AOB∽△DOC,
∴.
∵,∴,
∴,
故△COD的周长为18.
提升能力
27.2.2 相似三角形的性质
理解相似三角形对应高、对应中线、对应角平分线的比等于相似比.
掌握相似三角形周长的比等于相似比,面积的比等于相似比的平方.
能够运用相似三角形性质进行简单的计算与证明.
经历相似三角形性质的探索过程,体会从特殊到一般、类比等数学思想方法.
1
2
3
4
重点:熟练运用相似三角形的性质解决简单的数学问题.
难点:在复杂的几何图形中,准确识别相似三角形,并巧妙运用其性质解决问题.
全等三角形有哪些性质?
①全等三角形对应角相等、对应边相等;
②全等三角形对应边的高、中线、角平分线分别相等;
(全等三角形的对应线段相等)
③全等三角形的周长相等;
④全等三角形面积相等;
如图,小王依据图纸上的△ABC,以1︰2的比例建造了模型房的房梁△ A′B′C′,CD和C′D′分别是它们的立柱.
(1)△ ACD和△ A′ C′D′相似吗?为什么?如果相似,指出它们的相似比.
(2)如果CD=1.5m,那么模型房的房梁立柱有多高?
相似;三边对应成比例;相似比为1:2.
3cm
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
知识点一:相似三角形对应线段的比
∴△ABD ∽ △A' B' D'
∴
解:如图,分别作出 △ABC 和△A' B' C' 的高 AD 和 A'D'
则∠ADB =∠A' D' B' = 90°
∵△ABC ∽ △A′B′C′
∴∠B =∠B'
A
B
A'
B'
D'
D
C'
C
两角对应相等的两个三角形相似
结论:相似三角形对应高的比等于相似比
解:如图,分别作出 △ABC 和△A' B' C' 的角平分线
AD 和 A'D',则∠BAD =∠B' A' D'
∵△ABC ∽△A′B′C′
∴∠B=∠B' ,
∴△ABD ∽△A' B' D'
∴
两角对应相等的两个三角形相似
结论:相似三角形对应角平分线的比等于相似比
A
B
C
D
A'
B'
C'
D'
解:如图,分别作出 △ABC 和△ A′B′C′的中线 AD 和 A'D',
则
∵△ABC ∽△A′B′C′
∴∠B =∠B' ,
∴△ABD ∽△A' B' D'
∴
两边成比例且夹角相等的两个三角形相似
结论:相似三角形对应中线的比等于相似比
A
B
C
A'
B'
C'
D'
D
A'
B'
A
B
C
D'
D
F
F'
E
E'
符号语言
相似三角形对应高的比,对应角平分线的比,对应中线的比都相等,且都等于相似比.
∵△ABC∽△ A′B′C′ ,相似比是 k
且 AD、A′D′是对应边的高线,
应BF、B′F′是对应边的中线,
CE、C′E′是对角的角平分线,
∴
C'
要点归纳
1. 如果两个相似三角形的对应角平分线的比为 4 : 7,那么对应高的比是 ,对应边上的中线的比是______.
2. △ABC 与 △DEF 的相似比为2: 3,若 BC 边上的高12 cm,则 EF边上的高 =_______ .
4∶7
4∶7
18 cm
基础练习
相似三角形的周长有什么关系呢?
解:如果 △ABC ∽△A'B'C',相似比为 k,那么
因此
AB = kA'B',BC = kB'C',CA = kC'A',
从而
A
B
C
A'
B'
C'
结论:相似三角形周长的比等于相似比
知识点二:相似三角形周长的比
3.如图,在 ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是( )
A.1∶2 B.1∶3 C.1∶4 D.1∶5
A
基础练习
知识点三:相似三角形面积的比
相似三角形面积的比与相似比有什么关系?
如图,△ABC ∽△A′B′C′,相似比为 k,它们的面积比是多少?
A
B
C
A'
B'
C'
A
B
A'
B'
D'
D
C'
C
由前面的结论,得
结论:相似三角形面积的比等于相似比的平方
作三角形的高
例3.如图,在 △ABC 和 △DEF 中,AB = 2DE ,AC = 2DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
A
B
C
D
E
F
A
B
C
D
E
F
解:在 △ABC 和 △DEF 中,∵ AB = 2DE,AC = 2DF,
又 ∵∠D =∠A,
∴ △DEF ∽ △ABC ,相似比为
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
∴
两边成比例且夹角相等的两个三角形相似
4. 如果一个三角形边长扩大为原来的 3 倍,那么面积扩大为原来的______倍;
5. 如果一个三角形面积扩大为原来的 64 倍,那么边长扩大为原来的______倍.
9
8
基础练习
相似三角形的性质
对应线段
周长
面积
等于相似比
对应高的比
对应中线的比
对应角平分线的比
周长的比等于相似比
面积的比等于相似比的平方
1.如图,D是△ABC中AB边上的一点,过点D作DE∥BC交AC于E,已知AD:DB=2:3,则
=( )
A.2:3 B.4:9 C.4:5 D.4:25
D
2.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D.则△BCD与△ABC的周长之比为( ).
A.2∶1 B.1∶2 C.1∶ D. ∶2
B
查漏补缺
3.两个相似三角形的对应边上的高之比是3:5,,周长之和是136,那么这俩个三角形的周长分别是多少?
解:∵两个相似三角形的对应边上的高之比是3 :5,
∴这两个三角形周长比为:3:5.
又∵周长之和是136
∴这两个三角形周长分别为:,.
查漏补缺
4.如图,在△ABC中,点D是AB上一点,且∠A=∠BCD,
,CD=4,则AC长为多少?
解:∵S△ADC:S△CBD=5:4,
∴S△CDB:S△ACB=4:9,
∵∠A=∠BCD,∠ABC=∠CBD,
∴△ABC∽△CBD,
∴
∴
∴AC=6
提升能力
5. 如图,AB∥CD,AO∶AD=2∶5.若△AOB的周长为12,求△COD的周长.
解:∵AB∥CD,∴△AOB∽△DOC,
∴.
∵,∴,
∴,
故△COD的周长为18.
提升能力
