27.3 课时1 位似图形 课件(共24张PPT) 人教版数学九年级下册
文档属性
| 名称 | 27.3 课时1 位似图形 课件(共24张PPT) 人教版数学九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-06 13:02:51 | ||
图片预览







文档简介
(共24张PPT)
27.3 位似
课时1 位似图形
理解位似图形的概念,能准确识别位似图形,清楚位似图形与相似图形的联系与区别.
掌握位似图形的性质,能够运用这些性质,在已知位似中心、相似比及部分图形信息的情况下,绘制位似图形;或者通过已知的位似图形,计算相关线段的长度、角度以及确定位似中心的位置等.
学会运用位似变换的思想解决实际问题,提高数学知识的应用能力和建模能力,能够将实际生活中的图形放大或缩小问题转化为位似图形问题进行处理.
1
2
3
重点:理解位似图形的概念,掌握位似图形的性质及画法
难点:准确判断两个图形是否为位似图形,并能够利用位似将一个图
形按一定比例放大或缩小
下面两幅图中的图形都是相似图形吗?它们还有什么特征?
它们对应顶点所在的直线相交于一点
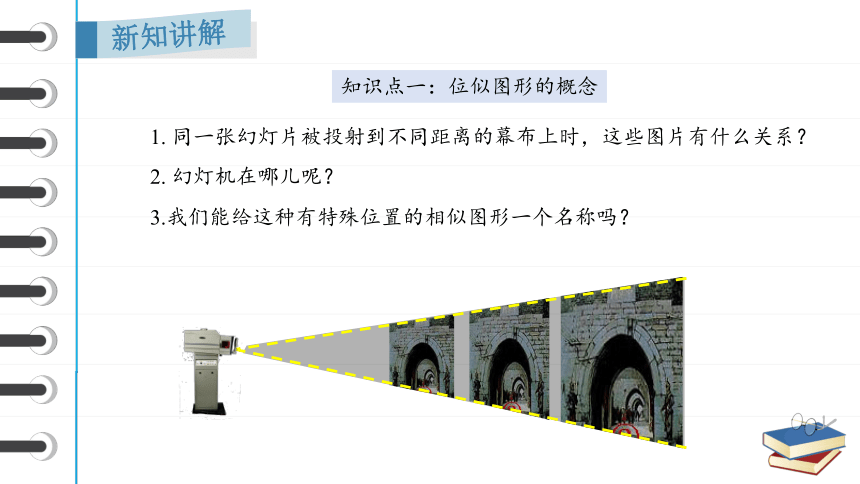
1. 同一张幻灯片被投射到不同距离的幕布上时,这些图片有什么关系?
2. 幻灯机在哪儿呢?
3.我们能给这种有特殊位置的相似图形一个名称吗?
知识点一:位似图形的概念
A
B
C
A1
B1
C1
O
O
A1
B1
C1
D1
E1
A
B
C
D
E
O
A
B
C
D
A1
B1
C1
D1
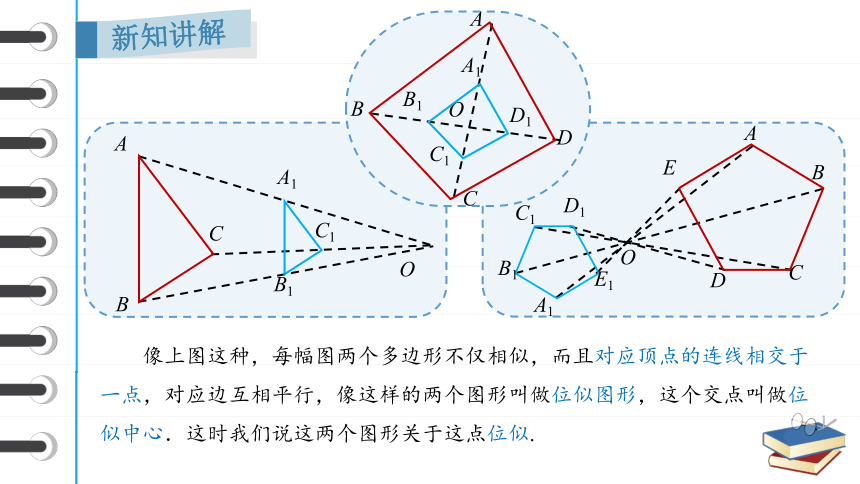
下列图形中有相似多边形吗?如果有,这种相似有什么特征?
像上图这种,每幅图两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,像这样的两个图形叫做位似图形,这个交点叫做位似中心.这时我们说这两个图形关于这点位似.
A
B
C
A1
B1
C1
O
O
A1
B1
C1
D1
E1
A
B
C
D
E
O
A
B
C
D
A1
B1
C1
D1
说明:1.两个位似图形的位似中心有且只有一个.
2.位似中心可能位于两个位似图形的同侧,可能位于两个位似图形之间,也可能位于两个位似图形的内部或边上,还可以是顶点,如图所示.
位似与相似的区别与联系
1.相似只要求两个图形的形状完全相同,而位似不仅要求图形相似,还必须有特殊的位置关系,即对应顶点的连线相交于同一点.
2.如果两个图形是位似图形,那么这两个图形必是相似图形,但相似的两个图形不一定是位似图形.
怎样判断一组图形是否为位似图形?
思考:
对于两个多边形,如果它们的对应顶点的连线相交于一点,并且这点与对应顶点所连线段成比例,那么这两个多边形就是位似多边形.
小技巧:
位似图形对应线段平行或者在一条直线上.
1.判断下列图形(实线部分)是否为位似图形,并在横线处填空.(填“是”或“否”)
______ ______ ______ ______
是
是
否
是
基础练习
观察下列位似图形,运用相似知识思考下列问题
1.两个图形的边角有什么性质?
2.对应点到位似中心的比与相似比有什么关系?
3.你还发现了什么性质?
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
A'
B'
C'
D'
知识点二:位似图形的性质
1. 位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等.
2. 位似图形上任意一对对应点到位似中心的距离之比等于相似比.(位似图形的相似比也叫做位似比)
3. 对应线段平行或者在一条直线上.
位似的性质:
要点归纳
探究
画位似图形
例 把四边形 ABCD 缩小到原来的 .
①在四边形外任选一点 O (如图);
O
D
A
B
C
A'
B'
C'
D'
②连接OA、OB、OC、OD,分别在线段 OA、OB、OC、OD 上取点 A' 、B' 、C' 、D' ,使得 ;
O
D
A
B
C
③顺次连接点 A' 、B' 、C' 、D' ,所得四边形 A'B'C'D' 就是所要求的图形.
利用位似,可以将一个图形放大或缩小
A'
B'
C'
D'
O
D
A
B
C
对于上面的问题,还有其他方法吗?
(1)如果在四边形外任选一个点 O,分别在 OA、OB、OC、OD的反向延长线上取 A′ 、B′ 、C′、D′,使得 呢
两图形在位似中心的两侧
1.在四边形ABCD外任取一点O;
4.顺次连接A′,B′,C′,D′,
所得四边形A′B′C′D′就是所求图形.
2.过点O分别作射线OA,OB,OC,OD;
3.分别在射线OA,OB,OC,OD
的反向延长线上取点A′,B′,C′,D′,
使得
O
D
A
B
C
A'
B'
C'
D'
(2)如果点 O 取在四边形 ABCD 内部呢?
新图形在内部时,可以使图形缩小;新图形在外部时,可以使图形扩大
1.在四边形ABCD内任取一点O;
4.顺次连接A′,B′,C′,D′,
所得四边形A′B′C′D′就是所求图形.
2.过点O分别作射线OA,OB,OC,OD;
3.分别在射线OA,OB,OC,OD
上取点A′,B′,C′,D′,使得
O
D
A
B
C
B'
A'
C'
D'
① 确定位似中心;
② 分别连接并延长位似中心和能代表原图的关键点;
③ 根据相似比,确定能代表所作的位似图形的关键点;
④ 顺次连接上述各点,得到放大或缩小的图形.
画位似图形的一般步骤:
要点归纳
2.如图,以 O 为位似中心,将 △ABC 放大为原来的3 倍.
O
A
B
C
解:①作射线 OA、OB、OC;
②分别在 OA、OB、OC 上取点 A'、B'、C',使得
③顺次连接 A'、B'、C' 就是所要求作的图形.
A'
B'
C'
基础练习
两个相似多边形,如果它们对应顶点的连线相交于一点,我们就把这样的两个图形叫做位似图形,这个交点叫做位似中心
位似图形
概念
位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等
位似图形上任意一对对应点到位似中心的距离之比等于相似比.(位似图形的相似比也叫做位似比)
对应线段平行或者在一条直线上
性质
1.指出下列图形,哪些是位似图形,哪些不是位似图形.
是位似图形
O
O
是位似图形
不是位似图形
查漏补缺
2.(2023吉林长春)如图,△ABC和△A′B′C′是以点O为位似中心的位似图形,点A在线段OA′上.若OA∶AA′=1∶2,则 △ABC与△A′B′C′的相似比为________.
1:3
【解析】∵OA∶AA′=1∶2,
∴OA∶OA′=1∶3,
∴△ABC和△A′B′C′的相似比为1∶3.
查漏补缺
3.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1 : 3,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( ).
A.(3,2) B.(3,1) C.(2,2) C.(2,2) D.(4,2)
A
解析:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1 : 3
∴AD=BC=2,
∵AD//BG,∴△OAD∽△ OBG,
∴ 即OA=1,∴OB=3,∴C点坐标为(3,2).
提升能力
27.3 位似
课时1 位似图形
理解位似图形的概念,能准确识别位似图形,清楚位似图形与相似图形的联系与区别.
掌握位似图形的性质,能够运用这些性质,在已知位似中心、相似比及部分图形信息的情况下,绘制位似图形;或者通过已知的位似图形,计算相关线段的长度、角度以及确定位似中心的位置等.
学会运用位似变换的思想解决实际问题,提高数学知识的应用能力和建模能力,能够将实际生活中的图形放大或缩小问题转化为位似图形问题进行处理.
1
2
3
重点:理解位似图形的概念,掌握位似图形的性质及画法
难点:准确判断两个图形是否为位似图形,并能够利用位似将一个图
形按一定比例放大或缩小
下面两幅图中的图形都是相似图形吗?它们还有什么特征?
它们对应顶点所在的直线相交于一点
1. 同一张幻灯片被投射到不同距离的幕布上时,这些图片有什么关系?
2. 幻灯机在哪儿呢?
3.我们能给这种有特殊位置的相似图形一个名称吗?
知识点一:位似图形的概念
A
B
C
A1
B1
C1
O
O
A1
B1
C1
D1
E1
A
B
C
D
E
O
A
B
C
D
A1
B1
C1
D1
下列图形中有相似多边形吗?如果有,这种相似有什么特征?
像上图这种,每幅图两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,像这样的两个图形叫做位似图形,这个交点叫做位似中心.这时我们说这两个图形关于这点位似.
A
B
C
A1
B1
C1
O
O
A1
B1
C1
D1
E1
A
B
C
D
E
O
A
B
C
D
A1
B1
C1
D1
说明:1.两个位似图形的位似中心有且只有一个.
2.位似中心可能位于两个位似图形的同侧,可能位于两个位似图形之间,也可能位于两个位似图形的内部或边上,还可以是顶点,如图所示.
位似与相似的区别与联系
1.相似只要求两个图形的形状完全相同,而位似不仅要求图形相似,还必须有特殊的位置关系,即对应顶点的连线相交于同一点.
2.如果两个图形是位似图形,那么这两个图形必是相似图形,但相似的两个图形不一定是位似图形.
怎样判断一组图形是否为位似图形?
思考:
对于两个多边形,如果它们的对应顶点的连线相交于一点,并且这点与对应顶点所连线段成比例,那么这两个多边形就是位似多边形.
小技巧:
位似图形对应线段平行或者在一条直线上.
1.判断下列图形(实线部分)是否为位似图形,并在横线处填空.(填“是”或“否”)
______ ______ ______ ______
是
是
否
是
基础练习
观察下列位似图形,运用相似知识思考下列问题
1.两个图形的边角有什么性质?
2.对应点到位似中心的比与相似比有什么关系?
3.你还发现了什么性质?
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
A'
B'
C'
D'
知识点二:位似图形的性质
1. 位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等.
2. 位似图形上任意一对对应点到位似中心的距离之比等于相似比.(位似图形的相似比也叫做位似比)
3. 对应线段平行或者在一条直线上.
位似的性质:
要点归纳
探究
画位似图形
例 把四边形 ABCD 缩小到原来的 .
①在四边形外任选一点 O (如图);
O
D
A
B
C
A'
B'
C'
D'
②连接OA、OB、OC、OD,分别在线段 OA、OB、OC、OD 上取点 A' 、B' 、C' 、D' ,使得 ;
O
D
A
B
C
③顺次连接点 A' 、B' 、C' 、D' ,所得四边形 A'B'C'D' 就是所要求的图形.
利用位似,可以将一个图形放大或缩小
A'
B'
C'
D'
O
D
A
B
C
对于上面的问题,还有其他方法吗?
(1)如果在四边形外任选一个点 O,分别在 OA、OB、OC、OD的反向延长线上取 A′ 、B′ 、C′、D′,使得 呢
两图形在位似中心的两侧
1.在四边形ABCD外任取一点O;
4.顺次连接A′,B′,C′,D′,
所得四边形A′B′C′D′就是所求图形.
2.过点O分别作射线OA,OB,OC,OD;
3.分别在射线OA,OB,OC,OD
的反向延长线上取点A′,B′,C′,D′,
使得
O
D
A
B
C
A'
B'
C'
D'
(2)如果点 O 取在四边形 ABCD 内部呢?
新图形在内部时,可以使图形缩小;新图形在外部时,可以使图形扩大
1.在四边形ABCD内任取一点O;
4.顺次连接A′,B′,C′,D′,
所得四边形A′B′C′D′就是所求图形.
2.过点O分别作射线OA,OB,OC,OD;
3.分别在射线OA,OB,OC,OD
上取点A′,B′,C′,D′,使得
O
D
A
B
C
B'
A'
C'
D'
① 确定位似中心;
② 分别连接并延长位似中心和能代表原图的关键点;
③ 根据相似比,确定能代表所作的位似图形的关键点;
④ 顺次连接上述各点,得到放大或缩小的图形.
画位似图形的一般步骤:
要点归纳
2.如图,以 O 为位似中心,将 △ABC 放大为原来的3 倍.
O
A
B
C
解:①作射线 OA、OB、OC;
②分别在 OA、OB、OC 上取点 A'、B'、C',使得
③顺次连接 A'、B'、C' 就是所要求作的图形.
A'
B'
C'
基础练习
两个相似多边形,如果它们对应顶点的连线相交于一点,我们就把这样的两个图形叫做位似图形,这个交点叫做位似中心
位似图形
概念
位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等
位似图形上任意一对对应点到位似中心的距离之比等于相似比.(位似图形的相似比也叫做位似比)
对应线段平行或者在一条直线上
性质
1.指出下列图形,哪些是位似图形,哪些不是位似图形.
是位似图形
O
O
是位似图形
不是位似图形
查漏补缺
2.(2023吉林长春)如图,△ABC和△A′B′C′是以点O为位似中心的位似图形,点A在线段OA′上.若OA∶AA′=1∶2,则 △ABC与△A′B′C′的相似比为________.
1:3
【解析】∵OA∶AA′=1∶2,
∴OA∶OA′=1∶3,
∴△ABC和△A′B′C′的相似比为1∶3.
查漏补缺
3.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1 : 3,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( ).
A.(3,2) B.(3,1) C.(2,2) C.(2,2) D.(4,2)
A
解析:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1 : 3
∴AD=BC=2,
∵AD//BG,∴△OAD∽△ OBG,
∴ 即OA=1,∴OB=3,∴C点坐标为(3,2).
提升能力
