27.1 图形的相似 课件(共31张PPT) 人教版数学九年级下册
文档属性
| 名称 | 27.1 图形的相似 课件(共31张PPT) 人教版数学九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-06 13:04:38 | ||
图片预览






文档简介
(共31张PPT)
27.1 图形的相似
能通过生活之中的实例认识图形的相似,了解相似多边形的相似比.
会根据相似多边形的概念识别两个多边形是否相似,并会运用相似多边形的性质进行相关的计算.
了解线段的比和成比例的线段.
在学习相似图形的过程之中,加强对相似图形中对应关系的认识,进一步提高数学的推理能力.
1
2
3
4
【重点】理解相似图形的概念,能识别相似图形与相似多边形,准确说出相似多边形的对应角相等、对应边成比例等性质.
【难点】掌握相似比的概念,能依据相似多边形的性质进行相关计算.
全等图形
能够完全重合的两个图形,即它们的形状和大小完全相同.
相同点:形状相同
不同点:大小不相同
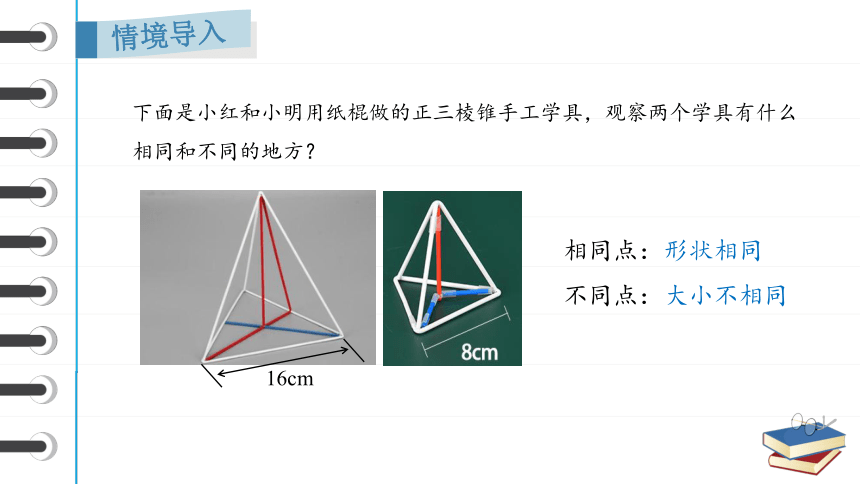
下面是小红和小明用纸棍做的正三棱锥手工学具,观察两个学具有什么相同和不同的地方?
16cm
我们能发现以下学具之间形状相同大小不同,于是我们把这类形状相同大小不同图形叫做相似图形.
相似图形大小一定不同吗?
知识一:相似图形的概念
16cm
全等形和相似图形有什么关系呢?
相似图形
全等形
当两个图形的形状相同、大小也相同时,它们是全等图形,全等图形是相似图形的特殊情况,即全等图形一定是相似图形,但相似图形不一定是全等图形,只有相似图形的大小相同时,它们才全等.
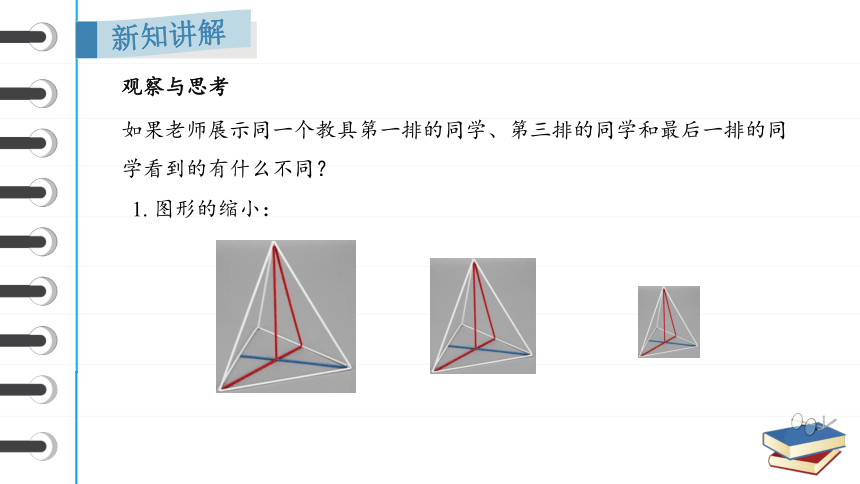
1. 图形的缩小:
如果老师展示同一个教具第一排的同学、第三排的同学和最后一排的同学看到的有什么不同?
观察与思考
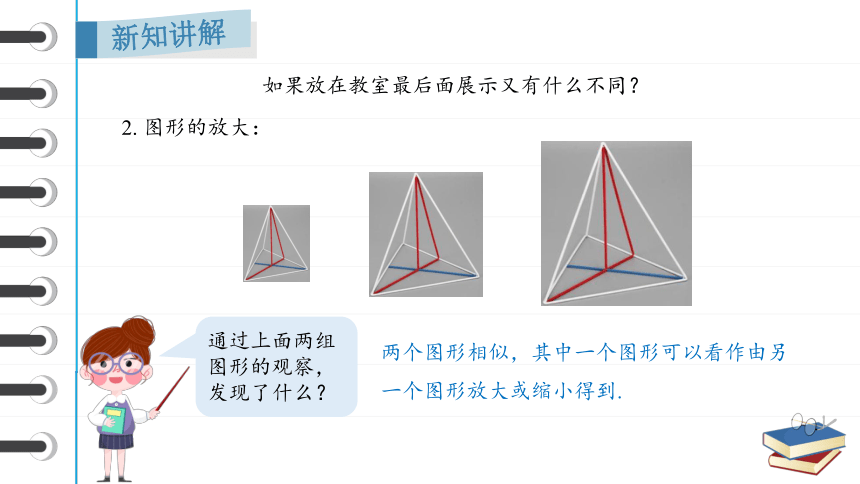
2. 图形的放大:
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
通过上面两组图形的观察,发现了什么?
如果放在教室最后面展示又有什么不同?
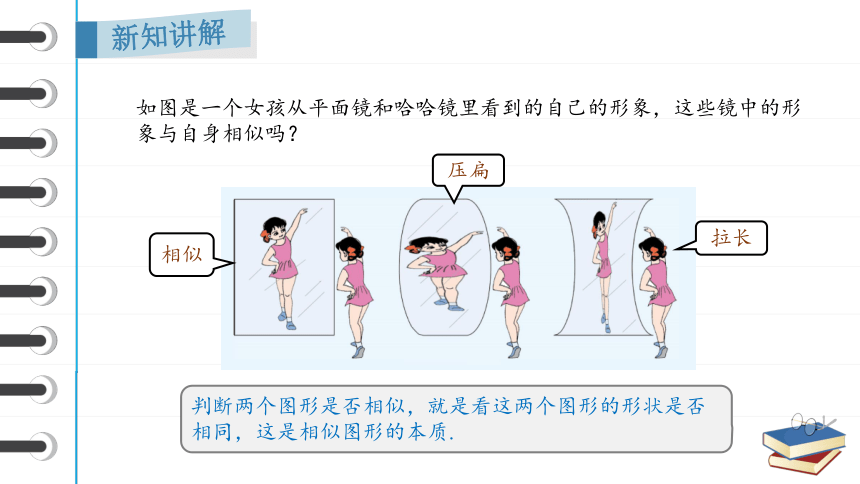
如图是一个女孩从平面镜和哈哈镜里看到的自己的形象,这些镜中的形象与自身相似吗?
判断两个图形是否相似,就是看这两个图形的形状是否相同,这是相似图形的本质.
相似
压扁
拉长
1.“形状相同”是判定相似图形的唯一条件.
2.两个图形相似是指它们的形状相同,与它们的位置、大小无关.
3.全等图形是一种特殊的相似图形,不仅形状相同,大小也相同.
归纳总结
要点归纳
如图,从放大镜里看到的三角尺和原来的三角尺相似吗
相似
基础练习
量一量小红和小明做的正三棱锥手工学具上这四条线段的长度和它们之间的比,你发现了什么?
a
c
b
d
观察与思考
知识二:比例线段
对于四条线段a、b、c、d,如果其中两条线段的比(即它们的长度的比)与另两条线段的比相等,如 (即 ad = bc),我们就说这四条线段成比例.
线段的比:在同一长度单位下,量得的两条线段长度的比叫做这两条线段的比.
注意:线段的比是两条线段的长度比,所以要求两条线段的长度单位必须一致.
a
c
b
d
下列四组长度中的四条线段能成比例的是( )
A. 1 cm,2 cm,2 cm,4 cm
B. 3cm,9 cm,6 cm,8 cm
C. 5 cm,200cm,10 cm,15 cm
D. 6 cm,10 cm,5 cm,20 cm
A
基础练习
1.观察多面体模型与五棱柱教具中的正五边形回答下列问题
观察与思考
知识三:相似多边形与相似比
问题1 这些正五边形两两之间相似吗?
问题2 在这两个正五边形中,是否有对应相等的内角?
问题3 在这两个正五边形中,对应内角的两边是否成比例?
相似
是
是
边数相同,且各角分别相等、各边成比例的两个多边形叫做相似多边形.
相似多边形的对应边的比叫做相似比.
相似多边形的对应角相等,对应边成比例.
相似比:
相似多边形的性质:
相似多边形的定义:
要点归纳
2.下面a1、a2、a3...等边三角形它们相似吗?
a1
a2
a3
an
…
分析:已知等边三角形的每个角都为 60°, 三边都相等. 所以满足边数相同,对应角相等,以及对应边的比相等,即任意两个等边三角形相似.
观察与思考
3
4
甲
5
8
丙
3
6
乙
3.下面甲、乙、丙三个矩形,它们相似吗?
不相似.
因为虽然它们对应角相等,但它们对应边不成比例.
观察与思考
4.下面的菱形都相似吗?为什么?
不一定相似.
因为虽然它们对应边是成比例的,但它们的对应角不一定相等.
观察与思考
5.正方形都相似吗?为什么?所有正多边形呢?
相似,
正方形的每个角都为90°,四边都相等. 所以满足对应角相等,以及对应边的比相等.
任意两个边数相等的正多边形都相似.
观察与思考
①对应角相等
②对应边的比相等,
那么这两个多边形是相似多边形.
相似多边形的判定方法
相似多边形的对应边的比叫作相似比.
要点归纳
例1.如图,四边形 ABCD 和 EFGH 相似,求角 α,β 的大小和 EH 的长度 x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
在四边形 ABCD 中,
β = 360°-(78°+83°+118°) = 81°.
∠α = ∠C = 83°,∠A = ∠E=118°.
解:∵ 四边形 ABCD 和 EFGH 相似,
∴ 它们的对应角相等.由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
∵ 四边形 ABCD 和四边形 EFGH 相似,
∴它们的对应边成比例,由此可得
解得 x = 28 cm.
,即 .
课堂小结
图形的相似
相似图形的概念
四条线段成比例
相似多边形
我们把形状相同的图形叫做相似图形
放大 缩小
两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
相似多边形对应边的比叫做相似比
1.两个相似多边形的相似比是2:3,其中一个多边形的最长边是 6 ,则另一个多边形的最长边是_______.
9或4
分析:不确定所在多边形是较大的还是较小的,所以要分类讨论
解:设另一个多边形最长边为x.
①当x是较大的多边形的边,
,
②当x是较小的多边形的边,
,
∴x=9或4.
查漏补缺
2. 在比例尺为1:10000000的地图上,量的甲、乙两地的距离时30cm,求两地的实际距离.
解:根据题意可得 ∵
∴
∴ 两地的实际距离为
比例尺
在“比例尺、图上距离和实际距离”三个量中,知道任意两个量,便可求出第三个量,但要注意单位的统一
查漏补缺
3.如图所示的两个五边形相似,求未知边 a,b, c,d 的长度.
5
3
2
c
d
7.5
b
a
6
9
解:相似多边形的对应边的成比例,由此可得
解得:a = 3,b = 4.5,c = 4,d = 6.
所以未知边 a,b,c,d 的长度分别为3,4.5,4,6.
, , , ,
提升能力
4.如图,梯形ABCD 与梯形A′B′C′D′相似,AD ∥ BC,A′D′∥ B′C′,
∠ A= ∠ A′,AD=2,A′D′=8,AB=8,B′C′=16,∠ C=60°.
(1)求梯形ABCD 与梯形A′B′C′D′的相似比k;
(2)求A′B′和BC 的长;
(3)求∠ D′的大小.
解:(1)相似比k =
2
8
8
16
提升能力
(2)∵梯形ABCD 与梯形A′B′C′D′相似,且由(1)知相似比k ,
,
∵ AB=8,B′C′=16,∴ A′B′=32,BC=4.
(3)由题意知,∠ D′= ∠ D.
∵ AD ∥ BC,∠ C=60°,
∴∠ D=180°-∠ C=120°,∴∠ D′=120°.
2
8
8
16
27.1 图形的相似
能通过生活之中的实例认识图形的相似,了解相似多边形的相似比.
会根据相似多边形的概念识别两个多边形是否相似,并会运用相似多边形的性质进行相关的计算.
了解线段的比和成比例的线段.
在学习相似图形的过程之中,加强对相似图形中对应关系的认识,进一步提高数学的推理能力.
1
2
3
4
【重点】理解相似图形的概念,能识别相似图形与相似多边形,准确说出相似多边形的对应角相等、对应边成比例等性质.
【难点】掌握相似比的概念,能依据相似多边形的性质进行相关计算.
全等图形
能够完全重合的两个图形,即它们的形状和大小完全相同.
相同点:形状相同
不同点:大小不相同
下面是小红和小明用纸棍做的正三棱锥手工学具,观察两个学具有什么相同和不同的地方?
16cm
我们能发现以下学具之间形状相同大小不同,于是我们把这类形状相同大小不同图形叫做相似图形.
相似图形大小一定不同吗?
知识一:相似图形的概念
16cm
全等形和相似图形有什么关系呢?
相似图形
全等形
当两个图形的形状相同、大小也相同时,它们是全等图形,全等图形是相似图形的特殊情况,即全等图形一定是相似图形,但相似图形不一定是全等图形,只有相似图形的大小相同时,它们才全等.
1. 图形的缩小:
如果老师展示同一个教具第一排的同学、第三排的同学和最后一排的同学看到的有什么不同?
观察与思考
2. 图形的放大:
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
通过上面两组图形的观察,发现了什么?
如果放在教室最后面展示又有什么不同?
如图是一个女孩从平面镜和哈哈镜里看到的自己的形象,这些镜中的形象与自身相似吗?
判断两个图形是否相似,就是看这两个图形的形状是否相同,这是相似图形的本质.
相似
压扁
拉长
1.“形状相同”是判定相似图形的唯一条件.
2.两个图形相似是指它们的形状相同,与它们的位置、大小无关.
3.全等图形是一种特殊的相似图形,不仅形状相同,大小也相同.
归纳总结
要点归纳
如图,从放大镜里看到的三角尺和原来的三角尺相似吗
相似
基础练习
量一量小红和小明做的正三棱锥手工学具上这四条线段的长度和它们之间的比,你发现了什么?
a
c
b
d
观察与思考
知识二:比例线段
对于四条线段a、b、c、d,如果其中两条线段的比(即它们的长度的比)与另两条线段的比相等,如 (即 ad = bc),我们就说这四条线段成比例.
线段的比:在同一长度单位下,量得的两条线段长度的比叫做这两条线段的比.
注意:线段的比是两条线段的长度比,所以要求两条线段的长度单位必须一致.
a
c
b
d
下列四组长度中的四条线段能成比例的是( )
A. 1 cm,2 cm,2 cm,4 cm
B. 3cm,9 cm,6 cm,8 cm
C. 5 cm,200cm,10 cm,15 cm
D. 6 cm,10 cm,5 cm,20 cm
A
基础练习
1.观察多面体模型与五棱柱教具中的正五边形回答下列问题
观察与思考
知识三:相似多边形与相似比
问题1 这些正五边形两两之间相似吗?
问题2 在这两个正五边形中,是否有对应相等的内角?
问题3 在这两个正五边形中,对应内角的两边是否成比例?
相似
是
是
边数相同,且各角分别相等、各边成比例的两个多边形叫做相似多边形.
相似多边形的对应边的比叫做相似比.
相似多边形的对应角相等,对应边成比例.
相似比:
相似多边形的性质:
相似多边形的定义:
要点归纳
2.下面a1、a2、a3...等边三角形它们相似吗?
a1
a2
a3
an
…
分析:已知等边三角形的每个角都为 60°, 三边都相等. 所以满足边数相同,对应角相等,以及对应边的比相等,即任意两个等边三角形相似.
观察与思考
3
4
甲
5
8
丙
3
6
乙
3.下面甲、乙、丙三个矩形,它们相似吗?
不相似.
因为虽然它们对应角相等,但它们对应边不成比例.
观察与思考
4.下面的菱形都相似吗?为什么?
不一定相似.
因为虽然它们对应边是成比例的,但它们的对应角不一定相等.
观察与思考
5.正方形都相似吗?为什么?所有正多边形呢?
相似,
正方形的每个角都为90°,四边都相等. 所以满足对应角相等,以及对应边的比相等.
任意两个边数相等的正多边形都相似.
观察与思考
①对应角相等
②对应边的比相等,
那么这两个多边形是相似多边形.
相似多边形的判定方法
相似多边形的对应边的比叫作相似比.
要点归纳
例1.如图,四边形 ABCD 和 EFGH 相似,求角 α,β 的大小和 EH 的长度 x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
在四边形 ABCD 中,
β = 360°-(78°+83°+118°) = 81°.
∠α = ∠C = 83°,∠A = ∠E=118°.
解:∵ 四边形 ABCD 和 EFGH 相似,
∴ 它们的对应角相等.由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
∵ 四边形 ABCD 和四边形 EFGH 相似,
∴它们的对应边成比例,由此可得
解得 x = 28 cm.
,即 .
课堂小结
图形的相似
相似图形的概念
四条线段成比例
相似多边形
我们把形状相同的图形叫做相似图形
放大 缩小
两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
相似多边形对应边的比叫做相似比
1.两个相似多边形的相似比是2:3,其中一个多边形的最长边是 6 ,则另一个多边形的最长边是_______.
9或4
分析:不确定所在多边形是较大的还是较小的,所以要分类讨论
解:设另一个多边形最长边为x.
①当x是较大的多边形的边,
,
②当x是较小的多边形的边,
,
∴x=9或4.
查漏补缺
2. 在比例尺为1:10000000的地图上,量的甲、乙两地的距离时30cm,求两地的实际距离.
解:根据题意可得 ∵
∴
∴ 两地的实际距离为
比例尺
在“比例尺、图上距离和实际距离”三个量中,知道任意两个量,便可求出第三个量,但要注意单位的统一
查漏补缺
3.如图所示的两个五边形相似,求未知边 a,b, c,d 的长度.
5
3
2
c
d
7.5
b
a
6
9
解:相似多边形的对应边的成比例,由此可得
解得:a = 3,b = 4.5,c = 4,d = 6.
所以未知边 a,b,c,d 的长度分别为3,4.5,4,6.
, , , ,
提升能力
4.如图,梯形ABCD 与梯形A′B′C′D′相似,AD ∥ BC,A′D′∥ B′C′,
∠ A= ∠ A′,AD=2,A′D′=8,AB=8,B′C′=16,∠ C=60°.
(1)求梯形ABCD 与梯形A′B′C′D′的相似比k;
(2)求A′B′和BC 的长;
(3)求∠ D′的大小.
解:(1)相似比k =
2
8
8
16
提升能力
(2)∵梯形ABCD 与梯形A′B′C′D′相似,且由(1)知相似比k ,
,
∵ AB=8,B′C′=16,∴ A′B′=32,BC=4.
(3)由题意知,∠ D′= ∠ D.
∵ AD ∥ BC,∠ C=60°,
∴∠ D=180°-∠ C=120°,∴∠ D′=120°.
2
8
8
16
