27.2.1 课时1 平行线分线段成比例 课件(共27张PPT) 人教版数学九年级下册
文档属性
| 名称 | 27.2.1 课时1 平行线分线段成比例 课件(共27张PPT) 人教版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-06 13:05:18 | ||
图片预览








文档简介
(共27张PPT)
27.2.1 解直角三角形
课时1 平行线分线段成比例
理解相似三角形的概念.
理解平行线分线段成比例的基本事实及其推论,掌握相似三角形判定定理的预备定理的有关证明.
掌握平行线分线段成比例的基本事实及其推论的应用,会用平行线判定两个三角形相似并进行证明和计算.
学会运用类比、转化等数学思想,将平行线分线段成比例问题转化为三角形相似问题,提高分析问题和解决问题的能力.
1
2
3
4
【重点】掌握相似三角形判定定理的预备定理的有关证明.
【难点】能准确识别图形中的对应线段,并能运用定理进行简单的比例计算与线段长度求解
两个边数相同的多边形,如果他们的对应角分别相等,对应边成比例,那么这两个多边形叫相似多边形.
类比
对应角分别相等,并且边也成比例的两个三角形叫作相似三角形
如图,△ABC 和 △A′B′C′ 相似需要满足什么条件?
A
B
C
A′
B′
C′
对应角分别相等,对应边成比例
即∠A=∠A′,∠B=∠B′,∠C=∠C′,
则△ABC与△A′B′C′相似,且相似比为k.
相似用符号“∽”表示,读作“相似于”. △ABC与△A′B′C′ 相似记作△ABC∽△A′B′C′”.
知识点一:相似三角形概念
A
B
C
A′
B′
C′
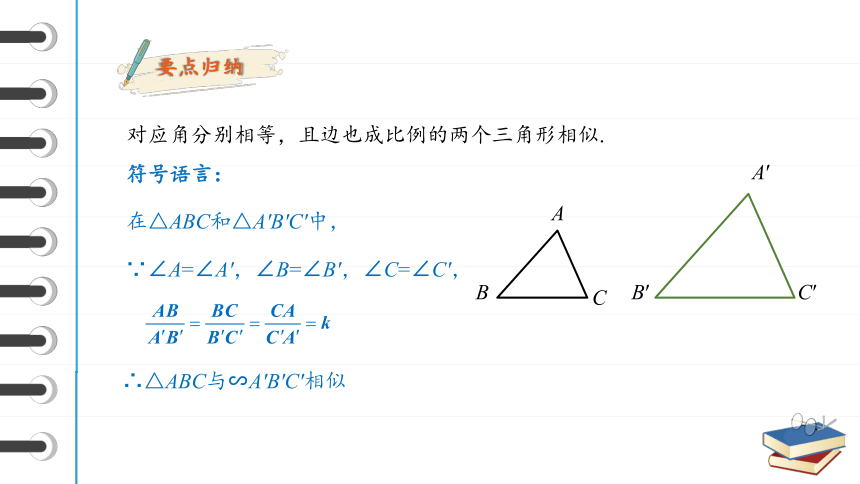
对应角分别相等,且边也成比例的两个三角形相似.
符号语言:
在△ABC和△A'B'C'中,
∵∠A=∠A′,∠B=∠B′,∠C=∠C′,
∴△ABC与∽A′B′C′相似
要点归纳
【注意】
(1)当边的比值等于1时,相似三角形是全等三角形.即相似不一定全等,但全等一定相似.
(2)相似三角形的定义既是最基本的判定方法,也是最本质、最重要的性质.
(3)在书写两三角形相似时,要注意对应点的位置要一致,即△ABC∽△A'B'C',则说明A的对应点是A',B的对应点是B',C的对应点是C'.
要点归纳
思考:△ A'B'C' ∽△ABC与△ABC ∽△ A'B'C'的相似比是否相同?
△ A'B'C' ∽△ABC与△ABC ∽△ A'B'C' 的相似比不同.
注意:相似比带有顺序性,如△ABC∽△ A'B'C' ,
则
反过来△ A'B'C'与△ABC的相似比为
A
B
C
A′
B′
C′
判定三角形全等,我们并不是验证六个条件,而是利用了几个简便的判定定理(SSS,SAS,ASA,AAS),那么判定三角形相似我们又能不能用类似的简便的判定方法呢?我们先来探究下面的问题.
知识点二:平行线分线段成比例(基本事实)及推论
如图,任意画两条直线 l1,l2,再画三条与 l1,l2,都相交的平行线 l3,l4,l5. 分别度量在 l1 上截得的两条线段 AB,BC 和在 l2 上截得的两条线段 DE,EF 的长度
(1) 相等吗?
(2)任意平移 l5, 还相等吗?
A
C
E
B
D
F
l4
l5
l1
l2
l3
通过度量可以发现,若 l3∥ l4 ∥ l5,则 ,
,
任意平移直线 l5 ,
这些线段依然成比例.
A
C
E
B
D
F
l4
l5
l1
l2
l3
注意“对应”两字.
(1) 简称“上比下”等于“上比下”
(2) 简称“上比全”等于“上比全”
(3) 简称“下比全”等于“下比全”
A
C
E
B
D
F
l4
l5
l1
l2
l3
平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
要点归纳
A
B
C
D
E
F
l4
l5
l3
l2
l1
A
B
C
D
E
l4
l5
l3
l2
l1
如图,当直线l1与l2相交时,基本事实还成立吗?
成立. 对应边仍然成比例,即
A
B
C
D
E
l4
l5
l3
l2
l1
成立. 对应边仍然成比例,即
A
B
C
D
E
F
l4
l5
l3
l2
l1
如图,当直线l1与l2相交时,基本事实还成立吗?
把平行线分线段成比例的基本事实应用到三角形中,会出现下面两种情况.
A
B
C
D
E
l4
l5
l3
l2
l1
A
B
C
D
E
l4
l5
l3
l2
l1
平行线分线段成比例定理推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
要点归纳
1.如图,在△ABC中, EF∥BC.
(1) 如果E、F分别是 AB 和 AC 上的点,AE = 2,BE=6,FC= 3,那么 AF 的长是多少?
A
B
C
E
F
解得 AF = 1.
∵EF∥BC,
解:
∴
基础练习
∴
思考:如图,在△ABC中,DE∥BC,且DE分别交AB,AC于点D,E,△ADE与△ABC 有什么关系?
猜测:△ADE∽△ABC
B
C
A
D
E
那么如何去证明它呢?
知识点三:判定三角形相似的引理
我们可以通过相似的定义证明它,即证明∠A=∠A,∠ADE=∠B,∠AED=∠C,
由前面的结论可得,
而除 DE 外,其他的线段都在△ABC 的边上,
要想利用前面学到的结论来证明三角形相似,需将DE平移到BC边上去,使BF=DE,再证明 就可以了.
B
C
A
D
E
证明:先证明两个三角形的角分别相等
在 △ADE与 △ABC中,∠A =∠A.
∵ DE∥BC,∴ ∠ADE =∠B,∠AED =∠C.
如图,过点 E 作 EF∥AB,交 BC 于点 F.
C
B
D
E
F
∵ DE∥BC,EF∥AB,
∴
∵ 四边形DBFE为平行四边形,
∴ DE=BF,
∴△ADE∽△ABC.
∴
再证明两个三角形的边成比例
A
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例
∴
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
定理应用格式:
∵ DE∥BC
∴ △ADE∽△ABC
B
C
A
D
E
三角形相似的两种常见类型:
“A ”型
“X ”型
D
E
A
B
C
A
B
C
D
E
要点归纳
2.问题:如图,DE∥BC,且 DE 分别交 BA,CA 的延长线于点 D,E,△ABC 与△ADE 相似吗?如何证明呢?
基础练习
证明:先证明两个三角形的角分别相等.
如图,在△ADE 与△ABC 中,∠DAE=∠BAC.
∵DE//BC,∴∠D=∠B,∠AED=∠C.
再证明两个三角形的边成比例.
过点E作EF//AB,交CB的延长线于点F.
∵DE//BC,EF//AB,
C
D
B
A
E
F
2.问题:如图,DE∥BC,且 DE 分别交 BA,CA 的延长线于点 D,E,△ABC 与△ADE 相似吗?如何证明呢?
基础练习
C
D
B
A
E
F
∵四边形DBFE是平行四边形,
∴DE=BF.
∴ △ADE和△ABC的角分别相等,边成比例,
∴ △ADE∽△ABC.
两条直线被一组平行线所截,所得的对应线段成比例
推论:
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例
相似三角形判定的引理:
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似
基本事实:
平行线分线段成比例
1.直线AB//CD//EF,若AC=4,CE=11,则 , .
A
C
E
B
D
F
解:∵AB//CD//EF,
∴==,
∵AC=4,CE=11,∴AE=15
∴==.
查漏补缺
2.如图,AB//DE,若AB=9,BC=3,DC=1,则DE=____.
3
A
B
C
D
E
3. 已知:如图,AB∥EF∥CD,图中共有___对相似三角形.
C
D
A
B
E
F
O
3
查漏补缺
3.如图,□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
A.3:2 B.3:1
C.1:1 D.1:2
D
查漏补缺
4.如图,在 □ABCD 中,EF∥CD, BE: BC = 2: 9,EF = 4,求 AB的长.
解:∵ EF∥CD,BE : BC= 2 : 9,
D
A
C
B
E
F
∴ △BEF ∽ △BCD,
解得 CD = 18.
又 ∵ 四边形 ABCD 为平行四边形,
∴ AB=CD =18.
提升能力
∴=,
即=,
27.2.1 解直角三角形
课时1 平行线分线段成比例
理解相似三角形的概念.
理解平行线分线段成比例的基本事实及其推论,掌握相似三角形判定定理的预备定理的有关证明.
掌握平行线分线段成比例的基本事实及其推论的应用,会用平行线判定两个三角形相似并进行证明和计算.
学会运用类比、转化等数学思想,将平行线分线段成比例问题转化为三角形相似问题,提高分析问题和解决问题的能力.
1
2
3
4
【重点】掌握相似三角形判定定理的预备定理的有关证明.
【难点】能准确识别图形中的对应线段,并能运用定理进行简单的比例计算与线段长度求解
两个边数相同的多边形,如果他们的对应角分别相等,对应边成比例,那么这两个多边形叫相似多边形.
类比
对应角分别相等,并且边也成比例的两个三角形叫作相似三角形
如图,△ABC 和 △A′B′C′ 相似需要满足什么条件?
A
B
C
A′
B′
C′
对应角分别相等,对应边成比例
即∠A=∠A′,∠B=∠B′,∠C=∠C′,
则△ABC与△A′B′C′相似,且相似比为k.
相似用符号“∽”表示,读作“相似于”. △ABC与△A′B′C′ 相似记作△ABC∽△A′B′C′”.
知识点一:相似三角形概念
A
B
C
A′
B′
C′
对应角分别相等,且边也成比例的两个三角形相似.
符号语言:
在△ABC和△A'B'C'中,
∵∠A=∠A′,∠B=∠B′,∠C=∠C′,
∴△ABC与∽A′B′C′相似
要点归纳
【注意】
(1)当边的比值等于1时,相似三角形是全等三角形.即相似不一定全等,但全等一定相似.
(2)相似三角形的定义既是最基本的判定方法,也是最本质、最重要的性质.
(3)在书写两三角形相似时,要注意对应点的位置要一致,即△ABC∽△A'B'C',则说明A的对应点是A',B的对应点是B',C的对应点是C'.
要点归纳
思考:△ A'B'C' ∽△ABC与△ABC ∽△ A'B'C'的相似比是否相同?
△ A'B'C' ∽△ABC与△ABC ∽△ A'B'C' 的相似比不同.
注意:相似比带有顺序性,如△ABC∽△ A'B'C' ,
则
反过来△ A'B'C'与△ABC的相似比为
A
B
C
A′
B′
C′
判定三角形全等,我们并不是验证六个条件,而是利用了几个简便的判定定理(SSS,SAS,ASA,AAS),那么判定三角形相似我们又能不能用类似的简便的判定方法呢?我们先来探究下面的问题.
知识点二:平行线分线段成比例(基本事实)及推论
如图,任意画两条直线 l1,l2,再画三条与 l1,l2,都相交的平行线 l3,l4,l5. 分别度量在 l1 上截得的两条线段 AB,BC 和在 l2 上截得的两条线段 DE,EF 的长度
(1) 相等吗?
(2)任意平移 l5, 还相等吗?
A
C
E
B
D
F
l4
l5
l1
l2
l3
通过度量可以发现,若 l3∥ l4 ∥ l5,则 ,
,
任意平移直线 l5 ,
这些线段依然成比例.
A
C
E
B
D
F
l4
l5
l1
l2
l3
注意“对应”两字.
(1) 简称“上比下”等于“上比下”
(2) 简称“上比全”等于“上比全”
(3) 简称“下比全”等于“下比全”
A
C
E
B
D
F
l4
l5
l1
l2
l3
平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
要点归纳
A
B
C
D
E
F
l4
l5
l3
l2
l1
A
B
C
D
E
l4
l5
l3
l2
l1
如图,当直线l1与l2相交时,基本事实还成立吗?
成立. 对应边仍然成比例,即
A
B
C
D
E
l4
l5
l3
l2
l1
成立. 对应边仍然成比例,即
A
B
C
D
E
F
l4
l5
l3
l2
l1
如图,当直线l1与l2相交时,基本事实还成立吗?
把平行线分线段成比例的基本事实应用到三角形中,会出现下面两种情况.
A
B
C
D
E
l4
l5
l3
l2
l1
A
B
C
D
E
l4
l5
l3
l2
l1
平行线分线段成比例定理推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
要点归纳
1.如图,在△ABC中, EF∥BC.
(1) 如果E、F分别是 AB 和 AC 上的点,AE = 2,BE=6,FC= 3,那么 AF 的长是多少?
A
B
C
E
F
解得 AF = 1.
∵EF∥BC,
解:
∴
基础练习
∴
思考:如图,在△ABC中,DE∥BC,且DE分别交AB,AC于点D,E,△ADE与△ABC 有什么关系?
猜测:△ADE∽△ABC
B
C
A
D
E
那么如何去证明它呢?
知识点三:判定三角形相似的引理
我们可以通过相似的定义证明它,即证明∠A=∠A,∠ADE=∠B,∠AED=∠C,
由前面的结论可得,
而除 DE 外,其他的线段都在△ABC 的边上,
要想利用前面学到的结论来证明三角形相似,需将DE平移到BC边上去,使BF=DE,再证明 就可以了.
B
C
A
D
E
证明:先证明两个三角形的角分别相等
在 △ADE与 △ABC中,∠A =∠A.
∵ DE∥BC,∴ ∠ADE =∠B,∠AED =∠C.
如图,过点 E 作 EF∥AB,交 BC 于点 F.
C
B
D
E
F
∵ DE∥BC,EF∥AB,
∴
∵ 四边形DBFE为平行四边形,
∴ DE=BF,
∴△ADE∽△ABC.
∴
再证明两个三角形的边成比例
A
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例
∴
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
定理应用格式:
∵ DE∥BC
∴ △ADE∽△ABC
B
C
A
D
E
三角形相似的两种常见类型:
“A ”型
“X ”型
D
E
A
B
C
A
B
C
D
E
要点归纳
2.问题:如图,DE∥BC,且 DE 分别交 BA,CA 的延长线于点 D,E,△ABC 与△ADE 相似吗?如何证明呢?
基础练习
证明:先证明两个三角形的角分别相等.
如图,在△ADE 与△ABC 中,∠DAE=∠BAC.
∵DE//BC,∴∠D=∠B,∠AED=∠C.
再证明两个三角形的边成比例.
过点E作EF//AB,交CB的延长线于点F.
∵DE//BC,EF//AB,
C
D
B
A
E
F
2.问题:如图,DE∥BC,且 DE 分别交 BA,CA 的延长线于点 D,E,△ABC 与△ADE 相似吗?如何证明呢?
基础练习
C
D
B
A
E
F
∵四边形DBFE是平行四边形,
∴DE=BF.
∴ △ADE和△ABC的角分别相等,边成比例,
∴ △ADE∽△ABC.
两条直线被一组平行线所截,所得的对应线段成比例
推论:
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例
相似三角形判定的引理:
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似
基本事实:
平行线分线段成比例
1.直线AB//CD//EF,若AC=4,CE=11,则 , .
A
C
E
B
D
F
解:∵AB//CD//EF,
∴==,
∵AC=4,CE=11,∴AE=15
∴==.
查漏补缺
2.如图,AB//DE,若AB=9,BC=3,DC=1,则DE=____.
3
A
B
C
D
E
3. 已知:如图,AB∥EF∥CD,图中共有___对相似三角形.
C
D
A
B
E
F
O
3
查漏补缺
3.如图,□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
A.3:2 B.3:1
C.1:1 D.1:2
D
查漏补缺
4.如图,在 □ABCD 中,EF∥CD, BE: BC = 2: 9,EF = 4,求 AB的长.
解:∵ EF∥CD,BE : BC= 2 : 9,
D
A
C
B
E
F
∴ △BEF ∽ △BCD,
解得 CD = 18.
又 ∵ 四边形 ABCD 为平行四边形,
∴ AB=CD =18.
提升能力
∴=,
即=,
