27.2.1 课时3 两角相等判定 课件(共21张PPT) 人教版数学九年级下册
文档属性
| 名称 | 27.2.1 课时3 两角相等判定 课件(共21张PPT) 人教版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 666.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-06 13:07:35 | ||
图片预览







文档简介
(共21张PPT)
27.2.1 相似三角形的判定
课时3 两角相等判定
理解并牢记两角分别相等的两个三角形相似这一判定定理,熟练掌握直角三角形相似的判定方法;能够运用这些判定条件解决相关的证明与计算问题.
通过观察、测量、对比不同三角形的角与边的关系,经历从特殊到一般、从直观感知到理性推导的过程,归纳出相似三角形的判定定理,提升逻辑推理与归纳总结能力.
在利用相似三角形判定定理解决实际问题的过程中,体会数学知识之间的内在联系,学会将复杂问题转化为简单的相似三角形问题进行求解,培养数学思维和应用意识.
1
2
3
重点:理解并掌握两角分别相等的两个三角形相似的判定定理及判定两个直角三角形相似的方法.
难点:灵活应用三角形相似的判定解决数学问题.
目前为止,我们学习了哪些判定三角形相似的方法?
1.定义法:对应角相等,对应边成比例的三角形相似
2.平行线法:平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.
3.三边成比例的两个三角形相似.
4.两边成比例且夹角相等的两个三角形相似.
思考:类似于判定三角形全等的AAS和ASA的方法,你能得到哪些判定三角形相似的方法呢?
观察两副三角尺如图所示,其中有同样两个锐角(30°与60°,或45°与45°)的两个三角尺大小可能不同,但它们看起来是相似的.
知识点一:两角分别相等的两个三角形相似
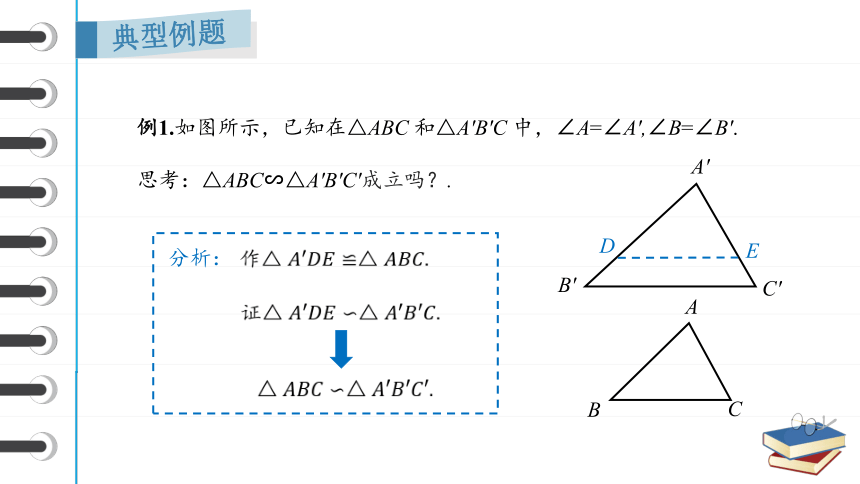
例1.如图所示,已知在△ABC 和△A′B′C 中,∠A=∠A′,∠B=∠B′.
思考:△ABC∽△A′B′C′成立吗?.
分析:
作
证
A
B
C
A'
B'
C'
D
E
A
B
C
A'
B'
C'
D
E
证明:在线段A′B′上截取A′D=AB,过点D作DE∥B′C′,交A′C′于点E,则可得△A′DE∽△A′B′C′.
∵DE∥B′C′,∴∠A′DE=∠B′
又∠B=∠B′,∴∠B=∠A′DE
又∵∠A=∠A′,A′D=AB
∴△A′DE≌△ABC
∴△ABC∽△A′B′C′.
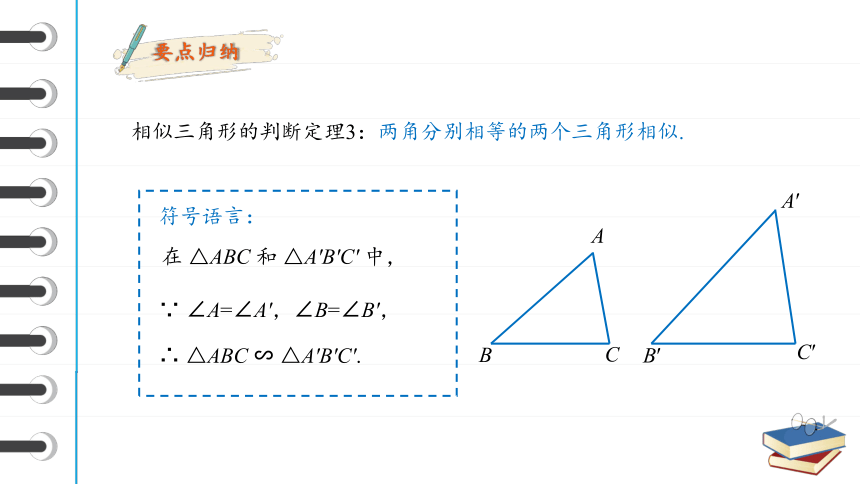
相似三角形的判断定理3:两角分别相等的两个三角形相似.
∵ ∠A=∠A',∠B=∠B',
∴ △ABC ∽ △A'B'C'.
符号语言:
在 △ABC 和 △A'B'C' 中,
A
B
C
A′
C′
B′
要点归纳
证明:∵ 在△ ABC中,∠B=80 °,∠C=60 °,
∴ ∠A=180 °-∠C-∠B=40 °.
∵ 在△DEF中,∠E=80 °,∠D=40 °.
∴ ∠B=∠E,∠A=∠E.
∴ △ABC ∽△DEF.
1. 如图,△ABC 和 △DEF 中,∠B=80°,∠C=60°,∠E=80 °,∠D=40 °求证:△ABC ∽△DEF.
A
C
B
F
E
D
基础练习
例2.如图,Rt△ABC中,∠C=90°,AB=10,AC=8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D.求AD的长.
D
A
B
C
E
解:∵E D⊥AB,∴∠EDA = 90°
又∠C = 90°,∠A =∠A,
∴△AED∽△ABC,
∴
∴
方法总结:由三角形相似的条件可知,如果两个直角三角形满足一个锐角相等,或两组直角边成比例,那么这两个直角三角形相似.
知识点二:判定两个直角三角形相似
如图所示,在 Rt△ABC 和 Rt△A′B′C′中,∠C=90°,∠C′=90°
,求证 Rt△ABC∽Rt△A′B′C′.
C
A
A'
B
B'
C'
分析:要证Rt△ABC∽Rt△A'B'C',
可设法证明
,只需证
若设
证明:设 = k,则 AB = kA′B′,AC = kA′C′.
由勾股定理,得
∴ .
∴ Rt△ABC ∽ Rt△A′B′C′.
∴
C
A
A'
B
B'
C'
斜边和一直角边成比例的两个直角三角形相似.
在 Rt△ABC 和 Rt△A′B′C′ 中,
符号语言:
∵∠C=90°,∠C′=90°
且
∴ △ABC ∽ △A′B′C′ .
C
A
A'
B
B'
C'
要点归纳
2.如图,Rt△ABC中,CD是斜边AB上的高.
求证:(1)△ACD∽△ABC;(2)△CBD∽△ABC.
证明:
(1)∵ CD是斜边AB上的高,
∴ ∠CDA=90°.
∵ ∠ACB=90 °, ∴ ∠CDA=∠ACB.
又∵ ∠A=∠A,∴△ACD∽△ABC.
(2)同理可得∠CDB=∠ACB.
又∵ ∠B=∠B,∴△CBD∽△ABC.
基础练习
三角形相似的判定3
直角三角形相似的判定方法:
(1)有一个锐角相等;
(2)两组直角边对应成比例;
(3)一般的三角形相似的方法;
(4)有一组直角边和斜边对应成比例
判定定理3:
两角分别相等的两个三角形相似
1.如图,下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACB B.∠ADB=∠ABC
C.AB2=AD AC D.
D
查漏补缺
A
B
D
C
2. 如图,点 D 在 AB上,当∠ =∠ (或
∠ =∠ )时,△ACD∽△ABC.
ACD
ACB
B
ADC
3. 在 Rt△ABC 和 Rt△DEF 中,∠C=∠F=90°,
依据下列各组条件判定这两个三角形是否相似.
(1) ∠A=35°,∠E=55°: ;
(2) AC=5,BC=4,DF=10,EF=8: ;
(3) AB=10,AC=8,DE=25,EF=15: .
相似
相似
相似
查漏补缺
4. 如图,在 Rt△ABC 中, ∠ABC = 90°,BD⊥AC于D. 若 AB=8,AD=4,则 BD= ,AC= ,BC= .
16
D
B
C
A
∟
查漏补缺
5.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.
求证:△ABD∽△CBE.
解:∵在△ABC中,AB=AC,BD=CD,
∴AD⊥BC.
又∵CE⊥AB,
∴∠ADB=∠CEB=90°,
又∵∠B=∠B,
∴△ABD∽△CBE.
提升能力
6.如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
解:(1)∵∠C=90°,△ACD沿AD折叠,
∴∠C=∠AED=90°,
∴∠DEB=∠C=90°,
∵∠B=∠B,
∴△BDE∽△BAC;
提升能力
(2)由勾股定理得,AB=10,由折叠的性质知,AE=AC=6,DE=CD,
∴BE=AB﹣AE=10﹣6=4,
∵△BDE∽△BAC,∴,
∴,
∴
在Rt△ACD中,由勾股定理得
即
解得:AD=
27.2.1 相似三角形的判定
课时3 两角相等判定
理解并牢记两角分别相等的两个三角形相似这一判定定理,熟练掌握直角三角形相似的判定方法;能够运用这些判定条件解决相关的证明与计算问题.
通过观察、测量、对比不同三角形的角与边的关系,经历从特殊到一般、从直观感知到理性推导的过程,归纳出相似三角形的判定定理,提升逻辑推理与归纳总结能力.
在利用相似三角形判定定理解决实际问题的过程中,体会数学知识之间的内在联系,学会将复杂问题转化为简单的相似三角形问题进行求解,培养数学思维和应用意识.
1
2
3
重点:理解并掌握两角分别相等的两个三角形相似的判定定理及判定两个直角三角形相似的方法.
难点:灵活应用三角形相似的判定解决数学问题.
目前为止,我们学习了哪些判定三角形相似的方法?
1.定义法:对应角相等,对应边成比例的三角形相似
2.平行线法:平行于三角形一边的直线,截其他两边所得的三角形与原三角形相似.
3.三边成比例的两个三角形相似.
4.两边成比例且夹角相等的两个三角形相似.
思考:类似于判定三角形全等的AAS和ASA的方法,你能得到哪些判定三角形相似的方法呢?
观察两副三角尺如图所示,其中有同样两个锐角(30°与60°,或45°与45°)的两个三角尺大小可能不同,但它们看起来是相似的.
知识点一:两角分别相等的两个三角形相似
例1.如图所示,已知在△ABC 和△A′B′C 中,∠A=∠A′,∠B=∠B′.
思考:△ABC∽△A′B′C′成立吗?.
分析:
作
证
A
B
C
A'
B'
C'
D
E
A
B
C
A'
B'
C'
D
E
证明:在线段A′B′上截取A′D=AB,过点D作DE∥B′C′,交A′C′于点E,则可得△A′DE∽△A′B′C′.
∵DE∥B′C′,∴∠A′DE=∠B′
又∠B=∠B′,∴∠B=∠A′DE
又∵∠A=∠A′,A′D=AB
∴△A′DE≌△ABC
∴△ABC∽△A′B′C′.
相似三角形的判断定理3:两角分别相等的两个三角形相似.
∵ ∠A=∠A',∠B=∠B',
∴ △ABC ∽ △A'B'C'.
符号语言:
在 △ABC 和 △A'B'C' 中,
A
B
C
A′
C′
B′
要点归纳
证明:∵ 在△ ABC中,∠B=80 °,∠C=60 °,
∴ ∠A=180 °-∠C-∠B=40 °.
∵ 在△DEF中,∠E=80 °,∠D=40 °.
∴ ∠B=∠E,∠A=∠E.
∴ △ABC ∽△DEF.
1. 如图,△ABC 和 △DEF 中,∠B=80°,∠C=60°,∠E=80 °,∠D=40 °求证:△ABC ∽△DEF.
A
C
B
F
E
D
基础练习
例2.如图,Rt△ABC中,∠C=90°,AB=10,AC=8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D.求AD的长.
D
A
B
C
E
解:∵E D⊥AB,∴∠EDA = 90°
又∠C = 90°,∠A =∠A,
∴△AED∽△ABC,
∴
∴
方法总结:由三角形相似的条件可知,如果两个直角三角形满足一个锐角相等,或两组直角边成比例,那么这两个直角三角形相似.
知识点二:判定两个直角三角形相似
如图所示,在 Rt△ABC 和 Rt△A′B′C′中,∠C=90°,∠C′=90°
,求证 Rt△ABC∽Rt△A′B′C′.
C
A
A'
B
B'
C'
分析:要证Rt△ABC∽Rt△A'B'C',
可设法证明
,只需证
若设
证明:设 = k,则 AB = kA′B′,AC = kA′C′.
由勾股定理,得
∴ .
∴ Rt△ABC ∽ Rt△A′B′C′.
∴
C
A
A'
B
B'
C'
斜边和一直角边成比例的两个直角三角形相似.
在 Rt△ABC 和 Rt△A′B′C′ 中,
符号语言:
∵∠C=90°,∠C′=90°
且
∴ △ABC ∽ △A′B′C′ .
C
A
A'
B
B'
C'
要点归纳
2.如图,Rt△ABC中,CD是斜边AB上的高.
求证:(1)△ACD∽△ABC;(2)△CBD∽△ABC.
证明:
(1)∵ CD是斜边AB上的高,
∴ ∠CDA=90°.
∵ ∠ACB=90 °, ∴ ∠CDA=∠ACB.
又∵ ∠A=∠A,∴△ACD∽△ABC.
(2)同理可得∠CDB=∠ACB.
又∵ ∠B=∠B,∴△CBD∽△ABC.
基础练习
三角形相似的判定3
直角三角形相似的判定方法:
(1)有一个锐角相等;
(2)两组直角边对应成比例;
(3)一般的三角形相似的方法;
(4)有一组直角边和斜边对应成比例
判定定理3:
两角分别相等的两个三角形相似
1.如图,下列条件不能判定△ADB∽△ABC的是( )
A.∠ABD=∠ACB B.∠ADB=∠ABC
C.AB2=AD AC D.
D
查漏补缺
A
B
D
C
2. 如图,点 D 在 AB上,当∠ =∠ (或
∠ =∠ )时,△ACD∽△ABC.
ACD
ACB
B
ADC
3. 在 Rt△ABC 和 Rt△DEF 中,∠C=∠F=90°,
依据下列各组条件判定这两个三角形是否相似.
(1) ∠A=35°,∠E=55°: ;
(2) AC=5,BC=4,DF=10,EF=8: ;
(3) AB=10,AC=8,DE=25,EF=15: .
相似
相似
相似
查漏补缺
4. 如图,在 Rt△ABC 中, ∠ABC = 90°,BD⊥AC于D. 若 AB=8,AD=4,则 BD= ,AC= ,BC= .
16
D
B
C
A
∟
查漏补缺
5.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.
求证:△ABD∽△CBE.
解:∵在△ABC中,AB=AC,BD=CD,
∴AD⊥BC.
又∵CE⊥AB,
∴∠ADB=∠CEB=90°,
又∵∠B=∠B,
∴△ABD∽△CBE.
提升能力
6.如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
解:(1)∵∠C=90°,△ACD沿AD折叠,
∴∠C=∠AED=90°,
∴∠DEB=∠C=90°,
∵∠B=∠B,
∴△BDE∽△BAC;
提升能力
(2)由勾股定理得,AB=10,由折叠的性质知,AE=AC=6,DE=CD,
∴BE=AB﹣AE=10﹣6=4,
∵△BDE∽△BAC,∴,
∴,
∴
在Rt△ACD中,由勾股定理得
即
解得:AD=
