16.1 课时2 二次根式的双重非负性 课件(共14张PPT) 人教版数学八年级下册
文档属性
| 名称 | 16.1 课时2 二次根式的双重非负性 课件(共14张PPT) 人教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 669.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-06 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
课时2 二次根式的双重非负性
16.1 二次根式
透彻领悟二次根式的双重非负性本质,能够灵活运用该性质进行基础的运算与推理;熟练掌握运用二次根式双重非负性去处理代数式求值、等式成立判定等问题的技巧.
经由对诸多二次根式双重非负性相关例题、习题的深度分析与解答,强化逻辑思维与数学运算这两项核心能力.
当面临利用双重非负性解决较为复杂的问题(如多个非负项累加为零的情形)时,学会有条不紊地综合分析、层层推导的有效思维方式.
深切体会二次根式双重非负性在整个数学体系里的关键作用,强化对数学重要性质的重视程度与运用意识,进而激发对初中数学学习的浓厚兴趣.
1
2
3
4
【重点】透彻领悟二次根式的双重非负性本质.
【难点】灵活运用二次根式的双重非负性进行基础的运算与推理; 熟练掌握代数式求值、等式成立判定等问题的技巧.
二次根式的双重非负性
前者x为全体实数;后者x为正数和0.
当a>0时, 表示a的算术平方根,因此>0;
综上所述:当a≥0时, ≥0.
[问题1]当x是怎样的实数时,在实数范围内有意义? 呢?
[问题2]二次根式的被开方数a的取值范围是什么?它本身的取值范围又是什么?
当a=0时,表示0的算术平方根,因此=0.
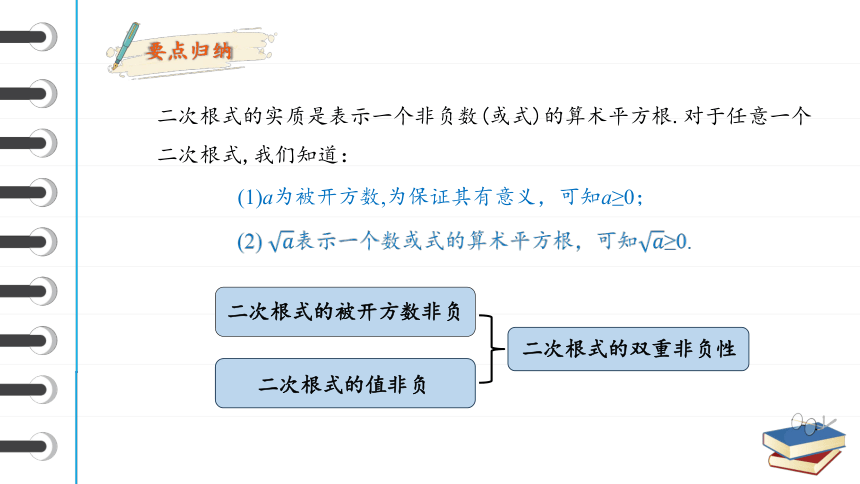
二次根式的实质是表示一个非负数(或式)的算术平方根.对于任意一个二次根式,我们知道:
(1)a为被开方数,为保证其有意义,可知a≥0;
(2) 表示一个数或式的算术平方根,可知≥0.
二次根式的被开方数非负
二次根式的值非负
二次根式的双重非负性
要点归纳
利用二次根式的双重非负性求字母的值
提示:多个非负数的和为零,则可得每个非负数均为零.初中阶段学过的非负数主要有绝对值、偶次幂及二次根式.
例3 若 ,求a -2b+c的值.
解:
由题意可知
解得a=-5,b=3,c=2.
所以a -2b+c=-5-2 6+2=-15.
素养考点1
解:由题意得x-y-1=0且x+y-3=0.
解得x=2,y=1.
∴4x+y=2×4+1=9,
∴x+4y的平方根为±3.
1.已知|x-y-1|和 互为相反数,求4x+y的平方根.
基础练习
二次根式的双重非负性和不等式求字母的值
例4 已知实数x、y满足等式 ,求x2-y2的值.
解:
由题意得
解得:x=5
把x=5,代入得y=6
所以x2-y2=52-62=-11
素养考点2
2. 已知y = ,求3x+2y的算术平方根.
解:由题意得
∴x=3,∴y=8,
∴3x+2y=3×3+2×8=25.
∵25的算术平方根为5,
∴3x+2y的算术平方根为5.
基础练习
二次根式的被开方数非负,即中a≥0
二次根式的值非负.即中≥0
二次根式的双重非负性
1.若二次根式有意义,求b的取值范围.
解:由题意得b-5≥0且b2-b-2≠0,
解得b≥5且b≠-1,b≠2,
∴b≥5.
查漏补缺
2.若x,y是实数,且y<,求的值.
解:根据题意得,
∴b=2.
∵y< ,
∴y< ,
∴ .
查漏补缺
解:由题意得b(b-2)≥0
由乘法法则得
解得b≥2 或b≤0
即当b≥2 或b≤0时, 有意义.
3.先阅读,后回答问题:当x为何值时,有意义?
提升能力
4.体会解题思想后,试着解答:当m为何值时, 有意义?
解:由题意得
,则
解得m≥2或m<
即当m≥2或m< 时, 有意义.
提升能力
课时2 二次根式的双重非负性
16.1 二次根式
透彻领悟二次根式的双重非负性本质,能够灵活运用该性质进行基础的运算与推理;熟练掌握运用二次根式双重非负性去处理代数式求值、等式成立判定等问题的技巧.
经由对诸多二次根式双重非负性相关例题、习题的深度分析与解答,强化逻辑思维与数学运算这两项核心能力.
当面临利用双重非负性解决较为复杂的问题(如多个非负项累加为零的情形)时,学会有条不紊地综合分析、层层推导的有效思维方式.
深切体会二次根式双重非负性在整个数学体系里的关键作用,强化对数学重要性质的重视程度与运用意识,进而激发对初中数学学习的浓厚兴趣.
1
2
3
4
【重点】透彻领悟二次根式的双重非负性本质.
【难点】灵活运用二次根式的双重非负性进行基础的运算与推理; 熟练掌握代数式求值、等式成立判定等问题的技巧.
二次根式的双重非负性
前者x为全体实数;后者x为正数和0.
当a>0时, 表示a的算术平方根,因此>0;
综上所述:当a≥0时, ≥0.
[问题1]当x是怎样的实数时,在实数范围内有意义? 呢?
[问题2]二次根式的被开方数a的取值范围是什么?它本身的取值范围又是什么?
当a=0时,表示0的算术平方根,因此=0.
二次根式的实质是表示一个非负数(或式)的算术平方根.对于任意一个二次根式,我们知道:
(1)a为被开方数,为保证其有意义,可知a≥0;
(2) 表示一个数或式的算术平方根,可知≥0.
二次根式的被开方数非负
二次根式的值非负
二次根式的双重非负性
要点归纳
利用二次根式的双重非负性求字母的值
提示:多个非负数的和为零,则可得每个非负数均为零.初中阶段学过的非负数主要有绝对值、偶次幂及二次根式.
例3 若 ,求a -2b+c的值.
解:
由题意可知
解得a=-5,b=3,c=2.
所以a -2b+c=-5-2 6+2=-15.
素养考点1
解:由题意得x-y-1=0且x+y-3=0.
解得x=2,y=1.
∴4x+y=2×4+1=9,
∴x+4y的平方根为±3.
1.已知|x-y-1|和 互为相反数,求4x+y的平方根.
基础练习
二次根式的双重非负性和不等式求字母的值
例4 已知实数x、y满足等式 ,求x2-y2的值.
解:
由题意得
解得:x=5
把x=5,代入得y=6
所以x2-y2=52-62=-11
素养考点2
2. 已知y = ,求3x+2y的算术平方根.
解:由题意得
∴x=3,∴y=8,
∴3x+2y=3×3+2×8=25.
∵25的算术平方根为5,
∴3x+2y的算术平方根为5.
基础练习
二次根式的被开方数非负,即中a≥0
二次根式的值非负.即中≥0
二次根式的双重非负性
1.若二次根式有意义,求b的取值范围.
解:由题意得b-5≥0且b2-b-2≠0,
解得b≥5且b≠-1,b≠2,
∴b≥5.
查漏补缺
2.若x,y是实数,且y<,求的值.
解:根据题意得,
∴b=2.
∵y< ,
∴y< ,
∴ .
查漏补缺
解:由题意得b(b-2)≥0
由乘法法则得
解得b≥2 或b≤0
即当b≥2 或b≤0时, 有意义.
3.先阅读,后回答问题:当x为何值时,有意义?
提升能力
4.体会解题思想后,试着解答:当m为何值时, 有意义?
解:由题意得
,则
解得m≥2或m<
即当m≥2或m< 时, 有意义.
提升能力
