16.1 课时3 二次根式性质及化简 课件(共30张PPT) 人教版数学八年级下册
文档属性
| 名称 | 16.1 课时3 二次根式性质及化简 课件(共30张PPT) 人教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-06 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
16.1 二次根式
课时3 二次根式性质及化简
能准确说出二次根式的两个重要性质,并能识别在不同情境下该运用哪条性质.
学会把二次根式化为最简二次根式,明确最简二次根式需满足被开方数不含分母且被开方数中不含能开得尽方的因数或因式这两个条件.
在探究二次根式性质的过程中,培养观察、分析、归纳等思维能力.
由于二次根式的性质运用和化简需要严格遵循相关规则,在学习过程中能促使学生养成严谨细致的学习习惯.
1
2
3
4
【重点】能准确说出二次根式的两个重要性质,并能识别在不同情境下该运用哪条性质.
【难点】在特殊情境中利用性质将二次根式化为最简二次根式.
1.怎样的式子叫二次根式?
2.怎样判断一个式子是不是二次根式?
3.如何确定二次根式中字母的取值范围?
一般地,我们把形如 (a≥0)的式子叫做二次根式.
(1)形式上: ;(2)被开方数a≥0.
①被开方数不小于零;
②分母中有字母时,要保证分母不为零.
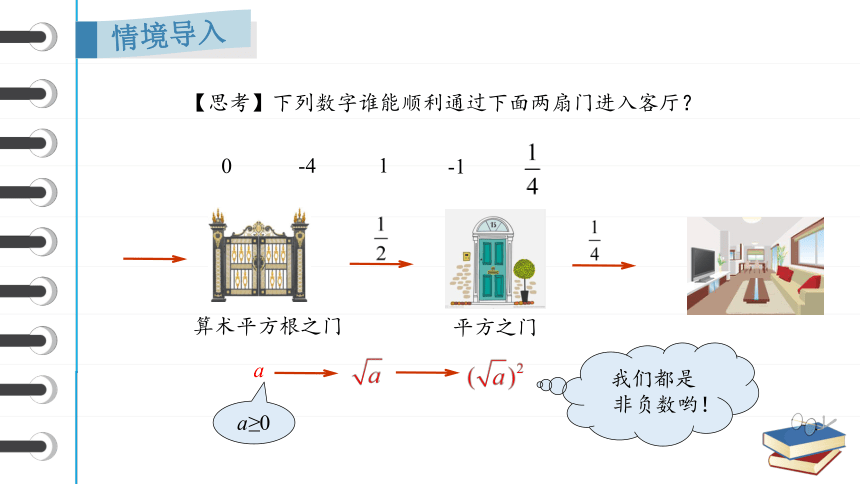
【思考】下列数字谁能顺利通过下面两扇门进入客厅?
算术平方根之门
平方之门
0
-4
-1
a
a≥0
1
我们都是
非负数哟!
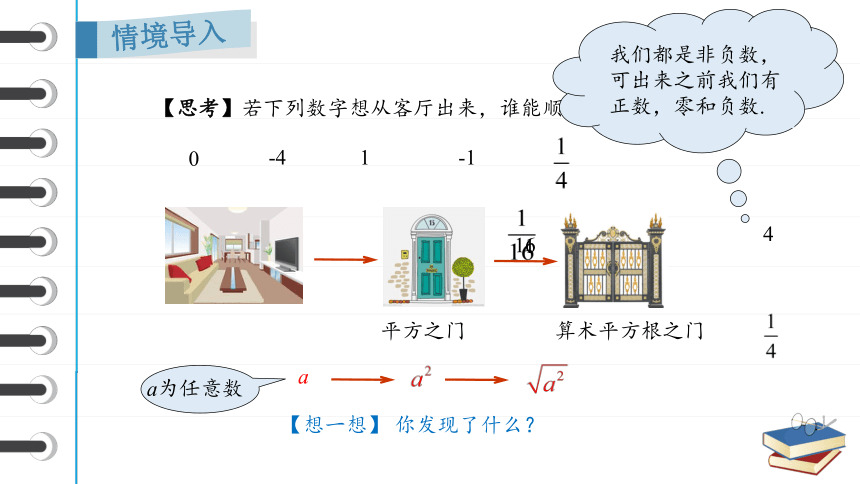
【思考】若下列数字想从客厅出来,谁能顺利通过两扇门出来呢?
算术平方根之门
平方之门
0
-4
-1
1
16
4
1
a
a为任意数
【想一想】 你发现了什么?
我们都是非负数,可出来之前我们有正数,零和负数.
(2)什么是一个数的算术平方根?如何表示?
(1)什么叫做一个数的平方根?如何表示?
一般地,若一个数的平方等于a,则这个数就叫做a的平方根.
若一个正数的平方等于a,则这个数就叫做a的算术平方根.
a的平方根是
用 (a≥0)表示.
(a≥0) 性质
知识点 1
(1)填空:
(2)通过(1)的思考,你能确定( ) (a≥0)的化简结果吗?说说你的理由.
4
0
2
同理, 分别是2, ,0的算术平方根,因此有
是4的算术平方根,根据算术平方根的意义,是一个平方等于4的非负数,因此有
的性质:
一般地, =a (a ≥0).
即一个非负数的算术平方根的平方等于它本身.
注意:不要忽略 a≥0 这一限制条件.这是使二次根式 有意义的前提条件.
要点归纳
例1 计算:
解:
积的乘方:(ab)2=a2b2
利用 的性质进行计算
(1) (2)
(1)
(2)
(2)可以用到幂的哪条基本性质呢?
素养考点1
【方法总结】本题逆用了 在实数范围内分解因式.
解:
利用 的性质分解因式
例2 在实数范围内分解因式:
(1)4x2-5 (2)m4-6m2+9
(1)
(2)
素养考点2
2
0.1
0
化简下列根式,想一想
的性质
化简后,你能确定 的化简结果吗?
知识点 2
算术平方根
平方运算
a
观察两者有什么关系?
填一填:
=a (a≥0).
...
观察两者有什么关系?
【猜一猜】当a<0时, =
?
-a
算术平方根
平方运算
a(a<0)
...
a (a≥0)
-a (a<0)
即任意一个数的平方的算术平方根等于它本身的绝对值.
的性质:
要点归纳
解:
利用 的性质进行计算
警示: 而3.14<π,要注意a的正负性.
例3 化简:
(1)
(2)
(3)
(4)
(1)
(2)
(3)
(4)
素养考点1
【讨论】(1)在 中,可否去掉“a≥0”?如果去掉“a≥0”,结论将会发生怎样的变化?
(2)第二小题中的 能否直接使用性质
进行化简?
计算 一般有两个步骤:
①去根号及被开方数的指数,写成绝对值的形式,即 ;
②去掉绝对值符号,即
要点归纳
4.请同学们快速分辨下列各题的对错.
( )
×
×
√
√
( )
( )
( )
基础练习
【议一议】如何区别 与 ?
从运算顺序看
从取值范围看
从运算结果看
先开方,后平方
先平方,后开方
a≥0
a取任何实数
a
|a|
意义
表示一个非负数a的算术平方根的平方
表示一个实数a的平方的算术平方根
解:由数轴可知a<0,b>0,a-b<0,
∴原式=|a|-|b|+|a-b|
=-a-b-(a-b)
=-2a.
例4 实数a、b在数轴上的对应点如图所示,请你化简:
a
b
几何图形与 的性质相结合的题目
素养考点2
5. 已知实数a、b在数轴上的对应点如图所示,化简.
解:由数轴可得:,,,
原式
.
【方法总结】利用数轴和二次根式的性质进行化简,关键是要要根据a,b的大小讨论绝对值内式子的符号.
a
b
0
基础练习
(1)含有数或表示数的字母;
(2)用基本运算符号连接数或表示数的字母.
回顾我们学过的式子,如
(a≥0)
这些式子有哪些共同
特征?
代数式的定义
知识点 3
用基本运算符号(基本运算包括加、减、乘、除、乘方和开方)把 或 连接起来的式子,我们称这样的式子为代数式.
数
表示数的字母
【想一想】到现在为止,初中阶段所学的代数式主要有哪几类?
代数式
整式
分式
二次根式
要点归纳
利用代数式的定义判断代数式
例5 下列式子:(1)x; (2)a-b; (3) ;(4) ;
(5)m=1+n;(6)2x>1;(7)-2.其中是代数式的有( )
A.4个 B.5个 C.6个 D.7个
B
素养考点1
6.下列式子是代数式的有 ( )
①a2+b2 ; ② ; ③13; ④x=2; ⑤3×(4 -5);
⑥x-1≤0; ⑦10x+5y=15 ; ⑧
A.3个 B.4个 C.5个 D.6个
C
7.如图,是一个圆形挂钟,正面面积为S,用代数式表示出钟的半径为__________.
基础练习
二次根式
性质
拓展性质
=a (a ≥0).
代数式
整式
分式
二次根式
(a为全体实数)
1.填空:
_____;(2)_____;
(3)_______.
13
2. 当2A.3 B.-3 C.1 D.-1
D
3. 计算:
4.(1)已知a为实数,求代数式 的值.
解:由题意得a+2≥0,-4-2a≥0,
∴a=-2,
∴ .
(2)已知a为实数,求代数式 的值.
解:由题意得-a2≥0,又∵a2≥0,
∴a2=0,∴a=0,
∴
16.1 二次根式
课时3 二次根式性质及化简
能准确说出二次根式的两个重要性质,并能识别在不同情境下该运用哪条性质.
学会把二次根式化为最简二次根式,明确最简二次根式需满足被开方数不含分母且被开方数中不含能开得尽方的因数或因式这两个条件.
在探究二次根式性质的过程中,培养观察、分析、归纳等思维能力.
由于二次根式的性质运用和化简需要严格遵循相关规则,在学习过程中能促使学生养成严谨细致的学习习惯.
1
2
3
4
【重点】能准确说出二次根式的两个重要性质,并能识别在不同情境下该运用哪条性质.
【难点】在特殊情境中利用性质将二次根式化为最简二次根式.
1.怎样的式子叫二次根式?
2.怎样判断一个式子是不是二次根式?
3.如何确定二次根式中字母的取值范围?
一般地,我们把形如 (a≥0)的式子叫做二次根式.
(1)形式上: ;(2)被开方数a≥0.
①被开方数不小于零;
②分母中有字母时,要保证分母不为零.
【思考】下列数字谁能顺利通过下面两扇门进入客厅?
算术平方根之门
平方之门
0
-4
-1
a
a≥0
1
我们都是
非负数哟!
【思考】若下列数字想从客厅出来,谁能顺利通过两扇门出来呢?
算术平方根之门
平方之门
0
-4
-1
1
16
4
1
a
a为任意数
【想一想】 你发现了什么?
我们都是非负数,可出来之前我们有正数,零和负数.
(2)什么是一个数的算术平方根?如何表示?
(1)什么叫做一个数的平方根?如何表示?
一般地,若一个数的平方等于a,则这个数就叫做a的平方根.
若一个正数的平方等于a,则这个数就叫做a的算术平方根.
a的平方根是
用 (a≥0)表示.
(a≥0) 性质
知识点 1
(1)填空:
(2)通过(1)的思考,你能确定( ) (a≥0)的化简结果吗?说说你的理由.
4
0
2
同理, 分别是2, ,0的算术平方根,因此有
是4的算术平方根,根据算术平方根的意义,是一个平方等于4的非负数,因此有
的性质:
一般地, =a (a ≥0).
即一个非负数的算术平方根的平方等于它本身.
注意:不要忽略 a≥0 这一限制条件.这是使二次根式 有意义的前提条件.
要点归纳
例1 计算:
解:
积的乘方:(ab)2=a2b2
利用 的性质进行计算
(1) (2)
(1)
(2)
(2)可以用到幂的哪条基本性质呢?
素养考点1
【方法总结】本题逆用了 在实数范围内分解因式.
解:
利用 的性质分解因式
例2 在实数范围内分解因式:
(1)4x2-5 (2)m4-6m2+9
(1)
(2)
素养考点2
2
0.1
0
化简下列根式,想一想
的性质
化简后,你能确定 的化简结果吗?
知识点 2
算术平方根
平方运算
a
观察两者有什么关系?
填一填:
=a (a≥0).
...
观察两者有什么关系?
【猜一猜】当a<0时, =
?
-a
算术平方根
平方运算
a(a<0)
...
a (a≥0)
-a (a<0)
即任意一个数的平方的算术平方根等于它本身的绝对值.
的性质:
要点归纳
解:
利用 的性质进行计算
警示: 而3.14<π,要注意a的正负性.
例3 化简:
(1)
(2)
(3)
(4)
(1)
(2)
(3)
(4)
素养考点1
【讨论】(1)在 中,可否去掉“a≥0”?如果去掉“a≥0”,结论将会发生怎样的变化?
(2)第二小题中的 能否直接使用性质
进行化简?
计算 一般有两个步骤:
①去根号及被开方数的指数,写成绝对值的形式,即 ;
②去掉绝对值符号,即
要点归纳
4.请同学们快速分辨下列各题的对错.
( )
×
×
√
√
( )
( )
( )
基础练习
【议一议】如何区别 与 ?
从运算顺序看
从取值范围看
从运算结果看
先开方,后平方
先平方,后开方
a≥0
a取任何实数
a
|a|
意义
表示一个非负数a的算术平方根的平方
表示一个实数a的平方的算术平方根
解:由数轴可知a<0,b>0,a-b<0,
∴原式=|a|-|b|+|a-b|
=-a-b-(a-b)
=-2a.
例4 实数a、b在数轴上的对应点如图所示,请你化简:
a
b
几何图形与 的性质相结合的题目
素养考点2
5. 已知实数a、b在数轴上的对应点如图所示,化简.
解:由数轴可得:,,,
原式
.
【方法总结】利用数轴和二次根式的性质进行化简,关键是要要根据a,b的大小讨论绝对值内式子的符号.
a
b
0
基础练习
(1)含有数或表示数的字母;
(2)用基本运算符号连接数或表示数的字母.
回顾我们学过的式子,如
(a≥0)
这些式子有哪些共同
特征?
代数式的定义
知识点 3
用基本运算符号(基本运算包括加、减、乘、除、乘方和开方)把 或 连接起来的式子,我们称这样的式子为代数式.
数
表示数的字母
【想一想】到现在为止,初中阶段所学的代数式主要有哪几类?
代数式
整式
分式
二次根式
要点归纳
利用代数式的定义判断代数式
例5 下列式子:(1)x; (2)a-b; (3) ;(4) ;
(5)m=1+n;(6)2x>1;(7)-2.其中是代数式的有( )
A.4个 B.5个 C.6个 D.7个
B
素养考点1
6.下列式子是代数式的有 ( )
①a2+b2 ; ② ; ③13; ④x=2; ⑤3×(4 -5);
⑥x-1≤0; ⑦10x+5y=15 ; ⑧
A.3个 B.4个 C.5个 D.6个
C
7.如图,是一个圆形挂钟,正面面积为S,用代数式表示出钟的半径为__________.
基础练习
二次根式
性质
拓展性质
=a (a ≥0).
代数式
整式
分式
二次根式
(a为全体实数)
1.填空:
_____;(2)_____;
(3)_______.
13
2. 当2
D
3. 计算:
4.(1)已知a为实数,求代数式 的值.
解:由题意得a+2≥0,-4-2a≥0,
∴a=-2,
∴ .
(2)已知a为实数,求代数式 的值.
解:由题意得-a2≥0,又∵a2≥0,
∴a2=0,∴a=0,
∴
