16.2 课时1 二次根式的乘法 课件(共24张PPT) 人教版数学八年级下册
文档属性
| 名称 | 16.2 课时1 二次根式的乘法 课件(共24张PPT) 人教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-06 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
16.2 二次根式的乘除
课时1 二次根式的乘法
理解二次根式乘法法则的推导过程,知道其适用条件.
能够熟练运用二次根式乘法法则进行二次根式的乘法运算;会利用二次根式乘法法则将被开方数中含有完全平方因数的二次根式进行化简.在运算和化简过程中,养成认真、严谨的学习态度,认识到准确运算的重要性.
通过对二次根式乘法法则的推导过程,培养逻辑推理能力,体会从特殊到一般的数学思维方法.
在学习二次根式乘法法则及其应用过程中,体会数学公式的简洁性和规律性,感受数学的美感.
1
2
3
4
【重点】理解二次根式乘法法则的推导过程,并能够熟练运用二次根式乘法法则进行二次根式的乘法运算.
【难点】通过对二次根式乘法法则的推导过程,培养逻辑推理能力,体会从特殊到一般的数学思维方法.
(a≥0)
(1)
(2)
a
-a
|a|=
a
当a≥0时
当a<0时
学过的二次根式有哪些性质?
苹果ios手持操作系统的图标为圆角矩形,长为 cm,宽为 cm,则它的面积是多少呢?
如何计算 ?
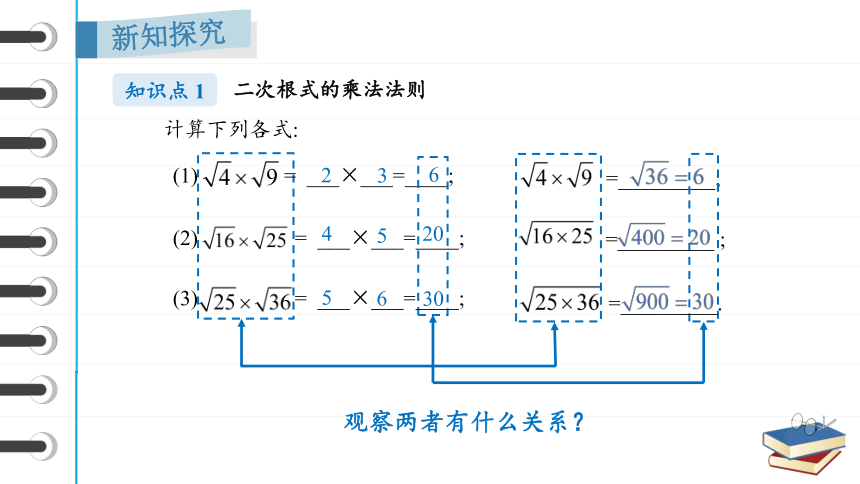
(1) = ___×___=____;
=_________;
计算下列各式:
2
3
6
4
5
20
5
6
30
(2) = ___×___=____;
观察两者有什么关系?
二次根式的乘法法则
(3) = ___×___=____;
=_________ ;
=_________.
知识点 1
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
你发现了什么规律?你能用字母表示你所发现的规律吗?
猜测:
你能证明这个猜测吗?
求证:
证明:根据积的乘方法则,有
∴
就是ab的算术平方根.
又∵ 表示ab的算术平方根,
∴ .
不成立!
【思考】
成立吗?
没有意义
因此被开方数a,b需要满足什么条件?
a,b是非负数,即a≥0,b≥0
语言表述:
算术平方根的积等于各个被开方数积的算术平方根.
二次根式的乘法法则是:
二次根式相乘,________不变,________相乘.
根指数
被开方数
注意:a,b都必须是非负数.
要点归纳
例1 计算:
解:
简单的二次根式的乘法运算
(1) (2)
(1)
(2)
素养考点1
【想一想】下边的式子如何运算?
解:
【方法总结】只需其中两个结合就可实现转化进行计算,说明二次根式乘法法则同样适合三个及三个以上的二次根式相乘( )
可先用乘法结合律,再运用二次根式的乘法法则
1.计算
基础练习
思考:
计算:
你还记得单项式乘单项式法则吗?
计算2a2·3a2= .
类比思维
例2
解:
因数不是1二次根式的乘法运算
解:
【方法总结】:当二次根式根号外的因数不为1时,可类比单项式乘单项式的法则计算,即
素养考点2
2.计算:
解:
=20×18=360
(1) (2)
(2)
(1)
基础练习
二次根式的乘法法则的推广:
①多个二次根式相乘时此法则也适用,即
②当二次根号外有因数(式)时,可以类比单项式乘单 项式的法则计算,即根号外的因数(式)的积作为根号外的因数(式),被开方数的积作为被开方数,即
要点归纳
反过来:
(a≥0,b≥0)
(a≥0,b≥0)
一般的:
我们可以运用它来进行二次根式的解题和化简.
语言表述:积的算术平方根,等于积中各因式的算术平方根的积.
二次根式的乘法法则的逆用
知识点2
例3 化简:
(1) ; (2) .
(2)中4a2b3含有像4,a2,b2,这样开的尽方的因数或因式,把它们开方后移到根号外.
利用二次根式的乘法法则的逆用计算
=
解:(1)
= 4 ×9
=36
(2)
=
=
=
素养考点1
3.化简:
【方法总结】化简二次根式,就要把被开方数中的平方数(或平方式)从根号里开出来.
解:
(1)
(2)
(3)
(1)
(2)
(3)
基础练习
例4 计算:
(1) ;(2) ;(3) .
利用二次根式的乘法法则及逆用计算
解:(1)
(2)
(3)
素养考点2
方法点拨
化简二次根式的步骤:
1.把被开方数分解因式(或因数) ;
2.把各因式(或因数)积的算术平方根化为每个因式(或因数的算术平方根的积;
3.如果因式中有平方式(或平方数),应用关系式
把这个因式(或因数)开出来,将二次根式化简 .
要点归纳
二次根式乘法
法则
性质
拓展法则
A. B.
C. D.
1.计算 的结果是 ( )
A. B.3 C. D.2
C
2.下面计算结果正确的是 ( )
D
3.当时,化简的结果是( )
A. B. C. D.
C
4.若 ,则( )
A.a≥6 B.a≥0
C.0≤a≤6 D.a为一切实数
A
5.化简
16.2 二次根式的乘除
课时1 二次根式的乘法
理解二次根式乘法法则的推导过程,知道其适用条件.
能够熟练运用二次根式乘法法则进行二次根式的乘法运算;会利用二次根式乘法法则将被开方数中含有完全平方因数的二次根式进行化简.在运算和化简过程中,养成认真、严谨的学习态度,认识到准确运算的重要性.
通过对二次根式乘法法则的推导过程,培养逻辑推理能力,体会从特殊到一般的数学思维方法.
在学习二次根式乘法法则及其应用过程中,体会数学公式的简洁性和规律性,感受数学的美感.
1
2
3
4
【重点】理解二次根式乘法法则的推导过程,并能够熟练运用二次根式乘法法则进行二次根式的乘法运算.
【难点】通过对二次根式乘法法则的推导过程,培养逻辑推理能力,体会从特殊到一般的数学思维方法.
(a≥0)
(1)
(2)
a
-a
|a|=
a
当a≥0时
当a<0时
学过的二次根式有哪些性质?
苹果ios手持操作系统的图标为圆角矩形,长为 cm,宽为 cm,则它的面积是多少呢?
如何计算 ?
(1) = ___×___=____;
=_________;
计算下列各式:
2
3
6
4
5
20
5
6
30
(2) = ___×___=____;
观察两者有什么关系?
二次根式的乘法法则
(3) = ___×___=____;
=_________ ;
=_________.
知识点 1
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
你发现了什么规律?你能用字母表示你所发现的规律吗?
猜测:
你能证明这个猜测吗?
求证:
证明:根据积的乘方法则,有
∴
就是ab的算术平方根.
又∵ 表示ab的算术平方根,
∴ .
不成立!
【思考】
成立吗?
没有意义
因此被开方数a,b需要满足什么条件?
a,b是非负数,即a≥0,b≥0
语言表述:
算术平方根的积等于各个被开方数积的算术平方根.
二次根式的乘法法则是:
二次根式相乘,________不变,________相乘.
根指数
被开方数
注意:a,b都必须是非负数.
要点归纳
例1 计算:
解:
简单的二次根式的乘法运算
(1) (2)
(1)
(2)
素养考点1
【想一想】下边的式子如何运算?
解:
【方法总结】只需其中两个结合就可实现转化进行计算,说明二次根式乘法法则同样适合三个及三个以上的二次根式相乘( )
可先用乘法结合律,再运用二次根式的乘法法则
1.计算
基础练习
思考:
计算:
你还记得单项式乘单项式法则吗?
计算2a2·3a2= .
类比思维
例2
解:
因数不是1二次根式的乘法运算
解:
【方法总结】:当二次根式根号外的因数不为1时,可类比单项式乘单项式的法则计算,即
素养考点2
2.计算:
解:
=20×18=360
(1) (2)
(2)
(1)
基础练习
二次根式的乘法法则的推广:
①多个二次根式相乘时此法则也适用,即
②当二次根号外有因数(式)时,可以类比单项式乘单 项式的法则计算,即根号外的因数(式)的积作为根号外的因数(式),被开方数的积作为被开方数,即
要点归纳
反过来:
(a≥0,b≥0)
(a≥0,b≥0)
一般的:
我们可以运用它来进行二次根式的解题和化简.
语言表述:积的算术平方根,等于积中各因式的算术平方根的积.
二次根式的乘法法则的逆用
知识点2
例3 化简:
(1) ; (2) .
(2)中4a2b3含有像4,a2,b2,这样开的尽方的因数或因式,把它们开方后移到根号外.
利用二次根式的乘法法则的逆用计算
=
解:(1)
= 4 ×9
=36
(2)
=
=
=
素养考点1
3.化简:
【方法总结】化简二次根式,就要把被开方数中的平方数(或平方式)从根号里开出来.
解:
(1)
(2)
(3)
(1)
(2)
(3)
基础练习
例4 计算:
(1) ;(2) ;(3) .
利用二次根式的乘法法则及逆用计算
解:(1)
(2)
(3)
素养考点2
方法点拨
化简二次根式的步骤:
1.把被开方数分解因式(或因数) ;
2.把各因式(或因数)积的算术平方根化为每个因式(或因数的算术平方根的积;
3.如果因式中有平方式(或平方数),应用关系式
把这个因式(或因数)开出来,将二次根式化简 .
要点归纳
二次根式乘法
法则
性质
拓展法则
A. B.
C. D.
1.计算 的结果是 ( )
A. B.3 C. D.2
C
2.下面计算结果正确的是 ( )
D
3.当时,化简的结果是( )
A. B. C. D.
C
4.若 ,则( )
A.a≥6 B.a≥0
C.0≤a≤6 D.a为一切实数
A
5.化简
