16.2 课时2 二次根式的除法 课件(共30张PPT) 人教版数学八年级下册
文档属性
| 名称 | 16.2 课时2 二次根式的除法 课件(共30张PPT) 人教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-06 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
16.2 二次根式的乘除
课时2 二次根式的除法
理解二次根式的除法法则,能准确表述该法则内容;会运用二次根式的除法法则进行二次根式的除法运算,掌握分母有理化的方法,能将二次根式化为最简二次根式.
通过与二次根式乘法的学习过程进行类比,培养类比推理的能力,更好地理解和掌握二次根式除法的相关知识和运算技巧.
感受二次根式除法运算在化简根式、解决实际数学问题等方面的作用,体会数学知识之间的内在联系以及数学的简洁.
1
2
3
【重点】理解二次根式除法法则,并能够熟练运用二次根式除法法则进行二次根式的除法运算
【难点】掌握把分母中含有二次根式的式子进行分母有理化的方法并能够熟练运用.
二次根式乘法
法则
性质
(计算)
(化简)
站在水平高度为h米的地方看到可见的水平距离为d米,它们近似地符合公式为 .
问题1 某一登山者爬到海拔100米处,即 时,他看到的水平线的距离d1是多少?
问题2 该登山者接着爬到海拔200米的山顶,即 时,此时他看到的水平线的距离d2是多少?
问题3 他从海拔100米处登上海拔200米高的山顶,那么他看到的水平线的距离是原来的多少倍?
【思考】乘法法则是如何得出的?二次根式的除法该怎样算呢?除法有没有类似的法则?
二次根式的除法该怎样算呢?
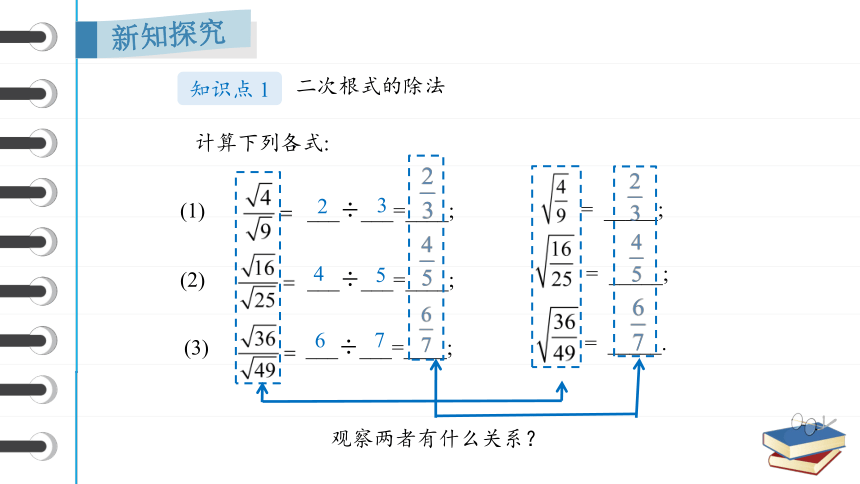
(1) ___÷___=____;
= _____;
计算下列各式:
(2) ___÷___=____;
(3) ___÷___=____;
= _____;
= _____.
2
3
4
5
6
7
观察两者有什么关系?
二次根式的除法
知识点 1
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
猜想 通过上述二次根式除法运算结果,联想二次根式乘法运算法则,你能说出二次根式 的结果吗?
特殊
一般
在前面发现的规律 中,a,b的取值范围有没有限制呢?
a,b同号就可以啦
你们都错啦,
a≥0,b>0, 当b=0时
等式两边的二次根式就没有意义啦
不对,同乘法法则一样,a,b都为非负数.
二次根式的除法法则:
文字叙述:
算术平方根的商等于被开方数商的算术平方根.
当二次根式根号外的因数(式)不为1时,可类比单项式除以单项式法则,易得
要点归纳
例1 计算:
解:
利用二次根式的除法法则计算根号外因数是1的二次根式
提示:像(2)中除式是分数或分式时,先要转化为乘法
再进行运算.
(1)
(2)
(1)
(2)
素养考点1
1.计算:
解:
(1)
(2)
(3)
(1)
(2)
(3)
基础练习
解:
利用二次根式的除法法则计算根号外因数不是1的二次根式
例2 计算:
(1)
(2)
(1)
(2)
素养考点2
【方法总结】类似(2)中被开方数中含有带分数,应先将带分
数化成假分数,再运用二次根式除法法则进行运算.
2.计算,看谁算的既对又快.
(1)
(2)
基础练习
我们可以运用它来进行二次根式的化简.
语言表述:商的算术平方根,等于被除式的算术平方根除以除式的算术平方根.
我们知道,把二次根式的乘法法则反过来就得到积的算术平方根的性质.
类似地,把二次根式的除法法则反过来,就得到二次根式的商的算术平方根的性质:
商的算术平方根的性质
知识点 2
解:
补充解法:
商的算术平方根的性质的应用
例3 化简:
(1)
(2)
(1)
(2)
还有其它解法吗
素养考点1
解:
【方法总结】像(3)可以先用商的算术平方根的性质,再运用积的算术平方根性质.
(1)
(2)
(1)
(2)
(3)
(3)
3.化简
基础练习
解: (1)
(2)
(1) (2) (3)
问题1 计算:
(3)
最简二次根式
知识点 3
问题2 观察上面各小题计算的最后结果并思考:
(1)你觉得这些结果能否再化简,它们是否已经最简了?
(2)这些结果有什么共同特点,类比最简分数,你认为一个二次根式满足什么条件就可以说它是最简了?
有如下两个特点:
(1)被开方数不含分母;
(2)被开方数中所有因数(或因式)的幂的指数都小于2.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
最简二次根式应满足的条件:
(1)被开方数不含分母或分母中不含____________;
(2)被开方数中不含____________的因数或因式.
注:当被开方数是整式时要先判断是否能够分解因式,然后再观察各个因式的指数是否是2(或大于2的整数),若是则说明含有能开方的因式,不满足条件,不是最简二次根式.
二次根式
能开得尽方
要点归纳
解:
分母有理化
总结:分母形如 的式子,分子、分母同乘以 可使
分母不含根号.
例4 计算:
(1)
(2)
(3)
(2)
(3)
(1)
素养考点1
4.
下列代数式中,是最简二次根式( )
(A)
(B)
(C)
(D)
C
被开方数中
含有分母
被开方数中的8
还可以再开方
被开方数中的9和b2 还可以再开方
基础练习
化成最简二次根式的一般方法
(1)将被开方数中能开得尽方的因数或者因式进行开方,
如
(2)若被开方数中含有带分数,应先将带分数化成假分数,再去分母,并将能开得尽方的因数或者因式进行开方,如
(3)若被开方数中含有小数,应先将小数化成分数后再进行化简,如
要点归纳
设长方形的面积为S,相邻两边长分别为a,b.已知 ,求a的值.
解:∵
二次根式的应用
∴
知识点 4
6. 高空抛物现象被称为“悬在城市上空的痛”.据报道:一个30g的鸡蛋从18楼抛下来就可以砸破行人的头骨,从25楼抛下可以使人当场死亡.据研究从高空抛物时间t和高度h近似的满足公式 .从100米高空抛物到落地所需时间t2是从50米高空抛物到落地所需时间t1的多少倍?
解:由题意得
基础练习
二次根式除法
法则
性质
拓展法则
相关概念
分母有理化
最简二次根式
2.若 都是最简二次根式,则a、b的值分别是( )
(A) a=1,b=-2 (B) a=1,b=1
(C) a=0,b=1
(D)
C
1.下列是最简二次根式是( )
B
A. B. C. D.
3.把下列二次根式化成最简二次根式:
(1)
(2)
解:(1)
(2)
(1)
解:原式=
(2)
解:原式=
4.化简
5.已知,实数x、y满足: ,求 的值.
解:由已知,可得
2y-6≥0
12-4y≥0
解得
y=3
则
x=2
原式=
16.2 二次根式的乘除
课时2 二次根式的除法
理解二次根式的除法法则,能准确表述该法则内容;会运用二次根式的除法法则进行二次根式的除法运算,掌握分母有理化的方法,能将二次根式化为最简二次根式.
通过与二次根式乘法的学习过程进行类比,培养类比推理的能力,更好地理解和掌握二次根式除法的相关知识和运算技巧.
感受二次根式除法运算在化简根式、解决实际数学问题等方面的作用,体会数学知识之间的内在联系以及数学的简洁.
1
2
3
【重点】理解二次根式除法法则,并能够熟练运用二次根式除法法则进行二次根式的除法运算
【难点】掌握把分母中含有二次根式的式子进行分母有理化的方法并能够熟练运用.
二次根式乘法
法则
性质
(计算)
(化简)
站在水平高度为h米的地方看到可见的水平距离为d米,它们近似地符合公式为 .
问题1 某一登山者爬到海拔100米处,即 时,他看到的水平线的距离d1是多少?
问题2 该登山者接着爬到海拔200米的山顶,即 时,此时他看到的水平线的距离d2是多少?
问题3 他从海拔100米处登上海拔200米高的山顶,那么他看到的水平线的距离是原来的多少倍?
【思考】乘法法则是如何得出的?二次根式的除法该怎样算呢?除法有没有类似的法则?
二次根式的除法该怎样算呢?
(1) ___÷___=____;
= _____;
计算下列各式:
(2) ___÷___=____;
(3) ___÷___=____;
= _____;
= _____.
2
3
4
5
6
7
观察两者有什么关系?
二次根式的除法
知识点 1
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
猜想 通过上述二次根式除法运算结果,联想二次根式乘法运算法则,你能说出二次根式 的结果吗?
特殊
一般
在前面发现的规律 中,a,b的取值范围有没有限制呢?
a,b同号就可以啦
你们都错啦,
a≥0,b>0, 当b=0时
等式两边的二次根式就没有意义啦
不对,同乘法法则一样,a,b都为非负数.
二次根式的除法法则:
文字叙述:
算术平方根的商等于被开方数商的算术平方根.
当二次根式根号外的因数(式)不为1时,可类比单项式除以单项式法则,易得
要点归纳
例1 计算:
解:
利用二次根式的除法法则计算根号外因数是1的二次根式
提示:像(2)中除式是分数或分式时,先要转化为乘法
再进行运算.
(1)
(2)
(1)
(2)
素养考点1
1.计算:
解:
(1)
(2)
(3)
(1)
(2)
(3)
基础练习
解:
利用二次根式的除法法则计算根号外因数不是1的二次根式
例2 计算:
(1)
(2)
(1)
(2)
素养考点2
【方法总结】类似(2)中被开方数中含有带分数,应先将带分
数化成假分数,再运用二次根式除法法则进行运算.
2.计算,看谁算的既对又快.
(1)
(2)
基础练习
我们可以运用它来进行二次根式的化简.
语言表述:商的算术平方根,等于被除式的算术平方根除以除式的算术平方根.
我们知道,把二次根式的乘法法则反过来就得到积的算术平方根的性质.
类似地,把二次根式的除法法则反过来,就得到二次根式的商的算术平方根的性质:
商的算术平方根的性质
知识点 2
解:
补充解法:
商的算术平方根的性质的应用
例3 化简:
(1)
(2)
(1)
(2)
还有其它解法吗
素养考点1
解:
【方法总结】像(3)可以先用商的算术平方根的性质,再运用积的算术平方根性质.
(1)
(2)
(1)
(2)
(3)
(3)
3.化简
基础练习
解: (1)
(2)
(1) (2) (3)
问题1 计算:
(3)
最简二次根式
知识点 3
问题2 观察上面各小题计算的最后结果并思考:
(1)你觉得这些结果能否再化简,它们是否已经最简了?
(2)这些结果有什么共同特点,类比最简分数,你认为一个二次根式满足什么条件就可以说它是最简了?
有如下两个特点:
(1)被开方数不含分母;
(2)被开方数中所有因数(或因式)的幂的指数都小于2.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
最简二次根式应满足的条件:
(1)被开方数不含分母或分母中不含____________;
(2)被开方数中不含____________的因数或因式.
注:当被开方数是整式时要先判断是否能够分解因式,然后再观察各个因式的指数是否是2(或大于2的整数),若是则说明含有能开方的因式,不满足条件,不是最简二次根式.
二次根式
能开得尽方
要点归纳
解:
分母有理化
总结:分母形如 的式子,分子、分母同乘以 可使
分母不含根号.
例4 计算:
(1)
(2)
(3)
(2)
(3)
(1)
素养考点1
4.
下列代数式中,是最简二次根式( )
(A)
(B)
(C)
(D)
C
被开方数中
含有分母
被开方数中的8
还可以再开方
被开方数中的9和b2 还可以再开方
基础练习
化成最简二次根式的一般方法
(1)将被开方数中能开得尽方的因数或者因式进行开方,
如
(2)若被开方数中含有带分数,应先将带分数化成假分数,再去分母,并将能开得尽方的因数或者因式进行开方,如
(3)若被开方数中含有小数,应先将小数化成分数后再进行化简,如
要点归纳
设长方形的面积为S,相邻两边长分别为a,b.已知 ,求a的值.
解:∵
二次根式的应用
∴
知识点 4
6. 高空抛物现象被称为“悬在城市上空的痛”.据报道:一个30g的鸡蛋从18楼抛下来就可以砸破行人的头骨,从25楼抛下可以使人当场死亡.据研究从高空抛物时间t和高度h近似的满足公式 .从100米高空抛物到落地所需时间t2是从50米高空抛物到落地所需时间t1的多少倍?
解:由题意得
基础练习
二次根式除法
法则
性质
拓展法则
相关概念
分母有理化
最简二次根式
2.若 都是最简二次根式,则a、b的值分别是( )
(A) a=1,b=-2 (B) a=1,b=1
(C) a=0,b=1
(D)
C
1.下列是最简二次根式是( )
B
A. B. C. D.
3.把下列二次根式化成最简二次根式:
(1)
(2)
解:(1)
(2)
(1)
解:原式=
(2)
解:原式=
4.化简
5.已知,实数x、y满足: ,求 的值.
解:由已知,可得
2y-6≥0
12-4y≥0
解得
y=3
则
x=2
原式=
