2025届高考物理二轮复习:专题一 力与运动 第3讲 力与曲线运动(A) -专项训练(含解析)
文档属性
| 名称 | 2025届高考物理二轮复习:专题一 力与运动 第3讲 力与曲线运动(A) -专项训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 177.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-05 11:23:28 | ||
图片预览


文档简介
2025届高考物理二轮复习
专题一 力与运动 第3讲 力与曲线运动(A) -专项训练
1.[2024·温州模拟] 如图所示为某段河流,河水沿着河床做曲线运动.图中A、B、C、D四处中,受河水冲击最严重的是 ( )
A.A处 B.B处
C.C处 D.D处
2.[2024·金华模拟] 如图所示为“玉兔二号”巡视器在月球上从O处行走到B处的照片.轨迹OA段是直线,AB段是曲线,巡视器质量为135 kg,则巡视器 ( )
A.受到月球的引力为1350 N
B.在AB段运动时一定有加速度
C.在OA段与AB段的平均速度方向相同
D.从O到B的位移大小等于OAB的轨迹长度
3.(不定项)[2024·桐乡一中模拟] 芬兰小将拉林托以两跳240.9分的成绩在跳台滑雪世界杯芬兰站中获得冠军.如图所示是简化后的跳台滑雪的雪道示意图,拉林托从助滑雪道AB上由静止开始滑下,到达C点后水平飞出,落到倾斜直滑道上的D点,E是运动轨迹上的某一点,在该点拉林托的速度方向与直滑道CD平行.设拉林托从C到E与从E到D的运动时间分别为t1、t2,EF垂直于CD,忽略空气阻力,则( )
A.t1=t2
B.t1>t2
C.=
D.>
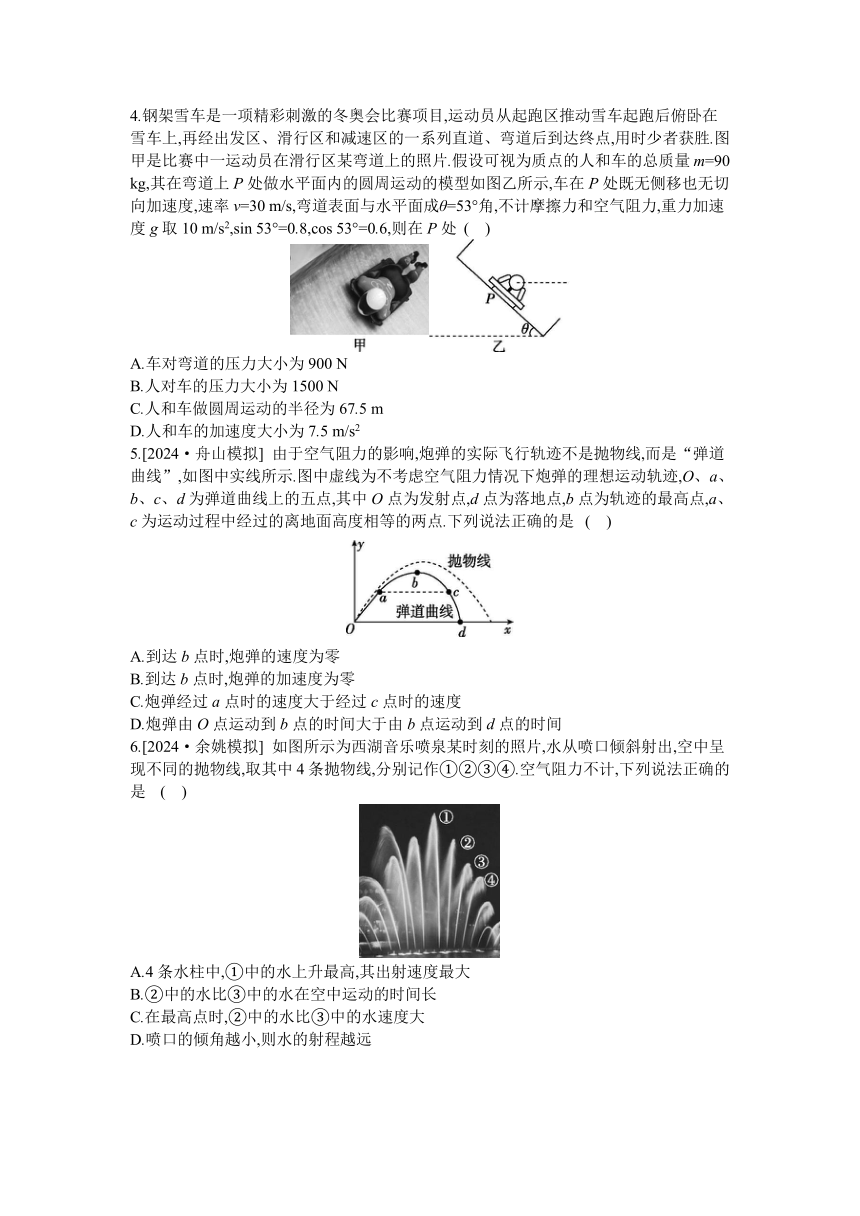
4.钢架雪车是一项精彩刺激的冬奥会比赛项目,运动员从起跑区推动雪车起跑后俯卧在雪车上,再经出发区、滑行区和减速区的一系列直道、弯道后到达终点,用时少者获胜.图甲是比赛中一运动员在滑行区某弯道上的照片.假设可视为质点的人和车的总质量m=90 kg,其在弯道上P处做水平面内的圆周运动的模型如图乙所示,车在P处既无侧移也无切向加速度,速率v=30 m/s,弯道表面与水平面成θ=53°角,不计摩擦力和空气阻力,重力加速度g取10 m/s2,sin 53°=0.8,cos 53°=0.6,则在P处 ( )
A.车对弯道的压力大小为900 N
B.人对车的压力大小为1500 N
C.人和车做圆周运动的半径为67.5 m
D.人和车的加速度大小为7.5 m/s2
5.[2024·舟山模拟] 由于空气阻力的影响,炮弹的实际飞行轨迹不是抛物线,而是“弹道曲线”,如图中实线所示.图中虚线为不考虑空气阻力情况下炮弹的理想运动轨迹,O、a、b、c、d为弹道曲线上的五点,其中O点为发射点,d点为落地点,b点为轨迹的最高点,a、c为运动过程中经过的离地面高度相等的两点.下列说法正确的是 ( )
A.到达b点时,炮弹的速度为零
B.到达b点时,炮弹的加速度为零
C.炮弹经过a点时的速度大于经过c点时的速度
D.炮弹由O点运动到b点的时间大于由b点运动到d点的时间
6.[2024·余姚模拟] 如图所示为西湖音乐喷泉某时刻的照片,水从喷口倾斜射出,空中呈现不同的抛物线,取其中4条抛物线,分别记作①②③④.空气阻力不计,下列说法正确的是 ( )
A.4条水柱中,①中的水上升最高,其出射速度最大
B.②中的水比③中的水在空中运动的时间长
C.在最高点时,②中的水比③中的水速度大
D.喷口的倾角越小,则水的射程越远
7.[2022·北京卷] 我国航天员在“天宫课堂”中演示了多种有趣的实验,提高了青少年科学探索的兴趣.某同学设计了如下实验:细绳一端固定,另一端系一小球,给小球一初速度使其在竖直平面内做圆周运动.无论在“天宫”还是在地面做此实验 ( )
A. 小球的速度大小均发生变化
B. 小球的向心加速度大小均发生变化
C. 细绳的拉力对小球均不做功
D. 细绳的拉力大小均发生变化
8.[2024·镇海中学模拟] 如图所示,轻杆两端分别固定着可以视为质点的小球A、B,放置在光滑水平桌面上,杆上O点处穿过一竖直转动轴,A、B的质量之比mA∶mB=4∶1,A、B到O点的距离之比rA∶rB=1∶2.当轻杆绕轴匀速转动时,下列说法正确的是 ( )
A.A对杆的作用力大小等于B对杆的作用力大小
B.A的向心加速度大小大于B的向心加速度大小
C.A的动能等于B的动能
D.A的周期小于B的周期
9.(不定项)如图所示,在地面上方的水平匀强电场中,一个质量为m、电荷量为+q的小球系在一根长为d的绝缘细线一端,可以在竖直平面内绕O点做圆周运动.AB为圆周的水平直径,CD为竖直直径.已知重力加速度为g,电场强度E=,下列说法正确的是( )
A.若小球恰能在竖直平面内绕O点做圆周运动,则它运动的最小速度为
B.若小球在竖直平面内绕O点做圆周运动,则小球运动到A点时的机械能最小
C.若将小球在A点由静止开始释放,则小球沿ACB做圆周运动,到B点会有一定的速度
D.若将细线剪断,再将小球在A点以大小为的速度竖直向上抛出,则小球将不能到达B点
10.如图甲所示为一种测量带电微粒速率分布的实验装置.图中直径为D的竖直圆筒壁上有一竖直狭缝S,高度为h,宽度忽略不计.紧贴圆筒内壁固定有高度为H的半圆柱面收集板,用于收集带电微粒;板的一竖直边紧贴狭缝S,上边与狭缝S上端对齐,上边缘远离狭缝的顶点为P点,另有一距P点弧长为l的点Q,俯视图如图乙所示.圆筒内存在一竖直向下的匀强电场,电场强度为E.令圆筒以角速度ω绕中心轴顺时针转动,同时由微粒源产生的微粒沿水平方向、以不同的速率射入圆筒,微粒质量均为m,电荷量均为q,忽略微粒自身的重力及微粒间的相互作用.
(1)求Q点所在竖直线上收集到的微粒中,入射速率最大的微粒下落的距离;
(2)为了确保收集板任一竖直线上收集到的微粒速率相同,并且能收集到所有该速率的微粒,求圆筒转动角速度ω的取值范围.
参考答案与详细解析
1.B [解析] 河水在A、D两处近似做直线运动,在B、C处拐弯,河水所受的作用力指向轨迹凹侧,所以河水将受到B处河床对其的作用力,由牛顿第三定律知河水冲击最严重的是B处.
2.B [解析] 忽略月球自转的情况下,在月球表面行走时,巡视器受到的重力大小等于其受到的月球引力,而月球表面的重力加速度小于在地球表面的重力加速度,所以巡视器受到月球的引力小于1350 N,选项A错误;巡视器在AB段做曲线运动,即其速度方向发生变化,一定有加速度,选项B正确;根据平均速度公式=可知,平均速度方向与位移方向相同,由于在OA段、AB段的位移方向不同,则平均速度方向不同,选项C错误;由图可知OAB的轨迹长度大于从O到B的位移大小,选项D错误.
3.AD [解析] 将运动员从C到D的运动沿倾斜直滑道方向和垂直于倾斜直滑道方向分解,运动员在垂直于倾斜直滑道方向上做加速度与初速度方向相反的匀变速直线运动,在沿倾斜滑道方向上做匀加速直线运动,根据对称性可知,运动员运动至相对斜面最高点E所用的时间恰好为运动全程所用时间的一半,所以t1=t2,A正确,B错误;由于从C到E的时间和从E到D的时间相等,则CF和FD相当于连续相等时间内的两段位移,但因沿斜面方向的初速度不为零,所以>,C错误,D正确.
4.C [解析] 对人和车受力分析,如图所示,根据几何关系有FN==1500 N,根据牛顿第三定律可知,车对弯道的压力大小为1500 N,故A错误;由于不知道人的质量,所以无法确定人对车的压力大小,故B错误;根据牛顿第二定律可得mgtan θ=m=ma,解得r=67.5 m,a=13.33 m/s2,故C正确,D错误.
5.C [解析] 炮弹在最高点时,竖直方向的分速度为零,水平方向的分速度不为零,故炮弹在最高点时的速度不为零,A错误;在最高点时,炮弹受到空气阻力和重力作用,二力合力不为零,故加速度不为零,B错误;由于空气阻力恒做负功,所以炮弹飞行过程中机械能减少,因炮弹经过a、c两点时的重力势能相同,故炮弹经过a点时的动能大于经过c点时的动能,则经过a点时的速度大于经过c点时的速度,C正确;炮弹从O点到b点的过程中,在竖直方向上,受到重力和阻力沿竖直方向向下的分力,即mg+Ff1=may,解得ay=,从b点到d点的过程中,在竖直方向上,受到重力和阻力沿竖直方向向上的分力,即mg-Ff2=may',解得ay'=,故ay>ay',两个阶段的竖直位移大小相同,加速度越大,则所用时间越短,所以炮弹由O点运动到b点的时间小于由b点运动到d点的时间,故D错误.
6.B [解析] 4条水柱中,①中的水上升最高,则水在空中的运动时间最大,出射时的竖直分速度最大,但出射速度不一定最大,故A错误;②中的水的高度大于③中的水的高度,所以②中的水在空中运动的时间比③中的长,故B正确;在最高点时,水的速度只有水平方向的分量,而②中的水比③中的水水平速度小,所以在最高点时,②中的水比③中的水速度小,故C错误;水的射程为x=v0cos θ·t=v0cos θ·2=,当喷口的倾角为45°时,水的射程最远,故D错误.
7.C [解析] 在地面上做此实验,忽略空气阻力,小球受到重力和细绳拉力的作用,拉力始终和小球的速度垂直,不做功,重力会改变小球的速度大小;在“天宫”上,小球处于完全失重的状态,小球仅在细绳拉力作用下做匀速圆周运动,细绳拉力仍然不做功,A错误,C正确.在地面上,小球运动的速度大小改变,可知小球的向心加速度大小和细绳的拉力大小均发生改变;在“天宫”上,小球的向心加速度大小和细绳的拉力大小均不发生改变,B、D错误.
8.C [解析] A、B有相同的角速度,根据ω=,可得TA=TB,即A的周期等于B的周期,D错误;水平桌面光滑,所以杆对A的作用力提供了A做圆周运动的向心力,即FA=mAω2rA,杆对B的作用力提供了B做圆周运动的向心力,即FB=mBω2rB,联立解得FA=2FB,由牛顿第三定律可知,A对杆的作用力大小不等于B对杆的作用力大小,A错误;根据a=ω2r,可得aA∶aB=rA∶rB=1∶2,即A的向心加速度大小小于B的向心加速度大小,B错误;根据Ek=mv2=mω2r2,可得EkA∶EkB=(mA)∶(mB)=1∶1,即A的动能等于B的动能,C正确.
9.BD [解析] 小球受到竖直向下的重力mg和水平向右的电场力F=Eq=,小球所受的合力为F合==,设合力方向与电场线方向夹角为θ,有tan θ==,解得θ=60°,若将小球从A点由静止开始释放,则小球将沿合力方向做匀加速直线运动,C错误;若小球恰能在竖直平面内绕O点做匀速圆周运动,设它运动的最小速度为v,则由牛顿第二定律有F合=m,解得v=,A错误;小球运动过程中机械能的增加量等于除重力、弹力外其他力做的功,要想使机械能最小,电场力应做负功且做功最多,所以若小球在竖直平面内绕过O点做圆周运动,则小球运动到A点时,电场力做的负功最多,机械能最小,B正确;若将细线剪断,再将小球在A点以大小为的速度竖直向上抛出, 在竖直方向上小球做竖直上抛运动,在水平方向上小球做匀加速直线运动,当竖直方向上的位移为0时,所用时间t=,此过程的水平位移x=at2,其中a==g,联立解得x=d,由于x<2d,所以小球将不能到达B点,D正确.
10.(1) (2)<ω<
[解析] (1)Q点所在竖直线上收集到的微粒中,入射速率最大的微粒下落的过程中,圆筒转过的角度为θ==
对应的时间为t=
微粒下落的加速度为a=
下落的高度为y0=at2
联立解得y0=
(2)要确保收集板上任一竖直线上收集到的微粒速率相同,应控制圆筒不能转得太快,使圆筒转动一周时沿狭缝上端射入的微粒能越过收集板下边界,即微粒沿电场方向的位移y1=H时对应的运动时间t1<
其中y1=·
联立解得ω<
要确保收集板上收集到所有该速率的粒子,应控制圆筒不能转得太慢,使圆筒转动半周时沿狭缝下端射入的微粒不会越过收集板下边界,即微粒沿电场方向的位移y2=H-h时对应的时间t2>
其中y2=·
联立解得ω>
所以<ω<
因为H>h,所以<自动满足,结果合理.
专题一 力与运动 第3讲 力与曲线运动(A) -专项训练
1.[2024·温州模拟] 如图所示为某段河流,河水沿着河床做曲线运动.图中A、B、C、D四处中,受河水冲击最严重的是 ( )
A.A处 B.B处
C.C处 D.D处
2.[2024·金华模拟] 如图所示为“玉兔二号”巡视器在月球上从O处行走到B处的照片.轨迹OA段是直线,AB段是曲线,巡视器质量为135 kg,则巡视器 ( )
A.受到月球的引力为1350 N
B.在AB段运动时一定有加速度
C.在OA段与AB段的平均速度方向相同
D.从O到B的位移大小等于OAB的轨迹长度
3.(不定项)[2024·桐乡一中模拟] 芬兰小将拉林托以两跳240.9分的成绩在跳台滑雪世界杯芬兰站中获得冠军.如图所示是简化后的跳台滑雪的雪道示意图,拉林托从助滑雪道AB上由静止开始滑下,到达C点后水平飞出,落到倾斜直滑道上的D点,E是运动轨迹上的某一点,在该点拉林托的速度方向与直滑道CD平行.设拉林托从C到E与从E到D的运动时间分别为t1、t2,EF垂直于CD,忽略空气阻力,则( )
A.t1=t2
B.t1>t2
C.=
D.>
4.钢架雪车是一项精彩刺激的冬奥会比赛项目,运动员从起跑区推动雪车起跑后俯卧在雪车上,再经出发区、滑行区和减速区的一系列直道、弯道后到达终点,用时少者获胜.图甲是比赛中一运动员在滑行区某弯道上的照片.假设可视为质点的人和车的总质量m=90 kg,其在弯道上P处做水平面内的圆周运动的模型如图乙所示,车在P处既无侧移也无切向加速度,速率v=30 m/s,弯道表面与水平面成θ=53°角,不计摩擦力和空气阻力,重力加速度g取10 m/s2,sin 53°=0.8,cos 53°=0.6,则在P处 ( )
A.车对弯道的压力大小为900 N
B.人对车的压力大小为1500 N
C.人和车做圆周运动的半径为67.5 m
D.人和车的加速度大小为7.5 m/s2
5.[2024·舟山模拟] 由于空气阻力的影响,炮弹的实际飞行轨迹不是抛物线,而是“弹道曲线”,如图中实线所示.图中虚线为不考虑空气阻力情况下炮弹的理想运动轨迹,O、a、b、c、d为弹道曲线上的五点,其中O点为发射点,d点为落地点,b点为轨迹的最高点,a、c为运动过程中经过的离地面高度相等的两点.下列说法正确的是 ( )
A.到达b点时,炮弹的速度为零
B.到达b点时,炮弹的加速度为零
C.炮弹经过a点时的速度大于经过c点时的速度
D.炮弹由O点运动到b点的时间大于由b点运动到d点的时间
6.[2024·余姚模拟] 如图所示为西湖音乐喷泉某时刻的照片,水从喷口倾斜射出,空中呈现不同的抛物线,取其中4条抛物线,分别记作①②③④.空气阻力不计,下列说法正确的是 ( )
A.4条水柱中,①中的水上升最高,其出射速度最大
B.②中的水比③中的水在空中运动的时间长
C.在最高点时,②中的水比③中的水速度大
D.喷口的倾角越小,则水的射程越远
7.[2022·北京卷] 我国航天员在“天宫课堂”中演示了多种有趣的实验,提高了青少年科学探索的兴趣.某同学设计了如下实验:细绳一端固定,另一端系一小球,给小球一初速度使其在竖直平面内做圆周运动.无论在“天宫”还是在地面做此实验 ( )
A. 小球的速度大小均发生变化
B. 小球的向心加速度大小均发生变化
C. 细绳的拉力对小球均不做功
D. 细绳的拉力大小均发生变化
8.[2024·镇海中学模拟] 如图所示,轻杆两端分别固定着可以视为质点的小球A、B,放置在光滑水平桌面上,杆上O点处穿过一竖直转动轴,A、B的质量之比mA∶mB=4∶1,A、B到O点的距离之比rA∶rB=1∶2.当轻杆绕轴匀速转动时,下列说法正确的是 ( )
A.A对杆的作用力大小等于B对杆的作用力大小
B.A的向心加速度大小大于B的向心加速度大小
C.A的动能等于B的动能
D.A的周期小于B的周期
9.(不定项)如图所示,在地面上方的水平匀强电场中,一个质量为m、电荷量为+q的小球系在一根长为d的绝缘细线一端,可以在竖直平面内绕O点做圆周运动.AB为圆周的水平直径,CD为竖直直径.已知重力加速度为g,电场强度E=,下列说法正确的是( )
A.若小球恰能在竖直平面内绕O点做圆周运动,则它运动的最小速度为
B.若小球在竖直平面内绕O点做圆周运动,则小球运动到A点时的机械能最小
C.若将小球在A点由静止开始释放,则小球沿ACB做圆周运动,到B点会有一定的速度
D.若将细线剪断,再将小球在A点以大小为的速度竖直向上抛出,则小球将不能到达B点
10.如图甲所示为一种测量带电微粒速率分布的实验装置.图中直径为D的竖直圆筒壁上有一竖直狭缝S,高度为h,宽度忽略不计.紧贴圆筒内壁固定有高度为H的半圆柱面收集板,用于收集带电微粒;板的一竖直边紧贴狭缝S,上边与狭缝S上端对齐,上边缘远离狭缝的顶点为P点,另有一距P点弧长为l的点Q,俯视图如图乙所示.圆筒内存在一竖直向下的匀强电场,电场强度为E.令圆筒以角速度ω绕中心轴顺时针转动,同时由微粒源产生的微粒沿水平方向、以不同的速率射入圆筒,微粒质量均为m,电荷量均为q,忽略微粒自身的重力及微粒间的相互作用.
(1)求Q点所在竖直线上收集到的微粒中,入射速率最大的微粒下落的距离;
(2)为了确保收集板任一竖直线上收集到的微粒速率相同,并且能收集到所有该速率的微粒,求圆筒转动角速度ω的取值范围.
参考答案与详细解析
1.B [解析] 河水在A、D两处近似做直线运动,在B、C处拐弯,河水所受的作用力指向轨迹凹侧,所以河水将受到B处河床对其的作用力,由牛顿第三定律知河水冲击最严重的是B处.
2.B [解析] 忽略月球自转的情况下,在月球表面行走时,巡视器受到的重力大小等于其受到的月球引力,而月球表面的重力加速度小于在地球表面的重力加速度,所以巡视器受到月球的引力小于1350 N,选项A错误;巡视器在AB段做曲线运动,即其速度方向发生变化,一定有加速度,选项B正确;根据平均速度公式=可知,平均速度方向与位移方向相同,由于在OA段、AB段的位移方向不同,则平均速度方向不同,选项C错误;由图可知OAB的轨迹长度大于从O到B的位移大小,选项D错误.
3.AD [解析] 将运动员从C到D的运动沿倾斜直滑道方向和垂直于倾斜直滑道方向分解,运动员在垂直于倾斜直滑道方向上做加速度与初速度方向相反的匀变速直线运动,在沿倾斜滑道方向上做匀加速直线运动,根据对称性可知,运动员运动至相对斜面最高点E所用的时间恰好为运动全程所用时间的一半,所以t1=t2,A正确,B错误;由于从C到E的时间和从E到D的时间相等,则CF和FD相当于连续相等时间内的两段位移,但因沿斜面方向的初速度不为零,所以>,C错误,D正确.
4.C [解析] 对人和车受力分析,如图所示,根据几何关系有FN==1500 N,根据牛顿第三定律可知,车对弯道的压力大小为1500 N,故A错误;由于不知道人的质量,所以无法确定人对车的压力大小,故B错误;根据牛顿第二定律可得mgtan θ=m=ma,解得r=67.5 m,a=13.33 m/s2,故C正确,D错误.
5.C [解析] 炮弹在最高点时,竖直方向的分速度为零,水平方向的分速度不为零,故炮弹在最高点时的速度不为零,A错误;在最高点时,炮弹受到空气阻力和重力作用,二力合力不为零,故加速度不为零,B错误;由于空气阻力恒做负功,所以炮弹飞行过程中机械能减少,因炮弹经过a、c两点时的重力势能相同,故炮弹经过a点时的动能大于经过c点时的动能,则经过a点时的速度大于经过c点时的速度,C正确;炮弹从O点到b点的过程中,在竖直方向上,受到重力和阻力沿竖直方向向下的分力,即mg+Ff1=may,解得ay=,从b点到d点的过程中,在竖直方向上,受到重力和阻力沿竖直方向向上的分力,即mg-Ff2=may',解得ay'=,故ay>ay',两个阶段的竖直位移大小相同,加速度越大,则所用时间越短,所以炮弹由O点运动到b点的时间小于由b点运动到d点的时间,故D错误.
6.B [解析] 4条水柱中,①中的水上升最高,则水在空中的运动时间最大,出射时的竖直分速度最大,但出射速度不一定最大,故A错误;②中的水的高度大于③中的水的高度,所以②中的水在空中运动的时间比③中的长,故B正确;在最高点时,水的速度只有水平方向的分量,而②中的水比③中的水水平速度小,所以在最高点时,②中的水比③中的水速度小,故C错误;水的射程为x=v0cos θ·t=v0cos θ·2=,当喷口的倾角为45°时,水的射程最远,故D错误.
7.C [解析] 在地面上做此实验,忽略空气阻力,小球受到重力和细绳拉力的作用,拉力始终和小球的速度垂直,不做功,重力会改变小球的速度大小;在“天宫”上,小球处于完全失重的状态,小球仅在细绳拉力作用下做匀速圆周运动,细绳拉力仍然不做功,A错误,C正确.在地面上,小球运动的速度大小改变,可知小球的向心加速度大小和细绳的拉力大小均发生改变;在“天宫”上,小球的向心加速度大小和细绳的拉力大小均不发生改变,B、D错误.
8.C [解析] A、B有相同的角速度,根据ω=,可得TA=TB,即A的周期等于B的周期,D错误;水平桌面光滑,所以杆对A的作用力提供了A做圆周运动的向心力,即FA=mAω2rA,杆对B的作用力提供了B做圆周运动的向心力,即FB=mBω2rB,联立解得FA=2FB,由牛顿第三定律可知,A对杆的作用力大小不等于B对杆的作用力大小,A错误;根据a=ω2r,可得aA∶aB=rA∶rB=1∶2,即A的向心加速度大小小于B的向心加速度大小,B错误;根据Ek=mv2=mω2r2,可得EkA∶EkB=(mA)∶(mB)=1∶1,即A的动能等于B的动能,C正确.
9.BD [解析] 小球受到竖直向下的重力mg和水平向右的电场力F=Eq=,小球所受的合力为F合==,设合力方向与电场线方向夹角为θ,有tan θ==,解得θ=60°,若将小球从A点由静止开始释放,则小球将沿合力方向做匀加速直线运动,C错误;若小球恰能在竖直平面内绕O点做匀速圆周运动,设它运动的最小速度为v,则由牛顿第二定律有F合=m,解得v=,A错误;小球运动过程中机械能的增加量等于除重力、弹力外其他力做的功,要想使机械能最小,电场力应做负功且做功最多,所以若小球在竖直平面内绕过O点做圆周运动,则小球运动到A点时,电场力做的负功最多,机械能最小,B正确;若将细线剪断,再将小球在A点以大小为的速度竖直向上抛出, 在竖直方向上小球做竖直上抛运动,在水平方向上小球做匀加速直线运动,当竖直方向上的位移为0时,所用时间t=,此过程的水平位移x=at2,其中a==g,联立解得x=d,由于x<2d,所以小球将不能到达B点,D正确.
10.(1) (2)<ω<
[解析] (1)Q点所在竖直线上收集到的微粒中,入射速率最大的微粒下落的过程中,圆筒转过的角度为θ==
对应的时间为t=
微粒下落的加速度为a=
下落的高度为y0=at2
联立解得y0=
(2)要确保收集板上任一竖直线上收集到的微粒速率相同,应控制圆筒不能转得太快,使圆筒转动一周时沿狭缝上端射入的微粒能越过收集板下边界,即微粒沿电场方向的位移y1=H时对应的运动时间t1<
其中y1=·
联立解得ω<
要确保收集板上收集到所有该速率的粒子,应控制圆筒不能转得太慢,使圆筒转动半周时沿狭缝下端射入的微粒不会越过收集板下边界,即微粒沿电场方向的位移y2=H-h时对应的时间t2>
其中y2=·
联立解得ω>
所以<ω<
因为H>h,所以<自动满足,结果合理.
同课章节目录
