6.3三角形的中位线 同步练习题 (含答案) 北师大版八年级数学下册
文档属性
| 名称 | 6.3三角形的中位线 同步练习题 (含答案) 北师大版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 305.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-06 10:26:43 | ||
图片预览



文档简介
北师大版八年级数学下册《6.3三角形的中位线》同步练习题
一.选择题
1.已知等腰三角形的两条中位线的长分别为3和5,则此等腰三角形的周长为( )
A.22 B.26 C.22或26 D.13
2.如图,A,B两点被池塘隔开,在AB外选一点C,连接AC,BC,分别取AC,BC的中点D,E,连接DE.若测得DE=5,则AB的长为( )
A.5 B.8 C.10 D.无法确定
3.如图,△ABC中,AB=8,AD为∠BAC的外角平分线,且AD⊥CD于点D,E为BC的中点,若DE=10,则AC的长为( )
A.12 B.14 C.16 D.18
4.如图,四边形ABCD中,AD∥BC,AD=2,BC=5,点E,F分别是对角线AC,BD的中点,则EF的长为( )
A.1 B.1.5 C.2.5 D.3.5
5.如图,在四边形ABCD中,点E,F分别是边AB,AD的中点,连EF,若EF=2,CD=3,且EF⊥CD,则BC的长为( )
A.12 B.5 C.7 D.6
6.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )
A.5 B.10 C.15 D.20
7.如图,在△ABC中,AB=10,BC=6,点D为AB上一点,BC=BD,BE⊥CD于点E,点F为AC的中点,连接EF,则EF的长为( )
A.1 B.2 C.3 D.4
8.如图,Rt△ABC中,∠BAC=90°,AB=6,BC=10,AD、AE分别是其角平分线和中线,过点B作BG⊥AD于G,交AC于F,连接EG,则线段EG的长为( )
A. B.1 C. D.2
9.如图,矩形ABCD中,AB=2,BC=3,点P是BC边上任意一点,E,F,R分别是AP,RP,CD的中点,则EF的长为( )
A. B. C. D.
10.如图,小红作出了边长为1的第1个等边△A1B1C1,算出了等边△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2、B2、C2,作出了第2个等边△A2B2C2,算出了等边△A2B2C2的面积,用同样的方法,作出了第3个等边△A3B3C3,算出了等边△A3B3C3的面积…,由此可得,第n个等边△AnBn n的面积是( )
A. B.
C. D.
二.填空题
11.已知:三角形的各边分别为8cm、10cm和12cm,连接各边中点所成三角形的周长= .
12.如图,△ABC中,BD平分∠ABC,且AD⊥BD,E为AC的中点,AD=6cm,BD=8cm,BC=16cm,则DE的长为 cm.
13.如图,在△ABC中,D、E分别为AB、AC的中点,CF平分∠ACB,交DE于点F,若BC=10,AC=4,则DF的长为 .
14.如图,△ABC中,DE是BC的垂直平分线,CE是∠ACB的平分线,FG为△ACE的中位线,连DF,若∠DFG=108°,则∠AED= .
15.如图,△ABC中,∠ACB=90°,AB边上的高线CD与△ABC的两条角平分线AE,BF分别交于H,G两点,点P,Q分别为HE,GF的中点,连接PQ,若AC=4,BC=6,则PQ的长为 .
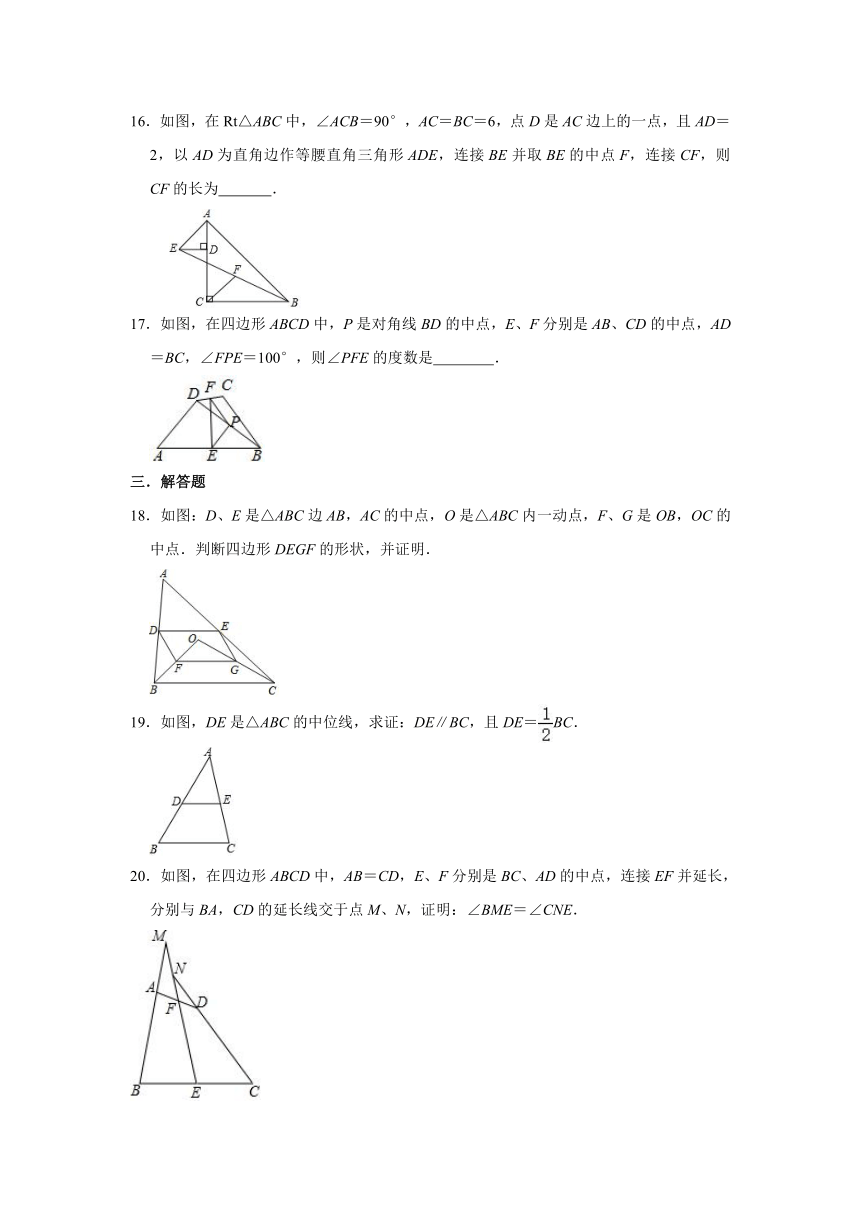
16.如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,点D是AC边上的一点,且AD=2,以AD为直角边作等腰直角三角形ADE,连接BE并取BE的中点F,连接CF,则CF的长为 .
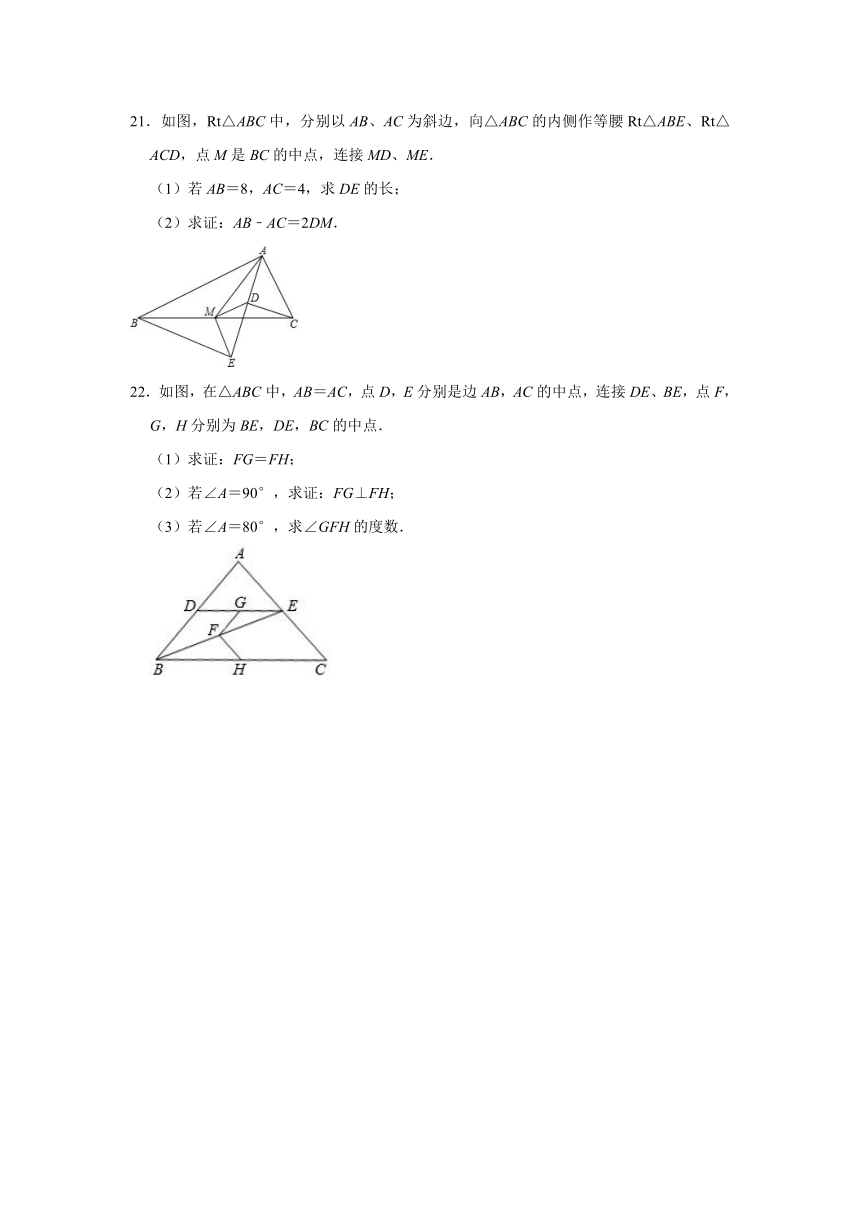
17.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠FPE=100°,则∠PFE的度数是 .
三.解答题
18.如图:D、E是△ABC边AB,AC的中点,O是△ABC内一动点,F、G是OB,OC的中点.判断四边形DEGF的形状,并证明.
19.如图,DE是△ABC的中位线,求证:DE∥BC,且DE=BC.
20.如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.
21.如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.
(1)若AB=8,AC=4,求DE的长;
(2)求证:AB﹣AC=2DM.
22.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.
参考答案
一.选择题
1.解:等腰三角形的两条中位线长分别为3和5,
根据三角形中位线定理可知,等腰三角形的两边长为6和10,
当腰为10时,则三边长为10,10,6时,周长为26;
当腰为6时,则三边长为6,6,10时,周长为22,
故选:C.
2.解:∵D,E分别为AC,BC的中点,
∴AB=2DE,
∵DE=5,
∴AB=10,
故选:C.
3.解:延长BA、CD交于点F,
在△ADF和△ADC中,
,
∴△ADF≌△ADC(ASA),
∴CD=DF,AC=AF,
∵CD=DF,CE=EB,
∴BF=2DE=20,
∴AF=BF﹣AB=20﹣8=12,
∴AC=AF=12,
故选:A.
4.解:∵取DC中点G,连结FG、EG,如图所示:
∵点E,F分别是对角线AC,BD的中点,
∴FG∥BC,EG∥AD,
∵AD∥BC,
∴EG∥BC,FG∥EG,
∴E、F、G三点共线,
∴FG是△BCD的中位线,
∴FG=BC=2.5,
∵AD∥BC,
∴EG∥AD,
∴EG是△ACD的中位线,
∴EG=AD=1,
∴EF=FG﹣EG=1.5.
故选:B.
5.解:连接BD,
∵点E,F分别是边AB,AD的中点,
∴BD=2EF=4,BD∥EF,
∵BD∥EF,EF⊥CD,
∴∠BDC=90°,
∴BC==5,
故选:B.
6.解:∵D、E分别是△ABC的边BC、AB的中点,
∴DE=AC,
同理 EF=BC,DF=AB,
∴C△DEF=DE+EF+DF=(AC+BC+AB)=×20=10.
故选:B.
7.解:BD=BC=6,
∴AD=AB﹣BD=4,
∵BC=BD,BE⊥CD,
∴CE=ED,又CF=FA,
∴EF=AD=2,
故选:B.
8.解:Rt△ABC中,∠BAC=90°,AB=6,BC=10,
∴AC=8,
∵BG⊥AD,AD平分∠BAC,
∴AB=AF=6,BG=FG,
∴CF=2,
∵AE是△ABC的中线,
∴BE=CE,
∴EG=CF=1,
故选:B.
9.解:连接AR,
∵四边形ABCD是矩形,
∴∠D=90°,AB=DC=2,
∵R是CD的中点,
∴DR=1,
由勾股定理得,AR==,
∵E、F分别是PA、PR的中点,
∴EF是△APR的中位线,
∴EF=AR=×=.
故选:B.
10.解:等边△A1B1C1的面积为:××12=,
∵△A1B1C1三边的中点为A2,B2,C2,
∴A2B2是△A1B1C1的中位线,
∴A2B2∥A1B1,A2B2=A1B1,
∴△A2B2C2的面积:△A1B1C1的面积=1:4,
∴等边△A2B2C2的面积为:×=,
同理可知,等边△A3B3C3的面积:等边△A2B2C2的面积=1:4,
∴等边△A3B3C3的面积为:×=,…,
依此类推第n个等边△AnBn n的面积是:=×()n﹣1,
故选:C.
二.填空题
11.解:如图,D,E,F分别是△ABC的三边的中点,
则DE=AC,DF=BC,EF=AB,
∴△DEF的周长=DE+DF+EF=(AC+BC+AB)=×(8+10+12)cm=15cm.
答:以各边中点为顶点的三角形的周长是15cm,
故答案为:15cm.
12.解:如图,延长AD交BC于F,
∵BD平分∠ABC,
∴∠ABD=∠FBD,
∵AD⊥BD,
∴∠BDA=∠BDF=90°,AB===10(cm),
在△BDF和△BDA中,,
∴△BDF≌△BDA(ASA),
∴DF=AD,FB=AB=10cm,
∴CF=BC﹣FB=16﹣10=6cm,
又∵点E为AC的中点,
∴DE是△ACF的中位线,
∴DE=CF=3cm.
故答案为:3.
13.解:∵D、E分别为AB、AC的中点,BC=10,AC=4,
∴DE=BC=5,DE∥BC,EC=AC=2,
∴∠EFC=∠BCF,
∵CF平分∠ACB,
∴∠ECF=∠BCF,
∴∠EFC=∠ECF,
∴EF=EC=2,
∴DF=DE﹣EF=5﹣2=3,
故答案为:3.
14.解:∵DE是BC的垂直平分线,
∴BE=CE,
∴∠EBC=∠ECB,
设∠EBC=∠ECB=x,
∴∠AEC=∠EBC+∠ECB=2x,
∵CE平分∠ACB,
∴∠BCE=∠ACE=x,
∵FG是△ACE的中位线,
∴FG∥AC,
∴∠EFG=∠ACE=x,
∵D为BC的中点,F为CE的中点,
∴DF∥AB,
∴∠EFD=∠AEF=2x,
∵∠DFG=∠GFE+∠EFD=x+2x=3x,
∴3x=108°,
∴x=36°,
∴∠AED=∠AEC+∠CED=2x+90°﹣x=90°+x=90°+36°=126°,
故答案为:126°.
15.解:延长CP交AB于K,延长CQ交AB于L,
△ABC中,∠ACB=90°,
由勾股定理得:AB===2,
∵BF是∠ABC的平分线,
∴∠ABF=∠CBF,
又∵CD⊥AB,
∴∠CGF=∠BGD=90°﹣∠ABF=90°﹣∠CBF=∠CFB,
∴CG=CF.
又∵Q是GF的中点,
∴CQ⊥GF,
∴∠CQB=∠LQB=90°,
∴∠BCQ=∠BLQ,
∴BL=BC=6,
∴CQ=LQ,
同理得:CE=CH,
∵P是EH的中点,
∴CP⊥EH,
∴AP⊥CK,同理得AK=AC=4,CP=PK,
∵CP=PK,CQ=LQ,
∴PQ=LK=(BL+AK﹣AB)=(6+4﹣2)=5﹣;
故答案为:5﹣.
16.解:延长AE、BC交于点H,
∵△ADE是等腰直角三角形,
∴∠HAC=45°,AE=AD=2,
∴CH=AC=BC,AH=AC=6,
∴EH=AH﹣AE=4,
∵BC=CH,BF=FE,
∴FC=EH=2,
故答案为:2.
17.解:∵P是对角线BD的中点,E是AB的中点,
∴EP=AD,
同理,FP=BC,
∵AD=BC,
∴PE=PF,
∵∠FPE=100°,
∴∠PFE=40°,
故答案为:40°.
三.解答题
18.解:四边形DEGF是平行四边形,
理由如下:∵D、E是△ABC边AB,AC的中点,
∴DE=BC,DE∥BC,
∵F、G是OB,OC的中点,
∴FG=BC,FG∥BC,
∴DE=FG,DE∥FG,
∴四边形DEGF是平行四边形.
19.证明:延长DE到Q,使DE=EQ,连接CQ,
∵AE=EC,∠AED=∠CEQ,DE=EQ,
∴△ADE≌△CQE,
∴AD=CQ,∠A=∠ACQ,
∴AB∥CQ,
∵AD=BD,
∴BD=CQ,
∴四边形DBCQ是平行四边形,
∴DQ=BC,DQ∥BC,
∴DE∥BC,DE=BC.
20.证明:连接BD,取BD的中点H,连接HE,HF,
∵E、F分别是BC、AD的中点,
∴FH∥BM,FH=AB,EH∥CN,EH=CD,
∴∠BME=∠HFE,∠CNE=∠HEF,
∵AB=CD,
∴FH=EH,
∴∠HFE=∠HEF,
∴∠BME=∠CNE.
21.解:(1)直角△ABE中,AE=AB=4,
在直角△ACD中,AD=AC=2,
则DE=AE﹣AD=4﹣2=2;
(2)延长CD交AB于点F.
在△ADF和△ADC中,
,
∴△ADF≌△ADC(ASA),
∴AC=AF,CD=DF,
又∵M是BC的中点,
∴DM是△CBF的中位线,
∴DM=BF=(AB﹣AF)=(AB﹣AC),
∴AB﹣AC=2DM.
22.(1)证明:∵AB=AC,点D,E分别是边AB,AC的中点
∴BD=EC
∵点F,G,H分别为BE,DE,BC的中点
∴FG∥BD,GF=
FH∥EC,FH=
∴FG=FH;
(2)证明:由(1)FG∥BD
又∵∠A=90°
∴FG⊥AC
∵FH∥EC
∴FG⊥FH;
(3)解:延长FG交AC于点K,
∵FG∥BD,∠A=80°
∴∠FKC=∠A=80°
∵FH∥EC
∴∠GFH=180°﹣∠FKC=100°
一.选择题
1.已知等腰三角形的两条中位线的长分别为3和5,则此等腰三角形的周长为( )
A.22 B.26 C.22或26 D.13
2.如图,A,B两点被池塘隔开,在AB外选一点C,连接AC,BC,分别取AC,BC的中点D,E,连接DE.若测得DE=5,则AB的长为( )
A.5 B.8 C.10 D.无法确定
3.如图,△ABC中,AB=8,AD为∠BAC的外角平分线,且AD⊥CD于点D,E为BC的中点,若DE=10,则AC的长为( )
A.12 B.14 C.16 D.18
4.如图,四边形ABCD中,AD∥BC,AD=2,BC=5,点E,F分别是对角线AC,BD的中点,则EF的长为( )
A.1 B.1.5 C.2.5 D.3.5
5.如图,在四边形ABCD中,点E,F分别是边AB,AD的中点,连EF,若EF=2,CD=3,且EF⊥CD,则BC的长为( )
A.12 B.5 C.7 D.6
6.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )
A.5 B.10 C.15 D.20
7.如图,在△ABC中,AB=10,BC=6,点D为AB上一点,BC=BD,BE⊥CD于点E,点F为AC的中点,连接EF,则EF的长为( )
A.1 B.2 C.3 D.4
8.如图,Rt△ABC中,∠BAC=90°,AB=6,BC=10,AD、AE分别是其角平分线和中线,过点B作BG⊥AD于G,交AC于F,连接EG,则线段EG的长为( )
A. B.1 C. D.2
9.如图,矩形ABCD中,AB=2,BC=3,点P是BC边上任意一点,E,F,R分别是AP,RP,CD的中点,则EF的长为( )
A. B. C. D.
10.如图,小红作出了边长为1的第1个等边△A1B1C1,算出了等边△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2、B2、C2,作出了第2个等边△A2B2C2,算出了等边△A2B2C2的面积,用同样的方法,作出了第3个等边△A3B3C3,算出了等边△A3B3C3的面积…,由此可得,第n个等边△AnBn n的面积是( )
A. B.
C. D.
二.填空题
11.已知:三角形的各边分别为8cm、10cm和12cm,连接各边中点所成三角形的周长= .
12.如图,△ABC中,BD平分∠ABC,且AD⊥BD,E为AC的中点,AD=6cm,BD=8cm,BC=16cm,则DE的长为 cm.
13.如图,在△ABC中,D、E分别为AB、AC的中点,CF平分∠ACB,交DE于点F,若BC=10,AC=4,则DF的长为 .
14.如图,△ABC中,DE是BC的垂直平分线,CE是∠ACB的平分线,FG为△ACE的中位线,连DF,若∠DFG=108°,则∠AED= .
15.如图,△ABC中,∠ACB=90°,AB边上的高线CD与△ABC的两条角平分线AE,BF分别交于H,G两点,点P,Q分别为HE,GF的中点,连接PQ,若AC=4,BC=6,则PQ的长为 .
16.如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,点D是AC边上的一点,且AD=2,以AD为直角边作等腰直角三角形ADE,连接BE并取BE的中点F,连接CF,则CF的长为 .
17.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠FPE=100°,则∠PFE的度数是 .
三.解答题
18.如图:D、E是△ABC边AB,AC的中点,O是△ABC内一动点,F、G是OB,OC的中点.判断四边形DEGF的形状,并证明.
19.如图,DE是△ABC的中位线,求证:DE∥BC,且DE=BC.
20.如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.
21.如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.
(1)若AB=8,AC=4,求DE的长;
(2)求证:AB﹣AC=2DM.
22.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.
参考答案
一.选择题
1.解:等腰三角形的两条中位线长分别为3和5,
根据三角形中位线定理可知,等腰三角形的两边长为6和10,
当腰为10时,则三边长为10,10,6时,周长为26;
当腰为6时,则三边长为6,6,10时,周长为22,
故选:C.
2.解:∵D,E分别为AC,BC的中点,
∴AB=2DE,
∵DE=5,
∴AB=10,
故选:C.
3.解:延长BA、CD交于点F,
在△ADF和△ADC中,
,
∴△ADF≌△ADC(ASA),
∴CD=DF,AC=AF,
∵CD=DF,CE=EB,
∴BF=2DE=20,
∴AF=BF﹣AB=20﹣8=12,
∴AC=AF=12,
故选:A.
4.解:∵取DC中点G,连结FG、EG,如图所示:
∵点E,F分别是对角线AC,BD的中点,
∴FG∥BC,EG∥AD,
∵AD∥BC,
∴EG∥BC,FG∥EG,
∴E、F、G三点共线,
∴FG是△BCD的中位线,
∴FG=BC=2.5,
∵AD∥BC,
∴EG∥AD,
∴EG是△ACD的中位线,
∴EG=AD=1,
∴EF=FG﹣EG=1.5.
故选:B.
5.解:连接BD,
∵点E,F分别是边AB,AD的中点,
∴BD=2EF=4,BD∥EF,
∵BD∥EF,EF⊥CD,
∴∠BDC=90°,
∴BC==5,
故选:B.
6.解:∵D、E分别是△ABC的边BC、AB的中点,
∴DE=AC,
同理 EF=BC,DF=AB,
∴C△DEF=DE+EF+DF=(AC+BC+AB)=×20=10.
故选:B.
7.解:BD=BC=6,
∴AD=AB﹣BD=4,
∵BC=BD,BE⊥CD,
∴CE=ED,又CF=FA,
∴EF=AD=2,
故选:B.
8.解:Rt△ABC中,∠BAC=90°,AB=6,BC=10,
∴AC=8,
∵BG⊥AD,AD平分∠BAC,
∴AB=AF=6,BG=FG,
∴CF=2,
∵AE是△ABC的中线,
∴BE=CE,
∴EG=CF=1,
故选:B.
9.解:连接AR,
∵四边形ABCD是矩形,
∴∠D=90°,AB=DC=2,
∵R是CD的中点,
∴DR=1,
由勾股定理得,AR==,
∵E、F分别是PA、PR的中点,
∴EF是△APR的中位线,
∴EF=AR=×=.
故选:B.
10.解:等边△A1B1C1的面积为:××12=,
∵△A1B1C1三边的中点为A2,B2,C2,
∴A2B2是△A1B1C1的中位线,
∴A2B2∥A1B1,A2B2=A1B1,
∴△A2B2C2的面积:△A1B1C1的面积=1:4,
∴等边△A2B2C2的面积为:×=,
同理可知,等边△A3B3C3的面积:等边△A2B2C2的面积=1:4,
∴等边△A3B3C3的面积为:×=,…,
依此类推第n个等边△AnBn n的面积是:=×()n﹣1,
故选:C.
二.填空题
11.解:如图,D,E,F分别是△ABC的三边的中点,
则DE=AC,DF=BC,EF=AB,
∴△DEF的周长=DE+DF+EF=(AC+BC+AB)=×(8+10+12)cm=15cm.
答:以各边中点为顶点的三角形的周长是15cm,
故答案为:15cm.
12.解:如图,延长AD交BC于F,
∵BD平分∠ABC,
∴∠ABD=∠FBD,
∵AD⊥BD,
∴∠BDA=∠BDF=90°,AB===10(cm),
在△BDF和△BDA中,,
∴△BDF≌△BDA(ASA),
∴DF=AD,FB=AB=10cm,
∴CF=BC﹣FB=16﹣10=6cm,
又∵点E为AC的中点,
∴DE是△ACF的中位线,
∴DE=CF=3cm.
故答案为:3.
13.解:∵D、E分别为AB、AC的中点,BC=10,AC=4,
∴DE=BC=5,DE∥BC,EC=AC=2,
∴∠EFC=∠BCF,
∵CF平分∠ACB,
∴∠ECF=∠BCF,
∴∠EFC=∠ECF,
∴EF=EC=2,
∴DF=DE﹣EF=5﹣2=3,
故答案为:3.
14.解:∵DE是BC的垂直平分线,
∴BE=CE,
∴∠EBC=∠ECB,
设∠EBC=∠ECB=x,
∴∠AEC=∠EBC+∠ECB=2x,
∵CE平分∠ACB,
∴∠BCE=∠ACE=x,
∵FG是△ACE的中位线,
∴FG∥AC,
∴∠EFG=∠ACE=x,
∵D为BC的中点,F为CE的中点,
∴DF∥AB,
∴∠EFD=∠AEF=2x,
∵∠DFG=∠GFE+∠EFD=x+2x=3x,
∴3x=108°,
∴x=36°,
∴∠AED=∠AEC+∠CED=2x+90°﹣x=90°+x=90°+36°=126°,
故答案为:126°.
15.解:延长CP交AB于K,延长CQ交AB于L,
△ABC中,∠ACB=90°,
由勾股定理得:AB===2,
∵BF是∠ABC的平分线,
∴∠ABF=∠CBF,
又∵CD⊥AB,
∴∠CGF=∠BGD=90°﹣∠ABF=90°﹣∠CBF=∠CFB,
∴CG=CF.
又∵Q是GF的中点,
∴CQ⊥GF,
∴∠CQB=∠LQB=90°,
∴∠BCQ=∠BLQ,
∴BL=BC=6,
∴CQ=LQ,
同理得:CE=CH,
∵P是EH的中点,
∴CP⊥EH,
∴AP⊥CK,同理得AK=AC=4,CP=PK,
∵CP=PK,CQ=LQ,
∴PQ=LK=(BL+AK﹣AB)=(6+4﹣2)=5﹣;
故答案为:5﹣.
16.解:延长AE、BC交于点H,
∵△ADE是等腰直角三角形,
∴∠HAC=45°,AE=AD=2,
∴CH=AC=BC,AH=AC=6,
∴EH=AH﹣AE=4,
∵BC=CH,BF=FE,
∴FC=EH=2,
故答案为:2.
17.解:∵P是对角线BD的中点,E是AB的中点,
∴EP=AD,
同理,FP=BC,
∵AD=BC,
∴PE=PF,
∵∠FPE=100°,
∴∠PFE=40°,
故答案为:40°.
三.解答题
18.解:四边形DEGF是平行四边形,
理由如下:∵D、E是△ABC边AB,AC的中点,
∴DE=BC,DE∥BC,
∵F、G是OB,OC的中点,
∴FG=BC,FG∥BC,
∴DE=FG,DE∥FG,
∴四边形DEGF是平行四边形.
19.证明:延长DE到Q,使DE=EQ,连接CQ,
∵AE=EC,∠AED=∠CEQ,DE=EQ,
∴△ADE≌△CQE,
∴AD=CQ,∠A=∠ACQ,
∴AB∥CQ,
∵AD=BD,
∴BD=CQ,
∴四边形DBCQ是平行四边形,
∴DQ=BC,DQ∥BC,
∴DE∥BC,DE=BC.
20.证明:连接BD,取BD的中点H,连接HE,HF,
∵E、F分别是BC、AD的中点,
∴FH∥BM,FH=AB,EH∥CN,EH=CD,
∴∠BME=∠HFE,∠CNE=∠HEF,
∵AB=CD,
∴FH=EH,
∴∠HFE=∠HEF,
∴∠BME=∠CNE.
21.解:(1)直角△ABE中,AE=AB=4,
在直角△ACD中,AD=AC=2,
则DE=AE﹣AD=4﹣2=2;
(2)延长CD交AB于点F.
在△ADF和△ADC中,
,
∴△ADF≌△ADC(ASA),
∴AC=AF,CD=DF,
又∵M是BC的中点,
∴DM是△CBF的中位线,
∴DM=BF=(AB﹣AF)=(AB﹣AC),
∴AB﹣AC=2DM.
22.(1)证明:∵AB=AC,点D,E分别是边AB,AC的中点
∴BD=EC
∵点F,G,H分别为BE,DE,BC的中点
∴FG∥BD,GF=
FH∥EC,FH=
∴FG=FH;
(2)证明:由(1)FG∥BD
又∵∠A=90°
∴FG⊥AC
∵FH∥EC
∴FG⊥FH;
(3)解:延长FG交AC于点K,
∵FG∥BD,∠A=80°
∴∠FKC=∠A=80°
∵FH∥EC
∴∠GFH=180°﹣∠FKC=100°
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
