2025届高考物理二轮复习:微专题1 传送带模型综合问题 理-专项训练 (含解析)
文档属性
| 名称 | 2025届高考物理二轮复习:微专题1 传送带模型综合问题 理-专项训练 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 155.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-05 12:52:15 | ||
图片预览


文档简介
2025届高考物理二轮复习
微专题1 传送带模型综合问题 理-专项训练
1.(不定项)[2022·广东卷] 如图所示,载有防疫物资的无人驾驶小车,在水平MN段以恒定功率200 W、速度5 m/s匀速行驶,在斜坡PQ段以恒定功率570 W、速度2 m/s匀速行驶,已知小车总质量为50 kg,MN=PQ=20 m,PQ段的倾角为30°,重力加速度g取10 m/s2,不计空气阻力.下列说法正确的有 ( )
A.从M到N,小车牵引力大小为40 N
B.从M到N,小车克服摩擦力做功800 J
C.从P到Q,小车重力势能增加1×104 J
D.从P到Q,小车克服摩擦力做功700 J
2.如图所示为低空跳伞极限运动表演,运动员从离地350 m高的桥面一跃而下,实现了自然奇观与极限运动的完美结合.假设质量为m的跳伞运动员由静止开始下落,在打开伞之前受恒定阻力作用,下落的加速度为g(g为重力加速度),则在运动员下落h高度的过程中,下列说法正确的是 ( )
A.运动员重力做功为mgh
B.运动员克服阻力做功为mgh
C.运动员的动能增加了mgh
D.运动员的机械能减少了mgh
3.如图所示,轻弹簧上端固定,下端拴着一带正电的小球Q,Q在A处时弹簧处于原长状态,Q可在C处静止.当将另一带正电的小球q固定在C正下方某处时,Q可在B处静止.在有小球q的情况下,将Q从A处由静止释放,则Q从A运动到C处的过程中( )
A.Q运动到C处时速率最大
B.Q、q两球组成的系统机械能不断增大
C.Q的机械能不断增大
D.Q的加速度先减小后增大
4.(不定项)如图所示,一小物块由静止开始沿倾角为53°的斜面向下滑动,最后停在水平地面上.斜面和地面平滑连接,且物块与斜面间、物块与地面间的动摩擦因数均为,取地面为零势能面,已知sin 53°=0.8,cos 53°=0.6.该过程中,物块的机械能E、重力势能Ep、动能Ek、摩擦产生的热量Q与水平位移x的关系图像可能正确的是 ( )
A
B
C
D
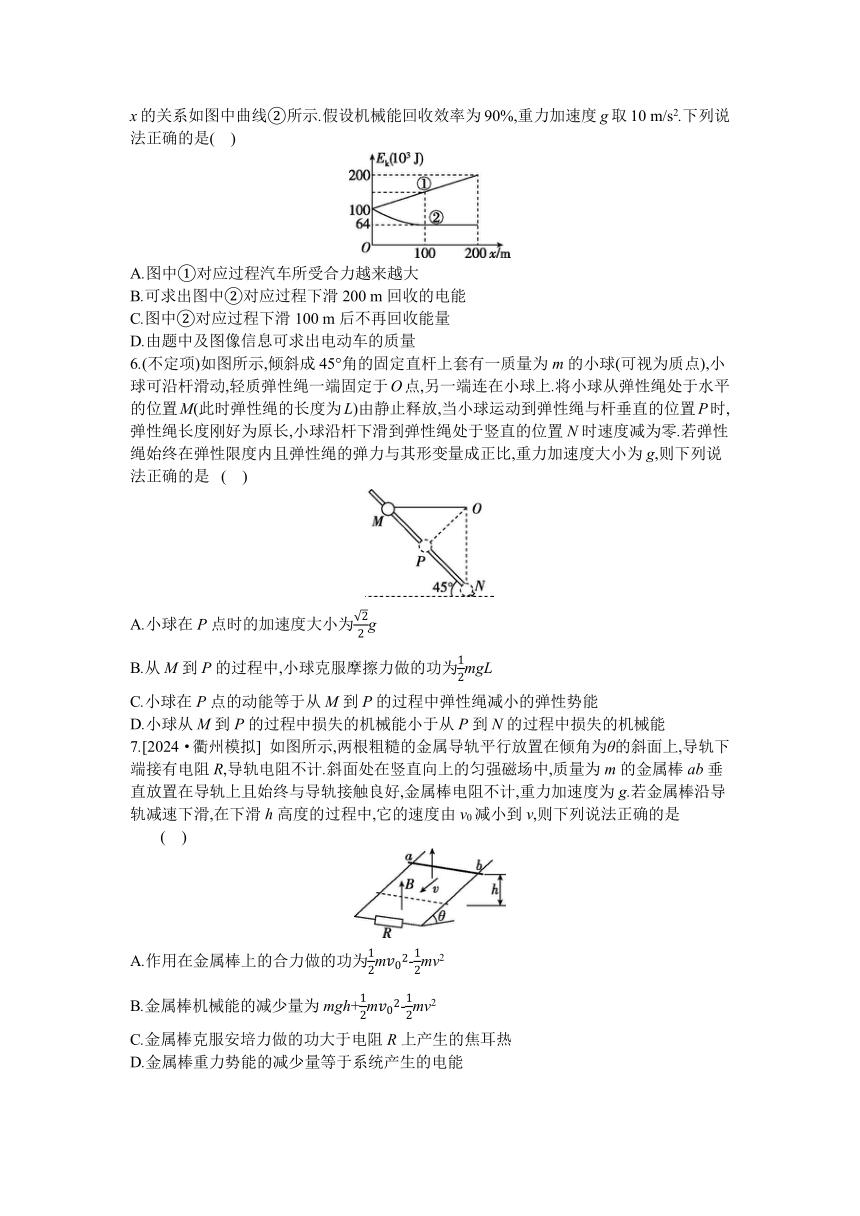
5.电动车配有把机械能转化为电能的“能量回收”装置.某次测试中电动车沿倾角为15°的斜坡向下运动,初动能为1.0×105 J.第一次让车无动力自由滑行,其动能Ek与位移x的关系如图中直线①所示;第二次让车无动力并开启“能量回收”装置滑行,其动能Ek与位移x的关系如图中曲线②所示.假设机械能回收效率为90%,重力加速度g取10 m/s2.下列说法正确的是( )
A.图中①对应过程汽车所受合力越来越大
B.可求出图中②对应过程下滑200 m回收的电能
C.图中②对应过程下滑100 m后不再回收能量
D.由题中及图像信息可求出电动车的质量
6.(不定项)如图所示,倾斜成45°角的固定直杆上套有一质量为m的小球(可视为质点),小球可沿杆滑动,轻质弹性绳一端固定于O点,另一端连在小球上.将小球从弹性绳处于水平的位置M(此时弹性绳的长度为L)由静止释放,当小球运动到弹性绳与杆垂直的位置P时,弹性绳长度刚好为原长,小球沿杆下滑到弹性绳处于竖直的位置N时速度减为零.若弹性绳始终在弹性限度内且弹性绳的弹力与其形变量成正比,重力加速度大小为g,则下列说法正确的是 ( )
A.小球在P点时的加速度大小为g
B.从M到P的过程中,小球克服摩擦力做的功为mgL
C.小球在P点的动能等于从M到P的过程中弹性绳减小的弹性势能
D.小球从M到P的过程中损失的机械能小于从P到N的过程中损失的机械能
7.[2024·衢州模拟] 如图所示,两根粗糙的金属导轨平行放置在倾角为θ的斜面上,导轨下端接有电阻R,导轨电阻不计.斜面处在竖直向上的匀强磁场中,质量为m的金属棒ab垂直放置在导轨上且始终与导轨接触良好,金属棒电阻不计,重力加速度为g.若金属棒沿导轨减速下滑,在下滑h高度的过程中,它的速度由v0减小到v,则下列说法正确的是 ( )
A.作用在金属棒上的合力做的功为m-mv2
B.金属棒机械能的减少量为mgh+m-mv2
C.金属棒克服安培力做的功大于电阻R上产生的焦耳热
D.金属棒重力势能的减少量等于系统产生的电能
8.如图所示,左侧光滑曲面轨道与右侧倾角α=37°的斜面在底部平滑连接且均固定在光滑水平地面上,质量为m的小滑块A从斜面上离斜面底边高为2H处由静止释放,经过斜面与水平地面交接处时无机械能损失,在水平地面上与一质量为m的静止小滑块B发生正碰并结合为一个整体(A、B完全相同),一起滑上左侧曲面轨道,再从曲面轨道滑回斜面,滑块第一次沿斜面上滑的最大高度为H,多次往复运动.不计空气阻力,重力加速度为g,sin 37°=0.6,cos 37°=0.8.求:
(1)滑块与斜面间的动摩擦因数μ;
(2)滑块第一次滑下斜面的时间t1与第一次滑上斜面的时间t2之比;
(3)滑块最终静止,整个系统由于摩擦产生的热量Q.
9.[2024·温岭中学模拟] 如图所示,水平轨道左端与长L=1.25 m的水平传送带相接,传送带逆时针匀速运动的速度v0=1 m/s.轻弹簧右端固定在光滑水平轨道上,弹簧处于自然状态.现用质量m=0.1 kg的小物块(视为质点)将弹簧压缩后由静止释放,到达水平传送带左端B点后,立即沿切线进入竖直固定的光滑半圆轨道最高点并恰好做圆周运动,经圆周最低点C后滑上质量为M=0.9 kg的长木板上,竖直半圆轨道的半径R=0.4 m,物块与传送带间的动摩擦因数μ1=0.8,物块与木板间的动摩擦因数μ2=0.25.g取10 m/s2.
(1)求物块到达B点时的速度vB的大小;
(2)求弹簧被压缩时的弹性势能Ep;
(3)要使小物块恰好不会从长木板上掉下,求木板长度s与木板和地面之间的动摩擦因数μ3的关系(设最大静摩擦力等于滑动摩擦力).
参考答案与详细解析
1.ABD [解析] 匀速时F牵=Ff,在MN段F牵==40 N,故A正确;W克f=Ff=800 J,B正确;从P到Q,ΔEp=mgΔh,ΔEp=5×103 J,故C错误;从P到Q,F牵'==285 N,F牵'=Ff'+mgsin θ,解得Ff'=35 N,W克f'=Ff'=700 J,D正确.
2.C [解析] 运动员下落h高度,则重力做功为WG=mgh,选项A错误;根据牛顿第二定律得mg-Ff=ma,其中a=g,解得Ff=mg,则运动员克服阻力做功为W克f=Ffh=mgh,选项B错误;运动员的动能增加量等于合外力做的功,则ΔEk=mah=mgh,选项C正确;运动员的机械能减少量等于克服阻力做的功,即ΔE=W克f=mgh,选项D错误.
3.D [解析] 当小球q固定在C正下方某处时,Q在B处时所受的合力为零,在此处时速率最大,故A错误;Q的机械能E等于Q的动能与重力势能之和,由功能关系有ΔE=W弹+W电,Q从A处运动到C处的过程中,由于弹簧从原长一直在伸长,故弹簧的弹力一直做负功,即W弹<0,且库仑力也一直做负功,即W电<0,则ΔE<0,即Q的机械能不断减小,故C错误;因小球q固定不动,则其机械能不变,因Q的机械能不断变小,故Q、q两球组成的系统机械能不断减小,故B错误;Q在B处时加速度为零,则Q从A处运动到B的过程中,加速度一直减小到零,而Q从B处运动到C处的过程中,加速度反向增大,故D正确.
4.BD [解析] 设O点到斜面底端的距离为x0,物块释放点的高度为h,物块从释放到停止运动的过程中,当水平位移x≤x0时,克服摩擦力做功W克f=μmgcos 53°·=μmgx,当x>x0时,克服摩擦力做功W克f=μmgcos 53°·+μmg·(x-x0)=μmgx,所以全程都有W克f=μmgx=mgx,根据功能关系可知摩擦产生的热量Q=W克f=μmgx,而物块在该过程中机械能的减少量始终等于克服摩擦力所做的功,则物块的机械能E=mgh-mgx,所以E-x图像是纵轴截距为mgh、斜率为-mg的倾斜直线,而其Q-x图像是过原点、斜率为mg的倾斜直线,故A错误,D正确;物块的重力势能Ep=mgh-mgtan 53°·x=mgh-mgx,所以Ep-x图像是纵轴截距为mgh、斜率为-mg的倾斜直线,且当x>x0时,重力势能始终为0,故B正确;物块从最高点下滑至斜面最低点的过程中,物块的动能Ek1=mgxtan 53°-μmgcos 53°·=mgx(x≤x0),当物块下滑至斜面底端时,其动能Ek1=mgx0,此后在水平面上克服摩擦力做功,物块的动能Ek2=mgx0-μmg(x-x0)=mgx0-mgx(x0≤x≤2x0),所以动能达到最大值前,Ek-x图像是过原点的倾斜直线,斜率为mg,动能达到最大后,Ek-x图像仍是倾斜直线,斜率为-mg,图像具有对称性,故C错误.
5.B [解析] 由动能定理得F合x=ΔEk,故Ek-x图像的斜率表示合外力,由图像可知,图中①对应过程汽车所受合力不变,F合= N=500 N,故A错误;由图中①可知,汽车自由下滑200 m过程,有WG+Wf=×103 J,由图中②可知,开启能量回收模式下滑200 m过程,有WG+Wf+WF=×103 J,则回收的电能为E=-WF×90%=1.224×105 J,故B正确;图中②对应过程下滑100 m后动能不变,但是重力势能减少,机械能减少,所以还是继续回收能量,故C错误;由图中①可知,F合=mgsin 15°-μmgcos 15°=500 N,由于不知道车与斜坡间的动摩擦因数,故无法由题中及图像信息求出电动车的质量,故D错误.
6.BCD [解析] 根据几何关系可知OM与ON长度相等,则小球在M处和在N处时弹性绳的弹性势能相等,小球从M到N的过程中,由动能定理有mgL-W克f=0,说明小球运动过程中受到摩擦力的作用,小球在P点时,由牛顿第二定律可知,其加速度a=gsin 45°-7.B [解析] 由动能定理得,作用在金属棒上的合力做的功为W=mv2-m,故A错误;金属棒下滑过程中,重力势能减少了mgh,动能减少了ΔEk=m-mv2,所以金属棒机械能的减少量为ΔE=mgh+m-mv2,故B正确;设金属棒下滑过程中,因摩擦产生的热为Q1,系统产生的电能为Q2,根据能量守恒定律有mgh+m-mv2=Q1+Q2,则Q2=mgh+m-mv2-Q1,因不能确定动能减少量和摩擦产生的热的关系,所以不能确定金属棒重力势能的减少量和系统产生的电能的关系,故D错误;由功能关系可知,金属棒克服安培力做的功等于电路中产生的焦耳热,由于导轨和金属棒的电阻都不计,则电路中只有电阻R上会产生焦耳热,所以金属棒克服安培力做的功等于电阻R上产生的焦耳热,故C错误.
8.(1)0.3 (2)14∶3 (3)1.4 mgH
[解析] (1)当滑块A由斜面滑到水平面时,由能量守恒定律得mg×2H-μmgcos α×=m
两滑块碰撞过程,由动量守恒定律得mv1=2mv共
当滑块再次滑上斜面时,由能量守恒定律得×2m=2mgH'+2μmgcos α×
其中H'=H
联立解得μ=0.3
(2)滑块第一次从斜面上滑下过程,由牛顿第二定律得mgsin α-μmgcos α=ma1
由运动学公式得v1=a1t1
滑块第一次滑上斜面的过程,由牛顿第二定律得2mgsin α+μ×2mgcos α=2ma2
由运动学公式得0-v共=-a2t2
联立解得t1∶t2=14∶3
(3)从滑块A由静止释放到滑块最终静止的整个过程,由能量守恒定律得mg×2H=m-2×m+W克f
由功能关系可知Q=W克f
联立解得Q=1.4mgH
9.(1)2 m/s (2)1.2 J
(3)s=
[解析] (1)物块进入光滑半圆轨道最高点并恰好做圆周运动,由牛顿第二定律得mg=m
`解得vB=2 m/s
(2)设物块到达A点时的速度为vA,物块被弹簧弹出过程中,物块和弹簧组成的系统机械能守恒,有Ep=m
由于vB>v0=1 m/s,可知物块在传送带上一直做匀减速运动,则物块在传送带上滑行过程,由动能定理可得-μ1mgL=m-m
联立解得Ep=1.2 J
(3)滑块从B到C过程中,由机械能守恒定律有m+mg·2R=m
解得vC=2 m/s
当μ2mg≤μ3(m+M)g,即μ3≥0.025时,长木块静止不动,要使小物块恰好不会从长木板上掉下,则物块在长木板上滑行过程,由动能定理得μ2mgs=m
解得s=4 m
当μ3<0.025时,长木板在小物块带动下做匀加速运动,小物块做匀减速运动,对物块有μ2mg=ma1
解得a1=2.5 m/s2
对长木板有μ2mg-μ3(m+M)g=Ma2
共速时有vC-a1t=a2t
木板的长度为s=t-t=
联立可得s= m(0<μ3<0.025)
综上所述,要使小物块恰好不会从长木板上掉下,木板长度s与木板和地面之间的动摩擦因数μ3的关系为
s=
微专题1 传送带模型综合问题 理-专项训练
1.(不定项)[2022·广东卷] 如图所示,载有防疫物资的无人驾驶小车,在水平MN段以恒定功率200 W、速度5 m/s匀速行驶,在斜坡PQ段以恒定功率570 W、速度2 m/s匀速行驶,已知小车总质量为50 kg,MN=PQ=20 m,PQ段的倾角为30°,重力加速度g取10 m/s2,不计空气阻力.下列说法正确的有 ( )
A.从M到N,小车牵引力大小为40 N
B.从M到N,小车克服摩擦力做功800 J
C.从P到Q,小车重力势能增加1×104 J
D.从P到Q,小车克服摩擦力做功700 J
2.如图所示为低空跳伞极限运动表演,运动员从离地350 m高的桥面一跃而下,实现了自然奇观与极限运动的完美结合.假设质量为m的跳伞运动员由静止开始下落,在打开伞之前受恒定阻力作用,下落的加速度为g(g为重力加速度),则在运动员下落h高度的过程中,下列说法正确的是 ( )
A.运动员重力做功为mgh
B.运动员克服阻力做功为mgh
C.运动员的动能增加了mgh
D.运动员的机械能减少了mgh
3.如图所示,轻弹簧上端固定,下端拴着一带正电的小球Q,Q在A处时弹簧处于原长状态,Q可在C处静止.当将另一带正电的小球q固定在C正下方某处时,Q可在B处静止.在有小球q的情况下,将Q从A处由静止释放,则Q从A运动到C处的过程中( )
A.Q运动到C处时速率最大
B.Q、q两球组成的系统机械能不断增大
C.Q的机械能不断增大
D.Q的加速度先减小后增大
4.(不定项)如图所示,一小物块由静止开始沿倾角为53°的斜面向下滑动,最后停在水平地面上.斜面和地面平滑连接,且物块与斜面间、物块与地面间的动摩擦因数均为,取地面为零势能面,已知sin 53°=0.8,cos 53°=0.6.该过程中,物块的机械能E、重力势能Ep、动能Ek、摩擦产生的热量Q与水平位移x的关系图像可能正确的是 ( )
A
B
C
D
5.电动车配有把机械能转化为电能的“能量回收”装置.某次测试中电动车沿倾角为15°的斜坡向下运动,初动能为1.0×105 J.第一次让车无动力自由滑行,其动能Ek与位移x的关系如图中直线①所示;第二次让车无动力并开启“能量回收”装置滑行,其动能Ek与位移x的关系如图中曲线②所示.假设机械能回收效率为90%,重力加速度g取10 m/s2.下列说法正确的是( )
A.图中①对应过程汽车所受合力越来越大
B.可求出图中②对应过程下滑200 m回收的电能
C.图中②对应过程下滑100 m后不再回收能量
D.由题中及图像信息可求出电动车的质量
6.(不定项)如图所示,倾斜成45°角的固定直杆上套有一质量为m的小球(可视为质点),小球可沿杆滑动,轻质弹性绳一端固定于O点,另一端连在小球上.将小球从弹性绳处于水平的位置M(此时弹性绳的长度为L)由静止释放,当小球运动到弹性绳与杆垂直的位置P时,弹性绳长度刚好为原长,小球沿杆下滑到弹性绳处于竖直的位置N时速度减为零.若弹性绳始终在弹性限度内且弹性绳的弹力与其形变量成正比,重力加速度大小为g,则下列说法正确的是 ( )
A.小球在P点时的加速度大小为g
B.从M到P的过程中,小球克服摩擦力做的功为mgL
C.小球在P点的动能等于从M到P的过程中弹性绳减小的弹性势能
D.小球从M到P的过程中损失的机械能小于从P到N的过程中损失的机械能
7.[2024·衢州模拟] 如图所示,两根粗糙的金属导轨平行放置在倾角为θ的斜面上,导轨下端接有电阻R,导轨电阻不计.斜面处在竖直向上的匀强磁场中,质量为m的金属棒ab垂直放置在导轨上且始终与导轨接触良好,金属棒电阻不计,重力加速度为g.若金属棒沿导轨减速下滑,在下滑h高度的过程中,它的速度由v0减小到v,则下列说法正确的是 ( )
A.作用在金属棒上的合力做的功为m-mv2
B.金属棒机械能的减少量为mgh+m-mv2
C.金属棒克服安培力做的功大于电阻R上产生的焦耳热
D.金属棒重力势能的减少量等于系统产生的电能
8.如图所示,左侧光滑曲面轨道与右侧倾角α=37°的斜面在底部平滑连接且均固定在光滑水平地面上,质量为m的小滑块A从斜面上离斜面底边高为2H处由静止释放,经过斜面与水平地面交接处时无机械能损失,在水平地面上与一质量为m的静止小滑块B发生正碰并结合为一个整体(A、B完全相同),一起滑上左侧曲面轨道,再从曲面轨道滑回斜面,滑块第一次沿斜面上滑的最大高度为H,多次往复运动.不计空气阻力,重力加速度为g,sin 37°=0.6,cos 37°=0.8.求:
(1)滑块与斜面间的动摩擦因数μ;
(2)滑块第一次滑下斜面的时间t1与第一次滑上斜面的时间t2之比;
(3)滑块最终静止,整个系统由于摩擦产生的热量Q.
9.[2024·温岭中学模拟] 如图所示,水平轨道左端与长L=1.25 m的水平传送带相接,传送带逆时针匀速运动的速度v0=1 m/s.轻弹簧右端固定在光滑水平轨道上,弹簧处于自然状态.现用质量m=0.1 kg的小物块(视为质点)将弹簧压缩后由静止释放,到达水平传送带左端B点后,立即沿切线进入竖直固定的光滑半圆轨道最高点并恰好做圆周运动,经圆周最低点C后滑上质量为M=0.9 kg的长木板上,竖直半圆轨道的半径R=0.4 m,物块与传送带间的动摩擦因数μ1=0.8,物块与木板间的动摩擦因数μ2=0.25.g取10 m/s2.
(1)求物块到达B点时的速度vB的大小;
(2)求弹簧被压缩时的弹性势能Ep;
(3)要使小物块恰好不会从长木板上掉下,求木板长度s与木板和地面之间的动摩擦因数μ3的关系(设最大静摩擦力等于滑动摩擦力).
参考答案与详细解析
1.ABD [解析] 匀速时F牵=Ff,在MN段F牵==40 N,故A正确;W克f=Ff=800 J,B正确;从P到Q,ΔEp=mgΔh,ΔEp=5×103 J,故C错误;从P到Q,F牵'==285 N,F牵'=Ff'+mgsin θ,解得Ff'=35 N,W克f'=Ff'=700 J,D正确.
2.C [解析] 运动员下落h高度,则重力做功为WG=mgh,选项A错误;根据牛顿第二定律得mg-Ff=ma,其中a=g,解得Ff=mg,则运动员克服阻力做功为W克f=Ffh=mgh,选项B错误;运动员的动能增加量等于合外力做的功,则ΔEk=mah=mgh,选项C正确;运动员的机械能减少量等于克服阻力做的功,即ΔE=W克f=mgh,选项D错误.
3.D [解析] 当小球q固定在C正下方某处时,Q在B处时所受的合力为零,在此处时速率最大,故A错误;Q的机械能E等于Q的动能与重力势能之和,由功能关系有ΔE=W弹+W电,Q从A处运动到C处的过程中,由于弹簧从原长一直在伸长,故弹簧的弹力一直做负功,即W弹<0,且库仑力也一直做负功,即W电<0,则ΔE<0,即Q的机械能不断减小,故C错误;因小球q固定不动,则其机械能不变,因Q的机械能不断变小,故Q、q两球组成的系统机械能不断减小,故B错误;Q在B处时加速度为零,则Q从A处运动到B的过程中,加速度一直减小到零,而Q从B处运动到C处的过程中,加速度反向增大,故D正确.
4.BD [解析] 设O点到斜面底端的距离为x0,物块释放点的高度为h,物块从释放到停止运动的过程中,当水平位移x≤x0时,克服摩擦力做功W克f=μmgcos 53°·=μmgx,当x>x0时,克服摩擦力做功W克f=μmgcos 53°·+μmg·(x-x0)=μmgx,所以全程都有W克f=μmgx=mgx,根据功能关系可知摩擦产生的热量Q=W克f=μmgx,而物块在该过程中机械能的减少量始终等于克服摩擦力所做的功,则物块的机械能E=mgh-mgx,所以E-x图像是纵轴截距为mgh、斜率为-mg的倾斜直线,而其Q-x图像是过原点、斜率为mg的倾斜直线,故A错误,D正确;物块的重力势能Ep=mgh-mgtan 53°·x=mgh-mgx,所以Ep-x图像是纵轴截距为mgh、斜率为-mg的倾斜直线,且当x>x0时,重力势能始终为0,故B正确;物块从最高点下滑至斜面最低点的过程中,物块的动能Ek1=mgxtan 53°-μmgcos 53°·=mgx(x≤x0),当物块下滑至斜面底端时,其动能Ek1=mgx0,此后在水平面上克服摩擦力做功,物块的动能Ek2=mgx0-μmg(x-x0)=mgx0-mgx(x0≤x≤2x0),所以动能达到最大值前,Ek-x图像是过原点的倾斜直线,斜率为mg,动能达到最大后,Ek-x图像仍是倾斜直线,斜率为-mg,图像具有对称性,故C错误.
5.B [解析] 由动能定理得F合x=ΔEk,故Ek-x图像的斜率表示合外力,由图像可知,图中①对应过程汽车所受合力不变,F合= N=500 N,故A错误;由图中①可知,汽车自由下滑200 m过程,有WG+Wf=×103 J,由图中②可知,开启能量回收模式下滑200 m过程,有WG+Wf+WF=×103 J,则回收的电能为E=-WF×90%=1.224×105 J,故B正确;图中②对应过程下滑100 m后动能不变,但是重力势能减少,机械能减少,所以还是继续回收能量,故C错误;由图中①可知,F合=mgsin 15°-μmgcos 15°=500 N,由于不知道车与斜坡间的动摩擦因数,故无法由题中及图像信息求出电动车的质量,故D错误.
6.BCD [解析] 根据几何关系可知OM与ON长度相等,则小球在M处和在N处时弹性绳的弹性势能相等,小球从M到N的过程中,由动能定理有mgL-W克f=0,说明小球运动过程中受到摩擦力的作用,小球在P点时,由牛顿第二定律可知,其加速度a=gsin 45°-
8.(1)0.3 (2)14∶3 (3)1.4 mgH
[解析] (1)当滑块A由斜面滑到水平面时,由能量守恒定律得mg×2H-μmgcos α×=m
两滑块碰撞过程,由动量守恒定律得mv1=2mv共
当滑块再次滑上斜面时,由能量守恒定律得×2m=2mgH'+2μmgcos α×
其中H'=H
联立解得μ=0.3
(2)滑块第一次从斜面上滑下过程,由牛顿第二定律得mgsin α-μmgcos α=ma1
由运动学公式得v1=a1t1
滑块第一次滑上斜面的过程,由牛顿第二定律得2mgsin α+μ×2mgcos α=2ma2
由运动学公式得0-v共=-a2t2
联立解得t1∶t2=14∶3
(3)从滑块A由静止释放到滑块最终静止的整个过程,由能量守恒定律得mg×2H=m-2×m+W克f
由功能关系可知Q=W克f
联立解得Q=1.4mgH
9.(1)2 m/s (2)1.2 J
(3)s=
[解析] (1)物块进入光滑半圆轨道最高点并恰好做圆周运动,由牛顿第二定律得mg=m
`解得vB=2 m/s
(2)设物块到达A点时的速度为vA,物块被弹簧弹出过程中,物块和弹簧组成的系统机械能守恒,有Ep=m
由于vB>v0=1 m/s,可知物块在传送带上一直做匀减速运动,则物块在传送带上滑行过程,由动能定理可得-μ1mgL=m-m
联立解得Ep=1.2 J
(3)滑块从B到C过程中,由机械能守恒定律有m+mg·2R=m
解得vC=2 m/s
当μ2mg≤μ3(m+M)g,即μ3≥0.025时,长木块静止不动,要使小物块恰好不会从长木板上掉下,则物块在长木板上滑行过程,由动能定理得μ2mgs=m
解得s=4 m
当μ3<0.025时,长木板在小物块带动下做匀加速运动,小物块做匀减速运动,对物块有μ2mg=ma1
解得a1=2.5 m/s2
对长木板有μ2mg-μ3(m+M)g=Ma2
共速时有vC-a1t=a2t
木板的长度为s=t-t=
联立可得s= m(0<μ3<0.025)
综上所述,要使小物块恰好不会从长木板上掉下,木板长度s与木板和地面之间的动摩擦因数μ3的关系为
s=
同课章节目录
