2025届高考物理二轮复习:微专题3 力学三大观点的综合运用-专项训练 (含解析)
文档属性
| 名称 | 2025届高考物理二轮复习:微专题3 力学三大观点的综合运用-专项训练 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 107.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-05 12:53:45 | ||
图片预览


文档简介
2025届高考物理二轮复习
微专题3 力学三大观点的综合运用-专项训练
1.[2024·温州中学模拟] 如图所示,光滑水平面MN的左端有一弹性挡板P(碰撞时无能量损失),右端N与处于同一高度的水平传送带之间的距离可忽略,传送带水平部分NQ的长度L=4 m,传送带逆时针匀速转动,其速度v=2 m/s.MN上放置着两个可视为质点的质量分别为mA=4 kg、mB=1 kg的小物块A、B,开始时A、B都静止,A、B间压缩一锁定的轻质弹簧,其弹性势能Ep=10 J.现解除锁定,弹簧弹开A、B后迅速移走弹簧,g取10 m/s2.
(1)求物块A、B被弹开时各自的速度大小;
(2)已知两物块将在水平面MN上发生碰撞,则小物块B与传送带间的动摩擦因数至少为多大
(3)若物块A、B与传送带间的动摩擦因数都等于第(2)问中的临界值,且两物块在水平面MN上碰撞后结合成整体,求在此后两物块整体第一次滑上传送带到第一次减速至零的过程中,两物块整体与传送带间因摩擦产生的热量.
2.[2024·宁波模拟] 如图所示为固定于竖直平面内的实验装置,该装置由A、B两端距离为L=4 m、速度可调的水平传送带及圆心分别在O1和O2、圆心角均为θ=120°、半径均为R=0.4 m的光滑圆弧轨道BCD与光滑细圆管EFG组成,其中B、G两点分别为两轨道的最高点和最低点,B点在传送带右端转轴的正上方.在细圆管EFG的右侧足够长的光滑水平地面上紧挨着一块与管口下端等高、足够长、质量M=0.5 kg的木板(与轨道不粘连).现将一块质量m=0.3 kg的物块(可视为质点)轻轻放在传送带的最左端A点,物块在传送带上自左向右运动,在B处的开口和E、D处的开口正好可容物块通过.已知物块与传送带之间的动摩擦因数μ1=0.2,物块与木板之间的动摩擦因数μ2=0.5,g取10 m/s2.
(1)若物块进入圆弧轨道BCD后恰好不脱轨,求传送带的速度大小;
(2)若传送带速度为5 m/s,求物块经过圆弧轨道BCD最低点D时,轨道对物块的弹力大小;
(3)若传送带最大速度为6 m/s,在不脱轨的情况下,求物块在木板上运动过程中产生的热量Q与传送带速度v之间的关系.
3.[2024·效实中学模拟] 某游戏装置如图所示,左侧固定一张长s=1.75 m的桌子,水平桌面的边缘A、B处有两个小物块甲、乙,质量分别为m1=0.08 kg,m2=0.02 kg,两物块与桌面之间的动摩擦因数均为μ=0.2;右侧有一根不可伸长的细线,长度为L=1.5 m,能够承受的最大拉力Fmax=16 N,细线上端固定在O点,下端系有一个侧面开口的轻盒(质量不计),初始时刻盒子锁定在C点且细线伸直,OC与竖直方向的夹角θ=37°,O点正下方距离为h=0.5 m处有一细长的钉子,用于阻挡细线.某次游戏时,敲击物块甲,使其获得v0=4 m/s的初速度,一段时间后与物块乙发生碰撞,碰撞时间极短且碰后粘在一起,形成组合体从边缘B飞出,当组合体沿垂直于OC方向飞入盒子时,盒子立即解锁,之后组合体与盒子一起运动不再分离.若组合体碰撞盒子前后速度不变,空气阻力不计,物块与轻盒大小可忽略,sin 37°=0.6,cos 37°=0.8,g取10 m/s2.
(1)求物块甲即将碰到乙时的速度大小v1;
(2)求组合体到达C点时的速度大小vC;
(3)求细线被钉子挡住后的瞬间对盒子的拉力大小FT;
(4)若h的大小可调,要求细线被钉子挡住后始终伸直且不断裂,求h的可调范围.
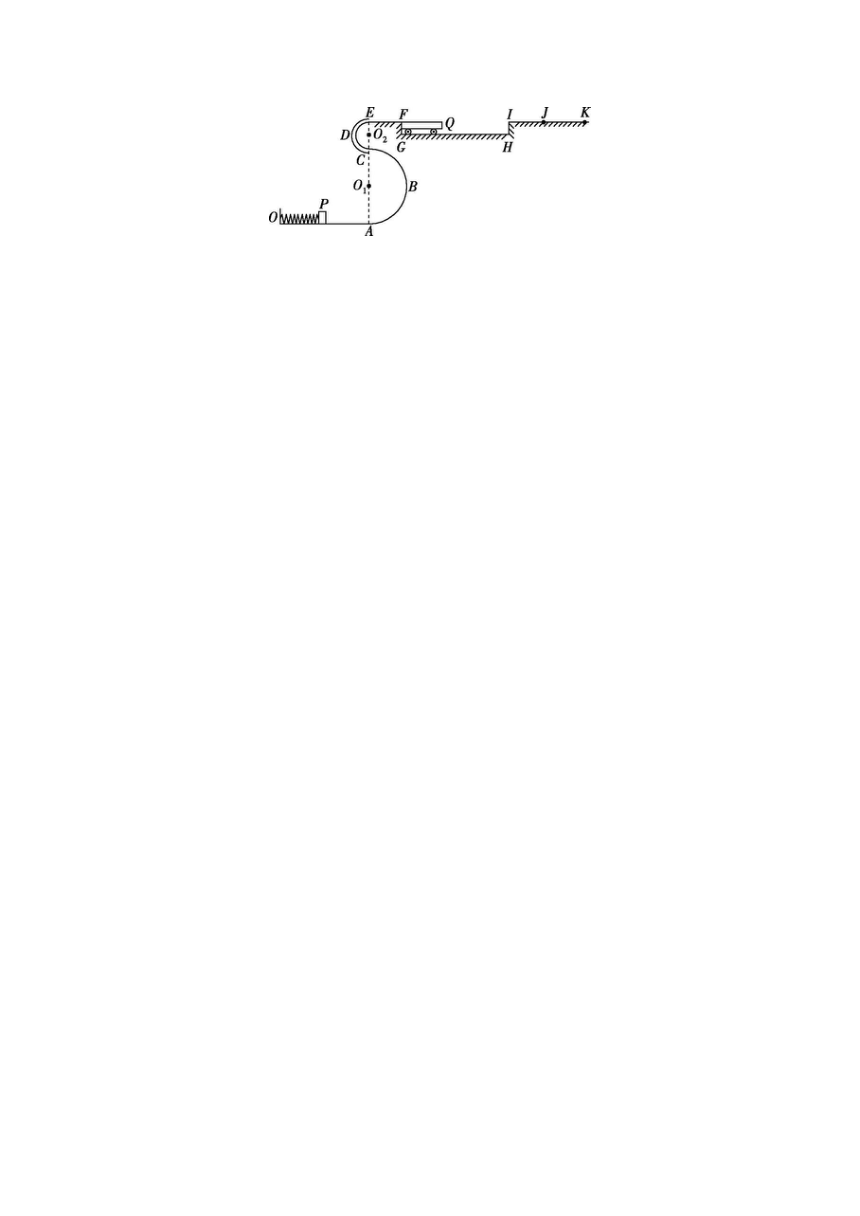
4.[2024·湖州模拟] 物理老师自制了一套游戏装置供同学们一起娱乐和研究,游戏装置可以简化为如图所示的模型.该模型由同一竖直平面内的水平轨道OA、半径为R1=0.6 m的半圆单层轨道ABC、半径为R2=0.1 m的半圆圆管轨道CDE、平台EF和IK、凹槽FGHI组成,且各段各处平滑连接.凹槽里停放着一辆质量为m=0.1 kg的无动力摆渡车Q并紧靠在竖直侧壁FG处,摆渡车长度L1=1 m且上表面与平台EF、IK平齐.水平面OA的左端通过挡板固定一个弹簧,弹簧右端可以通过压缩弹簧发射能看成质点的不同滑块P,弹簧的弹性势能最大能达到Epm=5.8 J.现三位同学小张、小杨、小振分别选择了质量为m1=0.1 kg、m2=0.2 kg、m3=0.4 kg的同种材质滑块P参与游戏,游戏成功的标准是通过弹簧发射出去的滑块能停在平台的目标区JK段.已知凹槽GH段足够长,摆渡车与侧壁IH相撞时会立即停止不动,滑块与摆渡车上表面和平台IK段间的动摩擦因数都是μ=0.5,其余各处摩擦都不计,IJ段长度L2=0.4 m,JK段长度L3=0.7 m,g取10 m/s2.
(1)已知小振同学的滑块以最大弹性势能弹出时不能进入圆管轨道,求小振同学的滑块经过与圆心O1等高的B处时对轨道的最大压力;
(2)如果小张同学以Ep1=2 J的弹性势能将滑块弹出,请根据计算后判断滑块最终停在何处
(3)如果小杨将滑块弹出后滑块最终能成功地停在目标区JK段,则他发射时的弹性势能Ep应满足什么要求
参考答案与详细解析
1.(1)1 m/s 4 m/s (2)0.2 (3)4.4 J或15.6 J
[解析] (1)A、B物块被弹簧弹开的过程中,由动量守恒定律得mAvA-mBvB=0
由能量守恒定律得Ep=mA+mB
联立解得vA=1 m/s,vB=4 m/s
(2)要使两物块能在水平面MN上发生碰撞,小物块B不能在传送带的Q端掉下,则小物块B在传送带上最多减速运动到Q端时速度减为零.
设减速过程加速度大小至少为a,动摩擦因数至少为μ,由牛顿第二定律得μmBg=mBa
由运动学公式得0-=-2aL
联立解得 μ=0.2
(3)因为物块B第一次冲上传送带的速度vB=4 m/s大于传送带的速度v=2 m/s,所以物块B在传送带上返回水平面MN上过程先加速运动后匀速运动,到达水平面MN上时的速度等于传送带速度,即vB'=v=2 m/s.
①若两物块A、B在水平面MN上相向碰撞结合成整体,设碰后共同速度为v1,根据动量守恒定律得mAvA-mBvB'=(mA+mB)v1
解得v1=0.4 m/s,方向向右
两物块整体第一次滑上传送带到第一次减速至零的过程,所用时间为t1=
两物块整体与传送带的相对位移为Δx1=vt1+v1t1
两物块与传送带间因摩擦产生的热量为Q1=μ(mA+mB)g·Δx1
联立解得Q1=4.4 J
②若两物块A、B在水平面MN上同向碰撞结合成整体,设碰后共同速度为v2,根据动量守恒定律得
mAvA+mBvB'=(mA+mB)v2
解得v2=1.2 m/s,方向向左
两物块整体与弹性挡板P碰撞无能量损失,碰后速度大小仍为v2=1.2 m/s,方向向右
两物块整体第一次滑上传送带到第一次减速至零的过程,所用时间为t2=
两物块整体与传送带的相对位移为Δx2=vt2+v2t2
两物块与传送带间因摩擦产生的热量为Q2=μ(mA+mB)g·Δx2
联立解得Q2=15.6 J
综上可知,两物块整体与传送带间因摩擦产生的热量是4.4 J或15.6 J.
2.(1)2 m/s (2)22.5 N
(3)Q=
[解析] (1)若物块进入圆弧轨道BCD后恰好不脱轨,则物块在B点时,由牛顿第二定律得mg=m
解得vB0=2 m/s
物块在传送带上运动过程,根据牛顿第二定律得μ1mg=ma
若传送带速度较大,物块在传送带上能一直加速运动到B端,则由运动学公式得=2aL
解得v1=4 m/s
由于v1>vB0=2 m/s,所以物块的运动不是一直加速运动,而是先加速到与传送带共速再与传送带一起匀速运动,传送带的速度为2 m/s
(2)传送带速度为5 m/s时,由于v1<5 m/s,所以物块在传送带上匀加速运动到B端.物块在圆弧轨道BCD上运动过程,根据动能定理得mg[R+Rsin(θ-90°)]=m-m
物块经过D点时,由牛顿第二定律得FND-mgsin (θ-90°)=m
联立解得FND=22.5 N
(3)在不脱轨的情况下,物块从B点运动到G点的过程,根据动能定理得mg[2R+2Rsin(θ-90°)]=m-m
物块在木板上运动过程中,物块和木板组成的系统动量守恒,有mvG=v
由能量守恒定律得Q=m-(m+M)v2
联立可得Q=(J)
当传送带的速度v的取值范围为2 m/s≤v<4 m/s时,滑块到达B时速度为vB=v,产生的热量为Q= (J)
当传送带的速度v的取值范围为4 m/s≤v≤6 m/s时,滑块到达B时速度为vB=4 m/s,产生的热量为Q= J
综上可知,
Q=
3.(1)3 m/s (2)3 m/s (3)2.5 N (4)0[解析] (1)物块甲与乙碰撞前向右做匀减速直线运动,根据动能定理有-μm1gs=m1-m1
解得v1=3 m/s
(2)物块甲与乙发生完全非弹性碰撞,根据动量守恒定律有m1v1=v2
碰撞后,组合体做平抛运动,在C点时,对速度分解,有vCcos θ=v2
联立解得vC=3 m/s
(3)组合体从C点运动到钉子正下方时,根据动能定理有g(L-Lcos θ)=-(m1+m2)
解得v3= m/s
细线被钉子挡住后的瞬间,对盒子(含物块组合体),由牛顿第二定律有FT-g=(m1+m2)
解得FT=2.5 N
(4)当盒子刚好能摆到钉子等高处时,对盒子整体,由动能定理得-(m1+m2)g(L-h1)=0-(m1+m2)
解得h1=0.75 m
当盒子能绕钉子做完整的圆周运动且刚好通过最高点时,对盒子整体,由动能定理得
-g·2=(m1+m2)v2-v32
在最高点时,由牛顿第二定律得
g=
联立解得h2=1.2 m
在该条件下同时需满足在最低点绳子不断裂,由牛顿第二定律得Fmax-g=
解得h3=1.4 m
综上可知,h的可调范围为04.(1) N (2)在I点左侧距离为0.1 m处 (3)4.6 J≤Ep≤5.5 J
[解析] (1)当小振同学的滑块以最大弹性势能弹出时,滑块经过与圆心O1等高的B处时对轨道的压力最大.
从弹出到B处,根据动能定理有Epm-m3gR1=m3
经过B处时,由牛顿第二定律得FN=m3
由牛顿第三定律可知,滑块经过与圆心O1等高的B处时对轨道的最大压力FN'=FN
联立解得FN'= N
(2)当小张同学的滑块刚好经过C时,由牛顿第二定律得m1g=m1
解得vC1= m/s
假设滑块在C点不脱离轨道,则由能量守恒定律得Ep1=2m1gR1+m1
解得vC=4 m/s
由于vC>vC1,所以假设成立.
假设滑块能运动到平台上,则由能量守恒定律得Ep1=2m1g+m1
解得v1=2 m/s
所以假设成立,且滑块到达摆渡车左端时速度为2 m/s
由于凹槽足够长,故摆渡车与侧壁IH相撞前滑块与摆渡车已经共速,设共速时滑块与摆渡车的相对位移为s,则根据动量守恒定律有m1v1=v共1
根据功能关系有μm1gs=m1-
联立解得s=0.6 m
之后滑块与摆渡车一起匀速运动,摆渡车与侧壁IH相撞后会立即停止不动,滑块继续向前滑行,滑块速度减小到零的过程,由动能定理得-μm1gs'=0-m1
联立解得s'=0.3 m
由于s+s'(3)当小杨的滑块刚好经过C时,由牛顿第二定律得m2g=m2
所以他发射时的弹性势能应满足Ep≥2m2gR1+m2
滑块从弹出至运动到平台上,根据动能定理有Ep-2m2g=m2v2
由于凹槽足够长,所以滑块与摆渡车能达到共速,由动量守恒定律得m2v=v共2
对整个过程,由能量守恒定律得Ep=2m2g+m+μm2gs1
要使得滑块停在目标区,应满足L1+L2≤s1≤L1+L2+L3
联立解得4.6 J≤Ep≤5.5 J,且0≤Ep≤5.8 J
故当小杨同学游戏能成功时,他发射时的弹性势能Ep的取值范围为4.6 J≤Ep≤5.5 J
微专题3 力学三大观点的综合运用-专项训练
1.[2024·温州中学模拟] 如图所示,光滑水平面MN的左端有一弹性挡板P(碰撞时无能量损失),右端N与处于同一高度的水平传送带之间的距离可忽略,传送带水平部分NQ的长度L=4 m,传送带逆时针匀速转动,其速度v=2 m/s.MN上放置着两个可视为质点的质量分别为mA=4 kg、mB=1 kg的小物块A、B,开始时A、B都静止,A、B间压缩一锁定的轻质弹簧,其弹性势能Ep=10 J.现解除锁定,弹簧弹开A、B后迅速移走弹簧,g取10 m/s2.
(1)求物块A、B被弹开时各自的速度大小;
(2)已知两物块将在水平面MN上发生碰撞,则小物块B与传送带间的动摩擦因数至少为多大
(3)若物块A、B与传送带间的动摩擦因数都等于第(2)问中的临界值,且两物块在水平面MN上碰撞后结合成整体,求在此后两物块整体第一次滑上传送带到第一次减速至零的过程中,两物块整体与传送带间因摩擦产生的热量.
2.[2024·宁波模拟] 如图所示为固定于竖直平面内的实验装置,该装置由A、B两端距离为L=4 m、速度可调的水平传送带及圆心分别在O1和O2、圆心角均为θ=120°、半径均为R=0.4 m的光滑圆弧轨道BCD与光滑细圆管EFG组成,其中B、G两点分别为两轨道的最高点和最低点,B点在传送带右端转轴的正上方.在细圆管EFG的右侧足够长的光滑水平地面上紧挨着一块与管口下端等高、足够长、质量M=0.5 kg的木板(与轨道不粘连).现将一块质量m=0.3 kg的物块(可视为质点)轻轻放在传送带的最左端A点,物块在传送带上自左向右运动,在B处的开口和E、D处的开口正好可容物块通过.已知物块与传送带之间的动摩擦因数μ1=0.2,物块与木板之间的动摩擦因数μ2=0.5,g取10 m/s2.
(1)若物块进入圆弧轨道BCD后恰好不脱轨,求传送带的速度大小;
(2)若传送带速度为5 m/s,求物块经过圆弧轨道BCD最低点D时,轨道对物块的弹力大小;
(3)若传送带最大速度为6 m/s,在不脱轨的情况下,求物块在木板上运动过程中产生的热量Q与传送带速度v之间的关系.
3.[2024·效实中学模拟] 某游戏装置如图所示,左侧固定一张长s=1.75 m的桌子,水平桌面的边缘A、B处有两个小物块甲、乙,质量分别为m1=0.08 kg,m2=0.02 kg,两物块与桌面之间的动摩擦因数均为μ=0.2;右侧有一根不可伸长的细线,长度为L=1.5 m,能够承受的最大拉力Fmax=16 N,细线上端固定在O点,下端系有一个侧面开口的轻盒(质量不计),初始时刻盒子锁定在C点且细线伸直,OC与竖直方向的夹角θ=37°,O点正下方距离为h=0.5 m处有一细长的钉子,用于阻挡细线.某次游戏时,敲击物块甲,使其获得v0=4 m/s的初速度,一段时间后与物块乙发生碰撞,碰撞时间极短且碰后粘在一起,形成组合体从边缘B飞出,当组合体沿垂直于OC方向飞入盒子时,盒子立即解锁,之后组合体与盒子一起运动不再分离.若组合体碰撞盒子前后速度不变,空气阻力不计,物块与轻盒大小可忽略,sin 37°=0.6,cos 37°=0.8,g取10 m/s2.
(1)求物块甲即将碰到乙时的速度大小v1;
(2)求组合体到达C点时的速度大小vC;
(3)求细线被钉子挡住后的瞬间对盒子的拉力大小FT;
(4)若h的大小可调,要求细线被钉子挡住后始终伸直且不断裂,求h的可调范围.
4.[2024·湖州模拟] 物理老师自制了一套游戏装置供同学们一起娱乐和研究,游戏装置可以简化为如图所示的模型.该模型由同一竖直平面内的水平轨道OA、半径为R1=0.6 m的半圆单层轨道ABC、半径为R2=0.1 m的半圆圆管轨道CDE、平台EF和IK、凹槽FGHI组成,且各段各处平滑连接.凹槽里停放着一辆质量为m=0.1 kg的无动力摆渡车Q并紧靠在竖直侧壁FG处,摆渡车长度L1=1 m且上表面与平台EF、IK平齐.水平面OA的左端通过挡板固定一个弹簧,弹簧右端可以通过压缩弹簧发射能看成质点的不同滑块P,弹簧的弹性势能最大能达到Epm=5.8 J.现三位同学小张、小杨、小振分别选择了质量为m1=0.1 kg、m2=0.2 kg、m3=0.4 kg的同种材质滑块P参与游戏,游戏成功的标准是通过弹簧发射出去的滑块能停在平台的目标区JK段.已知凹槽GH段足够长,摆渡车与侧壁IH相撞时会立即停止不动,滑块与摆渡车上表面和平台IK段间的动摩擦因数都是μ=0.5,其余各处摩擦都不计,IJ段长度L2=0.4 m,JK段长度L3=0.7 m,g取10 m/s2.
(1)已知小振同学的滑块以最大弹性势能弹出时不能进入圆管轨道,求小振同学的滑块经过与圆心O1等高的B处时对轨道的最大压力;
(2)如果小张同学以Ep1=2 J的弹性势能将滑块弹出,请根据计算后判断滑块最终停在何处
(3)如果小杨将滑块弹出后滑块最终能成功地停在目标区JK段,则他发射时的弹性势能Ep应满足什么要求
参考答案与详细解析
1.(1)1 m/s 4 m/s (2)0.2 (3)4.4 J或15.6 J
[解析] (1)A、B物块被弹簧弹开的过程中,由动量守恒定律得mAvA-mBvB=0
由能量守恒定律得Ep=mA+mB
联立解得vA=1 m/s,vB=4 m/s
(2)要使两物块能在水平面MN上发生碰撞,小物块B不能在传送带的Q端掉下,则小物块B在传送带上最多减速运动到Q端时速度减为零.
设减速过程加速度大小至少为a,动摩擦因数至少为μ,由牛顿第二定律得μmBg=mBa
由运动学公式得0-=-2aL
联立解得 μ=0.2
(3)因为物块B第一次冲上传送带的速度vB=4 m/s大于传送带的速度v=2 m/s,所以物块B在传送带上返回水平面MN上过程先加速运动后匀速运动,到达水平面MN上时的速度等于传送带速度,即vB'=v=2 m/s.
①若两物块A、B在水平面MN上相向碰撞结合成整体,设碰后共同速度为v1,根据动量守恒定律得mAvA-mBvB'=(mA+mB)v1
解得v1=0.4 m/s,方向向右
两物块整体第一次滑上传送带到第一次减速至零的过程,所用时间为t1=
两物块整体与传送带的相对位移为Δx1=vt1+v1t1
两物块与传送带间因摩擦产生的热量为Q1=μ(mA+mB)g·Δx1
联立解得Q1=4.4 J
②若两物块A、B在水平面MN上同向碰撞结合成整体,设碰后共同速度为v2,根据动量守恒定律得
mAvA+mBvB'=(mA+mB)v2
解得v2=1.2 m/s,方向向左
两物块整体与弹性挡板P碰撞无能量损失,碰后速度大小仍为v2=1.2 m/s,方向向右
两物块整体第一次滑上传送带到第一次减速至零的过程,所用时间为t2=
两物块整体与传送带的相对位移为Δx2=vt2+v2t2
两物块与传送带间因摩擦产生的热量为Q2=μ(mA+mB)g·Δx2
联立解得Q2=15.6 J
综上可知,两物块整体与传送带间因摩擦产生的热量是4.4 J或15.6 J.
2.(1)2 m/s (2)22.5 N
(3)Q=
[解析] (1)若物块进入圆弧轨道BCD后恰好不脱轨,则物块在B点时,由牛顿第二定律得mg=m
解得vB0=2 m/s
物块在传送带上运动过程,根据牛顿第二定律得μ1mg=ma
若传送带速度较大,物块在传送带上能一直加速运动到B端,则由运动学公式得=2aL
解得v1=4 m/s
由于v1>vB0=2 m/s,所以物块的运动不是一直加速运动,而是先加速到与传送带共速再与传送带一起匀速运动,传送带的速度为2 m/s
(2)传送带速度为5 m/s时,由于v1<5 m/s,所以物块在传送带上匀加速运动到B端.物块在圆弧轨道BCD上运动过程,根据动能定理得mg[R+Rsin(θ-90°)]=m-m
物块经过D点时,由牛顿第二定律得FND-mgsin (θ-90°)=m
联立解得FND=22.5 N
(3)在不脱轨的情况下,物块从B点运动到G点的过程,根据动能定理得mg[2R+2Rsin(θ-90°)]=m-m
物块在木板上运动过程中,物块和木板组成的系统动量守恒,有mvG=v
由能量守恒定律得Q=m-(m+M)v2
联立可得Q=(J)
当传送带的速度v的取值范围为2 m/s≤v<4 m/s时,滑块到达B时速度为vB=v,产生的热量为Q= (J)
当传送带的速度v的取值范围为4 m/s≤v≤6 m/s时,滑块到达B时速度为vB=4 m/s,产生的热量为Q= J
综上可知,
Q=
3.(1)3 m/s (2)3 m/s (3)2.5 N (4)0
解得v1=3 m/s
(2)物块甲与乙发生完全非弹性碰撞,根据动量守恒定律有m1v1=v2
碰撞后,组合体做平抛运动,在C点时,对速度分解,有vCcos θ=v2
联立解得vC=3 m/s
(3)组合体从C点运动到钉子正下方时,根据动能定理有g(L-Lcos θ)=-(m1+m2)
解得v3= m/s
细线被钉子挡住后的瞬间,对盒子(含物块组合体),由牛顿第二定律有FT-g=(m1+m2)
解得FT=2.5 N
(4)当盒子刚好能摆到钉子等高处时,对盒子整体,由动能定理得-(m1+m2)g(L-h1)=0-(m1+m2)
解得h1=0.75 m
当盒子能绕钉子做完整的圆周运动且刚好通过最高点时,对盒子整体,由动能定理得
-g·2=(m1+m2)v2-v32
在最高点时,由牛顿第二定律得
g=
联立解得h2=1.2 m
在该条件下同时需满足在最低点绳子不断裂,由牛顿第二定律得Fmax-g=
解得h3=1.4 m
综上可知,h的可调范围为0
[解析] (1)当小振同学的滑块以最大弹性势能弹出时,滑块经过与圆心O1等高的B处时对轨道的压力最大.
从弹出到B处,根据动能定理有Epm-m3gR1=m3
经过B处时,由牛顿第二定律得FN=m3
由牛顿第三定律可知,滑块经过与圆心O1等高的B处时对轨道的最大压力FN'=FN
联立解得FN'= N
(2)当小张同学的滑块刚好经过C时,由牛顿第二定律得m1g=m1
解得vC1= m/s
假设滑块在C点不脱离轨道,则由能量守恒定律得Ep1=2m1gR1+m1
解得vC=4 m/s
由于vC>vC1,所以假设成立.
假设滑块能运动到平台上,则由能量守恒定律得Ep1=2m1g+m1
解得v1=2 m/s
所以假设成立,且滑块到达摆渡车左端时速度为2 m/s
由于凹槽足够长,故摆渡车与侧壁IH相撞前滑块与摆渡车已经共速,设共速时滑块与摆渡车的相对位移为s,则根据动量守恒定律有m1v1=v共1
根据功能关系有μm1gs=m1-
联立解得s=0.6 m
之后滑块与摆渡车一起匀速运动,摆渡车与侧壁IH相撞后会立即停止不动,滑块继续向前滑行,滑块速度减小到零的过程,由动能定理得-μm1gs'=0-m1
联立解得s'=0.3 m
由于s+s'
所以他发射时的弹性势能应满足Ep≥2m2gR1+m2
滑块从弹出至运动到平台上,根据动能定理有Ep-2m2g=m2v2
由于凹槽足够长,所以滑块与摆渡车能达到共速,由动量守恒定律得m2v=v共2
对整个过程,由能量守恒定律得Ep=2m2g+m+μm2gs1
要使得滑块停在目标区,应满足L1+L2≤s1≤L1+L2+L3
联立解得4.6 J≤Ep≤5.5 J,且0≤Ep≤5.8 J
故当小杨同学游戏能成功时,他发射时的弹性势能Ep的取值范围为4.6 J≤Ep≤5.5 J
同课章节目录
