2025届高考物理二轮复习:微专题4 质谱仪、回旋加速器等组合场问题-专项训练 (含解析)
文档属性
| 名称 | 2025届高考物理二轮复习:微专题4 质谱仪、回旋加速器等组合场问题-专项训练 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 177.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-05 12:54:43 | ||
图片预览


文档简介
2025届高考物理二轮复习
微专题4 质谱仪、回旋加速器等组合场问题-专项训练
1.[2024·杭州模拟] 质谱仪是检测和分离同位素的仪器.如图所示,速度选择器中磁感应强度为B1,方向垂直于纸面向里,电场强度为E.分离器中磁感应强度为B2,方向垂直于纸面向外.离子室内充有大量氦的同位素离子,经加速电场加速后从速度选择器两极板间的中点O平行于极板进入,选择出的部分离子通过小孔O'进入分离器的磁场中,在底片上形成3个有一定宽度的分别对应He、He和He三种离子的感光区域,第一个感光区域的中心P到O'点的距离为d1.忽略离子的重力及相互间作用力,不计小孔O'的孔径.
(1)求沿直线运动通过速度选择器并打在感光区域中心P点的离子的速度大小v0及比荷;
(2)以速度为v=v0±Δv从O点射入的离子在速度选择器中的运动可视作速度为v0的匀速直线运动和速度为Δv的匀速圆周运动的合运动,要使感光板上出现3个有一定宽度的感光区域,求该速度选择器极板的最小长度L;
(3)在(2)的情况下,为能区分3种离子,求该速度选择器的极板间最大间距d.
2.[2024·湖州模拟] 质谱仪被广泛应用于同位素的研究.如图所示为某款质谱仪的原理结构图.初速度可以忽略的带电粒子由粒子源S飘出,经过M、N间电压为U的加速电场加速后,沿轴线OO'飞入右侧圆形匀强磁场区域(O'为磁场区域的圆心),经磁场偏转后粒子打在磁场下方的平板记录仪AC上.已知磁场区域半径为R,磁感应强度大小为B(方向与纸面垂直),记录仪AC长度为2R,与磁场区域的下边界相切于其中点D.整个装置处于真空中,不计粒子重力,不考虑粒子间的相互作用.
(1)求打在记录板上D点的粒子的比荷;
(2)若氕核(H)恰好打在记录板上D点时,求氚核(H)打在记录板上的位置;
(3)若匀强磁场区域的磁感应强度大小的波动范围为B±ΔB,为使氕核(H)与氚核(H)在记录板上的位置分开,求应满足的条件.
3.[2024·余姚模拟] 清华大学研究的新型SSMB-EUV光刻技术用于提供高强度、可调波长的极紫外光源.方案中的同步轨道如图所示,密度分布非常均匀的稳流电子束被导入同步轨道.同步轨道上存在垂直轨道平面的磁感应强度为B的匀强磁场,电子在磁场控制下沿着固定半径的轨道做匀速圆周运动,每转一周,穿越一次加速腔,从中获得能量,如图所示.同步加速器中磁感应强度随电子速度的增加而增加.已知圆形轨道半径为R,电子的质量为m,电荷量为-e,加速腔ab的长度为L,L R,当电子进入加速腔时,加速电压的大小始终为U,离开加速腔后,加速腔的电压变为0,加速电场的频率与电子的回旋频率保持同步.已知加速腔外无电场,腔内无磁场,不考虑重力、相对论效应以及粒子间相互作用.
(1)当电子在同步轨道中的动能为Ek时,求轨道处的磁感应强度B的大小.
(2)长度为d(d(3)注入初动能为Ek、长度为d的电子束,最多可以被加速腔加速几次
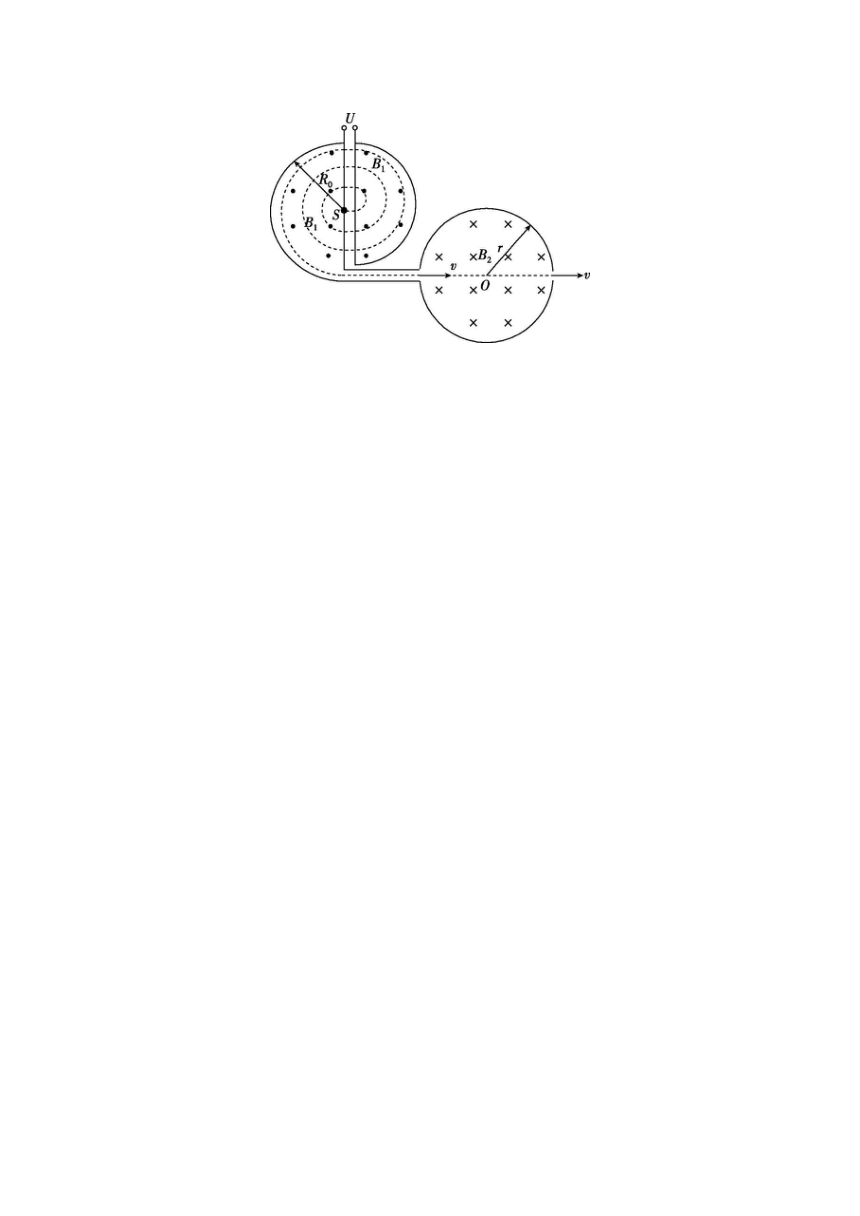
4.如图所示,有一回旋加速器,两D形盒加上垂直于纸面外、磁感应强度B1可调节的匀强磁场,左盒通过一水平管道与一个左右两侧都开有很小狭缝的圆筒相连,圆筒内有垂直于纸面向内的匀强磁场.现在左盒附近的点S放置一电子,再利用两盒间的狭缝加上一交变电压来给电子周期性加速,经过时间t电子便获得一定速率贴着管壁通过水平管道后进入圆筒,与下圆筒壁发生多次弹性碰撞又不作循环地从圆筒的右狭缝直接离开圆筒.已知圆筒的半径为r,磁感应强度恒为B2,D形盒的半径为R0,电子的比荷为,电子在两D形盒间的狭缝中运动的时间不计,加速电子时电压的大小可视为不变,电子重力不计.
(1)求与下圆筒壁碰撞n次的电子的速率;
(2)由(1)的速率确定D形盒中磁感应强度B1的表达式,并求n=2时B1的值;
(3)若电子在狭缝中加速次数与回旋半周的次数相同,根据n=2时B1的值及其他已知量求加速电压U的值.
参考答案与详细解析
1.(1) (2)
(3)d1
[解析] (1)离子在速度选择器中沿直线运动,则电场力与洛伦兹力平衡,有qv0B1=qE
解得v0=
由几何关系可知,打在感光区域中心P点的离子在分离器中做圆周运动的半径r1=
由洛伦兹力提供向心力,有qv0B2=m
联立解得=
(2)离子在加速电场中加速过程,根据动能定理得qU=m
离子在分离器中做匀速圆周运动,由洛伦兹力提供向心力,有
qv0B2=m
联立可得r=
三种离子的电荷量相同,则质量最小的He做圆周运动的轨迹半径最小,所以(1)中所解比荷对应He.He、He和He三种离子在速度选择器内的磁场中做圆周运动的周期分别为
T1==
T2==
T2==
要使感光板上出现3个有一定宽度的感光区域,三种离子应都能通过速度选择器,三种离子在速度选择器中都应运动整数个周期,则运动时间最小为t0=20T1
所以速度选择器极板的最小长度L=v0t0=.
(3)离子在速度选择器中做圆周运动这一分运动的最大半径为,对三种离子都有===
He在分离器中做匀速圆周运动的最大直径为
Dm1==d1+=d1+×=d1+×
同理,He在分离器中做匀速圆周运动的最小直径为Dm2==d1-×
He在分离器中做匀速圆周运动的最大直径为Dm2'=d1+×
He在分离器中做匀速圆周运动的最小直径为Dm3==d1-×
为能区分3种离子,应满足
Dm1Dm2'联立解得d因此该速度选择器的极板间最大间距为d1.
2.(1) (2)D点右侧距离为R处 (3)≤2-
[解析] (1)当粒子打在记录板上D点时,如图甲所示
根据几何关系可知,粒子在匀强磁场中做匀速圆周运动的半径r=R
粒子在加速电场中加速过程,根据动能定理得qU=mv2
粒子在磁场中做匀速圆周运动,根据洛伦兹力提供向心力可得qvB=m
联立解得=
(2)设H在磁场中做匀速圆周运动的半径为r1,在加速电场中加速过程,根据动能定理得q1U=m1
在磁场中做匀速圆周运动,根据洛伦兹力提供向心力得q1v1B=m1
联立解得r1=
同理,H在磁场中做匀速圆周运动的半径r2=
由于q2=q1,m2=3m1
所以=
H恰好打在记录板上D点,由几何关系可知r1=R
则r2=R
H在磁场中的运动轨迹如图乙所示
由几何关系可知tan =
解得θ=60°
则α=180°-θ=120°
H打在D点右侧与D点的距离为x=Rtan (α-90°)=R
(3)若H在磁感应强度为B-ΔB时与H在磁感应强度为B+ΔB时打在记录板上同一位置,则两粒子的轨迹恰好不重合,此时做匀速圆周运动的半径相等,有
=
解得ΔB=(2-)B
所以应满足的条件为≤2-
3.(1) (2)d (3)
[解析] (1)电子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,有evB=m
又知Ek=mv2
联立解得B=
(2)某次电子束被加速前长度d=v0Δt
其中m=Ek
加速一次过程,由动能定理有eU=m-Ek
电子束被加速一次后长度为d1=v1Δt
联立解得d1=d
(3)注入初动能为Ek、长度为d的电子束,可以被加速腔加速n次,由动能定理有neU=m-Ek
加速后的长度dn=vnΔt
应满足dn≤L
联立解得n≤
即最多可以被加速腔加速次数为
4.(1)tan (n=1,2,3,…)
(2)B1=tan (n=1,2,3,…) (3)
[解析] (1)电子在圆筒中既碰撞又做圆周运动的情形呈现周期性和对称性,作出两种情况为例,如图所示
电子做圆周运动的一个单元夹角θ=(n=1,2,3,…)
由几何关系可知,电子做圆周运动的半径R=rtan θ
由洛伦兹力提供向心力有evB2=m
联立解得电子与下圆筒壁碰撞n次的电子的速率为v=tan (n=1,2,3,…)
(2)电子在回旋加速器中运动刚离开时,由洛伦兹力提供向心力,有eB1v=m
解得B1=tan (n=1,2,3,…)
当n=2时,B1=
(3)电子在回旋加速器中做匀速圆周运动的周期T=
加速的次数为N=
加速N次过程中,由动能定理得N·eU=mv2
当n=2时,v=,B1=
联立解得加速电压为U=
微专题4 质谱仪、回旋加速器等组合场问题-专项训练
1.[2024·杭州模拟] 质谱仪是检测和分离同位素的仪器.如图所示,速度选择器中磁感应强度为B1,方向垂直于纸面向里,电场强度为E.分离器中磁感应强度为B2,方向垂直于纸面向外.离子室内充有大量氦的同位素离子,经加速电场加速后从速度选择器两极板间的中点O平行于极板进入,选择出的部分离子通过小孔O'进入分离器的磁场中,在底片上形成3个有一定宽度的分别对应He、He和He三种离子的感光区域,第一个感光区域的中心P到O'点的距离为d1.忽略离子的重力及相互间作用力,不计小孔O'的孔径.
(1)求沿直线运动通过速度选择器并打在感光区域中心P点的离子的速度大小v0及比荷;
(2)以速度为v=v0±Δv从O点射入的离子在速度选择器中的运动可视作速度为v0的匀速直线运动和速度为Δv的匀速圆周运动的合运动,要使感光板上出现3个有一定宽度的感光区域,求该速度选择器极板的最小长度L;
(3)在(2)的情况下,为能区分3种离子,求该速度选择器的极板间最大间距d.
2.[2024·湖州模拟] 质谱仪被广泛应用于同位素的研究.如图所示为某款质谱仪的原理结构图.初速度可以忽略的带电粒子由粒子源S飘出,经过M、N间电压为U的加速电场加速后,沿轴线OO'飞入右侧圆形匀强磁场区域(O'为磁场区域的圆心),经磁场偏转后粒子打在磁场下方的平板记录仪AC上.已知磁场区域半径为R,磁感应强度大小为B(方向与纸面垂直),记录仪AC长度为2R,与磁场区域的下边界相切于其中点D.整个装置处于真空中,不计粒子重力,不考虑粒子间的相互作用.
(1)求打在记录板上D点的粒子的比荷;
(2)若氕核(H)恰好打在记录板上D点时,求氚核(H)打在记录板上的位置;
(3)若匀强磁场区域的磁感应强度大小的波动范围为B±ΔB,为使氕核(H)与氚核(H)在记录板上的位置分开,求应满足的条件.
3.[2024·余姚模拟] 清华大学研究的新型SSMB-EUV光刻技术用于提供高强度、可调波长的极紫外光源.方案中的同步轨道如图所示,密度分布非常均匀的稳流电子束被导入同步轨道.同步轨道上存在垂直轨道平面的磁感应强度为B的匀强磁场,电子在磁场控制下沿着固定半径的轨道做匀速圆周运动,每转一周,穿越一次加速腔,从中获得能量,如图所示.同步加速器中磁感应强度随电子速度的增加而增加.已知圆形轨道半径为R,电子的质量为m,电荷量为-e,加速腔ab的长度为L,L R,当电子进入加速腔时,加速电压的大小始终为U,离开加速腔后,加速腔的电压变为0,加速电场的频率与电子的回旋频率保持同步.已知加速腔外无电场,腔内无磁场,不考虑重力、相对论效应以及粒子间相互作用.
(1)当电子在同步轨道中的动能为Ek时,求轨道处的磁感应强度B的大小.
(2)长度为d(d
4.如图所示,有一回旋加速器,两D形盒加上垂直于纸面外、磁感应强度B1可调节的匀强磁场,左盒通过一水平管道与一个左右两侧都开有很小狭缝的圆筒相连,圆筒内有垂直于纸面向内的匀强磁场.现在左盒附近的点S放置一电子,再利用两盒间的狭缝加上一交变电压来给电子周期性加速,经过时间t电子便获得一定速率贴着管壁通过水平管道后进入圆筒,与下圆筒壁发生多次弹性碰撞又不作循环地从圆筒的右狭缝直接离开圆筒.已知圆筒的半径为r,磁感应强度恒为B2,D形盒的半径为R0,电子的比荷为,电子在两D形盒间的狭缝中运动的时间不计,加速电子时电压的大小可视为不变,电子重力不计.
(1)求与下圆筒壁碰撞n次的电子的速率;
(2)由(1)的速率确定D形盒中磁感应强度B1的表达式,并求n=2时B1的值;
(3)若电子在狭缝中加速次数与回旋半周的次数相同,根据n=2时B1的值及其他已知量求加速电压U的值.
参考答案与详细解析
1.(1) (2)
(3)d1
[解析] (1)离子在速度选择器中沿直线运动,则电场力与洛伦兹力平衡,有qv0B1=qE
解得v0=
由几何关系可知,打在感光区域中心P点的离子在分离器中做圆周运动的半径r1=
由洛伦兹力提供向心力,有qv0B2=m
联立解得=
(2)离子在加速电场中加速过程,根据动能定理得qU=m
离子在分离器中做匀速圆周运动,由洛伦兹力提供向心力,有
qv0B2=m
联立可得r=
三种离子的电荷量相同,则质量最小的He做圆周运动的轨迹半径最小,所以(1)中所解比荷对应He.He、He和He三种离子在速度选择器内的磁场中做圆周运动的周期分别为
T1==
T2==
T2==
要使感光板上出现3个有一定宽度的感光区域,三种离子应都能通过速度选择器,三种离子在速度选择器中都应运动整数个周期,则运动时间最小为t0=20T1
所以速度选择器极板的最小长度L=v0t0=.
(3)离子在速度选择器中做圆周运动这一分运动的最大半径为,对三种离子都有===
He在分离器中做匀速圆周运动的最大直径为
Dm1==d1+=d1+×=d1+×
同理,He在分离器中做匀速圆周运动的最小直径为Dm2==d1-×
He在分离器中做匀速圆周运动的最大直径为Dm2'=d1+×
He在分离器中做匀速圆周运动的最小直径为Dm3==d1-×
为能区分3种离子,应满足
Dm1
2.(1) (2)D点右侧距离为R处 (3)≤2-
[解析] (1)当粒子打在记录板上D点时,如图甲所示
根据几何关系可知,粒子在匀强磁场中做匀速圆周运动的半径r=R
粒子在加速电场中加速过程,根据动能定理得qU=mv2
粒子在磁场中做匀速圆周运动,根据洛伦兹力提供向心力可得qvB=m
联立解得=
(2)设H在磁场中做匀速圆周运动的半径为r1,在加速电场中加速过程,根据动能定理得q1U=m1
在磁场中做匀速圆周运动,根据洛伦兹力提供向心力得q1v1B=m1
联立解得r1=
同理,H在磁场中做匀速圆周运动的半径r2=
由于q2=q1,m2=3m1
所以=
H恰好打在记录板上D点,由几何关系可知r1=R
则r2=R
H在磁场中的运动轨迹如图乙所示
由几何关系可知tan =
解得θ=60°
则α=180°-θ=120°
H打在D点右侧与D点的距离为x=Rtan (α-90°)=R
(3)若H在磁感应强度为B-ΔB时与H在磁感应强度为B+ΔB时打在记录板上同一位置,则两粒子的轨迹恰好不重合,此时做匀速圆周运动的半径相等,有
=
解得ΔB=(2-)B
所以应满足的条件为≤2-
3.(1) (2)d (3)
[解析] (1)电子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,有evB=m
又知Ek=mv2
联立解得B=
(2)某次电子束被加速前长度d=v0Δt
其中m=Ek
加速一次过程,由动能定理有eU=m-Ek
电子束被加速一次后长度为d1=v1Δt
联立解得d1=d
(3)注入初动能为Ek、长度为d的电子束,可以被加速腔加速n次,由动能定理有neU=m-Ek
加速后的长度dn=vnΔt
应满足dn≤L
联立解得n≤
即最多可以被加速腔加速次数为
4.(1)tan (n=1,2,3,…)
(2)B1=tan (n=1,2,3,…) (3)
[解析] (1)电子在圆筒中既碰撞又做圆周运动的情形呈现周期性和对称性,作出两种情况为例,如图所示
电子做圆周运动的一个单元夹角θ=(n=1,2,3,…)
由几何关系可知,电子做圆周运动的半径R=rtan θ
由洛伦兹力提供向心力有evB2=m
联立解得电子与下圆筒壁碰撞n次的电子的速率为v=tan (n=1,2,3,…)
(2)电子在回旋加速器中运动刚离开时,由洛伦兹力提供向心力,有eB1v=m
解得B1=tan (n=1,2,3,…)
当n=2时,B1=
(3)电子在回旋加速器中做匀速圆周运动的周期T=
加速的次数为N=
加速N次过程中,由动能定理得N·eU=mv2
当n=2时,v=,B1=
联立解得加速电压为U=
同课章节目录
