2025届高考物理二轮复习:微专题6 电磁场中的空间立体问题和摆线问题-专项训练(含解析)
文档属性
| 名称 | 2025届高考物理二轮复习:微专题6 电磁场中的空间立体问题和摆线问题-专项训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 157.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-05 12:56:19 | ||
图片预览



文档简介
2025届高考物理二轮复习
微专题6 电磁场中的空间立体问题和摆线问题-专项训练
1.离子推进技术在太空探索中已有广泛的应用,其装置可简化为如图甲所示的内、外半径分别为R1和R2的圆筒,图乙为其侧视图.以圆筒左侧圆心O为坐标原点,沿圆筒轴线向右为x轴正方向,建立坐标.在x=0和x=L处垂直于x轴放置栅极,在两圆筒间形成方向沿x轴正方向、电场强度大小为E的匀强电场,同时通过电磁铁在两圆筒间加上沿x轴正方向、磁感应强度大小为B的匀强磁场.待电离的氙原子从左侧栅极飘进两圆筒间(其初速度可视为零).在内圆筒表面分布着沿径向以一定初速度运动的电子源.氙原子被电子碰撞,可电离为一价正离子,刚被电离的氙离子的速度可视为零,经电场加速后从栅极射出,推进器获得反冲力.已知单位时间内刚被电离成氙离子的线密度(沿x轴方向单位长度的离子数)λ=,其中k为常量,氙离子质量为M,电子质量为m,电子电荷量为e,不计离子间、电子间相互作用.
(1)在x处的一个氙原子被电离,求其从右侧栅极射出时的动能;
(2)要使电子不碰到外筒壁,求电子沿径向发射的最大初速度;
(3)若在x~x+Δx的微小区间内被电离的氙离子从右侧栅极射出时所产生的推力为ΔF,求-x的关系式,并画出-x的图像;
(4)求推进器所受的推力.
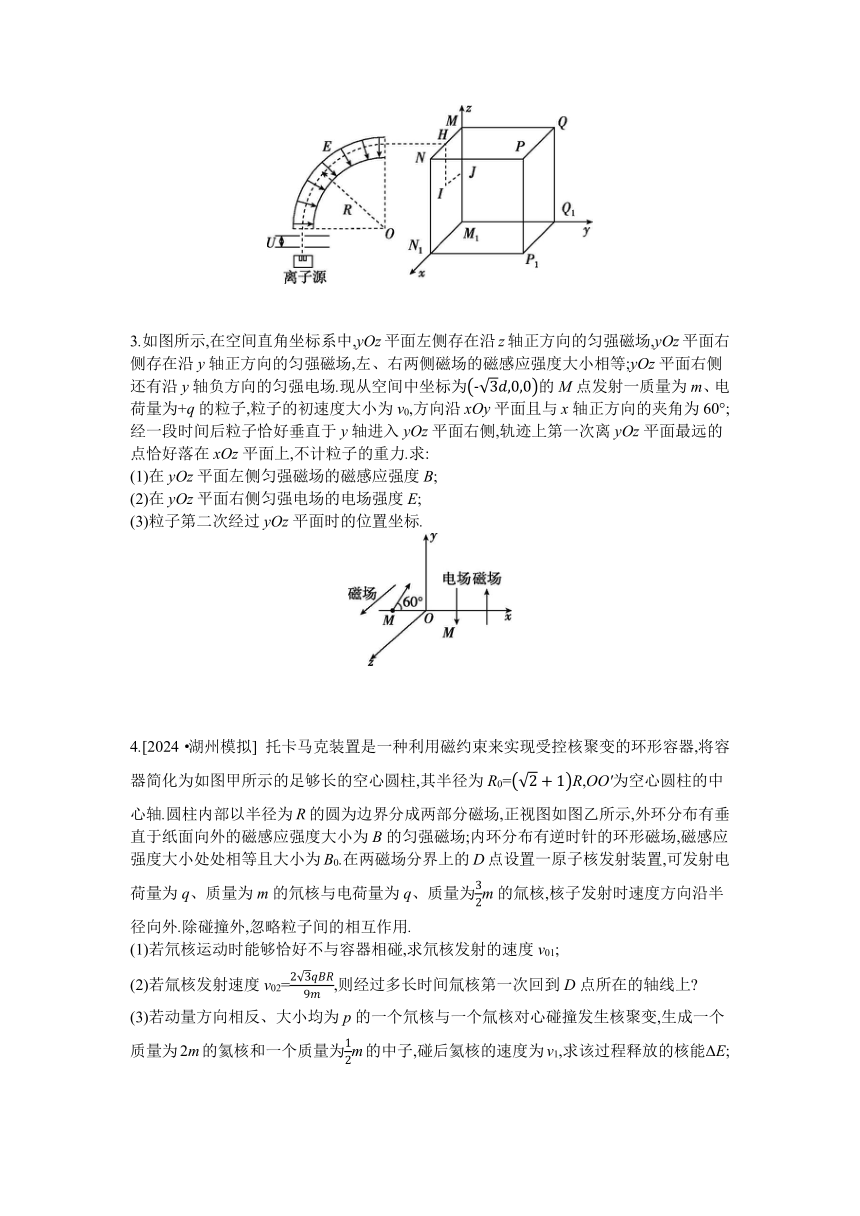
2.[2024·金华模拟] 利用电场与磁场控制带电粒子的运动,在现代科学实验和技术设备中有着广泛的应用.如图所示,一粒子源不断释放质量为m、带电荷量为+q的带电粒子,其初速度视为零,经过加速电压U加速后,以一定速度进入辐向电场,恰好沿着半径为R的圆弧轨迹通过电场区域后垂直于平面MNN1M1射入棱长为2L的正方体区域.现调整射入位置,使带电粒子在边长为L的正方形MHLJ区域内入射,不计粒子重力及其相互作用.
(1)求辐向电场中粒子运动轨迹处电场强度E0的大小;
(2)若仅在正方体区域中加上沿MN方向的匀强电场,要让所有粒子都到达平面NPP1N1,求所加电场强度的最小值E1;
(3)若仅在正方体区域中加上沿MN方向的匀强磁场,要让所有粒子都到达平面M1N1P1Q1,求所加磁感应强度B的大小范围;
(4)以M1为原点,建立如图所示的直角坐标系M1-xyz,若在正方体区域中同时加上沿MN方向、电场强度大小为的匀强电场和第(3)问中磁感应强度范围内最小值的匀强磁场,让粒子对准I点并垂直于平面MNN1M1入射,求粒子离开正方体区域时的位置坐标.
3.如图所示,在空间直角坐标系中,yOz平面左侧存在沿z轴正方向的匀强磁场,yOz平面右侧存在沿y轴正方向的匀强磁场,左、右两侧磁场的磁感应强度大小相等;yOz平面右侧还有沿y轴负方向的匀强电场.现从空间中坐标为的M点发射一质量为m、电荷量为+q的粒子,粒子的初速度大小为v0,方向沿xOy平面且与x轴正方向的夹角为60°;经一段时间后粒子恰好垂直于y轴进入yOz平面右侧,轨迹上第一次离yOz平面最远的点恰好落在xOz平面上,不计粒子的重力.求:
(1)在yOz平面左侧匀强磁场的磁感应强度B;
(2)在yOz平面右侧匀强电场的电场强度E;
(3)粒子第二次经过yOz平面时的位置坐标.
4.[2024·湖州模拟] 托卡马克装置是一种利用磁约束来实现受控核聚变的环形容器,将容器简化为如图甲所示的足够长的空心圆柱,其半径为R0=R,OO'为空心圆柱的中心轴.圆柱内部以半径为R的圆为边界分成两部分磁场,正视图如图乙所示,外环分布有垂直于纸面向外的磁感应强度大小为B的匀强磁场;内环分布有逆时针的环形磁场,磁感应强度大小处处相等且大小为B0.在两磁场分界上的D点设置一原子核发射装置,可发射电荷量为q、质量为m的氘核与电荷量为q、质量为m的氚核,核子发射时速度方向沿半径向外.除碰撞外,忽略粒子间的相互作用.
(1)若氘核运动时能够恰好不与容器相碰,求氘核发射的速度v01;
(2)若氚核发射速度v02=,则经过多长时间氚核第一次回到D点所在的轴线上
(3)若动量方向相反、大小均为p的一个氘核与一个氚核对心碰撞发生核聚变,生成一个质量为2m的氦核和一个质量为m的中子,碰后氦核的速度为v1,求该过程释放的核能ΔE;
(4)假设原子核发射装置只持续稳定发射速度为v02=的氚核,且B0=B,粒子稳定后轴向单位长度内有n个氚核,求圆柱形容器内沿轴线方向的等效电流.
参考答案与详细解析
1.(1)Ee (2)
(3)= 如图所示
(4)L2
[解析] (1)在x处的一个氙原子被电离后从右侧栅极射出时,电场力作用的距离为L-x,由动能定理可知其射出时的动能Ek=Ee(L-x)
(2)电子在筒内垂直于x轴方向上做圆周运动,要使电子不碰到外筒壁,电子沿径向发射速度最大时,电子源应在内圆筒处,则电子运动轨迹如图所示
由几何关系可知=R2+
解得R=
根据洛伦兹力提供向心力,有
evmB=m
解得电子沿径向发射的最大初速度vm=
(3)Δt时间内在x~x+Δx的微小区间内被电离的氙离子个数Δn=λΔtΔx=ΔtΔx
这些氙离子从右侧栅极射出时所产生的推力ΔF==
每个氙离子的动能Ek=Mv2
由(1)知Ek=Ee(L-x)
联立解得=
-x图像如图所示
(4)由图像可知,推进器所受的推力F=×L×L=L2
2.(1) (2) (3)≤B≤ (4)
[解析] (1)粒子经过加速电场加速,根据动能定理有
m-0=Uq
解得v0=
粒子在辐向电场中做匀速圆周运动,由电场力提供向心力,有m=E0q
解得E0=
(2)若仅在正方体区域中加上沿MN方向的匀强电场,则粒子在电场中做类平抛运动,只要从MJ边入射的粒子能够恰好通过PP1边,所有粒子就都能到达平面NPP1N1,由类平抛运动规律可得
qE1=ma
2L=at2
2L=v0t
联立解得E1=
(3)若仅在正方体区域中加上沿MN方向的匀强磁场,则粒子在磁场中做匀速圆周运动,当从MH边射入的粒子恰好到达P1Q1边时,所加的磁场的磁感应强度对应最小值Bmin.
根据几何关系可得r1=2L
由洛伦兹力提供向心力,有qv0Bmin=m
联立解得Bmin=
当从MH边射入的粒子恰好到达M1N1边时,所加的磁场的磁感应强度对应最大值Bmax.
根据几何关系可得r2=L
由洛伦兹力提供向心力,有qv0Bmax=m
联立解得Bmax=
所以磁感应强度B的大小范围是≤B≤
(4)若在正方体区域中同时加上沿MN方向的匀强电场和匀强磁场,则粒子的运动可分解为在平行于yM1z的平面内做圆周运动和在x方向做匀加速直线运动.
如果不考虑x方向的匀加速运动,则粒子在正方体区域中做匀速圆周运动的周期T=
设运动的轨迹对应的圆心角为θ,由几何关系可知r1-r1cos θ=L
解得θ=
所以运动的时间t=T
联立解得t=
如果不考虑平面内的圆周运动,则粒子在正方体区域中做类平抛运动,有
L=a't'2
q·=ma'
联立解得运动的时间t'=L
因为t粒子离开正方体区域时,其x坐标为
x0=L+a't2=L
根据几何关系可知,其y坐标为y0=2Lsin =L
其z坐标为z0=0
所以粒子离开时的坐标为
3.(1) (2)
(3)(0,-3d,4d)
[解析] (1)由几何关系可知,粒子在yOz平面左侧磁场中做匀速圆周运动的半径r1==2d
根据洛伦兹力提供向心力得qv0B=m
联立解得B=
(2)粒子第一次经过y轴后,沿y方向在电场力作用下做匀加速直线运动,同时沿垂直于y轴的平面在洛伦兹力作用下做匀速圆周运动,因轨迹上离yOz平面最远的点恰好落在xOz平面上,可知粒子到达xOz平面上时恰好做个圆周运动,则运动的时间t=
由于yOz左右两侧匀强磁场的磁感应强度大小相等,粒子在左右两侧都是初速度方向垂直于磁场方向,所以粒子在右侧磁场中做圆周运动的半径也为r1,周期T=
沿y方向有r1-r1cos 60°=·t2
联立解得E=
(3)粒子第二次经过yOz平面时在右侧磁场中运动了半个圆周,则所用时间为t'=2t
粒子沿y方向做匀加速直线运动,因在O点上方和下方所用时间相等,可知沿y轴的坐标
y=-3(r1-r1cos 60°)=-3d
沿z轴的坐标z=2r1=4d
所以粒子第二次经过yOz平面时的位置坐标为(0,-3d,4d).
4.(1) (2)+ (3)5m- (4)
[解析] (1)当氘核的轨迹恰好与容器相切时,氘核恰好不与容器相碰,设氘核做匀速圆周运动的半径为r,由几何关系得+r=R0
其中R0=R
联立解得r=R
根据洛伦兹力提供向心力得qv01B=m
解得v01=
(2)设氚核做匀速圆周运动的半径为r',根据洛伦兹力提供向心力得qv02B=m
其中v02=
联立解得r'=R
根据几何关系可知tan=
解得θ=60°
即氚核再次回到内圆边界时,其出射点与入射点对应内圆的圆心角为60°.
氚核沿径向进入内圆,在内圆磁场作用下沿轴向运动半个周期后再次回到内圆边界沿径向飞出,进入外环磁场,然后做周期性的运动,粒子在垂直于轴线的平面内的运动轨迹如图甲所示
粒子沿轴线方向的运动轨迹如图乙所示
氚核在外环中运动的周期
T1==
氚核在内圆中运动的周期
T2==
所以氚核第一次回到D点所在的轴线上需要的时间为t=6×T1+5×T2=+
(3)氘核与氚核的动能分别为Ek2=、Ek3=
由动量守恒定律得2mv1=mvn
解得vn=4v1
该过程释放的核能ΔE=-+=5m-
(4)根据电流的定义式得I==
氚核沿轴线方向的平均速度为=
其中t1=T1,t2=T2
氚核在内圆中做匀速圆周运动,根据洛伦兹力提供向心力得
qv02B0=m
又知v02=,B0=B
联立解得I=.
微专题6 电磁场中的空间立体问题和摆线问题-专项训练
1.离子推进技术在太空探索中已有广泛的应用,其装置可简化为如图甲所示的内、外半径分别为R1和R2的圆筒,图乙为其侧视图.以圆筒左侧圆心O为坐标原点,沿圆筒轴线向右为x轴正方向,建立坐标.在x=0和x=L处垂直于x轴放置栅极,在两圆筒间形成方向沿x轴正方向、电场强度大小为E的匀强电场,同时通过电磁铁在两圆筒间加上沿x轴正方向、磁感应强度大小为B的匀强磁场.待电离的氙原子从左侧栅极飘进两圆筒间(其初速度可视为零).在内圆筒表面分布着沿径向以一定初速度运动的电子源.氙原子被电子碰撞,可电离为一价正离子,刚被电离的氙离子的速度可视为零,经电场加速后从栅极射出,推进器获得反冲力.已知单位时间内刚被电离成氙离子的线密度(沿x轴方向单位长度的离子数)λ=,其中k为常量,氙离子质量为M,电子质量为m,电子电荷量为e,不计离子间、电子间相互作用.
(1)在x处的一个氙原子被电离,求其从右侧栅极射出时的动能;
(2)要使电子不碰到外筒壁,求电子沿径向发射的最大初速度;
(3)若在x~x+Δx的微小区间内被电离的氙离子从右侧栅极射出时所产生的推力为ΔF,求-x的关系式,并画出-x的图像;
(4)求推进器所受的推力.
2.[2024·金华模拟] 利用电场与磁场控制带电粒子的运动,在现代科学实验和技术设备中有着广泛的应用.如图所示,一粒子源不断释放质量为m、带电荷量为+q的带电粒子,其初速度视为零,经过加速电压U加速后,以一定速度进入辐向电场,恰好沿着半径为R的圆弧轨迹通过电场区域后垂直于平面MNN1M1射入棱长为2L的正方体区域.现调整射入位置,使带电粒子在边长为L的正方形MHLJ区域内入射,不计粒子重力及其相互作用.
(1)求辐向电场中粒子运动轨迹处电场强度E0的大小;
(2)若仅在正方体区域中加上沿MN方向的匀强电场,要让所有粒子都到达平面NPP1N1,求所加电场强度的最小值E1;
(3)若仅在正方体区域中加上沿MN方向的匀强磁场,要让所有粒子都到达平面M1N1P1Q1,求所加磁感应强度B的大小范围;
(4)以M1为原点,建立如图所示的直角坐标系M1-xyz,若在正方体区域中同时加上沿MN方向、电场强度大小为的匀强电场和第(3)问中磁感应强度范围内最小值的匀强磁场,让粒子对准I点并垂直于平面MNN1M1入射,求粒子离开正方体区域时的位置坐标.
3.如图所示,在空间直角坐标系中,yOz平面左侧存在沿z轴正方向的匀强磁场,yOz平面右侧存在沿y轴正方向的匀强磁场,左、右两侧磁场的磁感应强度大小相等;yOz平面右侧还有沿y轴负方向的匀强电场.现从空间中坐标为的M点发射一质量为m、电荷量为+q的粒子,粒子的初速度大小为v0,方向沿xOy平面且与x轴正方向的夹角为60°;经一段时间后粒子恰好垂直于y轴进入yOz平面右侧,轨迹上第一次离yOz平面最远的点恰好落在xOz平面上,不计粒子的重力.求:
(1)在yOz平面左侧匀强磁场的磁感应强度B;
(2)在yOz平面右侧匀强电场的电场强度E;
(3)粒子第二次经过yOz平面时的位置坐标.
4.[2024·湖州模拟] 托卡马克装置是一种利用磁约束来实现受控核聚变的环形容器,将容器简化为如图甲所示的足够长的空心圆柱,其半径为R0=R,OO'为空心圆柱的中心轴.圆柱内部以半径为R的圆为边界分成两部分磁场,正视图如图乙所示,外环分布有垂直于纸面向外的磁感应强度大小为B的匀强磁场;内环分布有逆时针的环形磁场,磁感应强度大小处处相等且大小为B0.在两磁场分界上的D点设置一原子核发射装置,可发射电荷量为q、质量为m的氘核与电荷量为q、质量为m的氚核,核子发射时速度方向沿半径向外.除碰撞外,忽略粒子间的相互作用.
(1)若氘核运动时能够恰好不与容器相碰,求氘核发射的速度v01;
(2)若氚核发射速度v02=,则经过多长时间氚核第一次回到D点所在的轴线上
(3)若动量方向相反、大小均为p的一个氘核与一个氚核对心碰撞发生核聚变,生成一个质量为2m的氦核和一个质量为m的中子,碰后氦核的速度为v1,求该过程释放的核能ΔE;
(4)假设原子核发射装置只持续稳定发射速度为v02=的氚核,且B0=B,粒子稳定后轴向单位长度内有n个氚核,求圆柱形容器内沿轴线方向的等效电流.
参考答案与详细解析
1.(1)Ee (2)
(3)= 如图所示
(4)L2
[解析] (1)在x处的一个氙原子被电离后从右侧栅极射出时,电场力作用的距离为L-x,由动能定理可知其射出时的动能Ek=Ee(L-x)
(2)电子在筒内垂直于x轴方向上做圆周运动,要使电子不碰到外筒壁,电子沿径向发射速度最大时,电子源应在内圆筒处,则电子运动轨迹如图所示
由几何关系可知=R2+
解得R=
根据洛伦兹力提供向心力,有
evmB=m
解得电子沿径向发射的最大初速度vm=
(3)Δt时间内在x~x+Δx的微小区间内被电离的氙离子个数Δn=λΔtΔx=ΔtΔx
这些氙离子从右侧栅极射出时所产生的推力ΔF==
每个氙离子的动能Ek=Mv2
由(1)知Ek=Ee(L-x)
联立解得=
-x图像如图所示
(4)由图像可知,推进器所受的推力F=×L×L=L2
2.(1) (2) (3)≤B≤ (4)
[解析] (1)粒子经过加速电场加速,根据动能定理有
m-0=Uq
解得v0=
粒子在辐向电场中做匀速圆周运动,由电场力提供向心力,有m=E0q
解得E0=
(2)若仅在正方体区域中加上沿MN方向的匀强电场,则粒子在电场中做类平抛运动,只要从MJ边入射的粒子能够恰好通过PP1边,所有粒子就都能到达平面NPP1N1,由类平抛运动规律可得
qE1=ma
2L=at2
2L=v0t
联立解得E1=
(3)若仅在正方体区域中加上沿MN方向的匀强磁场,则粒子在磁场中做匀速圆周运动,当从MH边射入的粒子恰好到达P1Q1边时,所加的磁场的磁感应强度对应最小值Bmin.
根据几何关系可得r1=2L
由洛伦兹力提供向心力,有qv0Bmin=m
联立解得Bmin=
当从MH边射入的粒子恰好到达M1N1边时,所加的磁场的磁感应强度对应最大值Bmax.
根据几何关系可得r2=L
由洛伦兹力提供向心力,有qv0Bmax=m
联立解得Bmax=
所以磁感应强度B的大小范围是≤B≤
(4)若在正方体区域中同时加上沿MN方向的匀强电场和匀强磁场,则粒子的运动可分解为在平行于yM1z的平面内做圆周运动和在x方向做匀加速直线运动.
如果不考虑x方向的匀加速运动,则粒子在正方体区域中做匀速圆周运动的周期T=
设运动的轨迹对应的圆心角为θ,由几何关系可知r1-r1cos θ=L
解得θ=
所以运动的时间t=T
联立解得t=
如果不考虑平面内的圆周运动,则粒子在正方体区域中做类平抛运动,有
L=a't'2
q·=ma'
联立解得运动的时间t'=L
因为t
x0=L+a't2=L
根据几何关系可知,其y坐标为y0=2Lsin =L
其z坐标为z0=0
所以粒子离开时的坐标为
3.(1) (2)
(3)(0,-3d,4d)
[解析] (1)由几何关系可知,粒子在yOz平面左侧磁场中做匀速圆周运动的半径r1==2d
根据洛伦兹力提供向心力得qv0B=m
联立解得B=
(2)粒子第一次经过y轴后,沿y方向在电场力作用下做匀加速直线运动,同时沿垂直于y轴的平面在洛伦兹力作用下做匀速圆周运动,因轨迹上离yOz平面最远的点恰好落在xOz平面上,可知粒子到达xOz平面上时恰好做个圆周运动,则运动的时间t=
由于yOz左右两侧匀强磁场的磁感应强度大小相等,粒子在左右两侧都是初速度方向垂直于磁场方向,所以粒子在右侧磁场中做圆周运动的半径也为r1,周期T=
沿y方向有r1-r1cos 60°=·t2
联立解得E=
(3)粒子第二次经过yOz平面时在右侧磁场中运动了半个圆周,则所用时间为t'=2t
粒子沿y方向做匀加速直线运动,因在O点上方和下方所用时间相等,可知沿y轴的坐标
y=-3(r1-r1cos 60°)=-3d
沿z轴的坐标z=2r1=4d
所以粒子第二次经过yOz平面时的位置坐标为(0,-3d,4d).
4.(1) (2)+ (3)5m- (4)
[解析] (1)当氘核的轨迹恰好与容器相切时,氘核恰好不与容器相碰,设氘核做匀速圆周运动的半径为r,由几何关系得+r=R0
其中R0=R
联立解得r=R
根据洛伦兹力提供向心力得qv01B=m
解得v01=
(2)设氚核做匀速圆周运动的半径为r',根据洛伦兹力提供向心力得qv02B=m
其中v02=
联立解得r'=R
根据几何关系可知tan=
解得θ=60°
即氚核再次回到内圆边界时,其出射点与入射点对应内圆的圆心角为60°.
氚核沿径向进入内圆,在内圆磁场作用下沿轴向运动半个周期后再次回到内圆边界沿径向飞出,进入外环磁场,然后做周期性的运动,粒子在垂直于轴线的平面内的运动轨迹如图甲所示
粒子沿轴线方向的运动轨迹如图乙所示
氚核在外环中运动的周期
T1==
氚核在内圆中运动的周期
T2==
所以氚核第一次回到D点所在的轴线上需要的时间为t=6×T1+5×T2=+
(3)氘核与氚核的动能分别为Ek2=、Ek3=
由动量守恒定律得2mv1=mvn
解得vn=4v1
该过程释放的核能ΔE=-+=5m-
(4)根据电流的定义式得I==
氚核沿轴线方向的平均速度为=
其中t1=T1,t2=T2
氚核在内圆中做匀速圆周运动,根据洛伦兹力提供向心力得
qv02B0=m
又知v02=,B0=B
联立解得I=.
同课章节目录
