2025届高考物理二轮复习:专题二 功和能、动量 第4讲 功、功率、动能定理-专项训练(含解析)
文档属性
| 名称 | 2025届高考物理二轮复习:专题二 功和能、动量 第4讲 功、功率、动能定理-专项训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 113.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-05 12:57:32 | ||
图片预览

文档简介
2025届高考物理二轮复习
专题二 功和能、动量 第4讲 功、功率、动能定理-专项训练
1.[2024·温岭模拟] 如图所示是某地铁中的列车从左向右匀速率通过轨道abcd的示意图,其中bc段水平,ab与cd段的倾角相等.已知整个过程中列车受到的阻力大小保持不变(包括摩擦阻力和空气阻力),在ab和bc段列车牵引力的功率分别为P1和P2,则在cd段列车牵引力的功率为( )
A.2P2-P1
B.P2-P1
C.
D.
2.[2024·新课标卷] 福建舰是我国自主设计建造的首艘弹射型航空母舰.借助配重小车可以进行弹射测试,测试时配重小车被弹射器从甲板上水平弹出后,落到海面上.调整弹射装置,使小车水平离开甲板时的动能变为调整前的4倍.忽略空气阻力,则小车在海面上的落点与其离开甲板处的水平距离为调整前的 ( )
A.0.25倍 B.0.5倍
C.2倍 D.4倍
3.无风时,雨滴受空气阻力的作用在地面附近会以恒定的速率竖直下落.一质量为m的雨滴在地面附近以速率v下落高度h的过程中(重力加速度大小为g),克服空气阻力做的功为 ( )
A.0 B.mgh
C.mv2-mgh D.mv2+mgh
4.[2024·温州模拟] 我国无人机技术发展迅猛,应用也越来越广泛,无人机配送快递就是一种全新的配送方式.如图所示,一架配送包裹的无人机从地面起飞后竖直上升的过程中,升力的功率恒为P0.已知无人机的质量与包裹的质量的比值为k,忽略空气阻力的影响,则该过程中悬吊包裹的轻绳(不可伸长)对包裹做功的功率为 ( )
A.
B.
C.
D.
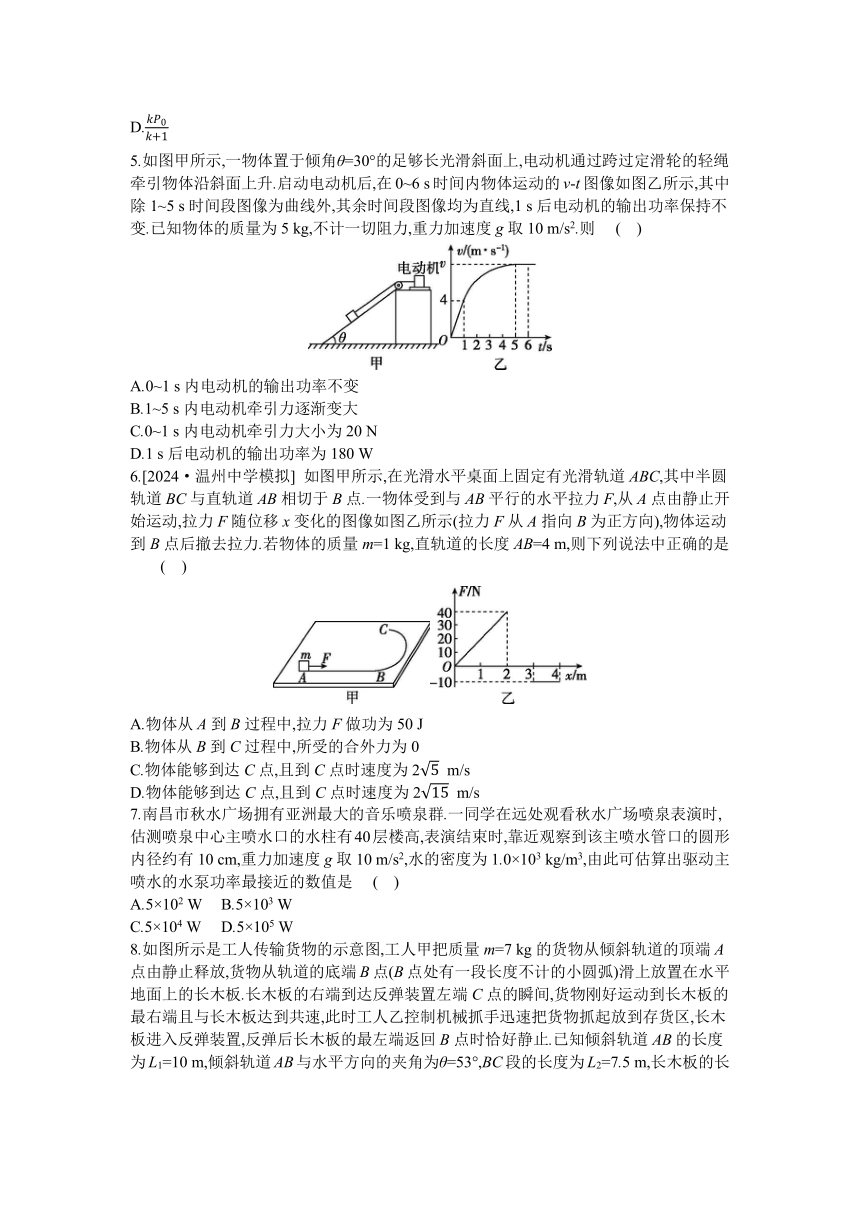
5.如图甲所示,一物体置于倾角θ=30°的足够长光滑斜面上,电动机通过跨过定滑轮的轻绳牵引物体沿斜面上升.启动电动机后,在0~6 s时间内物体运动的v-t图像如图乙所示,其中除1~5 s时间段图像为曲线外,其余时间段图像均为直线,1 s后电动机的输出功率保持不变.已知物体的质量为5 kg,不计一切阻力,重力加速度g取10 m/s2.则 ( )
A.0~1 s内电动机的输出功率不变
B.1~5 s内电动机牵引力逐渐变大
C.0~1 s内电动机牵引力大小为20 N
D.1 s后电动机的输出功率为180 W
6.[2024·温州中学模拟] 如图甲所示,在光滑水平桌面上固定有光滑轨道ABC,其中半圆轨道BC与直轨道AB相切于B点.一物体受到与AB平行的水平拉力F,从A点由静止开始运动,拉力F随位移x变化的图像如图乙所示(拉力F从A指向B为正方向),物体运动到B点后撤去拉力.若物体的质量m=1 kg,直轨道的长度AB=4 m,则下列说法中正确的是 ( )
A.物体从A到B过程中,拉力F做功为50 J
B.物体从B到C过程中,所受的合外力为0
C.物体能够到达C点,且到C点时速度为2 m/s
D.物体能够到达C点,且到C点时速度为2 m/s
7.南昌市秋水广场拥有亚洲最大的音乐喷泉群.一同学在远处观看秋水广场喷泉表演时,估测喷泉中心主喷水口的水柱有40层楼高,表演结束时,靠近观察到该主喷水管口的圆形内径约有10 cm,重力加速度g取10 m/s2,水的密度为1.0×103 kg/m3,由此可估算出驱动主喷水的水泵功率最接近的数值是 ( )
A.5×102 W B.5×103 W
C.5×104 W D.5×105 W
8.如图所示是工人传输货物的示意图,工人甲把质量m=7 kg的货物从倾斜轨道的顶端A点由静止释放,货物从轨道的底端B点(B点处有一段长度不计的小圆弧)滑上放置在水平地面上的长木板.长木板的右端到达反弹装置左端C点的瞬间,货物刚好运动到长木板的最右端且与长木板达到共速,此时工人乙控制机械抓手迅速把货物抓起放到存货区,长木板进入反弹装置,反弹后长木板的最左端返回B点时恰好静止.已知倾斜轨道AB的长度为L1=10 m,倾斜轨道AB与水平方向的夹角为θ=53°,BC段的长度为L2=7.5 m,长木板的长度为d=5 m,货物与倾斜轨道以及长木板间的动摩擦因数均为μ1=0.5,长木板与地面间的动摩擦因数为μ2=0.2,重力加速度g取10 m/s2,sin 53°=0.8,cos 53°=0.6.
(1)货物到达B点时的速度vB为多大
(2)长木板的右端刚到C点时货物的速度vC为多大
(3)长木板在反弹过程中损失的能量与长木板刚接触反弹装置时的能量的比值η为多少
9.[2024·诸暨模拟] 如图所示,可视为质点的质量为m=0.1 kg的小滑块静止在水平轨道上的A点,在水平向右的恒定拉力F的作用下,滑块从A点开始做匀加速直线运动,在滑块运动到水平轨道AB之间某一点时撤去拉力,滑块继续运动到B点后进入半径为R=0.4 m且内壁光滑的竖直固定圆管道,在圆管道中运行一周后从C处的出口出来后向D点滑动,D点右侧有一与CD等高的传送带紧靠D点且平滑连接,并以恒定的速度v=3 m/s顺时针转动.已知水平轨道AB光滑,小滑块与水平轨道CD间的动摩擦因数为μ1=0.2,小滑块与传送带间的动摩擦因数μ2=0.5,AB的长度为l1=1.0 m,CD的长度为l2=3.5 m,DE段传送带的长度为l3=0.5 m,重力加速度g取10 m/s2.
(1)若滑块恰能过圆管道的最高点,求滑块刚运动到B点时对圆管道的压力;
(2)若滑块到AB中点时撤去拉力,为使小滑块能到达传送带左侧D点,求F最小值;
(3)若在AB段水平拉力F=2 N且作用距离x可变,滑块到D点后一直在传送带上加速运动,且到E点时速度小于3 m/s,试求小滑块到达传送带右侧E点时的速度v与水平拉力F的作用距离x的关系.
参考答案与详细解析
1.A [解析] 列车在三个路段均做匀速直线运动,在ab段,由平衡条件得+mgsin θ-Ff=0,在bc段,由平衡条件得-Ff=0,在cd段,由平衡条件得-mgsin θ-Ff=0,联立解得P3=2P2-P1,故A正确.
2.C [解析] 动能表达式为Ek=mv2,使小车水平离开甲板时的动能变为调整前的4倍,则小车离开甲板时的速度变为调整前的2倍;小车离开甲板后做平抛运动,根据h=gt2可知,从离开甲板至到达海面所用的时间不变,根据x=vt可知,小车在海面上的落点与其离开甲板处的水平距离为调整前的2倍,故C正确.
3.B [解析] 地面附近的雨滴下落过程中做匀速直线运动,根据动能定理得mgh-Wf=0,故雨滴克服空气阻力做功为mgh,故B正确.
4.B [解析] 对无人机和包裹整体,由动能定理可得P0t-(m机+m物)gh=(m机+m物)v2,对包裹,由动能定理可得Pt-m物gh=m物v2,已知=k,联立解得P=,故B正确.
5.D [解析] 由图可知,0~1 s物体做匀加速直线运动,则电动机牵引力大小不变,物体速度增大,则0~1 s电动机的输出功率变大,A错误;由图可知,1~5 s内物体的加速度逐渐减小,则电动机牵引力逐渐减小,B错误;由图可知,0~1 s内物体的加速度为a= m/s2=4 m/s2,由牛顿第二定律可得,0~1 s内电动机牵引力大小为F=ma+mgsin θ=45 N,C错误;1 s后电动机的输出功率不变,等于1 s时的输出功率,则有P=Fv=45×4 W=180 W,D正确.
6.D [解析] F-x图像与横坐标轴所围面积表示功,由图像可知,物体从A到B过程中,拉力F做功为W=×40×2 J-10×1 J=30 J,故A错误;物体从B到C过程中,做圆周运动,所受的合外力不为0,故B错误;物体从A到B过程中,由动能定理有W=m,解得vB=2 m/s ,由于光滑轨道ABC在水平面内,物体从B到C做匀速圆周运动,所以物体能够到达C点,且到C点时速度为2 m/s,故C错误,D正确.
7.D [解析] 40层楼高约为h=120 m,设水泵的功率为P,水泵在时间Δt内使质量为Δm的水以速度v通过喷水管口,由动能定理得PΔt=Δmv2,由运动学公式得v2=2gh,其中Δm=ρSvΔt,S=πD2,联立可得P=πD2ρgh≈5×105 W,故D正确.
8.(1)10 m/s (2)5 m/s (3)0.6
[解析] (1)货物由A点运动到B点过程,根据动能定理
可得mgL1sin 53°-μ1mgL1cos 53°=m
解得vB=10 m/s
(2)货物在长木板上做匀减速直线运动,由牛顿第二定律可得μ1mg=ma货
根据匀变速直线运动规律得-2a货L2=-
联立解得vC=5 m/s
(3)长木板进入反弹装置时的速度v1=vC
设长木板的质量为M,则长木板刚进入反弹装置时的能量为E=M
设长木板反弹后右端回到C点时的速度为v2,长木板从右端反弹回到C点至左端回到B点的过程中,由动能定理可得-μ2Mg(L2-d)=0-M
长木板在反弹的过程中损失的能量为ΔE=M-M
所以长木板在反弹过程中损失的能量与长木板刚接触反弹装置时的能量的比值η=
联立解得η=0.6
9.(1)5 N,方向竖直向下 (2)1.6 N (3)v=(m/s),其中0.4 m≤x<0.45 m
[解析] (1)若滑块恰能过圆管道的最高点,则滑块在圆管道的最高点时的速度为零.
滑块由B点运动到圆管道的最高点的过程,由机械能守恒定律得-2mgR=0-m
滑块在B点时,根据牛顿第二定律有FNB-mg=m
联立解得FNB=5 N
根据牛顿第三定律可知,滑块刚到B点时对圆管道的压力大小为FNB压=FNB=5 N,方向竖直向下.
(2)若滑块恰能过圆管道的最高点,则滑块由A点运动到圆管道的最高点的过程,由动能定理得F1-2mgR=0
解得F1=1.6 N
若滑块恰能到D点,则滑块由A点运动到D点的过程,由动能定理得F2-μ1mgl2=0
解得F2=1.4 N
综上所述,F的最小值为1.6 N.
(3)滑块一定过圆管道的最高点,由动能定理得Fx1-2mgR=0
解得x1=0.4 m
滑块到D点后一直在传送带上加速运动,且到E点时速度小于3 m/s,由动能定理得Fx-μ1mgl2+μ2mgl3=mv2
且v<3 m/s
解得v=(m/s),x<0.45 m
综上所述,v=(m/s),其中0.4 m≤x<0.45 m.
专题二 功和能、动量 第4讲 功、功率、动能定理-专项训练
1.[2024·温岭模拟] 如图所示是某地铁中的列车从左向右匀速率通过轨道abcd的示意图,其中bc段水平,ab与cd段的倾角相等.已知整个过程中列车受到的阻力大小保持不变(包括摩擦阻力和空气阻力),在ab和bc段列车牵引力的功率分别为P1和P2,则在cd段列车牵引力的功率为( )
A.2P2-P1
B.P2-P1
C.
D.
2.[2024·新课标卷] 福建舰是我国自主设计建造的首艘弹射型航空母舰.借助配重小车可以进行弹射测试,测试时配重小车被弹射器从甲板上水平弹出后,落到海面上.调整弹射装置,使小车水平离开甲板时的动能变为调整前的4倍.忽略空气阻力,则小车在海面上的落点与其离开甲板处的水平距离为调整前的 ( )
A.0.25倍 B.0.5倍
C.2倍 D.4倍
3.无风时,雨滴受空气阻力的作用在地面附近会以恒定的速率竖直下落.一质量为m的雨滴在地面附近以速率v下落高度h的过程中(重力加速度大小为g),克服空气阻力做的功为 ( )
A.0 B.mgh
C.mv2-mgh D.mv2+mgh
4.[2024·温州模拟] 我国无人机技术发展迅猛,应用也越来越广泛,无人机配送快递就是一种全新的配送方式.如图所示,一架配送包裹的无人机从地面起飞后竖直上升的过程中,升力的功率恒为P0.已知无人机的质量与包裹的质量的比值为k,忽略空气阻力的影响,则该过程中悬吊包裹的轻绳(不可伸长)对包裹做功的功率为 ( )
A.
B.
C.
D.
5.如图甲所示,一物体置于倾角θ=30°的足够长光滑斜面上,电动机通过跨过定滑轮的轻绳牵引物体沿斜面上升.启动电动机后,在0~6 s时间内物体运动的v-t图像如图乙所示,其中除1~5 s时间段图像为曲线外,其余时间段图像均为直线,1 s后电动机的输出功率保持不变.已知物体的质量为5 kg,不计一切阻力,重力加速度g取10 m/s2.则 ( )
A.0~1 s内电动机的输出功率不变
B.1~5 s内电动机牵引力逐渐变大
C.0~1 s内电动机牵引力大小为20 N
D.1 s后电动机的输出功率为180 W
6.[2024·温州中学模拟] 如图甲所示,在光滑水平桌面上固定有光滑轨道ABC,其中半圆轨道BC与直轨道AB相切于B点.一物体受到与AB平行的水平拉力F,从A点由静止开始运动,拉力F随位移x变化的图像如图乙所示(拉力F从A指向B为正方向),物体运动到B点后撤去拉力.若物体的质量m=1 kg,直轨道的长度AB=4 m,则下列说法中正确的是 ( )
A.物体从A到B过程中,拉力F做功为50 J
B.物体从B到C过程中,所受的合外力为0
C.物体能够到达C点,且到C点时速度为2 m/s
D.物体能够到达C点,且到C点时速度为2 m/s
7.南昌市秋水广场拥有亚洲最大的音乐喷泉群.一同学在远处观看秋水广场喷泉表演时,估测喷泉中心主喷水口的水柱有40层楼高,表演结束时,靠近观察到该主喷水管口的圆形内径约有10 cm,重力加速度g取10 m/s2,水的密度为1.0×103 kg/m3,由此可估算出驱动主喷水的水泵功率最接近的数值是 ( )
A.5×102 W B.5×103 W
C.5×104 W D.5×105 W
8.如图所示是工人传输货物的示意图,工人甲把质量m=7 kg的货物从倾斜轨道的顶端A点由静止释放,货物从轨道的底端B点(B点处有一段长度不计的小圆弧)滑上放置在水平地面上的长木板.长木板的右端到达反弹装置左端C点的瞬间,货物刚好运动到长木板的最右端且与长木板达到共速,此时工人乙控制机械抓手迅速把货物抓起放到存货区,长木板进入反弹装置,反弹后长木板的最左端返回B点时恰好静止.已知倾斜轨道AB的长度为L1=10 m,倾斜轨道AB与水平方向的夹角为θ=53°,BC段的长度为L2=7.5 m,长木板的长度为d=5 m,货物与倾斜轨道以及长木板间的动摩擦因数均为μ1=0.5,长木板与地面间的动摩擦因数为μ2=0.2,重力加速度g取10 m/s2,sin 53°=0.8,cos 53°=0.6.
(1)货物到达B点时的速度vB为多大
(2)长木板的右端刚到C点时货物的速度vC为多大
(3)长木板在反弹过程中损失的能量与长木板刚接触反弹装置时的能量的比值η为多少
9.[2024·诸暨模拟] 如图所示,可视为质点的质量为m=0.1 kg的小滑块静止在水平轨道上的A点,在水平向右的恒定拉力F的作用下,滑块从A点开始做匀加速直线运动,在滑块运动到水平轨道AB之间某一点时撤去拉力,滑块继续运动到B点后进入半径为R=0.4 m且内壁光滑的竖直固定圆管道,在圆管道中运行一周后从C处的出口出来后向D点滑动,D点右侧有一与CD等高的传送带紧靠D点且平滑连接,并以恒定的速度v=3 m/s顺时针转动.已知水平轨道AB光滑,小滑块与水平轨道CD间的动摩擦因数为μ1=0.2,小滑块与传送带间的动摩擦因数μ2=0.5,AB的长度为l1=1.0 m,CD的长度为l2=3.5 m,DE段传送带的长度为l3=0.5 m,重力加速度g取10 m/s2.
(1)若滑块恰能过圆管道的最高点,求滑块刚运动到B点时对圆管道的压力;
(2)若滑块到AB中点时撤去拉力,为使小滑块能到达传送带左侧D点,求F最小值;
(3)若在AB段水平拉力F=2 N且作用距离x可变,滑块到D点后一直在传送带上加速运动,且到E点时速度小于3 m/s,试求小滑块到达传送带右侧E点时的速度v与水平拉力F的作用距离x的关系.
参考答案与详细解析
1.A [解析] 列车在三个路段均做匀速直线运动,在ab段,由平衡条件得+mgsin θ-Ff=0,在bc段,由平衡条件得-Ff=0,在cd段,由平衡条件得-mgsin θ-Ff=0,联立解得P3=2P2-P1,故A正确.
2.C [解析] 动能表达式为Ek=mv2,使小车水平离开甲板时的动能变为调整前的4倍,则小车离开甲板时的速度变为调整前的2倍;小车离开甲板后做平抛运动,根据h=gt2可知,从离开甲板至到达海面所用的时间不变,根据x=vt可知,小车在海面上的落点与其离开甲板处的水平距离为调整前的2倍,故C正确.
3.B [解析] 地面附近的雨滴下落过程中做匀速直线运动,根据动能定理得mgh-Wf=0,故雨滴克服空气阻力做功为mgh,故B正确.
4.B [解析] 对无人机和包裹整体,由动能定理可得P0t-(m机+m物)gh=(m机+m物)v2,对包裹,由动能定理可得Pt-m物gh=m物v2,已知=k,联立解得P=,故B正确.
5.D [解析] 由图可知,0~1 s物体做匀加速直线运动,则电动机牵引力大小不变,物体速度增大,则0~1 s电动机的输出功率变大,A错误;由图可知,1~5 s内物体的加速度逐渐减小,则电动机牵引力逐渐减小,B错误;由图可知,0~1 s内物体的加速度为a= m/s2=4 m/s2,由牛顿第二定律可得,0~1 s内电动机牵引力大小为F=ma+mgsin θ=45 N,C错误;1 s后电动机的输出功率不变,等于1 s时的输出功率,则有P=Fv=45×4 W=180 W,D正确.
6.D [解析] F-x图像与横坐标轴所围面积表示功,由图像可知,物体从A到B过程中,拉力F做功为W=×40×2 J-10×1 J=30 J,故A错误;物体从B到C过程中,做圆周运动,所受的合外力不为0,故B错误;物体从A到B过程中,由动能定理有W=m,解得vB=2 m/s ,由于光滑轨道ABC在水平面内,物体从B到C做匀速圆周运动,所以物体能够到达C点,且到C点时速度为2 m/s,故C错误,D正确.
7.D [解析] 40层楼高约为h=120 m,设水泵的功率为P,水泵在时间Δt内使质量为Δm的水以速度v通过喷水管口,由动能定理得PΔt=Δmv2,由运动学公式得v2=2gh,其中Δm=ρSvΔt,S=πD2,联立可得P=πD2ρgh≈5×105 W,故D正确.
8.(1)10 m/s (2)5 m/s (3)0.6
[解析] (1)货物由A点运动到B点过程,根据动能定理
可得mgL1sin 53°-μ1mgL1cos 53°=m
解得vB=10 m/s
(2)货物在长木板上做匀减速直线运动,由牛顿第二定律可得μ1mg=ma货
根据匀变速直线运动规律得-2a货L2=-
联立解得vC=5 m/s
(3)长木板进入反弹装置时的速度v1=vC
设长木板的质量为M,则长木板刚进入反弹装置时的能量为E=M
设长木板反弹后右端回到C点时的速度为v2,长木板从右端反弹回到C点至左端回到B点的过程中,由动能定理可得-μ2Mg(L2-d)=0-M
长木板在反弹的过程中损失的能量为ΔE=M-M
所以长木板在反弹过程中损失的能量与长木板刚接触反弹装置时的能量的比值η=
联立解得η=0.6
9.(1)5 N,方向竖直向下 (2)1.6 N (3)v=(m/s),其中0.4 m≤x<0.45 m
[解析] (1)若滑块恰能过圆管道的最高点,则滑块在圆管道的最高点时的速度为零.
滑块由B点运动到圆管道的最高点的过程,由机械能守恒定律得-2mgR=0-m
滑块在B点时,根据牛顿第二定律有FNB-mg=m
联立解得FNB=5 N
根据牛顿第三定律可知,滑块刚到B点时对圆管道的压力大小为FNB压=FNB=5 N,方向竖直向下.
(2)若滑块恰能过圆管道的最高点,则滑块由A点运动到圆管道的最高点的过程,由动能定理得F1-2mgR=0
解得F1=1.6 N
若滑块恰能到D点,则滑块由A点运动到D点的过程,由动能定理得F2-μ1mgl2=0
解得F2=1.4 N
综上所述,F的最小值为1.6 N.
(3)滑块一定过圆管道的最高点,由动能定理得Fx1-2mgR=0
解得x1=0.4 m
滑块到D点后一直在传送带上加速运动,且到E点时速度小于3 m/s,由动能定理得Fx-μ1mgl2+μ2mgl3=mv2
且v<3 m/s
解得v=(m/s),x<0.45 m
综上所述,v=(m/s),其中0.4 m≤x<0.45 m.
同课章节目录
