2025届高考物理二轮复习:第10讲 电磁感应-专项训练 (含解析)
文档属性
| 名称 | 2025届高考物理二轮复习:第10讲 电磁感应-专项训练 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 197.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-05 13:09:58 | ||
图片预览


文档简介
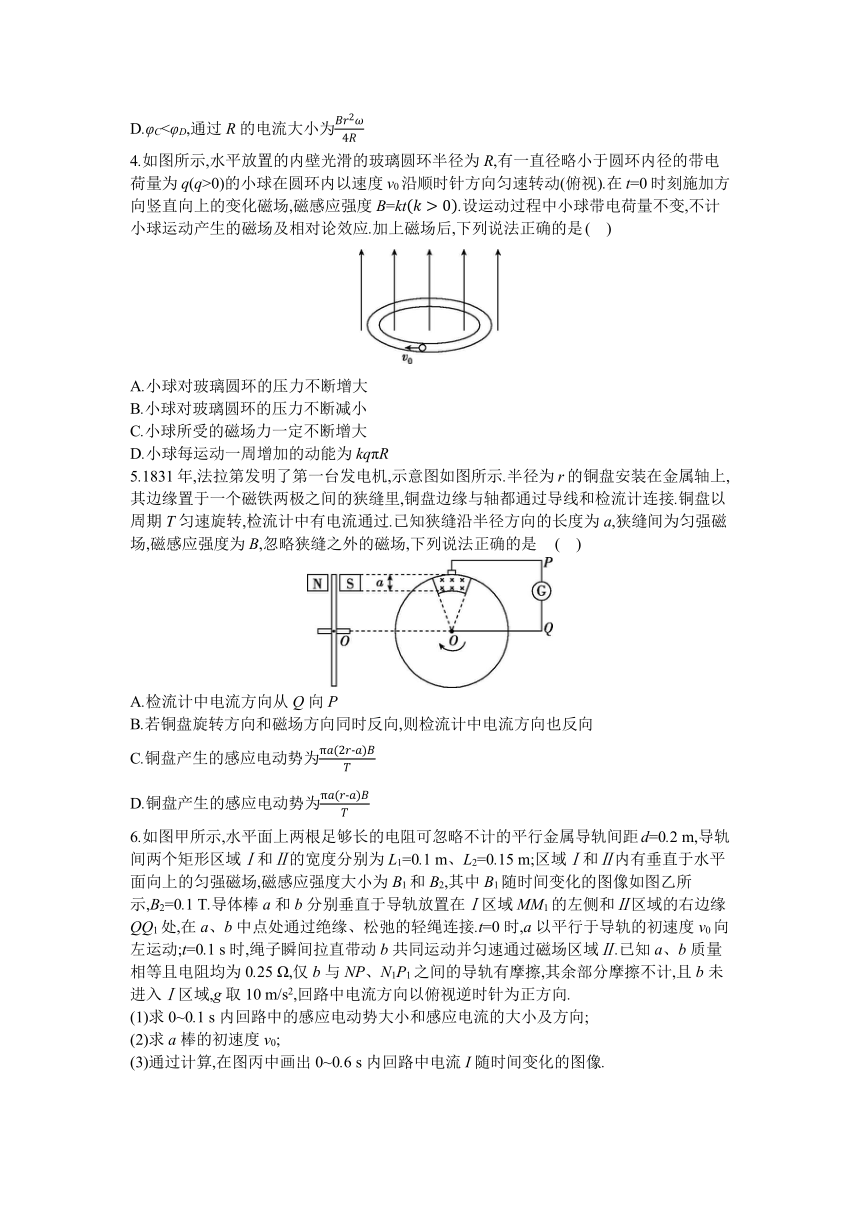
2025届高考物理二轮复习:第10讲 电磁感应-专项训练
1.[2023·湖北卷] 近场通信(NFC)器件应用电磁感应原理进行通讯.其天线类似一个压平的线圈,线圈尺寸从内到外逐渐变大.如图所示,一正方形NFC线圈共3匝,其边长分别为1.0 cm、1.2 cm和1.4 cm.图中线圈外线接入内部芯片时与内部线圈绝缘.若匀强磁场垂直通过此线圈,磁感应强度变化率为103 T/s,则线圈产生的感应电动势最接近( )
A.0.30 V
B.0.44 V
C.0.59 V
D.4.3 V
2.如图所示,在同一个水平面内有彼此绝缘的两个光滑圆环A、B,大圆环A中有顺时针方向的恒定电流I,小圆环B的一半面积在环A内、一半面积在环A外,下列说法正确的是 ( )
A.穿过环B的磁通量为0
B.环B中有持续的感应电流
C.若增大环A内的电流,则环B会向右移动
D.若减小环A内的电流,则环B会产生逆时针方向的感应电流
3.图甲中有一水平向右的匀强磁场,将一个水平放置的金属棒ab以某一水平速度抛出,金属棒在运动过程中始终保持水平,不计空气阻力,金属棒在运动过程中ab两端的电势分别为φa、φb;图乙为法拉第圆盘发电机的原理图,水平匀强磁场垂直于盘面,圆盘绕水平轴C以角速度ω匀速转动,铜片D与圆盘的边缘接触,圆盘、导线和电阻R组成闭合回路,圆盘半径为r,圆盘接入的电阻也为R,其他电阻均可忽略不计,CD两端的电势分别为φC、φD.下列说法正确的是 ( )
A.φa>φb,且a、b两端电势差Uab保持不变
B.φa<φb,且b、a两端电势差Uba逐渐增大
C.φC>φD,且C、D两端电势差UCD=Br2ω
D.φC<φD,通过R的电流大小为
4.如图所示,水平放置的内壁光滑的玻璃圆环半径为R,有一直径略小于圆环内径的带电荷量为q(q>0)的小球在圆环内以速度v0沿顺时针方向匀速转动(俯视).在t=0时刻施加方向竖直向上的变化磁场,磁感应强度B=kt.设运动过程中小球带电荷量不变,不计小球运动产生的磁场及相对论效应.加上磁场后,下列说法正确的是 ( )
A.小球对玻璃圆环的压力不断增大
B.小球对玻璃圆环的压力不断减小
C.小球所受的磁场力一定不断增大
D.小球每运动一周增加的动能为kqπR
5.1831年,法拉第发明了第一台发电机,示意图如图所示.半径为r的铜盘安装在金属轴上,其边缘置于一个磁铁两极之间的狭缝里,铜盘边缘与轴都通过导线和检流计连接.铜盘以周期T匀速旋转,检流计中有电流通过.已知狭缝沿半径方向的长度为a,狭缝间为匀强磁场,磁感应强度为B,忽略狭缝之外的磁场,下列说法正确的是 ( )
A.检流计中电流方向从Q向P
B.若铜盘旋转方向和磁场方向同时反向,则检流计中电流方向也反向
C.铜盘产生的感应电动势为
D.铜盘产生的感应电动势为
6.如图甲所示,水平面上两根足够长的电阻可忽略不计的平行金属导轨间距d=0.2 m,导轨间两个矩形区域Ⅰ和Ⅱ的宽度分别为L1=0.1 m、L2=0.15 m;区域Ⅰ和Ⅱ内有垂直于水平面向上的匀强磁场,磁感应强度大小为B1和B2,其中B1随时间变化的图像如图乙所示,B2=0.1 T.导体棒a和b分别垂直于导轨放置在Ⅰ区域MM1的左侧和Ⅱ区域的右边缘QQ1处,在a、b中点处通过绝缘、松弛的轻绳连接.t=0时,a以平行于导轨的初速度v0向左运动;t=0.1 s时,绳子瞬间拉直带动b共同运动并匀速通过磁场区域Ⅱ.已知a、b质量相等且电阻均为0.25 Ω,仅b与NP、N1P1之间的导轨有摩擦,其余部分摩擦不计,且b未进入Ⅰ区域,g取10 m/s2,回路中电流方向以俯视逆时针为正方向.
(1)求0~0.1 s内回路中的感应电动势大小和感应电流的大小及方向;
(2)求a棒的初速度v0;
(3)通过计算,在图丙中画出0~0.6 s内回路中电流I随时间变化的图像.
7.如图所示,在水平面内有一圆柱形轨道,虚线MN将轨道分为左右两部分,左侧轨道光滑且处于垂直于圆柱外表面的辐向磁场中,右侧粗糙且处于平行于圆柱轴线的匀强电场中.外表面绝缘的导体圆环P套在导轨上位于左端的弹射器内,某时刻弹射器给P一冲量I=14 N·s,将P弹射进入辐向磁场,P向右运动一段时间在边界MN处与绝缘带电圆环Q发生弹性碰撞,碰撞过程中Q带的电荷量不变,碰后P反弹进入磁场,Q则进入右侧电场中,在电场右侧轨道上存在挡板,Q与挡板碰后反弹,碰撞时间极短,碰后损失25%的机械能.已知P、Q两圆环的直径略大于轨道的直径,磁场区域长度为x1=2 m,P、Q两圆环周长均为L=1.0 m,P的质量m1=1 kg,P的电阻R=0.1 Ω,Q的质量m2=2 kg,Q带电荷量q=0.5 C,Q环在虚线MN右侧受到摩擦阻力Ff=6 N,圆环所在位置磁感应强度B=0.5 T,电场强度E=20 N/C,右侧的挡板到MN的距离为x2=3 m.
(1)求P环刚弹射入磁场时的加速度.
(2)P环与Q环碰后能否返回弹射器 若能,请求出返回弹射器时的速度大小;若不能,请求出P环停止时离MN的距离.
(3)求Q环在电场中运动的总路程.
参考答案与详细解析
1.B [解析] 根据法拉第电磁感应定律可知E==S=103×(1.02+1.22+1.42)×10-4 V=0.44 V,故B正确.
2.C [解析] 根据安培定则可知,环A上的电流在其内部产生的磁场均向里,在环B左半圆环内磁场垂直于纸面向里,右半圆环内磁场垂直于纸面向外,因为小圆环B在环A内部的磁场比外部的强,根据磁通量的概念可知,小圆环B在环A内部分的磁通量(向内)大于在环A外部分的磁通量(向外),所以穿过小圆环B的磁通量不为0,且磁通量指向纸面内,故A错误;由于环A中通有恒定电流I,则环B中磁通量不变,无感应电流,故B错误;若增大环A内的电流,则环B内的磁通量向里增加,根据楞次定律,为了阻碍磁通量的增加,环B会向右移动,故C正确;若减小环A内的电流,则环B内的磁通量向里减小,根据楞次定律可判断出,环B会产生顺时针方向的感应电流,故D错误.
3.D [解析] 金属棒ab做平抛运动,竖直方向的分速度与磁感线垂直,根据右手定则可知a点电势高于b点电势,即φa>φb,根据法拉第电磁感应定律得Uab=BLvy=BLgt,即Uab逐渐增大,故A、B错误;圆盘转动过程中,根据右手定则可知D点电势高于C点电势,即φC<φD,由法拉第电磁感应定律可得圆盘产生的感应电动势为E=Br2ω,通过R的电流大小为I==,C、D两端电势差为UCD=-IR=-Br2ω,故C错误,D正确.
4.C [解析] 由楞次定律可判断出,当磁场增强时,会产生顺时针方向的涡旋电场,电场力对小球做正功,使其沿顺时针方向做加速运动,根据牛顿第二定律可知,未加磁场时,圆环对小球的压力FN=m,加磁场后,根据左手定则可知,小球所受的洛伦兹力方向指向圆心,圆环对小球的压力与洛伦兹力的合力提供向心力,由于不确定洛伦兹力与向心力的大小关系,所以小球与圆环之间的弹力变化情况不明,故A、B错误;根据F洛=qvB,由于v与B都增大,所以小球所受的磁场力一定不断增大,故C正确;由动能定理可得W电=ΔEk,小球每运动一周,电场力做功为W电=qU,其中U=·πR2=kπR2,联立解得ΔEk=kπqR2,故D错误.
5.C [解析] 根据右手定则可知,检流计中电流方向从P向Q,若铜盘旋转方向和磁场方向同时反向,则检流计中电流方向不变,故A、B错误;铜盘产生的感应电动势为E=Ba=,故C正确,D错误.
6.(1)0.01 V 0.02 A 负方向
(2)1 m/s (3)如图所示
[解析] (1)由图乙可知,0~0.1 s内,=0.5 T/s
则回路中的感生电动势E1==L1d=0.01 V
回路中的感应电流I1==0.02 A
由楞次定律可知,回路中的感应电流方向为顺时针,即负方向.
(2)设a、b棒的质量均为m,轻绳拉直后瞬间两棒的共同速度为v,由动量守恒定律得mv0=2mv
b棒在磁场区域Ⅱ中运动产生的动生电动势E2=B2dv
由于a棒带动b棒共同运动并匀速通过磁场区域Ⅱ,故b棒不受安培力,回路中无电流,说明感生电动势与动生电动势相互抵消,即E1=E2
联立解得v=0.5 m/s,v0=1 m/s
(3)由(1)可知,在0~0.1 s内,回路中电流I1=0.02 A,方向为负方向.
b棒通过磁场区域Ⅱ所用的时间t1==0.3 s
因此0.4 s时b棒到达PP1边界,此时B1=0.3 T,故在0.1~0.4 s内,回路中电流I2=0
在0.4~0.5 s内,回路中的感生电动势E3==L1d=0.06 V
回路中电流I3==0.12 A,方向为正方向.
由于b棒未进入磁场区域Ⅰ,t=0.5 s后B1=0,所以在0.5~0.6 s内,回路中电流I4=0
综上所述,0~0.6 s内回路中电流如图所示
7.(1)35 m/s2 方向水平向左 (2)不能 1.2 m (3)m
[解析] (1)P环的初速度为v0=
P环刚弹射入磁场时产生的感应电动势为E0=BLv0
P环中的感应电流为I0=
根据牛顿第二定律可得BI0L=m1a0
联立解得P环刚弹射入磁场时的加速度为a0=35 m/s2
加速度方向水平向左.
(2)P环在磁场中向右运动过程中,由动量定理可得
-BLΔt=m1v-m1v0
其中=,=,ΔΦ=BLx1
联立解得v=9 m/s
P、Q两环发生弹性碰撞,由动量守恒定律可得
m1v=m1v1+m2v2
由机械能守恒定律得
m1v2=m1+m2
联立解得v1=-3 m/s,v2=6 m/s
设P环向左运动的最大距离为x1',根据动量定理可得
-B'LΔt'=0-m1|v1|
其中'=,'=,ΔΦ'=BLx1'
联立解得x1'=1.2 m
由于x1'(3)P、Q两环碰后,Q环向右运动直到与挡板第一次相碰,根据动能定理可得(qE-Ff)x2=Ek2'-m2
第一次碰后动能变为Ek3=(1-k)Ek2'
第一次碰后Q反弹至速度减为零的过程,根据动能定理可得
-(qE+Ff)xQ1=0-Ek3
联立解得xQ1= m
Q环第二次向右运动到与挡板相撞,根据动能定理可得
(qE-Ff)xQ1=Ek3'-0
第二次碰后动能变为Ek4=(1-k)Ek3'
第二次碰后Q反弹至速度减为零的过程,根据动能定理可得
-(qE+Ff)xQ2=0-Ek4
联立解得xQ2= m=xQ1
依次类推,自Q环第一次碰挡板后,每次Q反向运动的位移按等比规律变化,有xQn=xQ1
自Q环第一次碰挡板后到Q环停止运动,Q环运动的总路程x3== m
则Q环在电场中运动的总路程为s=x2+x3= m
1.[2023·湖北卷] 近场通信(NFC)器件应用电磁感应原理进行通讯.其天线类似一个压平的线圈,线圈尺寸从内到外逐渐变大.如图所示,一正方形NFC线圈共3匝,其边长分别为1.0 cm、1.2 cm和1.4 cm.图中线圈外线接入内部芯片时与内部线圈绝缘.若匀强磁场垂直通过此线圈,磁感应强度变化率为103 T/s,则线圈产生的感应电动势最接近( )
A.0.30 V
B.0.44 V
C.0.59 V
D.4.3 V
2.如图所示,在同一个水平面内有彼此绝缘的两个光滑圆环A、B,大圆环A中有顺时针方向的恒定电流I,小圆环B的一半面积在环A内、一半面积在环A外,下列说法正确的是 ( )
A.穿过环B的磁通量为0
B.环B中有持续的感应电流
C.若增大环A内的电流,则环B会向右移动
D.若减小环A内的电流,则环B会产生逆时针方向的感应电流
3.图甲中有一水平向右的匀强磁场,将一个水平放置的金属棒ab以某一水平速度抛出,金属棒在运动过程中始终保持水平,不计空气阻力,金属棒在运动过程中ab两端的电势分别为φa、φb;图乙为法拉第圆盘发电机的原理图,水平匀强磁场垂直于盘面,圆盘绕水平轴C以角速度ω匀速转动,铜片D与圆盘的边缘接触,圆盘、导线和电阻R组成闭合回路,圆盘半径为r,圆盘接入的电阻也为R,其他电阻均可忽略不计,CD两端的电势分别为φC、φD.下列说法正确的是 ( )
A.φa>φb,且a、b两端电势差Uab保持不变
B.φa<φb,且b、a两端电势差Uba逐渐增大
C.φC>φD,且C、D两端电势差UCD=Br2ω
D.φC<φD,通过R的电流大小为
4.如图所示,水平放置的内壁光滑的玻璃圆环半径为R,有一直径略小于圆环内径的带电荷量为q(q>0)的小球在圆环内以速度v0沿顺时针方向匀速转动(俯视).在t=0时刻施加方向竖直向上的变化磁场,磁感应强度B=kt.设运动过程中小球带电荷量不变,不计小球运动产生的磁场及相对论效应.加上磁场后,下列说法正确的是 ( )
A.小球对玻璃圆环的压力不断增大
B.小球对玻璃圆环的压力不断减小
C.小球所受的磁场力一定不断增大
D.小球每运动一周增加的动能为kqπR
5.1831年,法拉第发明了第一台发电机,示意图如图所示.半径为r的铜盘安装在金属轴上,其边缘置于一个磁铁两极之间的狭缝里,铜盘边缘与轴都通过导线和检流计连接.铜盘以周期T匀速旋转,检流计中有电流通过.已知狭缝沿半径方向的长度为a,狭缝间为匀强磁场,磁感应强度为B,忽略狭缝之外的磁场,下列说法正确的是 ( )
A.检流计中电流方向从Q向P
B.若铜盘旋转方向和磁场方向同时反向,则检流计中电流方向也反向
C.铜盘产生的感应电动势为
D.铜盘产生的感应电动势为
6.如图甲所示,水平面上两根足够长的电阻可忽略不计的平行金属导轨间距d=0.2 m,导轨间两个矩形区域Ⅰ和Ⅱ的宽度分别为L1=0.1 m、L2=0.15 m;区域Ⅰ和Ⅱ内有垂直于水平面向上的匀强磁场,磁感应强度大小为B1和B2,其中B1随时间变化的图像如图乙所示,B2=0.1 T.导体棒a和b分别垂直于导轨放置在Ⅰ区域MM1的左侧和Ⅱ区域的右边缘QQ1处,在a、b中点处通过绝缘、松弛的轻绳连接.t=0时,a以平行于导轨的初速度v0向左运动;t=0.1 s时,绳子瞬间拉直带动b共同运动并匀速通过磁场区域Ⅱ.已知a、b质量相等且电阻均为0.25 Ω,仅b与NP、N1P1之间的导轨有摩擦,其余部分摩擦不计,且b未进入Ⅰ区域,g取10 m/s2,回路中电流方向以俯视逆时针为正方向.
(1)求0~0.1 s内回路中的感应电动势大小和感应电流的大小及方向;
(2)求a棒的初速度v0;
(3)通过计算,在图丙中画出0~0.6 s内回路中电流I随时间变化的图像.
7.如图所示,在水平面内有一圆柱形轨道,虚线MN将轨道分为左右两部分,左侧轨道光滑且处于垂直于圆柱外表面的辐向磁场中,右侧粗糙且处于平行于圆柱轴线的匀强电场中.外表面绝缘的导体圆环P套在导轨上位于左端的弹射器内,某时刻弹射器给P一冲量I=14 N·s,将P弹射进入辐向磁场,P向右运动一段时间在边界MN处与绝缘带电圆环Q发生弹性碰撞,碰撞过程中Q带的电荷量不变,碰后P反弹进入磁场,Q则进入右侧电场中,在电场右侧轨道上存在挡板,Q与挡板碰后反弹,碰撞时间极短,碰后损失25%的机械能.已知P、Q两圆环的直径略大于轨道的直径,磁场区域长度为x1=2 m,P、Q两圆环周长均为L=1.0 m,P的质量m1=1 kg,P的电阻R=0.1 Ω,Q的质量m2=2 kg,Q带电荷量q=0.5 C,Q环在虚线MN右侧受到摩擦阻力Ff=6 N,圆环所在位置磁感应强度B=0.5 T,电场强度E=20 N/C,右侧的挡板到MN的距离为x2=3 m.
(1)求P环刚弹射入磁场时的加速度.
(2)P环与Q环碰后能否返回弹射器 若能,请求出返回弹射器时的速度大小;若不能,请求出P环停止时离MN的距离.
(3)求Q环在电场中运动的总路程.
参考答案与详细解析
1.B [解析] 根据法拉第电磁感应定律可知E==S=103×(1.02+1.22+1.42)×10-4 V=0.44 V,故B正确.
2.C [解析] 根据安培定则可知,环A上的电流在其内部产生的磁场均向里,在环B左半圆环内磁场垂直于纸面向里,右半圆环内磁场垂直于纸面向外,因为小圆环B在环A内部的磁场比外部的强,根据磁通量的概念可知,小圆环B在环A内部分的磁通量(向内)大于在环A外部分的磁通量(向外),所以穿过小圆环B的磁通量不为0,且磁通量指向纸面内,故A错误;由于环A中通有恒定电流I,则环B中磁通量不变,无感应电流,故B错误;若增大环A内的电流,则环B内的磁通量向里增加,根据楞次定律,为了阻碍磁通量的增加,环B会向右移动,故C正确;若减小环A内的电流,则环B内的磁通量向里减小,根据楞次定律可判断出,环B会产生顺时针方向的感应电流,故D错误.
3.D [解析] 金属棒ab做平抛运动,竖直方向的分速度与磁感线垂直,根据右手定则可知a点电势高于b点电势,即φa>φb,根据法拉第电磁感应定律得Uab=BLvy=BLgt,即Uab逐渐增大,故A、B错误;圆盘转动过程中,根据右手定则可知D点电势高于C点电势,即φC<φD,由法拉第电磁感应定律可得圆盘产生的感应电动势为E=Br2ω,通过R的电流大小为I==,C、D两端电势差为UCD=-IR=-Br2ω,故C错误,D正确.
4.C [解析] 由楞次定律可判断出,当磁场增强时,会产生顺时针方向的涡旋电场,电场力对小球做正功,使其沿顺时针方向做加速运动,根据牛顿第二定律可知,未加磁场时,圆环对小球的压力FN=m,加磁场后,根据左手定则可知,小球所受的洛伦兹力方向指向圆心,圆环对小球的压力与洛伦兹力的合力提供向心力,由于不确定洛伦兹力与向心力的大小关系,所以小球与圆环之间的弹力变化情况不明,故A、B错误;根据F洛=qvB,由于v与B都增大,所以小球所受的磁场力一定不断增大,故C正确;由动能定理可得W电=ΔEk,小球每运动一周,电场力做功为W电=qU,其中U=·πR2=kπR2,联立解得ΔEk=kπqR2,故D错误.
5.C [解析] 根据右手定则可知,检流计中电流方向从P向Q,若铜盘旋转方向和磁场方向同时反向,则检流计中电流方向不变,故A、B错误;铜盘产生的感应电动势为E=Ba=,故C正确,D错误.
6.(1)0.01 V 0.02 A 负方向
(2)1 m/s (3)如图所示
[解析] (1)由图乙可知,0~0.1 s内,=0.5 T/s
则回路中的感生电动势E1==L1d=0.01 V
回路中的感应电流I1==0.02 A
由楞次定律可知,回路中的感应电流方向为顺时针,即负方向.
(2)设a、b棒的质量均为m,轻绳拉直后瞬间两棒的共同速度为v,由动量守恒定律得mv0=2mv
b棒在磁场区域Ⅱ中运动产生的动生电动势E2=B2dv
由于a棒带动b棒共同运动并匀速通过磁场区域Ⅱ,故b棒不受安培力,回路中无电流,说明感生电动势与动生电动势相互抵消,即E1=E2
联立解得v=0.5 m/s,v0=1 m/s
(3)由(1)可知,在0~0.1 s内,回路中电流I1=0.02 A,方向为负方向.
b棒通过磁场区域Ⅱ所用的时间t1==0.3 s
因此0.4 s时b棒到达PP1边界,此时B1=0.3 T,故在0.1~0.4 s内,回路中电流I2=0
在0.4~0.5 s内,回路中的感生电动势E3==L1d=0.06 V
回路中电流I3==0.12 A,方向为正方向.
由于b棒未进入磁场区域Ⅰ,t=0.5 s后B1=0,所以在0.5~0.6 s内,回路中电流I4=0
综上所述,0~0.6 s内回路中电流如图所示
7.(1)35 m/s2 方向水平向左 (2)不能 1.2 m (3)m
[解析] (1)P环的初速度为v0=
P环刚弹射入磁场时产生的感应电动势为E0=BLv0
P环中的感应电流为I0=
根据牛顿第二定律可得BI0L=m1a0
联立解得P环刚弹射入磁场时的加速度为a0=35 m/s2
加速度方向水平向左.
(2)P环在磁场中向右运动过程中,由动量定理可得
-BLΔt=m1v-m1v0
其中=,=,ΔΦ=BLx1
联立解得v=9 m/s
P、Q两环发生弹性碰撞,由动量守恒定律可得
m1v=m1v1+m2v2
由机械能守恒定律得
m1v2=m1+m2
联立解得v1=-3 m/s,v2=6 m/s
设P环向左运动的最大距离为x1',根据动量定理可得
-B'LΔt'=0-m1|v1|
其中'=,'=,ΔΦ'=BLx1'
联立解得x1'=1.2 m
由于x1'
第一次碰后动能变为Ek3=(1-k)Ek2'
第一次碰后Q反弹至速度减为零的过程,根据动能定理可得
-(qE+Ff)xQ1=0-Ek3
联立解得xQ1= m
Q环第二次向右运动到与挡板相撞,根据动能定理可得
(qE-Ff)xQ1=Ek3'-0
第二次碰后动能变为Ek4=(1-k)Ek3'
第二次碰后Q反弹至速度减为零的过程,根据动能定理可得
-(qE+Ff)xQ2=0-Ek4
联立解得xQ2= m=xQ1
依次类推,自Q环第一次碰挡板后,每次Q反向运动的位移按等比规律变化,有xQn=xQ1
自Q环第一次碰挡板后到Q环停止运动,Q环运动的总路程x3== m
则Q环在电场中运动的总路程为s=x2+x3= m
同课章节目录
