2025届高考物理二轮复习:微专题9 电磁感应实践性应用专题-专项训练 (含解析)
文档属性
| 名称 | 2025届高考物理二轮复习:微专题9 电磁感应实践性应用专题-专项训练 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 194.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-05 13:29:12 | ||
图片预览


文档简介
2025届高考物理二轮复习
微专题9 电磁感应实践性应用专题-专项训练
1.[2024·丽水模拟] 电和磁有许多相似之处,比如同种电荷相斥,同名磁极也相斥,异种电荷相吸,异名磁极也相吸;变化的电场激发磁场,变化的磁场也能激发电场.著名的英国物理学家狄拉克曾预言磁单极子可以像正负电荷一样独立存在,所谓磁单极子是指仅带有N极或S极单一磁极的磁性物质,它们的磁感线分布类似于点电荷的电场线分布(如图甲所示).若存在一N极磁单极子如图乙所示,固定于水平桌面上,其上覆盖一半径为r的半球壳,球心恰好在磁单极子处,球壳表面绝缘光滑.现在半球壳上方轻轻放置一特殊材料制成的质量为m的弹性导电线圈,线圈开始时处于原长,半径为r0=r,电阻为R,线圈在重力作用下沿着半球壳下滑,下滑过程中线圈平面始终在水平面内,当线圈下滑高度h=0.2r时速度为v.已知与磁单极子距离为d处的磁感应强度大小为B=,弹性线圈存储的势能与橡皮筋类似,当线圈长度伸长Δx时存储的弹性势能为Ep=k'(Δx)2,上述式中k、k'均为常数,重力加速度为g,求:
(1)半球壳上各处磁感应强度大小和穿过半球壳的磁通量(球体表面积计算公式:S=4πr2);
(2)线圈下落高度h=0.2r时产生的感应电流大小和方向(从上往下看);
(3)线圈下落高度h=0.2r的过程中产生的焦耳热Q.
2.[2024·杭州二中模拟] 如图甲所示是一种可测速的跑步机,它的测速原理如图乙所示.该机上底面固定有间距为L、宽度为d的平行金属电极,电极间充满磁感应强度为B、方向垂直于纸面向里的匀强磁场,电极通过导线与电压表和阻值为R的定值电阻相连接.绝缘橡胶带上每隔距离 d就嵌入一个电阻为r的平行细金属条,跑步过程中,绝缘橡胶带跟随脚步一起运动,金属条和电极之间接触良好且任意时刻仅有一根金属条处于磁场中.现在测出t时间内电压表读数恒为 U,设人与跑步机间无相对滑动,电压表内阻很大(视为理想电表).
(1)判断流过定值电阻R的电流方向;
(2)求橡胶带运动速度的大小;
(3)若跑步过程中,人体消耗的能量有20%用于克服磁场力做功,求t时间内人体消耗的能量.
3.如图甲所示为高温超导磁悬浮列车,这是一种高速低耗的新型交通工具,它的驱动系统可简化为如图乙所示的模型.固定在列车下端的动力绕组视为一个矩形纯电阻金属框,电阻为R,金属框置于xOy平面内,长为L的MN边平行于y轴,宽为d的NP边平行于x轴.列车轨道沿Ox方向,轨道区域内存在垂直于金属框平面的磁场,磁感应强度B沿y轴方向大小相同,沿Ox方向按正弦规律分布,其空间间隔为λ,最大值为B0,如图丙所示.整个磁场以速度v0沿Ox方向匀速平移,使列车获得沿Ox方向的驱动力.为使驱动效果最佳,λ与d之间需满足特定关系.
(1)求λ与d之间满足的关系式;
(2)某时刻列车速度为v1,求列车可能受到的最大驱动力;
(3)实际上的驱动力是周期性变化的,但只要λ足够小,我们感受不到这种变化.若列车受到的阻力与速度的大小成正比,比例系数为k,则列车的最终速度v2为多大 此时驱动力大小的实际变化周期为多少 (以下供类比参考:让交变电流和直流电通过同样的电阻,如果它们在相同时间内产生的热量相等,我们就把直流电的值叫作交变电流的有效值.若通过电阻R的正弦交变电流的瞬时值为i=Imsin ωt,可证明其有效值与最大值的关系为I=,在时间t内的焦耳热为Q=I2Rt)
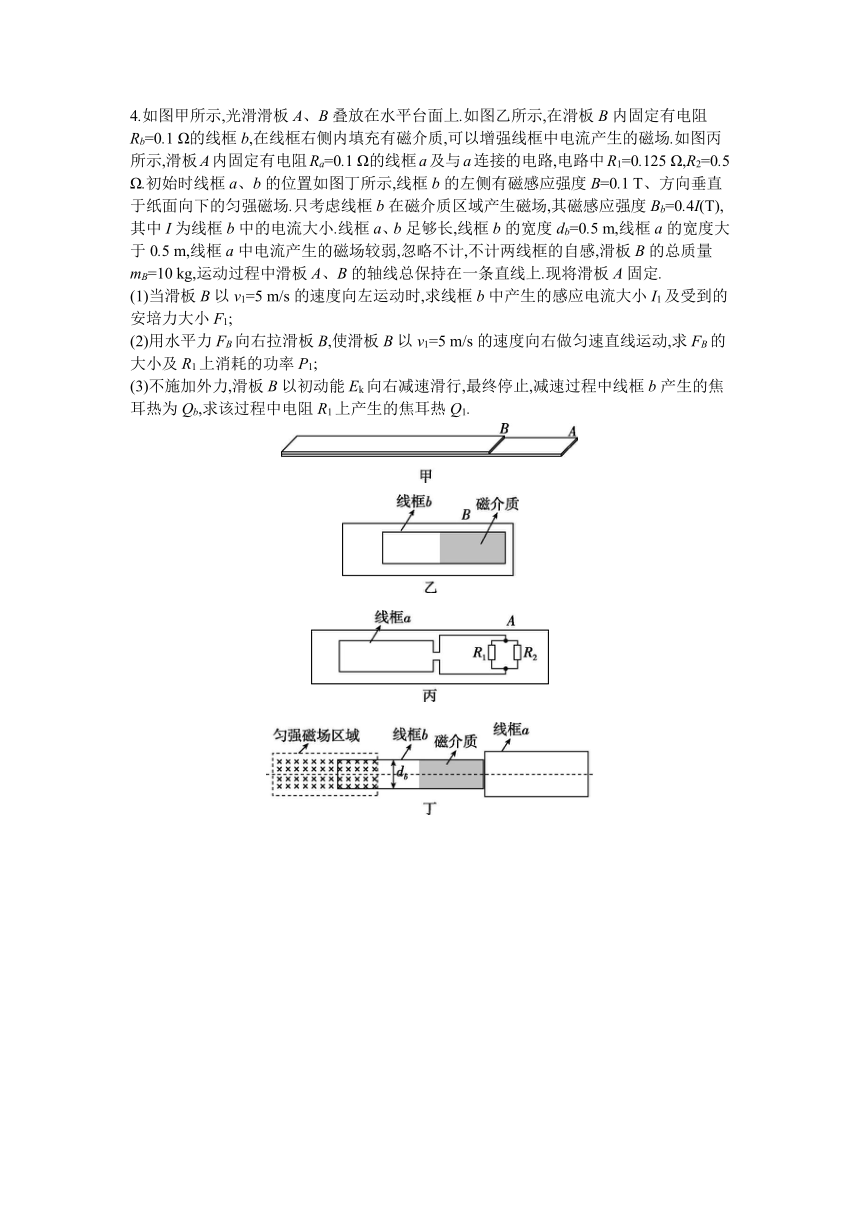
4.如图甲所示,光滑滑板A、B叠放在水平台面上.如图乙所示,在滑板B内固定有电阻Rb=0.1 Ω的线框b,在线框右侧内填充有磁介质,可以增强线框中电流产生的磁场.如图丙所示,滑板A内固定有电阻Ra=0.1 Ω的线框a及与a连接的电路,电路中R1=0.125 Ω,R2=0.5 Ω.初始时线框a、b的位置如图丁所示,线框b的左侧有磁感应强度B=0.1 T、方向垂直于纸面向下的匀强磁场.只考虑线框b在磁介质区域产生磁场,其磁感应强度Bb=0.4I(T),其中I为线框b中的电流大小.线框a、b足够长,线框b的宽度db=0.5 m,线框a的宽度大于0.5 m,线框a中电流产生的磁场较弱,忽略不计,不计两线框的自感,滑板B的总质量mB=10 kg,运动过程中滑板A、B的轴线总保持在一条直线上.现将滑板A固定.
(1)当滑板B以v1=5 m/s的速度向左运动时,求线框b中产生的感应电流大小I1及受到的安培力大小F1;
(2)用水平力FB向右拉滑板B,使滑板B以v1=5 m/s的速度向右做匀速直线运动,求FB的大小及R1上消耗的功率P1;
(3)不施加外力,滑板B以初动能Ek向右减速滑行,最终停止,减速过程中线框b产生的焦耳热为Qb,求该过程中电阻R1上产生的焦耳热Q1.
参考答案与详细解析
1.(1) 2kπr (2) 顺时针方向 (3)mgr-mv2-
[解析] (1)半球壳面上磁感应强度大小相同,都为B=
穿过半球面的磁通量等于磁感应强度与半球壳表面积的乘积,即Φ=2Bπr2=2kπr
(2)根据楞次定律可知,线圈下落过程中产生的感应电流方向为俯视顺时针方向.
由几何关系可知,线圈开始时高度h0==r
当线圈下落高度h=0.2R时,由几何关系可知,线圈半径变为r1==r
此时可等效成长度为l=2πr1的导线在切割磁感线,产生的感应电动势E=Blv=
此时线圈导线长度与开始时长度之比==,则此时导线横截面积与开始时横截面积之比==,由电阻定律R=ρ,可知此时电阻变为R1=·R=R
则线圈中产生的感应电流大小为I==
(3)线圈下落过程中,由能量守恒定律得
mgh=mv2+Q+k'(Δx)2
其中Δx=2πr1-2πr0=πr
解得Q=mgr-mv2-
2.(1)从a到b (2)U (3)
[解析] (1)根据右手定则可知,流过定值电阻R的电流方向是从a到b.
(2)根据法拉第电磁感应定律有E=BLv
回路中电流大小为I=
电压表的示数U=IR
联立解得v=U
(3)金属条所受的安培力大小FA=BIL
t时间内金属条克服安培力做的功W=FAvt
t时间内人体消耗的能量E人=
联立解得E人=
3.(1)λ=(k=0,1,2,…) (2)
(3)
[解析] (1)MN、PQ应位于磁场中磁感应强度同为最大值B0且反向的地方,这会使金属框中的感应电流最强,受到的安培力最大.因此d应为的奇数倍,即d=,也就是λ=(k=0,1,2,…)
(2)金属框中的感应电动势最大值为Em=2B0L
根据闭合电路欧姆定律得Im==
列车受到的最大驱动力Fm=2B0ImL=
(3)MN、PQ位于磁场中的磁感应强度总是大小相同、方向相反的,周期性变化的,可以写成Bt=B0sin ωt=B0sin t
其中T=
(λ越小则越感受不到驱动力变化)
列车受到的驱动力Ft=2BtIL=sin 2 ωt
一个周期内驱动力的冲量与阻力的冲量大小相等,方向相反,即FtΔt=FfΔt
其中Δt=T
与正弦式交流电的最大值和有效值进行类比,驱动力随时间变化的“有效值”等于阻力的大小,即=kv2
解得v2=
驱动力大小的实际变化周期T'===
4.(1)2.5 A 0.125 N (2)6.375 N 12.5 W (3)(Ek-Qb)
[解析] (1)与滑板B以v1=5 m/s的速度向左运动时,线框b中产生的感应电动势E1=Bdbv1=0.25 V
感应电流大小I1==2.5 A
受到的安培力大小F1=BI1db=0.125 N
(2)用水平力FB向右拉滑板B,使滑板B以v1=5 m/s的速度向右做匀速直线运动,则线圈b中的电流仍为I1=2.5 A,此时线框b在磁介质区域产生的磁场的磁感应强度
Bb=0.4I1(T)=1 T
此时线圈a中产生的感应电动势E2=Bbdbv1=2.5 V
R1和R2并联后的电阻R==0.1 Ω
线圈a中产生的感应电流I2==12.5 A
水平力FB=BI1db+BbI2db=6.375 N
R1上的电压U1=I2R=1.25 V
R1上消耗的功率P1==12.5 W
(3)不施加外力,滑板B以初动能Ek向右减速滑行,最终停止,则两线圈产生的焦耳热之和为Ek,由于减速过程中线框b产生的焦耳热为Qb,则线框a产生的焦耳热为Qa=Ek-Qb
因R1、R2两电阻并联的电阻R=Ra,故R1、R2两电阻产生的焦耳热之和为Qa,而该过程中电阻R1和R2产生的焦耳热之比为,所以电阻R1上产生的焦耳热Q1=Qa×=(Ek-Qb)
微专题9 电磁感应实践性应用专题-专项训练
1.[2024·丽水模拟] 电和磁有许多相似之处,比如同种电荷相斥,同名磁极也相斥,异种电荷相吸,异名磁极也相吸;变化的电场激发磁场,变化的磁场也能激发电场.著名的英国物理学家狄拉克曾预言磁单极子可以像正负电荷一样独立存在,所谓磁单极子是指仅带有N极或S极单一磁极的磁性物质,它们的磁感线分布类似于点电荷的电场线分布(如图甲所示).若存在一N极磁单极子如图乙所示,固定于水平桌面上,其上覆盖一半径为r的半球壳,球心恰好在磁单极子处,球壳表面绝缘光滑.现在半球壳上方轻轻放置一特殊材料制成的质量为m的弹性导电线圈,线圈开始时处于原长,半径为r0=r,电阻为R,线圈在重力作用下沿着半球壳下滑,下滑过程中线圈平面始终在水平面内,当线圈下滑高度h=0.2r时速度为v.已知与磁单极子距离为d处的磁感应强度大小为B=,弹性线圈存储的势能与橡皮筋类似,当线圈长度伸长Δx时存储的弹性势能为Ep=k'(Δx)2,上述式中k、k'均为常数,重力加速度为g,求:
(1)半球壳上各处磁感应强度大小和穿过半球壳的磁通量(球体表面积计算公式:S=4πr2);
(2)线圈下落高度h=0.2r时产生的感应电流大小和方向(从上往下看);
(3)线圈下落高度h=0.2r的过程中产生的焦耳热Q.
2.[2024·杭州二中模拟] 如图甲所示是一种可测速的跑步机,它的测速原理如图乙所示.该机上底面固定有间距为L、宽度为d的平行金属电极,电极间充满磁感应强度为B、方向垂直于纸面向里的匀强磁场,电极通过导线与电压表和阻值为R的定值电阻相连接.绝缘橡胶带上每隔距离 d就嵌入一个电阻为r的平行细金属条,跑步过程中,绝缘橡胶带跟随脚步一起运动,金属条和电极之间接触良好且任意时刻仅有一根金属条处于磁场中.现在测出t时间内电压表读数恒为 U,设人与跑步机间无相对滑动,电压表内阻很大(视为理想电表).
(1)判断流过定值电阻R的电流方向;
(2)求橡胶带运动速度的大小;
(3)若跑步过程中,人体消耗的能量有20%用于克服磁场力做功,求t时间内人体消耗的能量.
3.如图甲所示为高温超导磁悬浮列车,这是一种高速低耗的新型交通工具,它的驱动系统可简化为如图乙所示的模型.固定在列车下端的动力绕组视为一个矩形纯电阻金属框,电阻为R,金属框置于xOy平面内,长为L的MN边平行于y轴,宽为d的NP边平行于x轴.列车轨道沿Ox方向,轨道区域内存在垂直于金属框平面的磁场,磁感应强度B沿y轴方向大小相同,沿Ox方向按正弦规律分布,其空间间隔为λ,最大值为B0,如图丙所示.整个磁场以速度v0沿Ox方向匀速平移,使列车获得沿Ox方向的驱动力.为使驱动效果最佳,λ与d之间需满足特定关系.
(1)求λ与d之间满足的关系式;
(2)某时刻列车速度为v1,求列车可能受到的最大驱动力;
(3)实际上的驱动力是周期性变化的,但只要λ足够小,我们感受不到这种变化.若列车受到的阻力与速度的大小成正比,比例系数为k,则列车的最终速度v2为多大 此时驱动力大小的实际变化周期为多少 (以下供类比参考:让交变电流和直流电通过同样的电阻,如果它们在相同时间内产生的热量相等,我们就把直流电的值叫作交变电流的有效值.若通过电阻R的正弦交变电流的瞬时值为i=Imsin ωt,可证明其有效值与最大值的关系为I=,在时间t内的焦耳热为Q=I2Rt)
4.如图甲所示,光滑滑板A、B叠放在水平台面上.如图乙所示,在滑板B内固定有电阻Rb=0.1 Ω的线框b,在线框右侧内填充有磁介质,可以增强线框中电流产生的磁场.如图丙所示,滑板A内固定有电阻Ra=0.1 Ω的线框a及与a连接的电路,电路中R1=0.125 Ω,R2=0.5 Ω.初始时线框a、b的位置如图丁所示,线框b的左侧有磁感应强度B=0.1 T、方向垂直于纸面向下的匀强磁场.只考虑线框b在磁介质区域产生磁场,其磁感应强度Bb=0.4I(T),其中I为线框b中的电流大小.线框a、b足够长,线框b的宽度db=0.5 m,线框a的宽度大于0.5 m,线框a中电流产生的磁场较弱,忽略不计,不计两线框的自感,滑板B的总质量mB=10 kg,运动过程中滑板A、B的轴线总保持在一条直线上.现将滑板A固定.
(1)当滑板B以v1=5 m/s的速度向左运动时,求线框b中产生的感应电流大小I1及受到的安培力大小F1;
(2)用水平力FB向右拉滑板B,使滑板B以v1=5 m/s的速度向右做匀速直线运动,求FB的大小及R1上消耗的功率P1;
(3)不施加外力,滑板B以初动能Ek向右减速滑行,最终停止,减速过程中线框b产生的焦耳热为Qb,求该过程中电阻R1上产生的焦耳热Q1.
参考答案与详细解析
1.(1) 2kπr (2) 顺时针方向 (3)mgr-mv2-
[解析] (1)半球壳面上磁感应强度大小相同,都为B=
穿过半球面的磁通量等于磁感应强度与半球壳表面积的乘积,即Φ=2Bπr2=2kπr
(2)根据楞次定律可知,线圈下落过程中产生的感应电流方向为俯视顺时针方向.
由几何关系可知,线圈开始时高度h0==r
当线圈下落高度h=0.2R时,由几何关系可知,线圈半径变为r1==r
此时可等效成长度为l=2πr1的导线在切割磁感线,产生的感应电动势E=Blv=
此时线圈导线长度与开始时长度之比==,则此时导线横截面积与开始时横截面积之比==,由电阻定律R=ρ,可知此时电阻变为R1=·R=R
则线圈中产生的感应电流大小为I==
(3)线圈下落过程中,由能量守恒定律得
mgh=mv2+Q+k'(Δx)2
其中Δx=2πr1-2πr0=πr
解得Q=mgr-mv2-
2.(1)从a到b (2)U (3)
[解析] (1)根据右手定则可知,流过定值电阻R的电流方向是从a到b.
(2)根据法拉第电磁感应定律有E=BLv
回路中电流大小为I=
电压表的示数U=IR
联立解得v=U
(3)金属条所受的安培力大小FA=BIL
t时间内金属条克服安培力做的功W=FAvt
t时间内人体消耗的能量E人=
联立解得E人=
3.(1)λ=(k=0,1,2,…) (2)
(3)
[解析] (1)MN、PQ应位于磁场中磁感应强度同为最大值B0且反向的地方,这会使金属框中的感应电流最强,受到的安培力最大.因此d应为的奇数倍,即d=,也就是λ=(k=0,1,2,…)
(2)金属框中的感应电动势最大值为Em=2B0L
根据闭合电路欧姆定律得Im==
列车受到的最大驱动力Fm=2B0ImL=
(3)MN、PQ位于磁场中的磁感应强度总是大小相同、方向相反的,周期性变化的,可以写成Bt=B0sin ωt=B0sin t
其中T=
(λ越小则越感受不到驱动力变化)
列车受到的驱动力Ft=2BtIL=sin 2 ωt
一个周期内驱动力的冲量与阻力的冲量大小相等,方向相反,即FtΔt=FfΔt
其中Δt=T
与正弦式交流电的最大值和有效值进行类比,驱动力随时间变化的“有效值”等于阻力的大小,即=kv2
解得v2=
驱动力大小的实际变化周期T'===
4.(1)2.5 A 0.125 N (2)6.375 N 12.5 W (3)(Ek-Qb)
[解析] (1)与滑板B以v1=5 m/s的速度向左运动时,线框b中产生的感应电动势E1=Bdbv1=0.25 V
感应电流大小I1==2.5 A
受到的安培力大小F1=BI1db=0.125 N
(2)用水平力FB向右拉滑板B,使滑板B以v1=5 m/s的速度向右做匀速直线运动,则线圈b中的电流仍为I1=2.5 A,此时线框b在磁介质区域产生的磁场的磁感应强度
Bb=0.4I1(T)=1 T
此时线圈a中产生的感应电动势E2=Bbdbv1=2.5 V
R1和R2并联后的电阻R==0.1 Ω
线圈a中产生的感应电流I2==12.5 A
水平力FB=BI1db+BbI2db=6.375 N
R1上的电压U1=I2R=1.25 V
R1上消耗的功率P1==12.5 W
(3)不施加外力,滑板B以初动能Ek向右减速滑行,最终停止,则两线圈产生的焦耳热之和为Ek,由于减速过程中线框b产生的焦耳热为Qb,则线框a产生的焦耳热为Qa=Ek-Qb
因R1、R2两电阻并联的电阻R=Ra,故R1、R2两电阻产生的焦耳热之和为Qa,而该过程中电阻R1和R2产生的焦耳热之比为,所以电阻R1上产生的焦耳热Q1=Qa×=(Ek-Qb)
同课章节目录
