2025届高考物理二轮复习:微专题10 热学计算题型突破-专项训练(含解析)
文档属性
| 名称 | 2025届高考物理二轮复习:微专题10 热学计算题型突破-专项训练(含解析) | 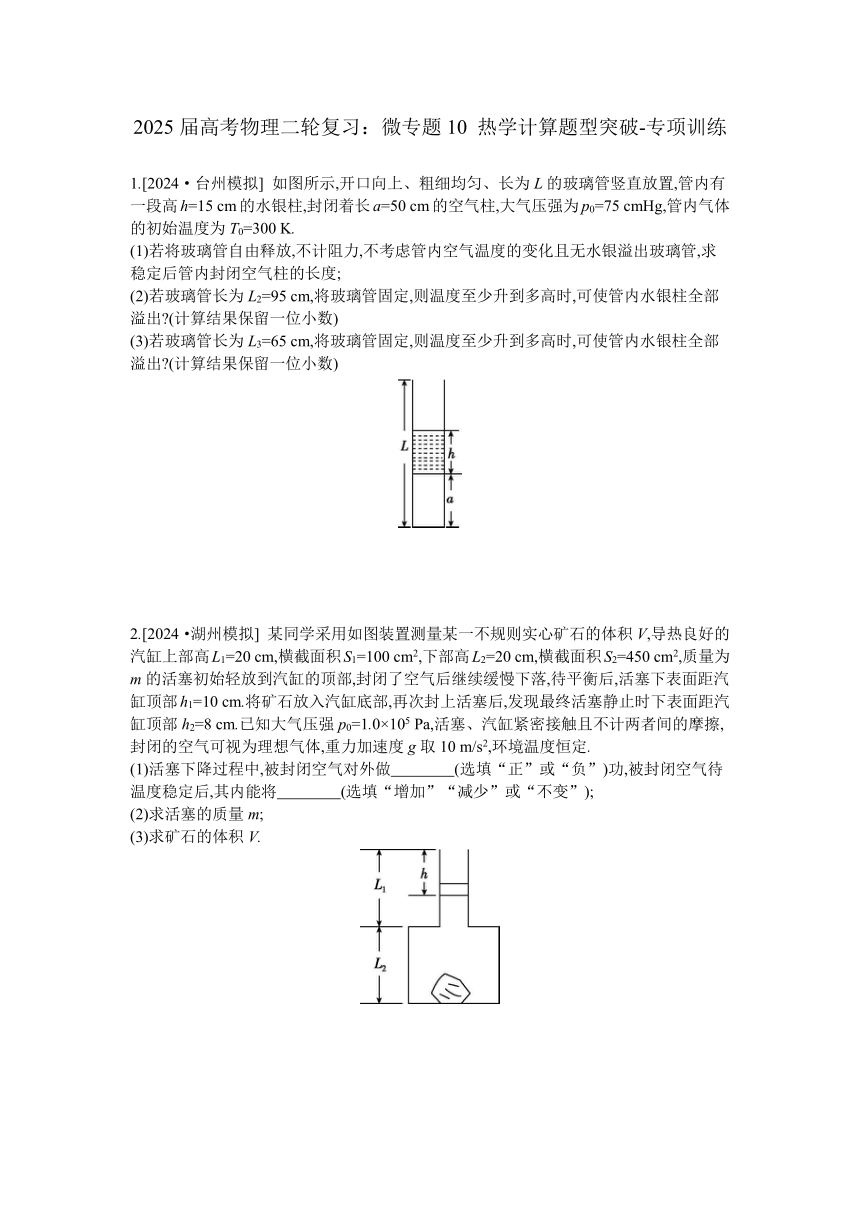 | |
| 格式 | docx | ||
| 文件大小 | 81.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-05 13:30:25 | ||
图片预览


文档简介
2025届高考物理二轮复习:微专题10 热学计算题型突破-专项训练
1.[2024·台州模拟] 如图所示,开口向上、粗细均匀、长为L的玻璃管竖直放置,管内有一段高h=15 cm的水银柱,封闭着长a=50 cm的空气柱,大气压强为p0=75 cmHg,管内气体的初始温度为T0=300 K.
(1)若将玻璃管自由释放,不计阻力,不考虑管内空气温度的变化且无水银溢出玻璃管,求稳定后管内封闭空气柱的长度;
(2)若玻璃管长为L2=95 cm,将玻璃管固定,则温度至少升到多高时,可使管内水银柱全部溢出 (计算结果保留一位小数)
(3)若玻璃管长为L3=65 cm,将玻璃管固定,则温度至少升到多高时,可使管内水银柱全部溢出 (计算结果保留一位小数)
2.[2024·湖州模拟] 某同学采用如图装置测量某一不规则实心矿石的体积V,导热良好的汽缸上部高L1=20 cm,横截面积S1=100 cm2,下部高L2=20 cm,横截面积S2=450 cm2,质量为m的活塞初始轻放到汽缸的顶部,封闭了空气后继续缓慢下落,待平衡后,活塞下表面距汽缸顶部h1=10 cm.将矿石放入汽缸底部,再次封上活塞后,发现最终活塞静止时下表面距汽缸顶部h2=8 cm.已知大气压强p0=1.0×105 Pa,活塞、汽缸紧密接触且不计两者间的摩擦,封闭的空气可视为理想气体,重力加速度g取10 m/s2,环境温度恒定.
(1)活塞下降过程中,被封闭空气对外做 (选填“正”或“负”)功,被封闭空气待温度稳定后,其内能将 (选填“增加”“减少”或“不变”);
(2)求活塞的质量m;
(3)求矿石的体积V.
3.[2024·温州模拟] 如图所示装置是一个高为H、底面积为S的圆柱形导热汽缸的截面图.汽缸顶部安装有挡柱,底部通过阀门(大小不计)连接一个充气源,厚度不计的活塞封闭有一部分空气,活塞距离汽缸底部高度h=H,质量M=(g为重力加速度),活塞与汽缸之间的摩擦可忽略.大气压强为p0,空气可视为理想气体.现用充气源给汽缸充气,每次可往容器中充入压强为p0、体积为SH的空气,充气过程温度保持不变.求:
(1)初始时封闭气体的压强大小;
(2)第一次充气前后,活塞缓慢上升的高度;
(3)充气45次之后,缸内气体的压强大小.
4.[2024·广东佛山模拟] 一个容积为V0=9.9 L的导热汽缸下接一圆柱形管,二者总质量为M=900 g,现用质量m=100 g、横截面积S=10 cm2、厚度可忽略不计的活塞封闭一定质量的理想气体,活塞与圆管管壁间摩擦不计.活塞下端连接弹簧,弹簧下端与地面固定,汽缸始终保持竖直.开始时气体温度为T1=297 K,活塞处在A位置,汽缸内气体压强为p1.随着环境温度缓慢升高到T2,活塞恰能缓慢移至容器底部B位置处,已知A、B间距离h=10 cm,外界大气压强p0=1.01×105 Pa,g取10 m/s2.
(1)环境温度由T1缓慢升高到T2过程中,汽缸内气体压强 (选填“变化”或“不变”);
(2)求汽缸内的气体压强p1及环境温度T2;
(3)升温过程中,若气体内能增加了ΔU=25 J,求气体需要从外界吸收的热量.
5.[2024·金华模拟] 如图所示,倾角θ=30°的光滑斜面固定在水平地面上,有一长L=16 cm的绝热汽缸与绝热活塞静置于斜面上,活塞与重物通过不可伸长的轻绳连接,此时重物对地面恰好无压力,轻绳OA段与斜面平行,活塞距离汽缸底部.活塞质量m=1 kg,重物质量M=2 kg,活塞面积S=10 cm2,大气压p0=1.0×105 Pa,缸内封闭的理想气体温度T0=300 K,缸内气体分子总动能满足Ek=kT,其中k=0.8 J/K,g取10 m/s2.活塞厚度及活塞与汽缸壁的摩擦忽略不计,活塞始终与汽缸壁垂直且不漏气.当电热丝通电加热时,活塞缓慢到达汽缸口.
(1)加热过程气体压强 (选填“增大”“减小”或“不变”),汽缸内壁单位面积单位时间内受到分子的撞击数 (选填“增大”“减小”或“不变”);
(2)求加热前汽缸内气体的压强p1;
(3)求加热过程汽缸内气体吸收的热量Q.
参考答案与详细解析
1.(1)60 cm (2)481.7 K (3)325 K
[解析] (1)若将玻璃管自由释放,不计阻力,则整体做自由落体运动,封闭气体的压强为p0=75 cmHg,根据玻意耳定律有p1Sa=p0Sa'
又p1=p0+ρgh=90 cmHg
解得稳定后管内封闭空气柱的长度为a'=60 cm
(2)温度升高,封闭气体压强不变,体积增大,水银柱升高,当水银柱上升至管口时,温度继续升高,水银开始逸出,气体压强减小.设温度为T1时,管内剩余水银柱高度为h',此时不用再升高温度,水银可自动从管中溢出,根据理想气体状态方程有=
可以使水银全部溢出时T1最大,则应最大,代入数据得h'=10 cm
解得T1≈481.7 K
故温度至少升到481.7 K时,可使管内水银柱全部溢出.
(3)若玻璃管长为L3=65 cm,同理,设管内剩内水银柱为h″时处于临界状态,水银自动溢出,根据理想气体状态方程有
=
代入数据解得h″=-5,而h″≥0,故h″取0
解得T2≈325 K
故温度至少升到325 K时,可使管内水银柱全部溢出.
2.(1)负 不变 (2)10 kg (3)2200 cm3
[解析] (1)活塞下降过程中,气体体积减小,被封闭空气对外做负功,被封闭空气待温度稳定后,由于汽缸导热良好,温度不变,封闭的空气可视为理想气体,其内能将不变.
(2)对活塞进行分析有
mg+p0S1=p1S1
汽缸导热良好,温度不变,即气体发生的是等温变化,根据玻意耳定律有
p0=p1[(L1-h1)S1+L2S2]
解得m=10 kg.
(3)再次平衡时,根据玻意耳定律有
p0=p1[(L1-h2)S1+L2S2-V]
解得V=2200 cm3.
3.(1)p0 (2)H (3)2p0
[解析] (1)对活塞受力分析,由平衡条件得
p0S+Mg=p1S
解得p1=p0
(2)第一次充气时,对充进部分的气体研究,有
p0=p1
解得h1=H
(3)活塞与汽缸挡柱刚好接触时,有
n==30次
则充气的前30次气体做等压变化,后15次压强变化,有
p1S=p2HS
解得p2=2p0
4.(1)不变 (2)1.1×105 Pa 300 K (3)36 J
[解析] (1)对汽缸受力分析,变化前有Mg+p0S=p1S,变化后有Mg+p0S=p1'S,可知p1=p1',则可知,环境温度由T1缓慢升高到T2过程中,汽缸内气体压强不变.
(2)以汽缸为研究对象,根据平衡条件可知
Mg+p0S=p1S
解得p1=1.1×105 Pa
气体升温膨胀过程为等压过程,由盖-吕萨克定律有
=
解得T2=300 K.
(3)由热力学第一定律可知ΔU=W+Q
气体膨胀对外做功,则可得
W=-p1Sh=-11 J
所以气体需要从外界吸收热量Q=36 J.
5.(1)不变 减小 (2)8.5×104 Pa (3)83.4 J
[解析] (1)加热过程,活塞、汽缸和重物整体受力不变,汽缸向下滑动,活塞的受力不变,即气体对活塞的压力不变,气体的压强不变;加热过程,气体的温度升高,气体的平均动能增大,气体分子对汽缸内壁的平均作用力变大,但是气体的压强不变,即单位面积单位时间内气体分子的作用力不变,则汽缸内壁单位面积单位时间内受到分子的撞击数减小.
(2)活塞受力平衡,有
FT+p1S=mgsin θ+p0S
重物受力平衡,有FT=Mg
可得气体压强p1=p0+=8.5×104 Pa.
(3)加热过程为等压变化,满足=
得T1=400 K
气体内能变化ΔU=ΔEk=80 J
气体对外做功W=-p1S=-3.4 J
根据热力学第一定律ΔU=W+Q
可得Q=83.4 J.
1.[2024·台州模拟] 如图所示,开口向上、粗细均匀、长为L的玻璃管竖直放置,管内有一段高h=15 cm的水银柱,封闭着长a=50 cm的空气柱,大气压强为p0=75 cmHg,管内气体的初始温度为T0=300 K.
(1)若将玻璃管自由释放,不计阻力,不考虑管内空气温度的变化且无水银溢出玻璃管,求稳定后管内封闭空气柱的长度;
(2)若玻璃管长为L2=95 cm,将玻璃管固定,则温度至少升到多高时,可使管内水银柱全部溢出 (计算结果保留一位小数)
(3)若玻璃管长为L3=65 cm,将玻璃管固定,则温度至少升到多高时,可使管内水银柱全部溢出 (计算结果保留一位小数)
2.[2024·湖州模拟] 某同学采用如图装置测量某一不规则实心矿石的体积V,导热良好的汽缸上部高L1=20 cm,横截面积S1=100 cm2,下部高L2=20 cm,横截面积S2=450 cm2,质量为m的活塞初始轻放到汽缸的顶部,封闭了空气后继续缓慢下落,待平衡后,活塞下表面距汽缸顶部h1=10 cm.将矿石放入汽缸底部,再次封上活塞后,发现最终活塞静止时下表面距汽缸顶部h2=8 cm.已知大气压强p0=1.0×105 Pa,活塞、汽缸紧密接触且不计两者间的摩擦,封闭的空气可视为理想气体,重力加速度g取10 m/s2,环境温度恒定.
(1)活塞下降过程中,被封闭空气对外做 (选填“正”或“负”)功,被封闭空气待温度稳定后,其内能将 (选填“增加”“减少”或“不变”);
(2)求活塞的质量m;
(3)求矿石的体积V.
3.[2024·温州模拟] 如图所示装置是一个高为H、底面积为S的圆柱形导热汽缸的截面图.汽缸顶部安装有挡柱,底部通过阀门(大小不计)连接一个充气源,厚度不计的活塞封闭有一部分空气,活塞距离汽缸底部高度h=H,质量M=(g为重力加速度),活塞与汽缸之间的摩擦可忽略.大气压强为p0,空气可视为理想气体.现用充气源给汽缸充气,每次可往容器中充入压强为p0、体积为SH的空气,充气过程温度保持不变.求:
(1)初始时封闭气体的压强大小;
(2)第一次充气前后,活塞缓慢上升的高度;
(3)充气45次之后,缸内气体的压强大小.
4.[2024·广东佛山模拟] 一个容积为V0=9.9 L的导热汽缸下接一圆柱形管,二者总质量为M=900 g,现用质量m=100 g、横截面积S=10 cm2、厚度可忽略不计的活塞封闭一定质量的理想气体,活塞与圆管管壁间摩擦不计.活塞下端连接弹簧,弹簧下端与地面固定,汽缸始终保持竖直.开始时气体温度为T1=297 K,活塞处在A位置,汽缸内气体压强为p1.随着环境温度缓慢升高到T2,活塞恰能缓慢移至容器底部B位置处,已知A、B间距离h=10 cm,外界大气压强p0=1.01×105 Pa,g取10 m/s2.
(1)环境温度由T1缓慢升高到T2过程中,汽缸内气体压强 (选填“变化”或“不变”);
(2)求汽缸内的气体压强p1及环境温度T2;
(3)升温过程中,若气体内能增加了ΔU=25 J,求气体需要从外界吸收的热量.
5.[2024·金华模拟] 如图所示,倾角θ=30°的光滑斜面固定在水平地面上,有一长L=16 cm的绝热汽缸与绝热活塞静置于斜面上,活塞与重物通过不可伸长的轻绳连接,此时重物对地面恰好无压力,轻绳OA段与斜面平行,活塞距离汽缸底部.活塞质量m=1 kg,重物质量M=2 kg,活塞面积S=10 cm2,大气压p0=1.0×105 Pa,缸内封闭的理想气体温度T0=300 K,缸内气体分子总动能满足Ek=kT,其中k=0.8 J/K,g取10 m/s2.活塞厚度及活塞与汽缸壁的摩擦忽略不计,活塞始终与汽缸壁垂直且不漏气.当电热丝通电加热时,活塞缓慢到达汽缸口.
(1)加热过程气体压强 (选填“增大”“减小”或“不变”),汽缸内壁单位面积单位时间内受到分子的撞击数 (选填“增大”“减小”或“不变”);
(2)求加热前汽缸内气体的压强p1;
(3)求加热过程汽缸内气体吸收的热量Q.
参考答案与详细解析
1.(1)60 cm (2)481.7 K (3)325 K
[解析] (1)若将玻璃管自由释放,不计阻力,则整体做自由落体运动,封闭气体的压强为p0=75 cmHg,根据玻意耳定律有p1Sa=p0Sa'
又p1=p0+ρgh=90 cmHg
解得稳定后管内封闭空气柱的长度为a'=60 cm
(2)温度升高,封闭气体压强不变,体积增大,水银柱升高,当水银柱上升至管口时,温度继续升高,水银开始逸出,气体压强减小.设温度为T1时,管内剩余水银柱高度为h',此时不用再升高温度,水银可自动从管中溢出,根据理想气体状态方程有=
可以使水银全部溢出时T1最大,则应最大,代入数据得h'=10 cm
解得T1≈481.7 K
故温度至少升到481.7 K时,可使管内水银柱全部溢出.
(3)若玻璃管长为L3=65 cm,同理,设管内剩内水银柱为h″时处于临界状态,水银自动溢出,根据理想气体状态方程有
=
代入数据解得h″=-5,而h″≥0,故h″取0
解得T2≈325 K
故温度至少升到325 K时,可使管内水银柱全部溢出.
2.(1)负 不变 (2)10 kg (3)2200 cm3
[解析] (1)活塞下降过程中,气体体积减小,被封闭空气对外做负功,被封闭空气待温度稳定后,由于汽缸导热良好,温度不变,封闭的空气可视为理想气体,其内能将不变.
(2)对活塞进行分析有
mg+p0S1=p1S1
汽缸导热良好,温度不变,即气体发生的是等温变化,根据玻意耳定律有
p0=p1[(L1-h1)S1+L2S2]
解得m=10 kg.
(3)再次平衡时,根据玻意耳定律有
p0=p1[(L1-h2)S1+L2S2-V]
解得V=2200 cm3.
3.(1)p0 (2)H (3)2p0
[解析] (1)对活塞受力分析,由平衡条件得
p0S+Mg=p1S
解得p1=p0
(2)第一次充气时,对充进部分的气体研究,有
p0=p1
解得h1=H
(3)活塞与汽缸挡柱刚好接触时,有
n==30次
则充气的前30次气体做等压变化,后15次压强变化,有
p1S=p2HS
解得p2=2p0
4.(1)不变 (2)1.1×105 Pa 300 K (3)36 J
[解析] (1)对汽缸受力分析,变化前有Mg+p0S=p1S,变化后有Mg+p0S=p1'S,可知p1=p1',则可知,环境温度由T1缓慢升高到T2过程中,汽缸内气体压强不变.
(2)以汽缸为研究对象,根据平衡条件可知
Mg+p0S=p1S
解得p1=1.1×105 Pa
气体升温膨胀过程为等压过程,由盖-吕萨克定律有
=
解得T2=300 K.
(3)由热力学第一定律可知ΔU=W+Q
气体膨胀对外做功,则可得
W=-p1Sh=-11 J
所以气体需要从外界吸收热量Q=36 J.
5.(1)不变 减小 (2)8.5×104 Pa (3)83.4 J
[解析] (1)加热过程,活塞、汽缸和重物整体受力不变,汽缸向下滑动,活塞的受力不变,即气体对活塞的压力不变,气体的压强不变;加热过程,气体的温度升高,气体的平均动能增大,气体分子对汽缸内壁的平均作用力变大,但是气体的压强不变,即单位面积单位时间内气体分子的作用力不变,则汽缸内壁单位面积单位时间内受到分子的撞击数减小.
(2)活塞受力平衡,有
FT+p1S=mgsin θ+p0S
重物受力平衡,有FT=Mg
可得气体压强p1=p0+=8.5×104 Pa.
(3)加热过程为等压变化,满足=
得T1=400 K
气体内能变化ΔU=ΔEk=80 J
气体对外做功W=-p1S=-3.4 J
根据热力学第一定律ΔU=W+Q
可得Q=83.4 J.
同课章节目录
