人教版六年级上册数学6.2《稍复杂的分数乘法问题(一)》课件(共15张PPT)
文档属性
| 名称 | 人教版六年级上册数学6.2《稍复杂的分数乘法问题(一)》课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 15:48:44 | ||
图片预览





文档简介
(共15张PPT)
稍复杂的分数乘法问题(一)
根据这些信息,你能提出什么问题?
先行组织
作业设计
成果集成
迁移运用
新知建构
从图中,你知道了哪些数学信息?
分析:
2号坑的占地面积是多少平方米?
从信息窗中寻找解决问题所需要的信息,分析并找出数量关系。
你能解决这个问题了吗?
1号坑和3号坑共占
三个坑总占地面积约20000平方米。
2号坑的面积=总面积-1号坑和3号坑的面积和
2号坑的面积=总面积×2号坑占总面积的几分之几
先行组织
作业设计
成果集成
迁移运用
新知建构
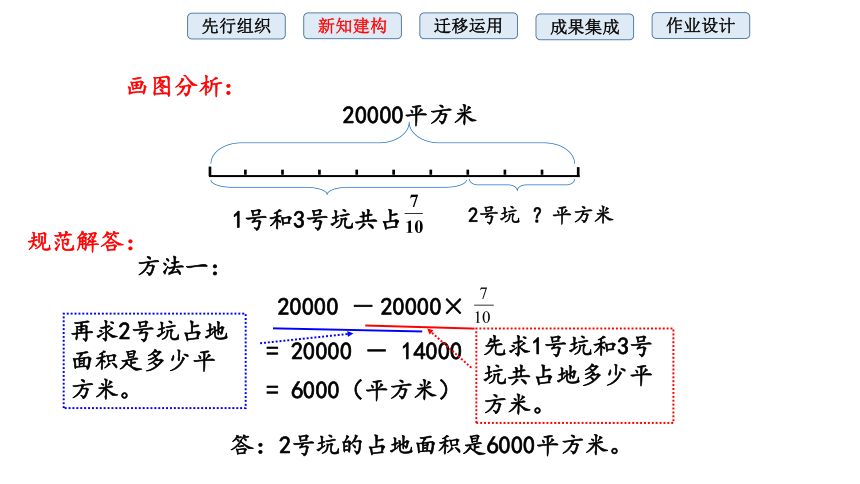
画图分析:
规范解答:
方法一:
20000平方米
2号坑 ?平方米
1号和3号坑共占
20000×
= 20000 - 14000
答:2号坑的占地面积是6000平方米。
20000 -
先求1号坑和3号坑共占地多少平方米。
再求2号坑占地面积是多少平方米。
= 6000(平方米)
先行组织
作业设计
成果集成
迁移运用
新知建构
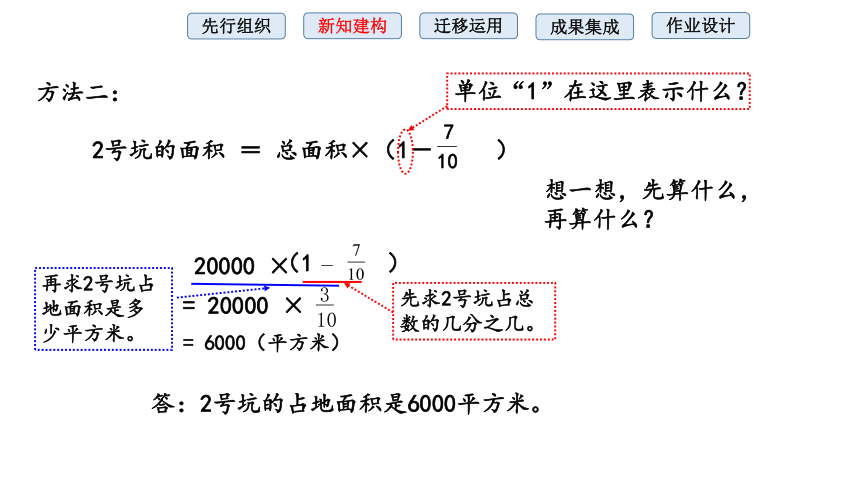
方法二:
想一想,先算什么,再算什么?
2号坑的面积 = 总面积×(1- )
10
7
单位“1”在这里表示什么?
(1 )
= 20000 ×
答:2号坑的占地面积是6000平方米。
20000 ×
先求2号坑占总数的几分之几。
再求2号坑占地面积是多少平方米。
= 6000(平方米)
10
3
先行组织
作业设计
成果集成
迁移运用
新知建构
-
把3个坑的总占地面积看作单位“1”,“2号坑的占地面积”与“3个坑的总占地面积”之间的关系,即整体与部分之间的数量关系,引入分数乘减混合运算的学习。
确定单位“1”是解分数应用题的关键,这本书的总页数是单位“1”。
我已经读了这本书的 。
共80页
还剩多少页没有读?
思路1:剩下的页数=总页数-读过的页数。
思路2:剩下的页数=总页数×( )。
先行组织
作业设计
成果集成
迁移运用
新知建构
方法一:
方法二:
=32(页)
答:还剩32页没有读。
=80 ×
=32(页)
先行组织
作业设计
成果集成
迁移运用
新知建构
例题1
学校图书室新进156本书,一班借走 ,二班借走余下的 ,还剩多少本书?
分析:第一步把新进书的总数看作单位“1”;第二步把一班借走后余下的本数看作单位“1”。
先行组织
作业设计
成果集成
迁移运用
新知建构
规范解答:
方法一:(分步解答)
方法二:(列综合算式解答)
先行组织
作业设计
成果集成
迁移运用
新知建构
例题2
规范解答:
一袋大米15千克,先用去它的 ,又用去它的 千克,现在还有大米多少千克?
错解:
分析:错解中把 当作 千克计算。而 是指用去的占一袋大米总量的 ,不是用去大米的千克数。应先算出这部分大米的千克数的多少。
先行组织
作业设计
成果集成
迁移运用
新知建构
稍复杂的分数乘法问题一
已知总量和其中一部分量占总量的几分之几,求另一部分量的方法:
方法一:另一部分量=总量-总量×一部分量的分率
方法二:另一部分量=总量×(1-一部分量的分率)
关键:
2. 找准分率和量的对应关系。
1. 找准单位“1”。
分数乘减混合运算的运算顺序:
先算乘法,再算减法。
有括号先算括号里面的。
先行组织
作业设计
成果集成
迁移运用
新知建构
1. 找出单位“1”,并说说两个量之间又怎样的数量关系?
(1)白兔的只数占兔子总只数的 。
(2)果园里苹果树的棵树是梨树棵树的 。
兔子总只数是单位“1”
梨树棵数是单位“1”
兔子总只数 =白兔的只数
梨树棵数 =苹果树的棵数
先行组织
作业设计
成果集成
迁移运用
新知建构
2.
六年级一班有48名同学,其中 的人体育类社团 ,剩下的参加艺术类社团。参加艺术类社团的有多少人?
规范解答:
先行组织
作业设计
成果集成
迁移运用
新知建构
答:参加艺术类社团的有36人。
90× + 90×
=30+27
=57(只)
答:两个年级一共折了57只。
90×( + )
=90×
=57(只)
答:两个年级一共折了57只。
3.
一共90只
五年级折了其中的 。
四年级折了其中的 。
两个年级一共折了多少只?
规范解答:
先行组织
作业设计
成果集成
迁移运用
新知建构
规范解答:
4. 一桶油重2千克,第一次倒出总数的 后,第二次倒出 千克,还剩多少千克?
答:还剩 千克。
先行组织
作业设计
成果集成
迁移运用
新知建构
稍复杂的分数乘法问题(一)
根据这些信息,你能提出什么问题?
先行组织
作业设计
成果集成
迁移运用
新知建构
从图中,你知道了哪些数学信息?
分析:
2号坑的占地面积是多少平方米?
从信息窗中寻找解决问题所需要的信息,分析并找出数量关系。
你能解决这个问题了吗?
1号坑和3号坑共占
三个坑总占地面积约20000平方米。
2号坑的面积=总面积-1号坑和3号坑的面积和
2号坑的面积=总面积×2号坑占总面积的几分之几
先行组织
作业设计
成果集成
迁移运用
新知建构
画图分析:
规范解答:
方法一:
20000平方米
2号坑 ?平方米
1号和3号坑共占
20000×
= 20000 - 14000
答:2号坑的占地面积是6000平方米。
20000 -
先求1号坑和3号坑共占地多少平方米。
再求2号坑占地面积是多少平方米。
= 6000(平方米)
先行组织
作业设计
成果集成
迁移运用
新知建构
方法二:
想一想,先算什么,再算什么?
2号坑的面积 = 总面积×(1- )
10
7
单位“1”在这里表示什么?
(1 )
= 20000 ×
答:2号坑的占地面积是6000平方米。
20000 ×
先求2号坑占总数的几分之几。
再求2号坑占地面积是多少平方米。
= 6000(平方米)
10
3
先行组织
作业设计
成果集成
迁移运用
新知建构
-
把3个坑的总占地面积看作单位“1”,“2号坑的占地面积”与“3个坑的总占地面积”之间的关系,即整体与部分之间的数量关系,引入分数乘减混合运算的学习。
确定单位“1”是解分数应用题的关键,这本书的总页数是单位“1”。
我已经读了这本书的 。
共80页
还剩多少页没有读?
思路1:剩下的页数=总页数-读过的页数。
思路2:剩下的页数=总页数×( )。
先行组织
作业设计
成果集成
迁移运用
新知建构
方法一:
方法二:
=32(页)
答:还剩32页没有读。
=80 ×
=32(页)
先行组织
作业设计
成果集成
迁移运用
新知建构
例题1
学校图书室新进156本书,一班借走 ,二班借走余下的 ,还剩多少本书?
分析:第一步把新进书的总数看作单位“1”;第二步把一班借走后余下的本数看作单位“1”。
先行组织
作业设计
成果集成
迁移运用
新知建构
规范解答:
方法一:(分步解答)
方法二:(列综合算式解答)
先行组织
作业设计
成果集成
迁移运用
新知建构
例题2
规范解答:
一袋大米15千克,先用去它的 ,又用去它的 千克,现在还有大米多少千克?
错解:
分析:错解中把 当作 千克计算。而 是指用去的占一袋大米总量的 ,不是用去大米的千克数。应先算出这部分大米的千克数的多少。
先行组织
作业设计
成果集成
迁移运用
新知建构
稍复杂的分数乘法问题一
已知总量和其中一部分量占总量的几分之几,求另一部分量的方法:
方法一:另一部分量=总量-总量×一部分量的分率
方法二:另一部分量=总量×(1-一部分量的分率)
关键:
2. 找准分率和量的对应关系。
1. 找准单位“1”。
分数乘减混合运算的运算顺序:
先算乘法,再算减法。
有括号先算括号里面的。
先行组织
作业设计
成果集成
迁移运用
新知建构
1. 找出单位“1”,并说说两个量之间又怎样的数量关系?
(1)白兔的只数占兔子总只数的 。
(2)果园里苹果树的棵树是梨树棵树的 。
兔子总只数是单位“1”
梨树棵数是单位“1”
兔子总只数 =白兔的只数
梨树棵数 =苹果树的棵数
先行组织
作业设计
成果集成
迁移运用
新知建构
2.
六年级一班有48名同学,其中 的人体育类社团 ,剩下的参加艺术类社团。参加艺术类社团的有多少人?
规范解答:
先行组织
作业设计
成果集成
迁移运用
新知建构
答:参加艺术类社团的有36人。
90× + 90×
=30+27
=57(只)
答:两个年级一共折了57只。
90×( + )
=90×
=57(只)
答:两个年级一共折了57只。
3.
一共90只
五年级折了其中的 。
四年级折了其中的 。
两个年级一共折了多少只?
规范解答:
先行组织
作业设计
成果集成
迁移运用
新知建构
规范解答:
4. 一桶油重2千克,第一次倒出总数的 后,第二次倒出 千克,还剩多少千克?
答:还剩 千克。
先行组织
作业设计
成果集成
迁移运用
新知建构
