6.1.1 菱形的性质(学案,有答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
6.1.1 菱形的性质(学案,有答案)
列清单·划重点
知识点1 菱形的定义
有一组___________相等的_________四边形叫做菱形.
知识点2 菱形的性质
1.一般性质:菱形具有____________的所有性质.
2.特殊性质:
(1)定理1:菱形的四条边___________.
几何语言:如图所示,
∵四边形ABCD是______________,
(2)定理2:菱形的对角线___________.
几何语言:如图所示,
∵四边形 ABCD是___________,
3.对称性:菱形既是_________图形,对称中心是_________的交点;又是_______图形,有________条对称轴,分别是两条___________所在的直线.
知识点3 菱形的面积
明考点·识方法
考点1 菱形的定义及对称性
典例1 如图,在平行四边形 ABCD中, 将线段AB水平向右平移个单位长度得到线段 EF,若四边形 ECDF 为菱形时,则 a的值为___________.
思路导析 由菱形的定义可知,当CD=CE=4时,平行四边形ECDF为菱形,进而可求得a的值.
变式 点 E 是菱形ABCD 的对称中心,∠B=56°,连接 AE,则∠BAE的度数为___________.
考点2 菱形边的性质
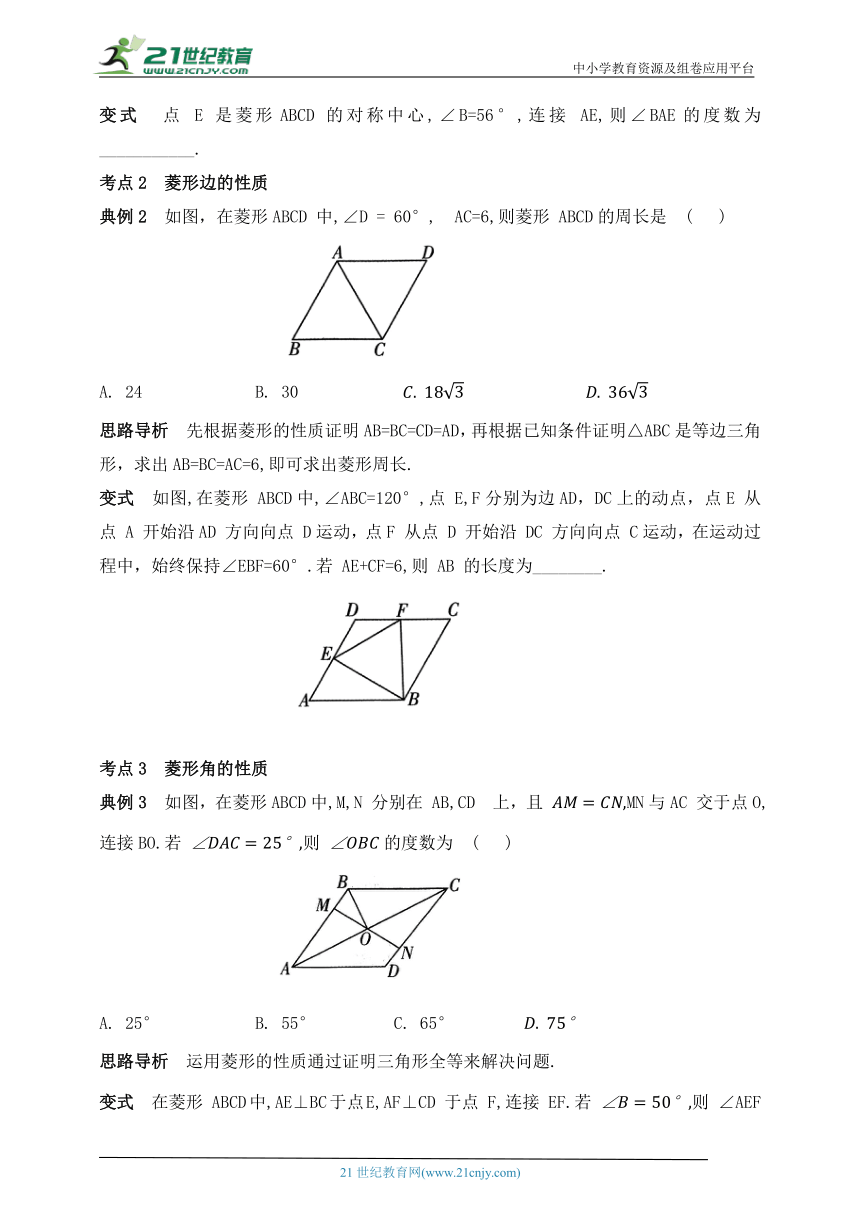
典例2 如图,在菱形ABCD 中,∠D = 60°, AC=6,则菱形 ABCD的周长是 ( )
A. 24 B. 30
思路导析 先根据菱形的性质证明AB=BC=CD=AD,再根据已知条件证明△ABC是等边三角形,求出AB=BC=AC=6,即可求出菱形周长.
变式 如图,在菱形 ABCD中,∠ABC=120°,点 E,F分别为边AD,DC上的动点,点E 从点 A 开始沿AD 方向向点 D运动,点F 从点 D 开始沿 DC 方向向点 C运动,在运动过程中,始终保持∠EBF=60°.若 AE+CF=6,则 AB 的长度为________.
考点3 菱形角的性质
典例3 如图,在菱形ABCD中,M,N 分别在 AB,CD 上,且 MN与AC 交于点O,连接BO.若 则 的度数为 ( )
A. 25° B. 55° C. 65°
思路导析 运用菱形的性质通过证明三角形全等来解决问题.
变式 在菱形 ABCD中,AE⊥BC于点E,AF⊥CD 于点 F,连接 EF.若 则 ∠AEF 的度数为___________.
考点4 菱形对角线的性质
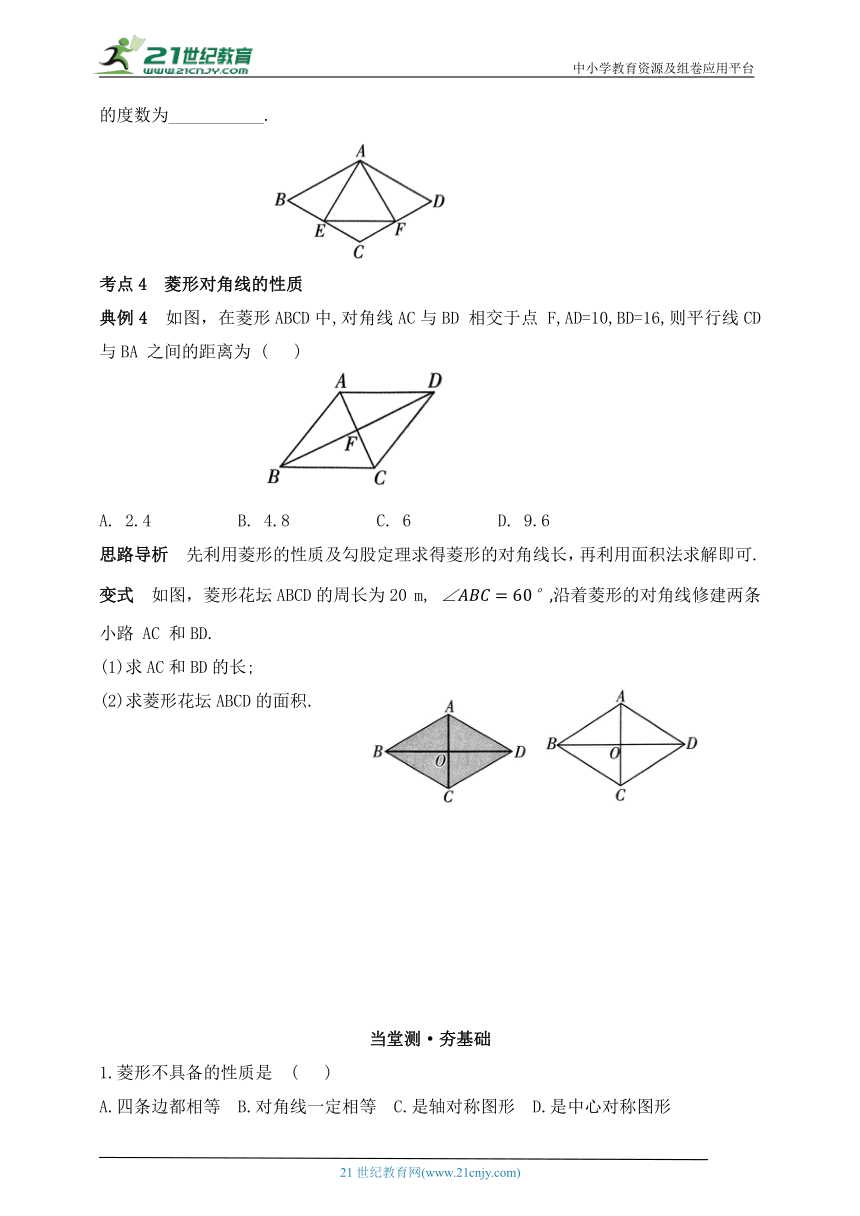
典例4 如图,在菱形ABCD中,对角线AC与BD 相交于点 F,AD=10,BD=16,则平行线CD与BA 之间的距离为 ( )
A. 2.4 B. 4.8 C. 6 D. 9.6
思路导析 先利用菱形的性质及勾股定理求得菱形的对角线长,再利用面积法求解即可.
变式 如图,菱形花坛ABCD的周长为20 m, 沿着菱形的对角线修建两条小路 AC 和BD.
(1)求AC和BD的长;
(2)求菱形花坛ABCD的面积.
当堂测·夯基础
1.菱形不具备的性质是 ( )
A.四条边都相等 B.对角线一定相等 C.是轴对称图形 D.是中心对称图形
2.如图,在菱形 ABCD 中,若则菱形 ABCD的周长为 ( )
A. 32 C. 16
3.如图,四边形ABCD是菱形,B,C,D 三点坐标分别是(2,0),(m,0),(10,4),点 A 在第一象限,则m 的值是___________.
第3题图 第4题图
4.如图,菱形 ABCD的面积为24,点 E 是AB 的中点,点 F 是 BC 上的动点.若 的面积为4,则图中阴影部分的面积为____________.
5.如图,菱形ABCD中,点E,F分别是AB,BC边上的点,BF,求证:
参考答案
【列清单·划重点】
知识点1 邻边 平行
知识点2 1.平行四边形
2.(1)都相等 菱形 (2)互相垂直 菱形
3.中心对称 对角线 轴对称 2 对角线
知识点3
1. DH BD 2. 2 4
【明考点·识方法】
典例1 2
解析:∵四边形 ABCD是平行四边形,∴AB∥CD,CE∥FD,CD=AB=4,
∵将线段AB 水平向右平移得到线段EF,∴AB∥EF∥CD,
∴四边形 ECDF 为平行四边形,
当CD=CE=4时,平行四边形 ECDF 为菱形,此时a=BE=BC-CE=6-4=2.
变式 62°
典例2 A
变式 6
典例3 C
解析:∵四边形ABCD 为菱形,∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中, ∴△AMO≌△CNO(ASA),∴AO=CO,
∵AB=BC,∴BO⊥AC,∴∠BOC=90°,
∵∠DAC=25°,∴∠BCA=∠DAC=25°,∴∠OBC=90°-25°=65°.
变式 65°
典例4 D
变式
解:(1)∵四边形 ABCD 是菱形,∴AB = BC = 5 m,AC⊥ BD, AC =2OA,BD=2OB,
∵∠ABC=60°,∴△ABC是等边三角形,∴AC=AB=5m,
(2)菱形花坛 ABCD 的面积
【当堂测·夯基础】
1. B 2. A 3. 7 4. 10
5.证明:∵四边形ABCD 是菱形,∴AB=BC=CD=AD,∠A=∠C,
∵BE=BF,∴AB-BE=BC-BF,∴AE=CF,
在△DAE 和△DCF中,∴△DAE≌△DCF(SAS),
∴DE=DF,∴∠DEF=∠DFE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.1.1 菱形的性质(学案,有答案)
列清单·划重点
知识点1 菱形的定义
有一组___________相等的_________四边形叫做菱形.
知识点2 菱形的性质
1.一般性质:菱形具有____________的所有性质.
2.特殊性质:
(1)定理1:菱形的四条边___________.
几何语言:如图所示,
∵四边形ABCD是______________,
(2)定理2:菱形的对角线___________.
几何语言:如图所示,
∵四边形 ABCD是___________,
3.对称性:菱形既是_________图形,对称中心是_________的交点;又是_______图形,有________条对称轴,分别是两条___________所在的直线.
知识点3 菱形的面积
明考点·识方法
考点1 菱形的定义及对称性
典例1 如图,在平行四边形 ABCD中, 将线段AB水平向右平移个单位长度得到线段 EF,若四边形 ECDF 为菱形时,则 a的值为___________.
思路导析 由菱形的定义可知,当CD=CE=4时,平行四边形ECDF为菱形,进而可求得a的值.
变式 点 E 是菱形ABCD 的对称中心,∠B=56°,连接 AE,则∠BAE的度数为___________.
考点2 菱形边的性质
典例2 如图,在菱形ABCD 中,∠D = 60°, AC=6,则菱形 ABCD的周长是 ( )
A. 24 B. 30
思路导析 先根据菱形的性质证明AB=BC=CD=AD,再根据已知条件证明△ABC是等边三角形,求出AB=BC=AC=6,即可求出菱形周长.
变式 如图,在菱形 ABCD中,∠ABC=120°,点 E,F分别为边AD,DC上的动点,点E 从点 A 开始沿AD 方向向点 D运动,点F 从点 D 开始沿 DC 方向向点 C运动,在运动过程中,始终保持∠EBF=60°.若 AE+CF=6,则 AB 的长度为________.
考点3 菱形角的性质
典例3 如图,在菱形ABCD中,M,N 分别在 AB,CD 上,且 MN与AC 交于点O,连接BO.若 则 的度数为 ( )
A. 25° B. 55° C. 65°
思路导析 运用菱形的性质通过证明三角形全等来解决问题.
变式 在菱形 ABCD中,AE⊥BC于点E,AF⊥CD 于点 F,连接 EF.若 则 ∠AEF 的度数为___________.
考点4 菱形对角线的性质
典例4 如图,在菱形ABCD中,对角线AC与BD 相交于点 F,AD=10,BD=16,则平行线CD与BA 之间的距离为 ( )
A. 2.4 B. 4.8 C. 6 D. 9.6
思路导析 先利用菱形的性质及勾股定理求得菱形的对角线长,再利用面积法求解即可.
变式 如图,菱形花坛ABCD的周长为20 m, 沿着菱形的对角线修建两条小路 AC 和BD.
(1)求AC和BD的长;
(2)求菱形花坛ABCD的面积.
当堂测·夯基础
1.菱形不具备的性质是 ( )
A.四条边都相等 B.对角线一定相等 C.是轴对称图形 D.是中心对称图形
2.如图,在菱形 ABCD 中,若则菱形 ABCD的周长为 ( )
A. 32 C. 16
3.如图,四边形ABCD是菱形,B,C,D 三点坐标分别是(2,0),(m,0),(10,4),点 A 在第一象限,则m 的值是___________.
第3题图 第4题图
4.如图,菱形 ABCD的面积为24,点 E 是AB 的中点,点 F 是 BC 上的动点.若 的面积为4,则图中阴影部分的面积为____________.
5.如图,菱形ABCD中,点E,F分别是AB,BC边上的点,BF,求证:
参考答案
【列清单·划重点】
知识点1 邻边 平行
知识点2 1.平行四边形
2.(1)都相等 菱形 (2)互相垂直 菱形
3.中心对称 对角线 轴对称 2 对角线
知识点3
1. DH BD 2. 2 4
【明考点·识方法】
典例1 2
解析:∵四边形 ABCD是平行四边形,∴AB∥CD,CE∥FD,CD=AB=4,
∵将线段AB 水平向右平移得到线段EF,∴AB∥EF∥CD,
∴四边形 ECDF 为平行四边形,
当CD=CE=4时,平行四边形 ECDF 为菱形,此时a=BE=BC-CE=6-4=2.
变式 62°
典例2 A
变式 6
典例3 C
解析:∵四边形ABCD 为菱形,∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中, ∴△AMO≌△CNO(ASA),∴AO=CO,
∵AB=BC,∴BO⊥AC,∴∠BOC=90°,
∵∠DAC=25°,∴∠BCA=∠DAC=25°,∴∠OBC=90°-25°=65°.
变式 65°
典例4 D
变式
解:(1)∵四边形 ABCD 是菱形,∴AB = BC = 5 m,AC⊥ BD, AC =2OA,BD=2OB,
∵∠ABC=60°,∴△ABC是等边三角形,∴AC=AB=5m,
(2)菱形花坛 ABCD 的面积
【当堂测·夯基础】
1. B 2. A 3. 7 4. 10
5.证明:∵四边形ABCD 是菱形,∴AB=BC=CD=AD,∠A=∠C,
∵BE=BF,∴AB-BE=BC-BF,∴AE=CF,
在△DAE 和△DCF中,∴△DAE≌△DCF(SAS),
∴DE=DF,∴∠DEF=∠DFE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
