6.1.2 菱形的判定(学案,有答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
6.1.2 菱形的判定(学案,有答案)
列清单·划重点
知识点1 菱形的判定
1.定义法:有一组____________相等的平行四边形是菱形.
几何语言:如图所示,
∵四边形 ABCD 是平行四边形且
∴平行四边形 ABCD 是菱形.
2.定理1:对角线__________的平行四边形是菱形.
几何语言:如图所示,
∵四边形 ABCD 是平行四边形且__________,
∴平行四边形ABCD 是菱形.
3.定理2:四条边都____________的四边形是菱形.
几何语言:如图所示,
∵____________________,∴四边形 ABCD 是菱形.
规律总结
判定菱形的基本思路:
四条边都相等
(1)一般四边形菱形.
(2)
知识点2 菱形的性质和判定
1.连接对角线构造等腰三角形或直角三角形.
2.作高构造直角三角形.
明考点·识方法
考点1 根据菱形的定义进行判定
典例 1 如图,在中,对角线 AC 与 BD 相交于点O,点 E,F 在BD 上,BE=EF=FD,且AC 平分∠EAF,连接CE,CF.
(1)求证:四边形 AECF 是菱形;
(2)若△ABC 的周长为36,BD=24,则四边形 AECF 的面积为_____________.
思路导析 (1)由平行四边形的性质可得OA=OC,OB=OD,又根据BE=FD,可得OE=OF,可证四边形AECF是平行四边形,由平行线的性质和角平分线的定义可证AE=CE,即可得结论;
(2)由菱形的性质可得AC⊥EF,AO=CO,EO=FO,可得AB=BC,由勾股定理可求AO的长,由菱形的面积公式即可求解.
变式 如图,已知点 A,D,C,B在同一条直线上,且 AD=BC,AE=BF,CE=DF.
(1)求证:AE∥BF;
(2)若DF=FC时,求证:四边形 DECF 是菱形.
考点2 根据菱形的边进行判定
典例2 在一次数学实践探究活动中,某兴趣小组将一张平行四边形纸片ABCD 进行折叠,折痕为AE,点 E 在 BC 边上,点 B 落在点 F 处.当点 F恰好落在AD 边上时,求证:四边形 ABEF是菱形.
思路导析 根据四条边相等的四边形是菱形进行判定即可.
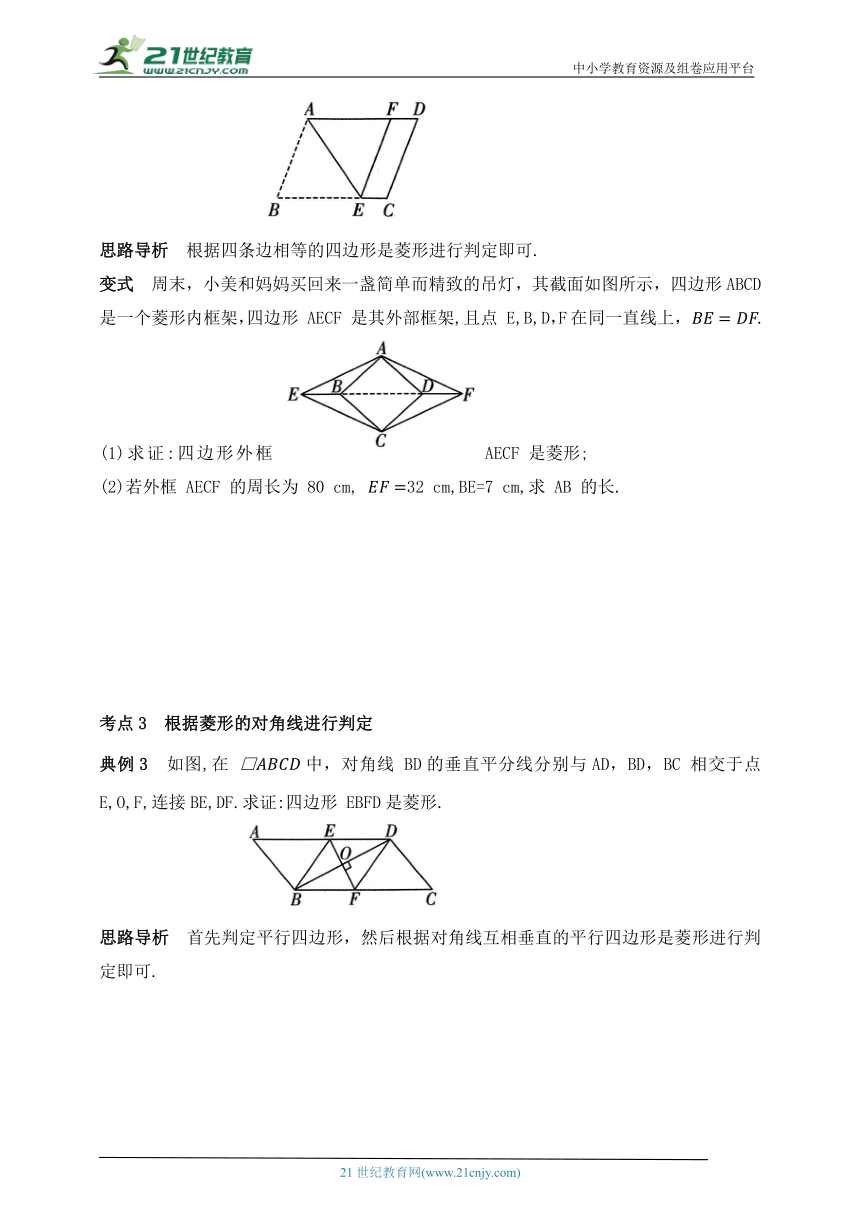
变式 周末,小美和妈妈买回来一盏简单而精致的吊灯,其截面如图所示,四边形ABCD是一个菱形内框架,四边形 AECF 是其外部框架,且点 E,B,D,F在同一直线上,
(1)求证:四边形外框 AECF 是菱形;
(2)若外框 AECF 的周长为 80 cm, 32 cm,BE=7 cm,求 AB 的长.
考点3 根据菱形的对角线进行判定
典例3 如图,在 中,对角线 BD的垂直平分线分别与AD,BD,BC 相交于点 E,O,F,连接BE,DF.求证:四边形 EBFD是菱形.
思路导析 首先判定平行四边形,然后根据对角线互相垂直的平行四边形是菱形进行判定即可.
变式 如图,在 中,对角线AC 与 BD 相交于点O,过点 O的直线EF 与BA,DC的延长线分别交于点E,F.
(1)求证:
(2)请再添加一个条件,使四边形 BFDE 是菱形,并说明理由.
考点4 菱形性质与判定的综合应用
典例4 如图,在平行四边形 ABCD 中,点 F 在边AD上, 连接BF,点O为BF 的中点,AO的延长线交边BC 于点 E, 连接EF.
(1)求证:四边形 ABEF 是菱形;
(2)若平行四边形 ABCD 的周长为22,求AE的长.
思路导析 (1)根据邻边相等的平行四边形是菱形证明即可;(2)证明 是等边三角形,求出AB 可得结论.
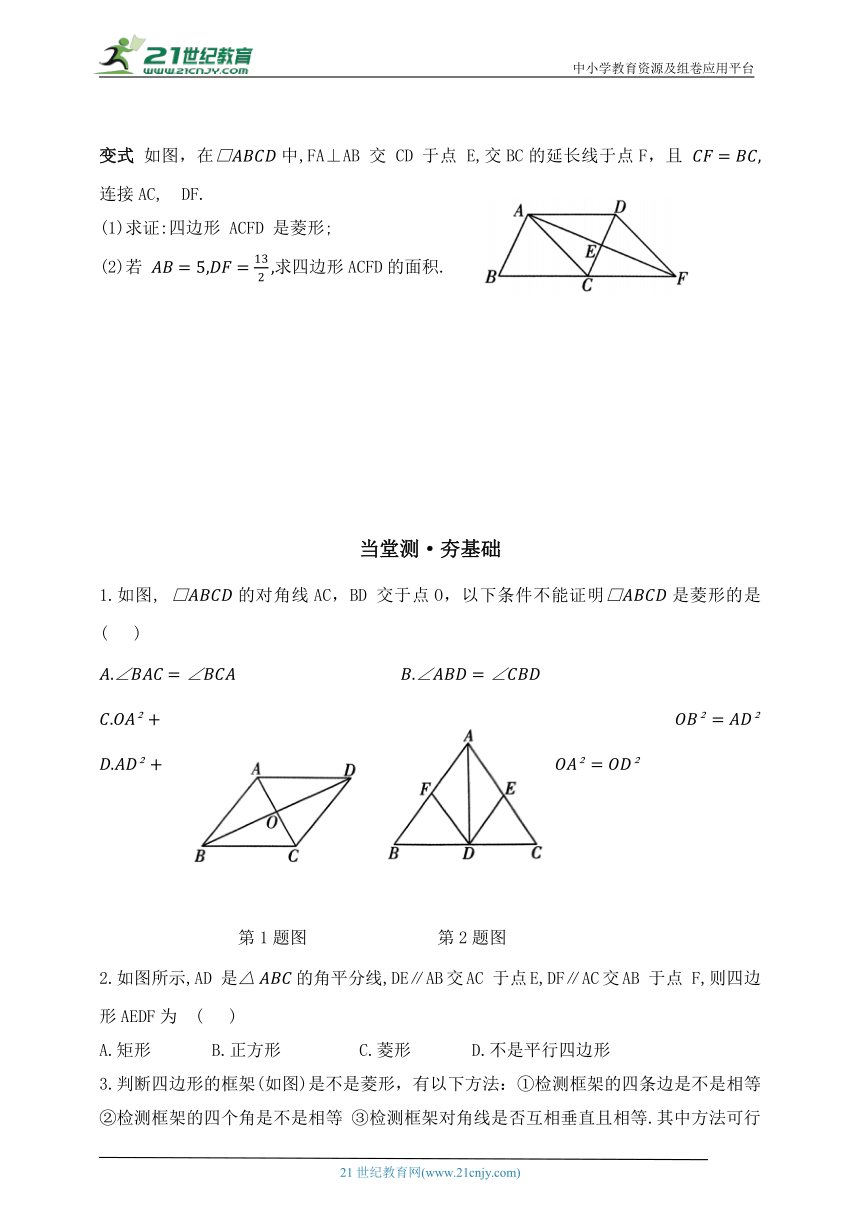
变式 如图,在中,FA⊥AB 交 CD 于点 E,交BC的延长线于点F,且 连接AC, DF.
(1)求证:四边形 ACFD 是菱形;
(2)若 求四边形ACFD的面积.
当堂测·夯基础
1.如图, 的对角线AC,BD 交于点O,以下条件不能证明是菱形的是 ( )
第1题图 第2题图
2.如图所示,AD 是的角平分线,DE∥AB交AC 于点E,DF∥AC交AB 于点 F,则四边形AEDF为 ( )
A.矩形 B.正方形 C.菱形 D.不是平行四边形
3.判断四边形的框架(如图)是不是菱形,有以下方法:①检测框架的四条边是不是相等 ②检测框架的四个角是不是相等 ③检测框架对角线是否互相垂直且相等.其中方法可行的是 ( )
A. ① B. ② C. ①③ D. ②③
第3题图 第4 题图
4.如图,在△ABC中,AD,CD分别平分∠BAC 和∠ACB,AE∥CD,CE∥AD.若从三个条件:①AB=AC ②AB=BC ③AC=BC中,选择一个作为已知条件,则能使四边形 ADCE 为菱形的是___________.(填序号)
参考答案
【列清单·划重点】
知识点1 1.邻边
2.互相垂直 AC⊥BD
3.相等 AB=BC=CD=DA
【明考点·识方法】
典例1 解:(1)证明:∵四边形 ABCD 是平行四边形,∴OA=OC,OB=OD,
又∵BE=FD,∴OB-BE=OD-FD.∴OE=OF,∴四边形 AECF 是平行四边形,
∴AF∥EC,∴∠FAC=∠ECA,
又∵AC平分∠EAF,∴∠EAC=∠FAC,∴∠EAC=∠ECA,∴AE=CE,
∴四边形 AECF 是菱形;
(2)∵四边形 AECF 是菱形,∴AC⊥EF,AO=CO,EO=FO,∴AB=BC,
∵四边形ABCD 是平行四边形,BD=24,∴BO=DO=12,
∵△ABC的周长为36,∴AB+AO=18,
∴AO=5,∴AC=10,
∵BE=EF=FD,∴EF=8,∴四边形AECF 的面积
故答案为:40.
变式 证明:(1)∵AD=BC,∴AD+CD=BC+CD,∴AC=BD,
∵AE=BF,CE=DF,∴△AEC≌△BFD(SSS),∴∠A=∠B,∴AE∥BF;
(2)∵△AEC≌△BFD,∴∠ECA=∠FDB,∴EC∥DF,
∵EC=DF,∴四边形 DECF 是平行四边形,
∵DF=FC,∴四边形 DECF 是菱形.
典例2 证明:由折叠可知,△AEF 与△AEB 关于AE 对称,
∴AF=AB,EF=EB,∠FAE=∠BAE,
∵四边形 ABCD 是平行四边形,∴AD∥BC,
∵点E在BC 边上,点 F 落在AD 边上,∴AF∥BE,∴∠FAE=∠AEB,
∴∠BAE=∠AEB,∴AB=EB,∴AB=EB=EF=AF,
故四边形 ABEF 是菱形.
变式 解:(1)证明:∵四边形 ABCD 是菱形,
∴AB=AD=BC=CD,∠ABD=∠CBD=∠ADB=∠CDB,
∴∠ABE=∠ADF=∠EBC=∠CDF,
在△ABE与△ADF中,
同理可得. ∴四边形 AECF 是菱形;
(2)连接AC,交 EF 于点O,
∵四边形 AECF 是菱形,外框 AECF 的周长为80 cm,
∴OE=16 cm,OB=16-7=9(cm),
12(cm),
15(cm).
典例3 证明:∵四边形 ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠EDO=∠OBF,
∵O是BD中点,∴BO=DO,
∵∠EOD=∠BOF,在△DEO和△BFO中,
∴△DEO≌△BFO(ASA),∴OE=OF,∴四边形 EBFD 是平行四边形,
又∵EF⊥BD,∴四边形 EBFD是菱形.
变式 证明:(1)∵四边形 ABCD 是平行四边形,∴OA=OC,BE∥DF,∴∠E=∠F,
在△AOE 和△COF 中, ∴△AOE≌△COF(AAS),∴AE=CF;
(2)当 EF⊥BD时,四边形 BFDE 是菱形,(答案不唯一)
理由:如图:连接 BF,DE,
∵四边形ABCD 是平行四边形,∴OB=OD,
∵△AOE≌△COF,∴OE=OF,∴四边形 BFDE 是平行四边形,
∵EF⊥BD,∴四边形 BFDE 是菱形.
典例4 解:(1)证明:∵四边形 ABCD 是平行四边形,
∴AD∥BC,即AF∥BE,∴∠AFB=∠EBF,∠FAE=∠BEA,
∵O为BF的中点,∴BO=FO,∴△AOF≌△EOB(AAS),∴BE=FA,
∵AF∥BE,∴四边形 ABEF 是平行四边形,
又∵AB=AF,∴四边形ABEF 是菱形;
(2)∵AD=BC,AF=BE,∴DF=CE=1,
∵平行四边形ABCD的周长为22,∴菱形ABEF 的周长为22-2=20,
∴AB=20÷4=5,
∵四边形 ABEF 是菱形,
又∵AB=BE,∴△ABE是等边三角形,∴AE=AB=5.
变式 解:(1)证明:∵四边形 ABCD 是平行四边形,∴AD∥BC,AD=BC,
∵点F在BC 的延长线上,且CF=BC,∴AD∥CF,AD=CF,
∴四边形ACFD 是平行四边形,
∵CD∥AB,FA⊥AB交CD 于点E,∴∠CEF=∠BAF=90°,∴FA⊥CD,
∴四边形 ACFD 是菱形;
(2)∵四边形 ACFD 是菱形,CD=AB=5,
∴FA=2FE=12, =30,
∴四边形 ACFD 的面积为 30.
【当堂测·夯基础】
1. D 2. C 3. A 4.②
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.1.2 菱形的判定(学案,有答案)
列清单·划重点
知识点1 菱形的判定
1.定义法:有一组____________相等的平行四边形是菱形.
几何语言:如图所示,
∵四边形 ABCD 是平行四边形且
∴平行四边形 ABCD 是菱形.
2.定理1:对角线__________的平行四边形是菱形.
几何语言:如图所示,
∵四边形 ABCD 是平行四边形且__________,
∴平行四边形ABCD 是菱形.
3.定理2:四条边都____________的四边形是菱形.
几何语言:如图所示,
∵____________________,∴四边形 ABCD 是菱形.
规律总结
判定菱形的基本思路:
四条边都相等
(1)一般四边形菱形.
(2)
知识点2 菱形的性质和判定
1.连接对角线构造等腰三角形或直角三角形.
2.作高构造直角三角形.
明考点·识方法
考点1 根据菱形的定义进行判定
典例 1 如图,在中,对角线 AC 与 BD 相交于点O,点 E,F 在BD 上,BE=EF=FD,且AC 平分∠EAF,连接CE,CF.
(1)求证:四边形 AECF 是菱形;
(2)若△ABC 的周长为36,BD=24,则四边形 AECF 的面积为_____________.
思路导析 (1)由平行四边形的性质可得OA=OC,OB=OD,又根据BE=FD,可得OE=OF,可证四边形AECF是平行四边形,由平行线的性质和角平分线的定义可证AE=CE,即可得结论;
(2)由菱形的性质可得AC⊥EF,AO=CO,EO=FO,可得AB=BC,由勾股定理可求AO的长,由菱形的面积公式即可求解.
变式 如图,已知点 A,D,C,B在同一条直线上,且 AD=BC,AE=BF,CE=DF.
(1)求证:AE∥BF;
(2)若DF=FC时,求证:四边形 DECF 是菱形.
考点2 根据菱形的边进行判定
典例2 在一次数学实践探究活动中,某兴趣小组将一张平行四边形纸片ABCD 进行折叠,折痕为AE,点 E 在 BC 边上,点 B 落在点 F 处.当点 F恰好落在AD 边上时,求证:四边形 ABEF是菱形.
思路导析 根据四条边相等的四边形是菱形进行判定即可.
变式 周末,小美和妈妈买回来一盏简单而精致的吊灯,其截面如图所示,四边形ABCD是一个菱形内框架,四边形 AECF 是其外部框架,且点 E,B,D,F在同一直线上,
(1)求证:四边形外框 AECF 是菱形;
(2)若外框 AECF 的周长为 80 cm, 32 cm,BE=7 cm,求 AB 的长.
考点3 根据菱形的对角线进行判定
典例3 如图,在 中,对角线 BD的垂直平分线分别与AD,BD,BC 相交于点 E,O,F,连接BE,DF.求证:四边形 EBFD是菱形.
思路导析 首先判定平行四边形,然后根据对角线互相垂直的平行四边形是菱形进行判定即可.
变式 如图,在 中,对角线AC 与 BD 相交于点O,过点 O的直线EF 与BA,DC的延长线分别交于点E,F.
(1)求证:
(2)请再添加一个条件,使四边形 BFDE 是菱形,并说明理由.
考点4 菱形性质与判定的综合应用
典例4 如图,在平行四边形 ABCD 中,点 F 在边AD上, 连接BF,点O为BF 的中点,AO的延长线交边BC 于点 E, 连接EF.
(1)求证:四边形 ABEF 是菱形;
(2)若平行四边形 ABCD 的周长为22,求AE的长.
思路导析 (1)根据邻边相等的平行四边形是菱形证明即可;(2)证明 是等边三角形,求出AB 可得结论.
变式 如图,在中,FA⊥AB 交 CD 于点 E,交BC的延长线于点F,且 连接AC, DF.
(1)求证:四边形 ACFD 是菱形;
(2)若 求四边形ACFD的面积.
当堂测·夯基础
1.如图, 的对角线AC,BD 交于点O,以下条件不能证明是菱形的是 ( )
第1题图 第2题图
2.如图所示,AD 是的角平分线,DE∥AB交AC 于点E,DF∥AC交AB 于点 F,则四边形AEDF为 ( )
A.矩形 B.正方形 C.菱形 D.不是平行四边形
3.判断四边形的框架(如图)是不是菱形,有以下方法:①检测框架的四条边是不是相等 ②检测框架的四个角是不是相等 ③检测框架对角线是否互相垂直且相等.其中方法可行的是 ( )
A. ① B. ② C. ①③ D. ②③
第3题图 第4 题图
4.如图,在△ABC中,AD,CD分别平分∠BAC 和∠ACB,AE∥CD,CE∥AD.若从三个条件:①AB=AC ②AB=BC ③AC=BC中,选择一个作为已知条件,则能使四边形 ADCE 为菱形的是___________.(填序号)
参考答案
【列清单·划重点】
知识点1 1.邻边
2.互相垂直 AC⊥BD
3.相等 AB=BC=CD=DA
【明考点·识方法】
典例1 解:(1)证明:∵四边形 ABCD 是平行四边形,∴OA=OC,OB=OD,
又∵BE=FD,∴OB-BE=OD-FD.∴OE=OF,∴四边形 AECF 是平行四边形,
∴AF∥EC,∴∠FAC=∠ECA,
又∵AC平分∠EAF,∴∠EAC=∠FAC,∴∠EAC=∠ECA,∴AE=CE,
∴四边形 AECF 是菱形;
(2)∵四边形 AECF 是菱形,∴AC⊥EF,AO=CO,EO=FO,∴AB=BC,
∵四边形ABCD 是平行四边形,BD=24,∴BO=DO=12,
∵△ABC的周长为36,∴AB+AO=18,
∴AO=5,∴AC=10,
∵BE=EF=FD,∴EF=8,∴四边形AECF 的面积
故答案为:40.
变式 证明:(1)∵AD=BC,∴AD+CD=BC+CD,∴AC=BD,
∵AE=BF,CE=DF,∴△AEC≌△BFD(SSS),∴∠A=∠B,∴AE∥BF;
(2)∵△AEC≌△BFD,∴∠ECA=∠FDB,∴EC∥DF,
∵EC=DF,∴四边形 DECF 是平行四边形,
∵DF=FC,∴四边形 DECF 是菱形.
典例2 证明:由折叠可知,△AEF 与△AEB 关于AE 对称,
∴AF=AB,EF=EB,∠FAE=∠BAE,
∵四边形 ABCD 是平行四边形,∴AD∥BC,
∵点E在BC 边上,点 F 落在AD 边上,∴AF∥BE,∴∠FAE=∠AEB,
∴∠BAE=∠AEB,∴AB=EB,∴AB=EB=EF=AF,
故四边形 ABEF 是菱形.
变式 解:(1)证明:∵四边形 ABCD 是菱形,
∴AB=AD=BC=CD,∠ABD=∠CBD=∠ADB=∠CDB,
∴∠ABE=∠ADF=∠EBC=∠CDF,
在△ABE与△ADF中,
同理可得. ∴四边形 AECF 是菱形;
(2)连接AC,交 EF 于点O,
∵四边形 AECF 是菱形,外框 AECF 的周长为80 cm,
∴OE=16 cm,OB=16-7=9(cm),
12(cm),
15(cm).
典例3 证明:∵四边形 ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠EDO=∠OBF,
∵O是BD中点,∴BO=DO,
∵∠EOD=∠BOF,在△DEO和△BFO中,
∴△DEO≌△BFO(ASA),∴OE=OF,∴四边形 EBFD 是平行四边形,
又∵EF⊥BD,∴四边形 EBFD是菱形.
变式 证明:(1)∵四边形 ABCD 是平行四边形,∴OA=OC,BE∥DF,∴∠E=∠F,
在△AOE 和△COF 中, ∴△AOE≌△COF(AAS),∴AE=CF;
(2)当 EF⊥BD时,四边形 BFDE 是菱形,(答案不唯一)
理由:如图:连接 BF,DE,
∵四边形ABCD 是平行四边形,∴OB=OD,
∵△AOE≌△COF,∴OE=OF,∴四边形 BFDE 是平行四边形,
∵EF⊥BD,∴四边形 BFDE 是菱形.
典例4 解:(1)证明:∵四边形 ABCD 是平行四边形,
∴AD∥BC,即AF∥BE,∴∠AFB=∠EBF,∠FAE=∠BEA,
∵O为BF的中点,∴BO=FO,∴△AOF≌△EOB(AAS),∴BE=FA,
∵AF∥BE,∴四边形 ABEF 是平行四边形,
又∵AB=AF,∴四边形ABEF 是菱形;
(2)∵AD=BC,AF=BE,∴DF=CE=1,
∵平行四边形ABCD的周长为22,∴菱形ABEF 的周长为22-2=20,
∴AB=20÷4=5,
∵四边形 ABEF 是菱形,
又∵AB=BE,∴△ABE是等边三角形,∴AE=AB=5.
变式 解:(1)证明:∵四边形 ABCD 是平行四边形,∴AD∥BC,AD=BC,
∵点F在BC 的延长线上,且CF=BC,∴AD∥CF,AD=CF,
∴四边形ACFD 是平行四边形,
∵CD∥AB,FA⊥AB交CD 于点E,∴∠CEF=∠BAF=90°,∴FA⊥CD,
∴四边形 ACFD 是菱形;
(2)∵四边形 ACFD 是菱形,CD=AB=5,
∴FA=2FE=12, =30,
∴四边形 ACFD 的面积为 30.
【当堂测·夯基础】
1. D 2. C 3. A 4.②
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
