1.4.1角平分线的性质 课件(共27张PPT)
文档属性
| 名称 | 1.4.1角平分线的性质 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-05 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
第一章 直角三角形
1.4.1角平分线的性质
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
在探究角平分线的性质的过程中,发展几何直觉.
提高综合运用三角形全等的有关知识解决问题的能力.
初步了解角的平分线的性质在生活、生产中的应用.
02
新知导入
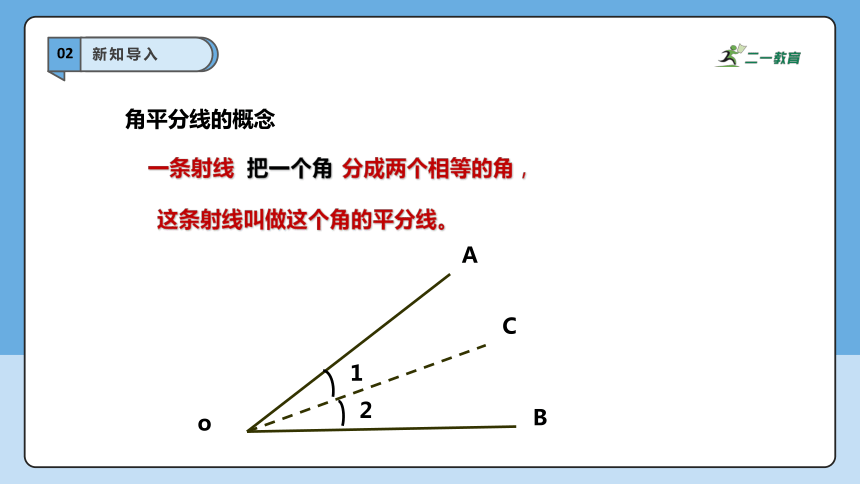
角平分线的概念
一条射线
把一个角
分成两个相等的角,
这条射线叫做这个角的平分线。
o
B
C
A
1
2
03
新知探究
作法:1、以____为圆心,______长为半径作圆弧,与角的两边分别交于M、
N两点;
2、分别以_____ 为圆心,大于__________的长为半径作弧,两条圆弧交于∠AOB内一点____;
3、作射线_____;
_____就是所求作∠AOB的平分线。
点O
任意
M、N
P
OP
OP
A
B
N
M
P
O
尺规作角的平分线
03
新知探究
猜想:
角平分线的性质
折一折
03
新知探究
将AOB对折,在折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么猜想
角平分线上的点到角的两边的距离相等
03
新知探究
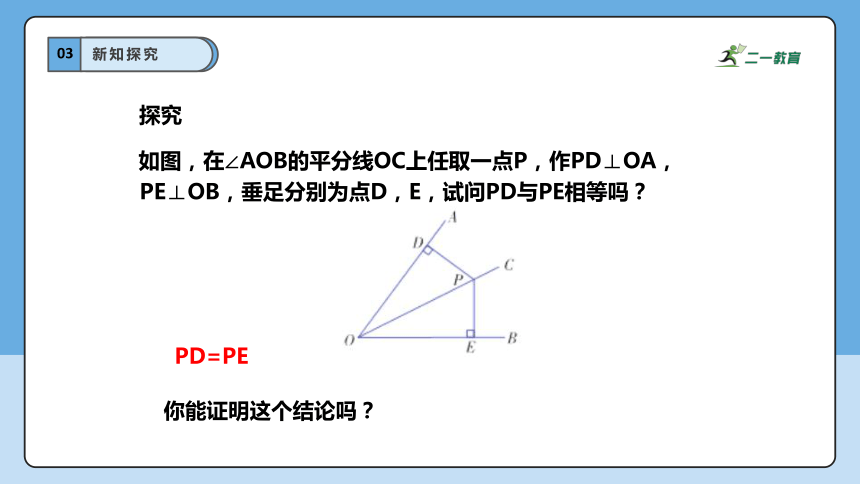
如图,在∠AOB的平分线OC上任取一点P,作PD⊥OA,PE⊥OB,垂足分别为点D,E,试问PD与PE相等吗?
探究
PD=PE
你能证明这个结论吗?
03
新知探究
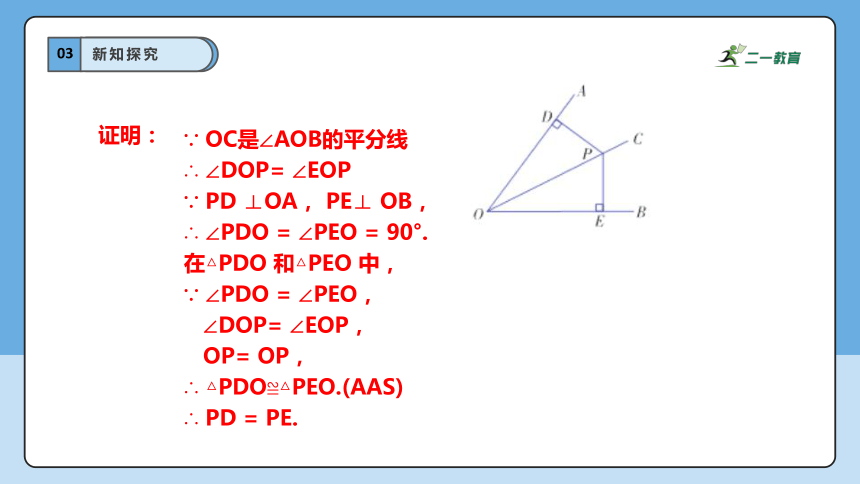
∵ OC是∠AOB的平分线
∴ ∠DOP= ∠EOP
∵ PD ⊥OA, PE⊥ OB,
∴ ∠PDO = ∠PEO = 90°.
在△PDO 和△PEO 中,
∵ ∠PDO = ∠PEO,
∠DOP= ∠EOP,
OP= OP,
∴ △PDO≌△PEO.(AAS)
∴ PD = PE.
证明:
03
新知探究
结论:
角平分线的性质定理
角的平分线上的点到角的两边的距离相等.
几何语言:
∵ OC是∠AOB的平分线
PD ⊥OA, PE⊥ OB
∴ PD = PE
(角的平分线上的点到角的两边距离相等)
03
新知探究
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上
(3)垂直距离
定理的作用:
证明线段相等
03
新知探究
思考:
角的内部到角的两边距离相等的点在这个角的平分线上吗?
如图,点P在∠AOB的内部,作PD⊥OA,PE⊥OB,垂足分别在点D,E.若PD=PE.
求证:点P在∠AOB的平分线上
03
新知探究
∵ PD⊥OA,PE⊥OB,
∴ ∠PDO=∠PEO=90°.
在 Rt△PDO和 Rt△PEO中,
∵ OP=OP,PD=PE,
∴ Rt△PDO≌Rt△PEO.
∴ ∠AOC =∠BOC.
∴ OC 是∠AOB 的平分线,即点 P 在∠AOB 的平分线 OC 上.
如图 , 过点 O, P 作射线 OC.
证明:
03
新知探究
结论:
角平分线的性质逆定理
角的内部到角的两边距离相等的点在角的平分线上.
几何语言:
∵ PD⊥OA, PE⊥OB
PD = PE
∴OC是∠AOB的平分线
新课探究
例1
如图,∠BAD=∠BCD=90 °, ∠1=∠2.
(1)求证:点B在∠ABC的平分线上。
(2)求证:BD是∠ABC的角平分线。
A
B
C
D
1
2
03
新知讲解
证明(1)在△ABC中,
∵ ∠ 1=∠2
∴BA=BC
又BA ⊥AD,BC ⊥CD
∴点B在∠ABC的平分线上。
(2)在Rt△BAD和Rt△BCD中,
∵BA=BC,BD=BD
∴Rt△BAD≌Rt△BCD
∴ ∠ABD=∠CBD
∴BD是∠ABC的平分线。
04
课堂练习
【知识技能类作业】必做题:
1 .如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为 D,E,下列结论错误的是( )
A、PD=PE B、OD=OE
C、∠DPO=∠EPO D、PD=OD
2.在△ABC中,∠C=90゜,AD平分∠BAC交BC于D,BD:DC=3:2,点D到AB的距离为6,则BC长为( )
A.10 B.20 C.15 D.25
D
C
04
课堂练习
【知识技能类作业】选做题:
5、如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
求证:AC=AE
04
课堂练习
【知识技能类作业】选做题:
证明:∵在△ABC中,∠C=90°,
AD平分∠CAB,DE⊥AB,
∴CD=DE,∠AED=∠C=90°,∠CAD=∠EAD,
在△ACD和△ AED中
∴△ACD≌△AED,
∴AC=AE
04
课堂练习
【综合拓展类作业】
6.要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例1:20000)
05
课堂小结
角平分线的性质
的点
到角的两边距离相等
在角平分线上
提供了两个角相等的依据
提供了两条线段相等的依据
(性质定理)
(判定定理)
06
作业布置
【知识技能类作业】必做题:
3、如图 ,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=3,则PQ的最小值为 .
3
4、如图,AD∥BC,∠ABC的角平分 线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB 于点E.若PE=2,则两平行线AD与BC间的距离为 .
4
06
作业布置
【知识技能类作业】选做题:
已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF
证明:连接AD
在△ACD和△ABD中,
∴△ACD≌△ABD(SSS),
∴∠EAD=∠FAD,即AD平分∠EAF,
∵DE⊥AE,DF⊥AF,
∴DE=DF.
06
作业布置
【综合拓展类作业】
如图,E 是∠AOB 的平分线上一点,EC⊥OA 于点C,ED⊥OB 于点D.
求证:(1)∠ECD=∠EDC; (2)OC=OD.
证明 (1)∵ 点E在∠BOA的平分线上,
EC⊥AO,ED⊥OB ,
∴ ED =EC.
∴ △EDC 是个等腰三角形.
∴ ∠ECD=∠EDC.
06
作业布置
【综合拓展类作业】
(2)在Rt△OED和Rt△OEC中,
∵ OE= OE, ED = EC,
∴ Rt△OED≌Rt△OEC(HL).
∴ OD=OC.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
1.4.1角平分线的性质
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
在探究角平分线的性质的过程中,发展几何直觉.
提高综合运用三角形全等的有关知识解决问题的能力.
初步了解角的平分线的性质在生活、生产中的应用.
02
新知导入
角平分线的概念
一条射线
把一个角
分成两个相等的角,
这条射线叫做这个角的平分线。
o
B
C
A
1
2
03
新知探究
作法:1、以____为圆心,______长为半径作圆弧,与角的两边分别交于M、
N两点;
2、分别以_____ 为圆心,大于__________的长为半径作弧,两条圆弧交于∠AOB内一点____;
3、作射线_____;
_____就是所求作∠AOB的平分线。
点O
任意
M、N
P
OP
OP
A
B
N
M
P
O
尺规作角的平分线
03
新知探究
猜想:
角平分线的性质
折一折
03
新知探究
将AOB对折,在折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么猜想
角平分线上的点到角的两边的距离相等
03
新知探究
如图,在∠AOB的平分线OC上任取一点P,作PD⊥OA,PE⊥OB,垂足分别为点D,E,试问PD与PE相等吗?
探究
PD=PE
你能证明这个结论吗?
03
新知探究
∵ OC是∠AOB的平分线
∴ ∠DOP= ∠EOP
∵ PD ⊥OA, PE⊥ OB,
∴ ∠PDO = ∠PEO = 90°.
在△PDO 和△PEO 中,
∵ ∠PDO = ∠PEO,
∠DOP= ∠EOP,
OP= OP,
∴ △PDO≌△PEO.(AAS)
∴ PD = PE.
证明:
03
新知探究
结论:
角平分线的性质定理
角的平分线上的点到角的两边的距离相等.
几何语言:
∵ OC是∠AOB的平分线
PD ⊥OA, PE⊥ OB
∴ PD = PE
(角的平分线上的点到角的两边距离相等)
03
新知探究
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上
(3)垂直距离
定理的作用:
证明线段相等
03
新知探究
思考:
角的内部到角的两边距离相等的点在这个角的平分线上吗?
如图,点P在∠AOB的内部,作PD⊥OA,PE⊥OB,垂足分别在点D,E.若PD=PE.
求证:点P在∠AOB的平分线上
03
新知探究
∵ PD⊥OA,PE⊥OB,
∴ ∠PDO=∠PEO=90°.
在 Rt△PDO和 Rt△PEO中,
∵ OP=OP,PD=PE,
∴ Rt△PDO≌Rt△PEO.
∴ ∠AOC =∠BOC.
∴ OC 是∠AOB 的平分线,即点 P 在∠AOB 的平分线 OC 上.
如图 , 过点 O, P 作射线 OC.
证明:
03
新知探究
结论:
角平分线的性质逆定理
角的内部到角的两边距离相等的点在角的平分线上.
几何语言:
∵ PD⊥OA, PE⊥OB
PD = PE
∴OC是∠AOB的平分线
新课探究
例1
如图,∠BAD=∠BCD=90 °, ∠1=∠2.
(1)求证:点B在∠ABC的平分线上。
(2)求证:BD是∠ABC的角平分线。
A
B
C
D
1
2
03
新知讲解
证明(1)在△ABC中,
∵ ∠ 1=∠2
∴BA=BC
又BA ⊥AD,BC ⊥CD
∴点B在∠ABC的平分线上。
(2)在Rt△BAD和Rt△BCD中,
∵BA=BC,BD=BD
∴Rt△BAD≌Rt△BCD
∴ ∠ABD=∠CBD
∴BD是∠ABC的平分线。
04
课堂练习
【知识技能类作业】必做题:
1 .如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为 D,E,下列结论错误的是( )
A、PD=PE B、OD=OE
C、∠DPO=∠EPO D、PD=OD
2.在△ABC中,∠C=90゜,AD平分∠BAC交BC于D,BD:DC=3:2,点D到AB的距离为6,则BC长为( )
A.10 B.20 C.15 D.25
D
C
04
课堂练习
【知识技能类作业】选做题:
5、如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
求证:AC=AE
04
课堂练习
【知识技能类作业】选做题:
证明:∵在△ABC中,∠C=90°,
AD平分∠CAB,DE⊥AB,
∴CD=DE,∠AED=∠C=90°,∠CAD=∠EAD,
在△ACD和△ AED中
∴△ACD≌△AED,
∴AC=AE
04
课堂练习
【综合拓展类作业】
6.要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例1:20000)
05
课堂小结
角平分线的性质
的点
到角的两边距离相等
在角平分线上
提供了两个角相等的依据
提供了两条线段相等的依据
(性质定理)
(判定定理)
06
作业布置
【知识技能类作业】必做题:
3、如图 ,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=3,则PQ的最小值为 .
3
4、如图,AD∥BC,∠ABC的角平分 线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB 于点E.若PE=2,则两平行线AD与BC间的距离为 .
4
06
作业布置
【知识技能类作业】选做题:
已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF
证明:连接AD
在△ACD和△ABD中,
∴△ACD≌△ABD(SSS),
∴∠EAD=∠FAD,即AD平分∠EAF,
∵DE⊥AE,DF⊥AF,
∴DE=DF.
06
作业布置
【综合拓展类作业】
如图,E 是∠AOB 的平分线上一点,EC⊥OA 于点C,ED⊥OB 于点D.
求证:(1)∠ECD=∠EDC; (2)OC=OD.
证明 (1)∵ 点E在∠BOA的平分线上,
EC⊥AO,ED⊥OB ,
∴ ED =EC.
∴ △EDC 是个等腰三角形.
∴ ∠ECD=∠EDC.
06
作业布置
【综合拓展类作业】
(2)在Rt△OED和Rt△OEC中,
∵ OE= OE, ED = EC,
∴ Rt△OED≌Rt△OEC(HL).
∴ OD=OC.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
