第二十七章 相似 巩固训练(含答案)2024-2025学年人教版九年级下册
文档属性
| 名称 | 第二十七章 相似 巩固训练(含答案)2024-2025学年人教版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 557.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-07 07:39:04 | ||
图片预览



文档简介
第二十七章 相似 巩固训练2024-2025学年人教版九年级下册
一、单选题
1.用一个2倍放大镜照,则放大后,不发生改变的是( )
A.各内角的度数 B.各边长
C.周长 D.面积
2.如图,已知.若,,则等于( )
A.3 B.4 C.5 D.6
3.如图,在 中, , 与 , 的交点分别为 , .若 ,则 等于( )
A. B. C. D.
4.如图,在中,点,分别在边,上,且,若:=1:4,则的值为( )
A. B. C. D.
5.已知线段,,,如果线段,,,成比例,则线段d的长为( )
A.2 B.3 C.4 D.6
6.如图,在梯形中,,对角线和相交于点E,且,下列等式成立的是( ).
A. B.
C. D.
7.如图,正方形边长为4,点分别在边上,且满足交于点,分别是的中点,则的最小值为( )
A. B. C. D.
8.如图,为等腰直角三角形,于点,于点,连接,设,若,则可表示为( )
A. B. C. D.
9.如图,在矩形中,,,点是的中点,连接,平分交于点,连接交于点,则的长为( )
A. B. C. D.
10.如图,在矩形中,,,点、分别是边、的中点,某一时刻,动点从点出发,沿方向以每秒2个单位长度的速度向点匀速运动;同时,动点从点出发,沿方向以每秒1个单位长度的速度向点匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接,过点作的垂线,垂足为.在这一运动过程中,点所经过的路径长是( )
A. B. C. D.
二、填空题
11.若满足 且,则的值为 .
12.在比例尺为1:50000的地图上,量得甲、乙两地的距离为12厘米,则甲、乙两地的实际距离是 千米.
13.如图,三角形纸片中,,分别沿与平行的方向,从靠近A的AB边的三等分点剪去两个角,得到的平行四边形纸片的周长是 .
14.两个相似三角形的面积比是,其中一个三角形的周长为,则另一个三角形的周长是 .
15.如图,小亮同学跳起来把一个排球打在离他2米(即CO=2米)远的地上,排球反弹碰到墙上,如果他跳起击球时的高度是1.8米(即AC=1.8米),排球落地点离墙的距离是7米(即OD=7米),假设排球一直沿直线运动,那么排球能碰到墙面离地的高度BD的长是 米.
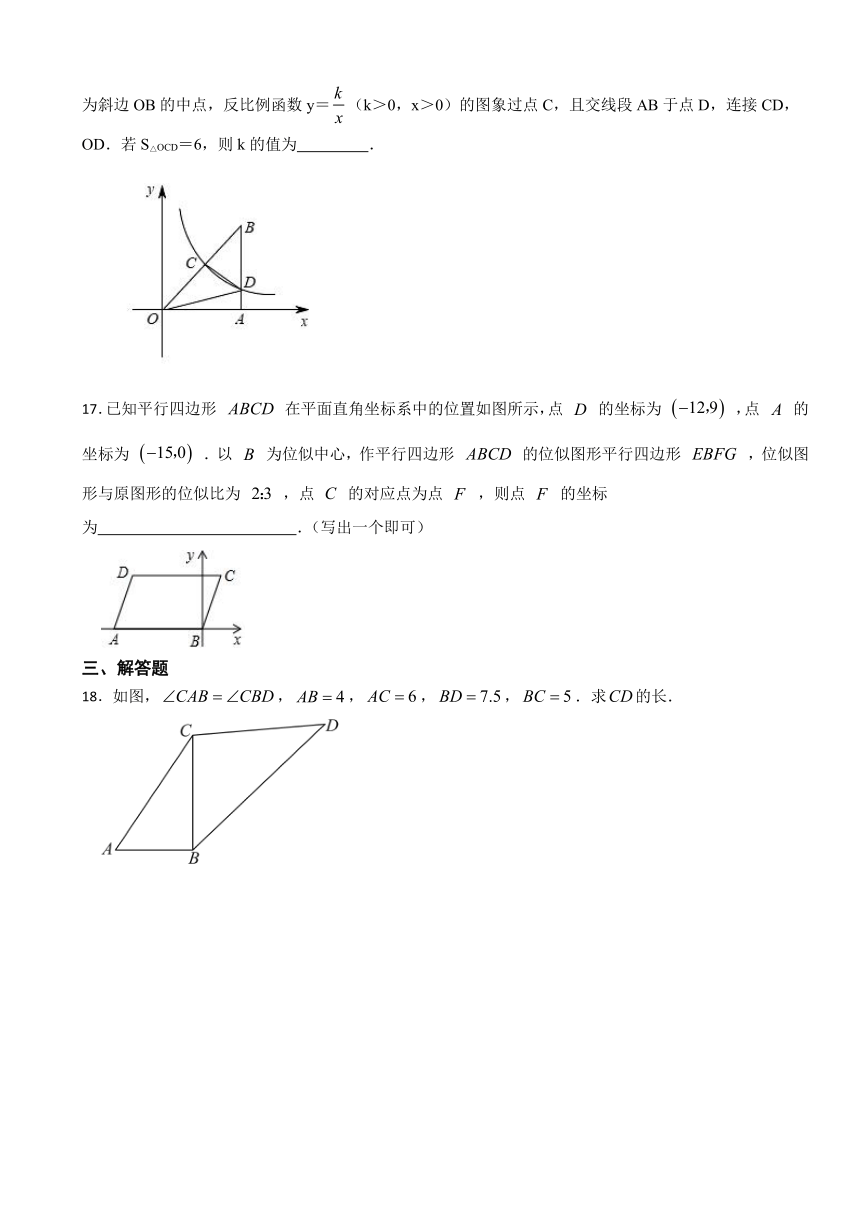
16.如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO=AB,点C为斜边OB的中点,反比例函数y=(k>0,x>0)的图象过点C,且交线段AB于点D,连接CD,OD.若S△OCD=6,则k的值为 .
17.已知平行四边形 在平面直角坐标系中的位置如图所示,点 的坐标为 ,点 的坐标为 .以 为位似中心,作平行四边形 的位似图形平行四边形 ,位似图形与原图形的位似比为 ,点 的对应点为点 ,则点 的坐标为 .(写出一个即可)
三、解答题
18.如图,,,,,.求的长.
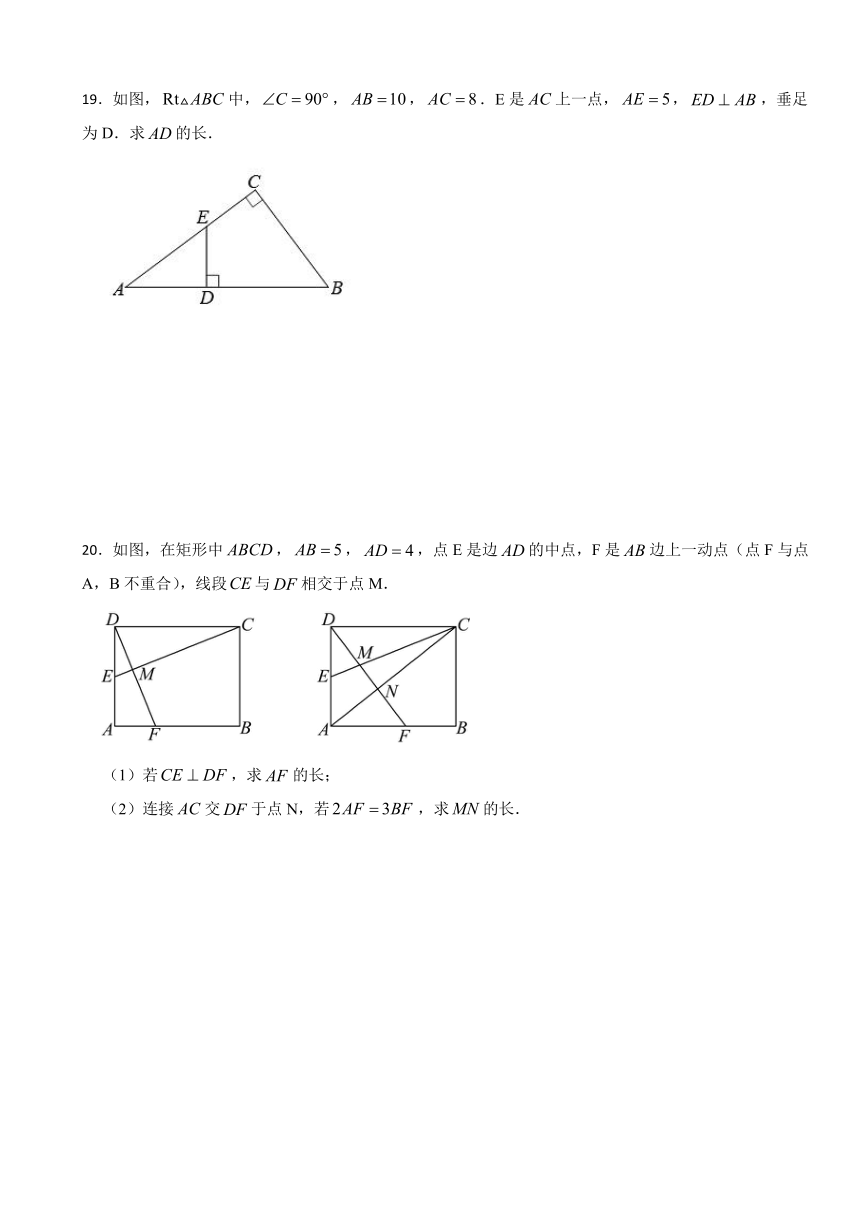
19.如图,中,,,.E是上一点,,,垂足为D.求的长.
20.如图,在矩形中,,,点E是边的中点,F是边上一动点(点F与点A,B不重合),线段与相交于点M.
(1)若,求的长;
(2)连接交于点N,若,求的长.
21.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件PQMN,使一边在BC上,其余两个顶点分别在边AB、AC上.若这个矩形的边PN∶PQ=1∶2,则这个矩形的长、宽各是多少?
22.为了加快城市发展,保障市民出行方便,在流经该市的河流上架起一座桥,连通南北,铺就城市繁荣之路.小明和小颖想通过自己所学的数学知识计算该桥AF的长.如图,该桥两侧河岸平行他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在AB,AC的延长线上取点D,E,使得 DE∥BC .经测量BC=80米,DE=140米,且点E到河岸BC的距离为90米,已知AF⊥BC于点F,请你根据提供的数据,帮助他们计算桥AF的长度
23.如图,在中,,,,点为边上的动点,点从点出发,沿边往运动,当运动到点时停止,若设点运动的时间为秒,点运动的速度为每秒2个单位长度.
(1)当时, , ;(请直接写出答案)
(2)当为何值时,是直角三角形;(写出解答过程)
(3)求当为何值时,是等腰三角形?并说明理由.
答案部分
1.A
2.D
3.B
4.B
5.D
6.C
7.C
8.C
9.B
10.A
11.
12.
13.14
14.或
15.6.3
16.8
17.(-2,-6)或(2,6)
18.
19.4
20.(1).
(2).
21.解:∵PQMN是矩形,
∴PQ∥BC,
∴△APQ∽△ABC,
设边PN为xmm,则PQ为2xmm,
即
∵AD是高,
∴PN∥AD,
∴△PBN∽△ABD,
∴
即 ,
∵AP+BP=AB,
∴ =1,
解得x= ,2x= .
即长为 mm,宽为 mm.
答:矩形的长为 mm,宽是 mm.
22.解:
如图所示,过E作 于G,
∵AF⊥BC, EG⊥BC,
∴∠EGC=∠AFC=90°,
又∵∠ACF=∠GCE,
∴△ACF∽△ECG,
即:
解得AF=120,
∴桥AF的长度为120米.
23.(1)4;21
(2)解:①∠CDB=90°时,AC BDAB BC,
∴BD,
所以CD=,
∴,
解得:(秒);
②∠CBD=90°时,点D和点A重合,
∴,
解得:(秒);
综上所述,当或秒时,△CBD是直角三角形;
(3)解:①CD=BD时,如图1,过点D作DE⊥BC于E,
则CE=BE,DE∥AB,
∴CD=AD=AC=,
∴,
解得:(秒);
②CD=BC时,CD=15,
∴,
解得:(秒);
③BD=BC时,如图2,过点B作BF⊥AC于F,
∵S△BCA=AB×BC=AC×BF,
∴×20×15=×25BF,
∴BF=12,
在△BCF中,
∵BC=BD,BF⊥AC,
∴CD=2CF=18,
∴,
解得:(秒);
综上所述,当或或秒时,△CBD是等腰三角形.
一、单选题
1.用一个2倍放大镜照,则放大后,不发生改变的是( )
A.各内角的度数 B.各边长
C.周长 D.面积
2.如图,已知.若,,则等于( )
A.3 B.4 C.5 D.6
3.如图,在 中, , 与 , 的交点分别为 , .若 ,则 等于( )
A. B. C. D.
4.如图,在中,点,分别在边,上,且,若:=1:4,则的值为( )
A. B. C. D.
5.已知线段,,,如果线段,,,成比例,则线段d的长为( )
A.2 B.3 C.4 D.6
6.如图,在梯形中,,对角线和相交于点E,且,下列等式成立的是( ).
A. B.
C. D.
7.如图,正方形边长为4,点分别在边上,且满足交于点,分别是的中点,则的最小值为( )
A. B. C. D.
8.如图,为等腰直角三角形,于点,于点,连接,设,若,则可表示为( )
A. B. C. D.
9.如图,在矩形中,,,点是的中点,连接,平分交于点,连接交于点,则的长为( )
A. B. C. D.
10.如图,在矩形中,,,点、分别是边、的中点,某一时刻,动点从点出发,沿方向以每秒2个单位长度的速度向点匀速运动;同时,动点从点出发,沿方向以每秒1个单位长度的速度向点匀速运动,其中一点运动到矩形顶点时,两点同时停止运动,连接,过点作的垂线,垂足为.在这一运动过程中,点所经过的路径长是( )
A. B. C. D.
二、填空题
11.若满足 且,则的值为 .
12.在比例尺为1:50000的地图上,量得甲、乙两地的距离为12厘米,则甲、乙两地的实际距离是 千米.
13.如图,三角形纸片中,,分别沿与平行的方向,从靠近A的AB边的三等分点剪去两个角,得到的平行四边形纸片的周长是 .
14.两个相似三角形的面积比是,其中一个三角形的周长为,则另一个三角形的周长是 .
15.如图,小亮同学跳起来把一个排球打在离他2米(即CO=2米)远的地上,排球反弹碰到墙上,如果他跳起击球时的高度是1.8米(即AC=1.8米),排球落地点离墙的距离是7米(即OD=7米),假设排球一直沿直线运动,那么排球能碰到墙面离地的高度BD的长是 米.
16.如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO=AB,点C为斜边OB的中点,反比例函数y=(k>0,x>0)的图象过点C,且交线段AB于点D,连接CD,OD.若S△OCD=6,则k的值为 .
17.已知平行四边形 在平面直角坐标系中的位置如图所示,点 的坐标为 ,点 的坐标为 .以 为位似中心,作平行四边形 的位似图形平行四边形 ,位似图形与原图形的位似比为 ,点 的对应点为点 ,则点 的坐标为 .(写出一个即可)
三、解答题
18.如图,,,,,.求的长.
19.如图,中,,,.E是上一点,,,垂足为D.求的长.
20.如图,在矩形中,,,点E是边的中点,F是边上一动点(点F与点A,B不重合),线段与相交于点M.
(1)若,求的长;
(2)连接交于点N,若,求的长.
21.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件PQMN,使一边在BC上,其余两个顶点分别在边AB、AC上.若这个矩形的边PN∶PQ=1∶2,则这个矩形的长、宽各是多少?
22.为了加快城市发展,保障市民出行方便,在流经该市的河流上架起一座桥,连通南北,铺就城市繁荣之路.小明和小颖想通过自己所学的数学知识计算该桥AF的长.如图,该桥两侧河岸平行他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在AB,AC的延长线上取点D,E,使得 DE∥BC .经测量BC=80米,DE=140米,且点E到河岸BC的距离为90米,已知AF⊥BC于点F,请你根据提供的数据,帮助他们计算桥AF的长度
23.如图,在中,,,,点为边上的动点,点从点出发,沿边往运动,当运动到点时停止,若设点运动的时间为秒,点运动的速度为每秒2个单位长度.
(1)当时, , ;(请直接写出答案)
(2)当为何值时,是直角三角形;(写出解答过程)
(3)求当为何值时,是等腰三角形?并说明理由.
答案部分
1.A
2.D
3.B
4.B
5.D
6.C
7.C
8.C
9.B
10.A
11.
12.
13.14
14.或
15.6.3
16.8
17.(-2,-6)或(2,6)
18.
19.4
20.(1).
(2).
21.解:∵PQMN是矩形,
∴PQ∥BC,
∴△APQ∽△ABC,
设边PN为xmm,则PQ为2xmm,
即
∵AD是高,
∴PN∥AD,
∴△PBN∽△ABD,
∴
即 ,
∵AP+BP=AB,
∴ =1,
解得x= ,2x= .
即长为 mm,宽为 mm.
答:矩形的长为 mm,宽是 mm.
22.解:
如图所示,过E作 于G,
∵AF⊥BC, EG⊥BC,
∴∠EGC=∠AFC=90°,
又∵∠ACF=∠GCE,
∴△ACF∽△ECG,
即:
解得AF=120,
∴桥AF的长度为120米.
23.(1)4;21
(2)解:①∠CDB=90°时,AC BDAB BC,
∴BD,
所以CD=,
∴,
解得:(秒);
②∠CBD=90°时,点D和点A重合,
∴,
解得:(秒);
综上所述,当或秒时,△CBD是直角三角形;
(3)解:①CD=BD时,如图1,过点D作DE⊥BC于E,
则CE=BE,DE∥AB,
∴CD=AD=AC=,
∴,
解得:(秒);
②CD=BC时,CD=15,
∴,
解得:(秒);
③BD=BC时,如图2,过点B作BF⊥AC于F,
∵S△BCA=AB×BC=AC×BF,
∴×20×15=×25BF,
∴BF=12,
在△BCF中,
∵BC=BD,BF⊥AC,
∴CD=2CF=18,
∴,
解得:(秒);
综上所述,当或或秒时,△CBD是等腰三角形.
