第二十六章 反比例函数 巩固训练(含答案)2024-2025学年人教版九年级下册
文档属性
| 名称 | 第二十六章 反比例函数 巩固训练(含答案)2024-2025学年人教版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 460.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-07 07:43:04 | ||
图片预览


文档简介
第二十六章 反比例函数 巩固训练2024-2025学年人教版九年级下册
一、单选题
1.已知反比例函数的图象经过点,那么下列四个点中,也在这个函数图象上的是( )
A. B. C. D.
2.若反比例函数的图象经过点(﹣1,4),则它的函数表达式是( )
A.y B.y C.y D.y
3.反比例函数y= 的图象与直线y=﹣x+2有两个交点,且两交点横坐标的积为负数,则t的取值范围是( )
A.t< B.t> C.t≤ D.t≥
4.已知反比例函数y= ,给出下列结论:①该函数图象在一、三象限;②若x>3,则0n>p。其中正确的是( )
A.①② B.②③ C.①③ D.①②③
5.已知函数y=,下列说法:①函数图象分布在第一、三象限;②在每个象限内,y随x的增大而减小;③若A(x1,y1) ,B(x2,y2)两点在该函数图象上,且x1+x2=0,则y1 =y2,其中说法正确的个数是( )
A.0 B.1 C.2 D.3
6.如图,四边形OABC和四边形BDEF都是正方形,反比例函数在第一象限的图像经过点E,若两正方形的面积差为12,则k的值为( )
A.12 B.6 C.10 D.8
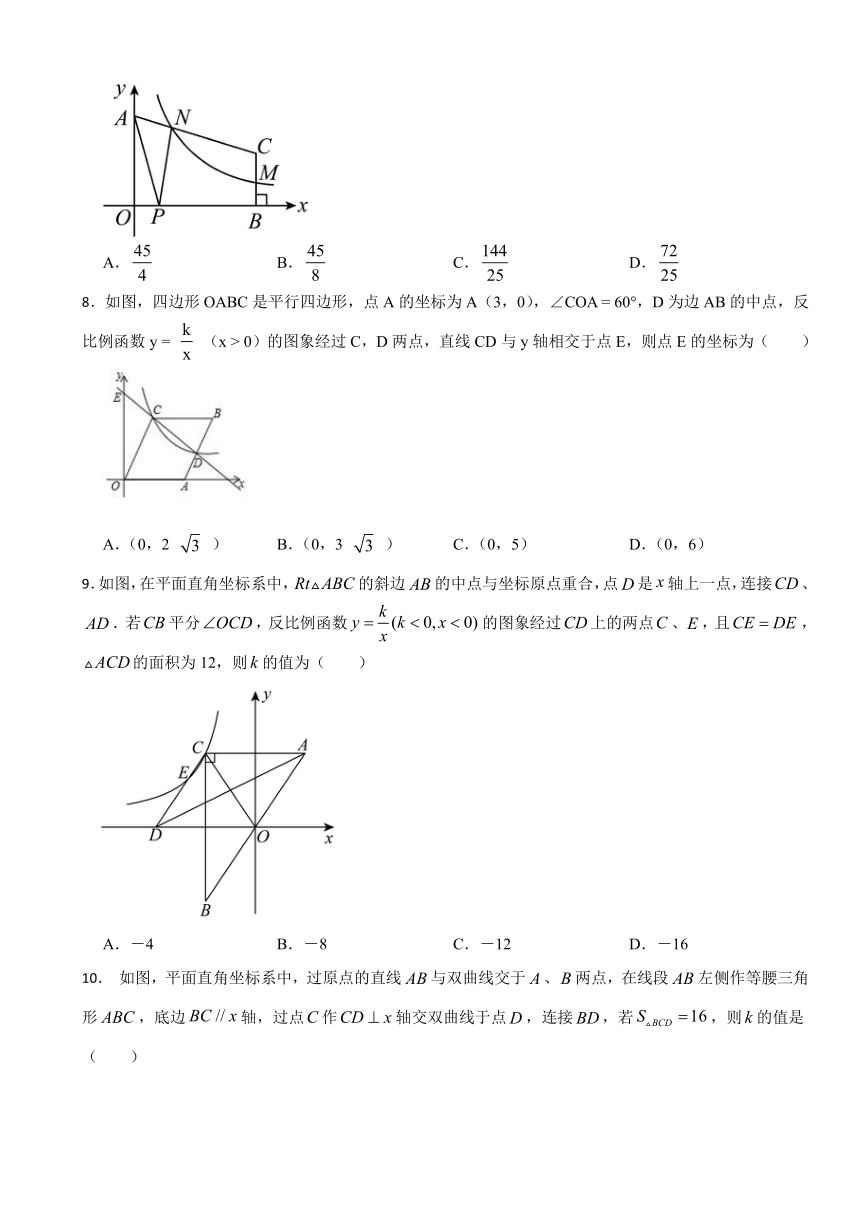
7.如图,在平面直角坐标系中,点A、B分别在y,x轴上,轴.点M、N分别在线段、上,,,反比例函数的图象经过M、N两点,P为x正半轴上一点,且,的面积为3,则k的值为( )
A. B. C. D.
8.如图,四边形OABC是平行四边形,点A的坐标为A(3,0),∠COA = 60°,D为边AB的中点,反比例函数y = (x > 0)的图象经过C,D两点,直线CD与y轴相交于点E,则点E的坐标为( )
A.(0,2 ) B.(0,3 ) C.(0,5) D.(0,6)
9.如图,在平面直角坐标系中,的斜边的中点与坐标原点重合,点是轴上一点,连接、.若平分,反比例函数的图象经过上的两点、,且,的面积为12,则的值为( )
A.-4 B.-8 C.-12 D.-16
10. 如图,平面直角坐标系中,过原点的直线与双曲线交于、两点,在线段左侧作等腰三角形,底边轴,过点作轴交双曲线于点,连接,若,则的值是( )
A. B. C. D.
二、填空题
11.如图,A,B是双曲线上的两点,过点A作轴于点,交于点,且为的中点,若的面积为5,点B的坐标为,则的值为 .
12.已知点与点均在反比例函数的图象上,则的值是 .
13.某反比例函数图象如图所示,已知点A在该图象上,过点A作AC⊥y轴于与点C,B为x轴上一点,连接和,若,求该反比例函数的表达式.
14.反比例函数,当时,函数的最大值和最小值之差为4,则 .
15. 在平面直角坐标系中,若函数的图像经过点和,则m的值为 .
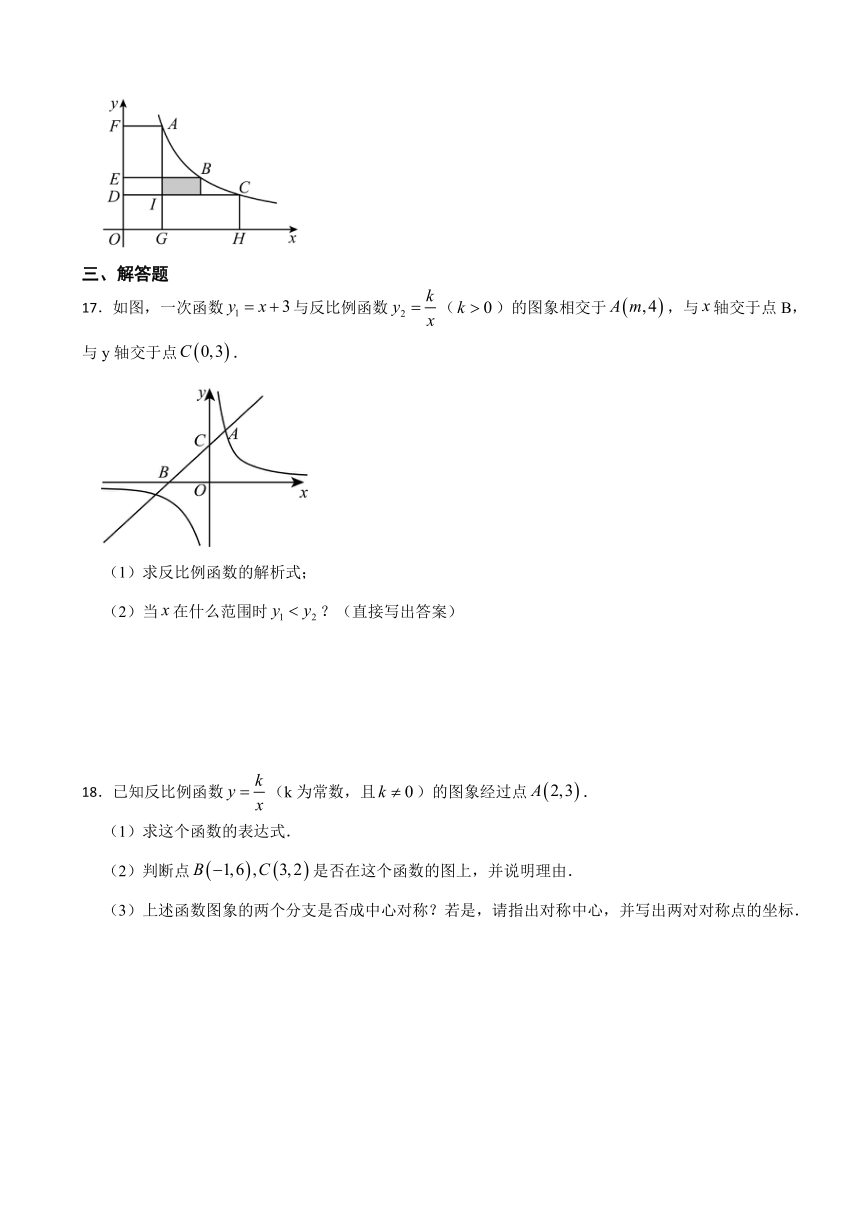
16.如图,点A,B,C在函数(常数,)图象上的位置如图所示,分别过点A,C作x轴与y轴的垂线,过点B作y轴与的垂线.若,图中所构成的阴影部分面积为2,则矩形的面积为 .
三、解答题
17.如图,一次函数与反比例函数()的图象相交于,与轴交于点B,与y轴交于点.
(1)求反比例函数的解析式;
(2)当在什么范围时?(直接写出答案)
18.已知反比例函数(k为常数,且)的图象经过点.
(1)求这个函数的表达式.
(2)判断点是否在这个函数的图上,并说明理由.
(3)上述函数图象的两个分支是否成中心对称?若是,请指出对称中心,并写出两对对称点的坐标.
19.已知某蓄电池的电压为定值,使用该蓄电池时,电流单位:与电阻单位:是反比例函数关系,它的图象如图所示.
(1)求出这个反比例函数的解析式;
(2)如果以此蓄电池为电源的用电器限制电流不能超过,求出用电器可变电阻应控制在什么范围.
20.已知一个一次函数的图象与一个反比例函的图象交于点、.
(1)分别求出这两个函数的表达式.
(2)直接写出当x取何值时,一次函数的值大于反比例函数的值.
21.如图,一次函数的图像与反比例函数在第一象限的图像交于和两点,与x轴交于点C,
(1)求反比例函数的关系式;
(2)根据图像,当时x的取值范围为:______;
(3)若点P在x轴上,且,求点P的坐标;
(4)若点P在y轴上,Q在双曲线上,当以A、B、P、Q为顶点的四边形是平行四边形时,直接写出Q点的坐标:______.
22.我们称关于的二次函数为一次函数和反比例函数的“共同体”函数.一次函数和反比例函数的交点称为二次函数的“共赢点”.
(1)一次函数和反比例函数的“共同体”函数是 ,它的“共赢点”为 ;
(2)已知二次函数与轴的交点为、,有、两个“共赢点”,且,求的值;
(3)若一次函数和反比例函数的“共同体”函数的两个“共赢点”的横坐标为,其中实数,.令,求的取值范围.
答案部分
1.C
2.A
3.B
4.D
5.B
6.A
7.B
8.B
9.B
10.B
11.10
12.0
13.
14.-6
15.1
16.
17.(1)
(2) 或
18.(1)
(2)点B不在这个函数的图象上,点C在这个函数的图象上
(3)成中心对称,对称中心是原点,两对对称点坐标为和,和
19.(1)解:电流是电阻的反比例函数,设,
图象经过,
,
解得:,
这个反比例函数的解析式为;
(2)解:,,
,
,
即用电器可变电阻应控制在欧以上的范围内.
20.(1)解:设反比例函数解析式为
将代入得,
解得
∴反比例函数解析式为;
将代入,得
∴
设一次函数解析式为
将,代入得
解得
∴;
(2)解:或
21.(1)
(2)或
(3)或
(4)或
22.(1);,
(2)±
(3)
一、单选题
1.已知反比例函数的图象经过点,那么下列四个点中,也在这个函数图象上的是( )
A. B. C. D.
2.若反比例函数的图象经过点(﹣1,4),则它的函数表达式是( )
A.y B.y C.y D.y
3.反比例函数y= 的图象与直线y=﹣x+2有两个交点,且两交点横坐标的积为负数,则t的取值范围是( )
A.t< B.t> C.t≤ D.t≥
4.已知反比例函数y= ,给出下列结论:①该函数图象在一、三象限;②若x>3,则0
A.①② B.②③ C.①③ D.①②③
5.已知函数y=,下列说法:①函数图象分布在第一、三象限;②在每个象限内,y随x的增大而减小;③若A(x1,y1) ,B(x2,y2)两点在该函数图象上,且x1+x2=0,则y1 =y2,其中说法正确的个数是( )
A.0 B.1 C.2 D.3
6.如图,四边形OABC和四边形BDEF都是正方形,反比例函数在第一象限的图像经过点E,若两正方形的面积差为12,则k的值为( )
A.12 B.6 C.10 D.8
7.如图,在平面直角坐标系中,点A、B分别在y,x轴上,轴.点M、N分别在线段、上,,,反比例函数的图象经过M、N两点,P为x正半轴上一点,且,的面积为3,则k的值为( )
A. B. C. D.
8.如图,四边形OABC是平行四边形,点A的坐标为A(3,0),∠COA = 60°,D为边AB的中点,反比例函数y = (x > 0)的图象经过C,D两点,直线CD与y轴相交于点E,则点E的坐标为( )
A.(0,2 ) B.(0,3 ) C.(0,5) D.(0,6)
9.如图,在平面直角坐标系中,的斜边的中点与坐标原点重合,点是轴上一点,连接、.若平分,反比例函数的图象经过上的两点、,且,的面积为12,则的值为( )
A.-4 B.-8 C.-12 D.-16
10. 如图,平面直角坐标系中,过原点的直线与双曲线交于、两点,在线段左侧作等腰三角形,底边轴,过点作轴交双曲线于点,连接,若,则的值是( )
A. B. C. D.
二、填空题
11.如图,A,B是双曲线上的两点,过点A作轴于点,交于点,且为的中点,若的面积为5,点B的坐标为,则的值为 .
12.已知点与点均在反比例函数的图象上,则的值是 .
13.某反比例函数图象如图所示,已知点A在该图象上,过点A作AC⊥y轴于与点C,B为x轴上一点,连接和,若,求该反比例函数的表达式.
14.反比例函数,当时,函数的最大值和最小值之差为4,则 .
15. 在平面直角坐标系中,若函数的图像经过点和,则m的值为 .
16.如图,点A,B,C在函数(常数,)图象上的位置如图所示,分别过点A,C作x轴与y轴的垂线,过点B作y轴与的垂线.若,图中所构成的阴影部分面积为2,则矩形的面积为 .
三、解答题
17.如图,一次函数与反比例函数()的图象相交于,与轴交于点B,与y轴交于点.
(1)求反比例函数的解析式;
(2)当在什么范围时?(直接写出答案)
18.已知反比例函数(k为常数,且)的图象经过点.
(1)求这个函数的表达式.
(2)判断点是否在这个函数的图上,并说明理由.
(3)上述函数图象的两个分支是否成中心对称?若是,请指出对称中心,并写出两对对称点的坐标.
19.已知某蓄电池的电压为定值,使用该蓄电池时,电流单位:与电阻单位:是反比例函数关系,它的图象如图所示.
(1)求出这个反比例函数的解析式;
(2)如果以此蓄电池为电源的用电器限制电流不能超过,求出用电器可变电阻应控制在什么范围.
20.已知一个一次函数的图象与一个反比例函的图象交于点、.
(1)分别求出这两个函数的表达式.
(2)直接写出当x取何值时,一次函数的值大于反比例函数的值.
21.如图,一次函数的图像与反比例函数在第一象限的图像交于和两点,与x轴交于点C,
(1)求反比例函数的关系式;
(2)根据图像,当时x的取值范围为:______;
(3)若点P在x轴上,且,求点P的坐标;
(4)若点P在y轴上,Q在双曲线上,当以A、B、P、Q为顶点的四边形是平行四边形时,直接写出Q点的坐标:______.
22.我们称关于的二次函数为一次函数和反比例函数的“共同体”函数.一次函数和反比例函数的交点称为二次函数的“共赢点”.
(1)一次函数和反比例函数的“共同体”函数是 ,它的“共赢点”为 ;
(2)已知二次函数与轴的交点为、,有、两个“共赢点”,且,求的值;
(3)若一次函数和反比例函数的“共同体”函数的两个“共赢点”的横坐标为,其中实数,.令,求的取值范围.
答案部分
1.C
2.A
3.B
4.D
5.B
6.A
7.B
8.B
9.B
10.B
11.10
12.0
13.
14.-6
15.1
16.
17.(1)
(2) 或
18.(1)
(2)点B不在这个函数的图象上,点C在这个函数的图象上
(3)成中心对称,对称中心是原点,两对对称点坐标为和,和
19.(1)解:电流是电阻的反比例函数,设,
图象经过,
,
解得:,
这个反比例函数的解析式为;
(2)解:,,
,
,
即用电器可变电阻应控制在欧以上的范围内.
20.(1)解:设反比例函数解析式为
将代入得,
解得
∴反比例函数解析式为;
将代入,得
∴
设一次函数解析式为
将,代入得
解得
∴;
(2)解:或
21.(1)
(2)或
(3)或
(4)或
22.(1);,
(2)±
(3)
