1.4.2角平分线的性质 教案

中小学教育资源及组卷应用平台
分课时教学设计
第8课时《1.4.2角平分线的性质》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 经历对角的平分线的性质的探索与形成的过程。发展应用数学知识的意识与能力，培养学生的联想、探索、概括归纳的能力，激发学生学习数学的兴趣.
学习者分析 通过让学生经历动手实践，合作交流，演绎推理的过程，使学生学会理性思考，从而提高解决简单问题的能力.
教学目标 角平分线的性质及其应用． 2.能应用角平分线的两个性质解决一些简单的实际问题．
教学重点 角平分线的性质及其应用．
教学难点 灵活应用两个性质解决问题.
学习活动设计
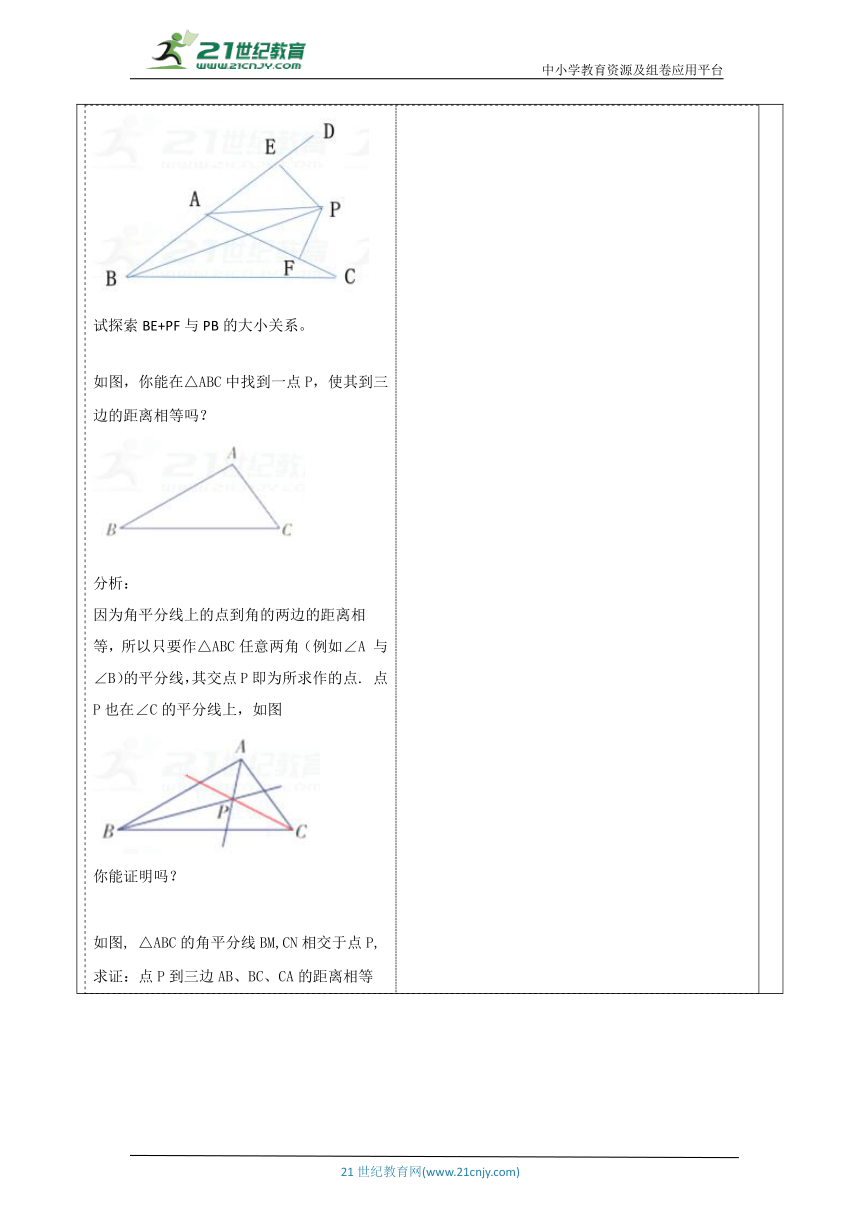
教师活动学生活动环节一：引入新课复习引入 1、角的平分线的性质定理: 几何语言表述： 2、角平分线的性质定理的逆定理： 学生活动1： 学生在教师的引导下，能很快回忆相关问题. ? 活动意图说明：激发学生兴趣,引入新课主题，激发学生的兴趣，理解学生思考，进行探索. 环节二：新知探究教师活动2： 动脑筋： 如图，已知 EF⊥CD，EF⊥AB，MN⊥AC，M 是 EF 的中点. 需添加一个什么条件，就可使 CM，AM分别为∠ACD和∠CAB的平分线呢？ 学生活动2： 学生自学、互动。在具体计算时，可以通过小组合作交流，放手让学生去思考、讨论，猜想、发现结论． 学生自主解答，教师适时的进行提示 学生思考 活动意图说明：从旧知识出发，呼应引课问题，学生通过自己解决问题，让学生在小组内共同合作．教师要有足够的耐心，要为学生的思考留有时间和空间. 环节三：典例精析 例2、如图，在△ABC的外角∠DAC的平分线上任取一点P，作PE⊥DB，PF⊥AC，垂足分别为点E，F。 试探索BE+PF与PB的大小关系。 如图，你能在△ABC中找到一点P，使其到三边的距离相等吗？ 分析： 因为角平分线上的点到角的两边的距离相等，所以只要作△ABC任意两角（例如∠A 与∠B）的平分线，其交点P即为所求作的点. 点P也在∠C的平分线上，如图 你能证明吗？ 如图, △ABC的角平分线BM,CN相交于点P, 求证：点P到三边AB、BC、CA的距离相等 归纳： 定理：三角形的三条角平分线相较于一点，并且这一点到三边的距离相等。 这个交点叫做三角形的内心 学生活动3： 参与教师分析和讲例题． 在学生自主、合作、探究后，学生解答，师生归纳出 让学生试着寻找解题思路；教师可引导学生发现证明的思路 活动意图说明：熟练掌握.巩固学的知识，学生通过自己解决问题，充分发挥学习的主动性，通过此题的解答，培养学生动手操作能力和寻求解决数学问题的一般方法.?
板书设计
课堂练习 【知识技能类作业】 必做题： 1 .到三角形三边距离相等的点是（ ） A.三条高的交点 B. 三条中线的交点 C. 三条角平分线的交点 D. 不能确定 2.如图所示，△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于D，DE⊥AB于E，且AB＝6cm，则△DEB的周长为（ ） A.4cm B.6cm C.10cm D. 以上都不对 选做题： 3、某市有一块有三条公路围成的三角形绿地，现准备在绿地中建一小亭供人小憩，使小亭中心到三条公路的距离相等，试确定小亭的中心位置． 要求：在给出的示意图上用直尺和圆规作出小亭中心位置（用P表示），不写作法，但要保留作图痕迹． 【综合拓展类作业】 4、如图，在△ABC中，AD平分∠BAC中，AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，求证：AD⊥EF．　　
课堂总结
作业设计 【知识技能类作业】 必做题： 1、如图，△ABC的∠ABC的外角平分线BD与∠ACB的外角平分线CE相交于点P，若点P到AC的距离为4，则点P到AB的距离为　 . 2、如图，点M在∠ABC内，ME⊥AB于E点，MF⊥BC于F点，且ME=MF，∠ABC=70°，则∠BME=　 °． 选做题： 3.如图，为了促进当地旅游发展，某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建 【综合拓展类作业】 4.如图：△ABC中，AD是∠BAC的平分线，E、F分别为AB、AC上的点，且∠EDF＋∠BAF＝180°． 求证：DE＝DF
教学反思 1、角的平分线的性质定理: 角的平分线上的点到角的两边的距离相等 2、角平分线的性质定理的逆定理： 角的内部到角的两边距离相等的点在角的平分线上。 3.角平分线的性质定理和角平分线的判定定理是证明角相等、线段相等的新途径
21世纪教育网(www.21cnjy.com)