2024-2025学年上学期人教版八年级数学期末综合测试题(含答案)
文档属性
| 名称 | 2024-2025学年上学期人教版八年级数学期末综合测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 736.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-06 22:39:17 | ||
图片预览




文档简介
人教版八年级数学上册综合测试题
测试时间:100分钟,总分:120分
一.选择题(共10小题,满分30分,每小题3分)
1.下列四个图形中,其中不是轴对称图形的是( )
A. B. C. D.
2.纳米科技是新兴科技,1纳米=0.000000001米,则5纳米用科学记数法表示为( )
A.5×10﹣8米 B.5×10﹣9米 C.5×10﹣10米 D.5×109米
3.下列计算正确的是( )
A.(a2)3=a6 B.a2a3=a C.(2a)3=2a3 D.a10÷a2=a5
4.如图,△ABC中,AB=AC,BD=CE,BF=CD,若∠A=50°,则∠EDF的度数是( )
A.75° B.70° C.65° D.60°
(4题图) (5题图)
5.如图,小陈从O点出发,前进5米后向右转20°,再前进5米后又向右转20°,…,这样一直走下去,他第一次回到出发点O时一共走了( )
A.60米 B.100米 C.90米
6.化简的结果是( )
A.a+a2 B.a﹣1 C.a+1 D.1
7.“五一”前夕,某校社团进行爱心义卖活动,先用800元购进第一批康乃馨,包装后售完,接着又用400元购进第二批康乃馨,已知第二批所购数量是第一批所购数量的,且康乃馨的单价比第一批的单价多1元,设第一批康乃馨的单价是x元,则下列方程正确的是( )
A. B.
C.1 D.1
8.已知点P(a,3)和点Q(4,b)关于x轴对称,则(a+b)2021的值为( )
A.1 B.﹣1 C.72021 D.﹣72021
9.如图,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟是1m,Q点从B向D运动,每分钟走2m,当P、Q两点同时出发t分钟后△CAP全等于△PBQ,则此时t的值是( )
A.4 B.6 C.8 D.10
10.下列条件能判定△ABC为等腰三角形的是( )
A.∠A=30°,∠B=60° B.AB=5,AC=12,BC=13
C.∠A=50°,∠B=80° D.∠A:∠B:∠C=3:4:5
二.填空题(共5小题,满分15分,每小题3分)
11.如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若DC=6,则点D到直线AB的距离= .
12.若分式有意义,则a的取值范围是 .
13.设矩形的两条邻边长分别为x,y,且满足y,若此矩形能被分割成3个全等的正方形,则这个矩形的对角线长是 .
14.分解因式:x2﹣7x﹣30= .
15.如图,在△ABC中,∠B=42°,点D,E分别是BA,BC边上的点,将△BDE沿DE所在直线对折,得到△FDE.若∠ADF=134°,则
∠CEF的度数为 .
三.解答题(共8小题,满分75分)
16.(8分)分解因式:
(1)a3﹣4ab2; (2)3ma2﹣18ma+27m.
17.(12分)计算:
(1)3a3b (﹣2ab)+(﹣3a2b)2; (2)(x+y)2﹣(y+2x)(y﹣2x);
(3)(2ab2c﹣3)﹣2÷(a﹣2b)3; (4).
18.(8分)(1)解方程:;
(2)先化简:,当a为整数时,该代数式的值也为整数,请直接写出所有a值.
19.(8分)如图,∠B=∠C,AD=AE,∠1=∠2.求证:∠M=∠N.
20.(9分)如图,在Rt△ABC中,∠BAC=90°,D是BC边上一点,且BD=BA.
(1)尺规作图:作∠ABC的角平分线交AD于点E,作线段DC的中点F;(保留作图痕迹,不写作法)
(2)连接EF,若∠EBD=20°,求∠BEF的度数.
21.(9分)“”称为二阶行列式,规定它的运算法则为:,例如:.
(1)计算;
(2)求等式中x的值.
22.(10分)【阅读材料】
我们知道,图形也是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙地解决一些图形问题.
在一次数学活动课上,张老师准备了若干张如图1所示的甲、乙、丙三种纸片,其中甲种纸片是边长为x的正方形,乙种纸片是边长为y的正方形,丙种纸片是长为y,宽为x的长方形,并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
【理解应用】
(1)观察图2,请用两种不同方式计算阴影部分的面积,并把得到的等式写出来.
【拓展升华】
(2)利用(1)中的等式解决下列问题.
已知a2+b2=10,a+b=6,求ab的值;
(3)若用图一中的卡片拼成一个边长为y+3x的正方形,则需要甲型卡片 张、乙型卡片 张、丙型卡片 张.
23.(11分)【课本再现】
本学期同学们在学习第十三章《轴对称》,第三单元13.3等腰三角形,第二课13.3.2等边三角形时(P81),学习了一个定理.
定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
【定理探索】
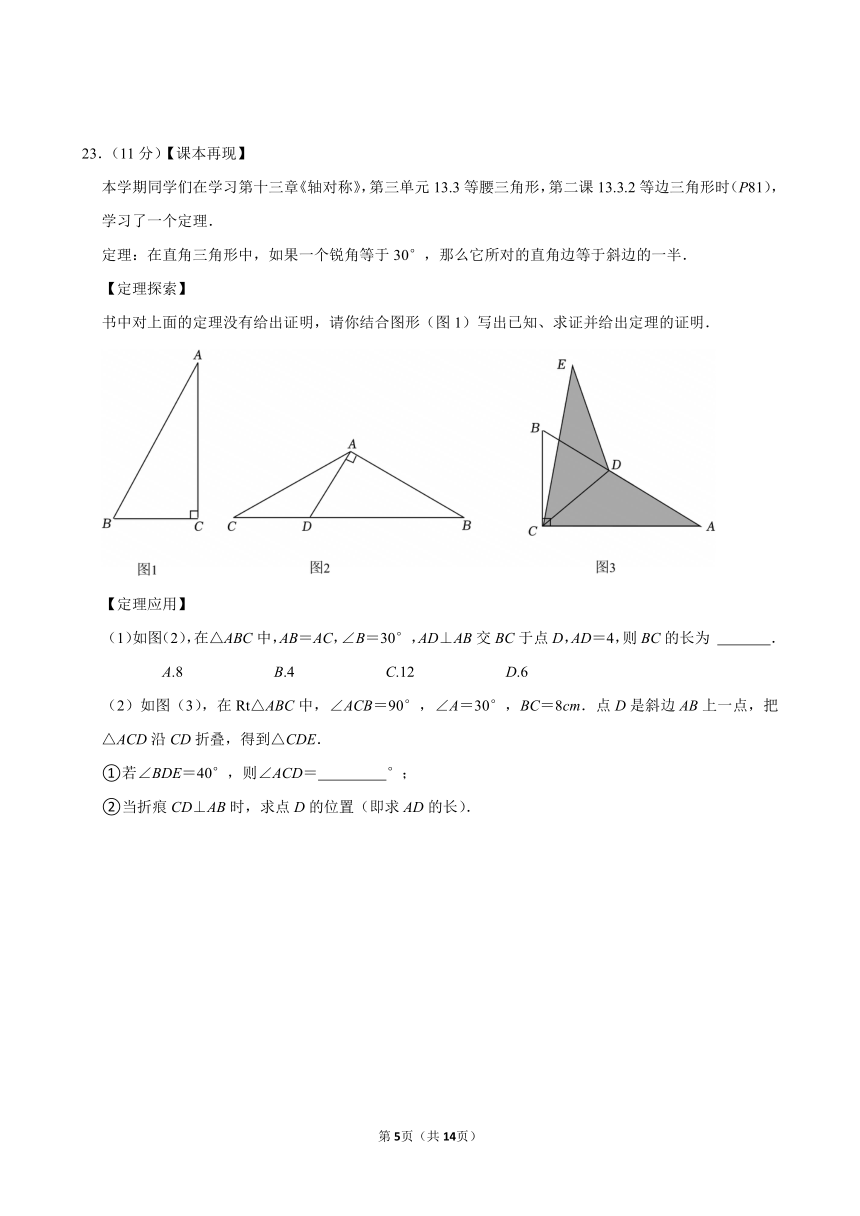
书中对上面的定理没有给出证明,请你结合图形(图1)写出已知、求证并给出定理的证明.
【定理应用】
(1)如图(2),在△ABC中,AB=AC,∠B=30°,AD⊥AB交BC于点D,AD=4,则BC的长为 .
A.8 B.4 C.12 D.6
(2)如图(3),在Rt△ABC中,∠ACB=90°,∠A=30°,BC=8cm.点D是斜边AB上一点,把△ACD沿CD折叠,得到△CDE.
①若∠BDE=40°,则∠ACD= °;
②当折痕CD⊥AB时,求点D的位置(即求AD的长).
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:选项A、C、D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选:B.
2.解:5纳米=0.000000005米=5×10﹣9米.
选:B.
3.解:A.(a2)3=a6,本选项符合题意;
B.a2a3=a5,本选项不符合题意;
C.(2a)3=8a3,本选项不符合题意;
D.a10÷a2=a8,本选项不符合题意.
选:A.
4.解:∵AB=AC、∠A=50°,
∴∠B=∠C(180°﹣∠A)=65°.
在△BDF和△CED中,,
∴△BDF≌△CED(SAS),
∴∠CDE=∠BFD.
∵∠BDF+∠BFD+∠B=180°,∠BDF+∠EDF+∠CDE=180°,
∴∠EDF=∠B=65°.
选:C.
5.解:依题意可知,小陈所走路径为正多边形,设这个正多边形的边数为n,
则20n=360,
解得:n=18,
∴他第一次回到出发点O时一共走了:5×18=90(米),
选:C.
6.解:原式a+1.
选:C.
7.解:设第一批康乃馨的单价是x元,则第二批康乃馨的单价是(x+1)元,
根据题意,.
选:A.
8.解:∵点P(a,3)和点Q(4,b)关于x轴对称,
∴a=4,b=﹣3,
则(a+b)2021=(4﹣3)2021
=1.
选:A.
9.解:∵CA⊥AB于A,DB⊥AB于B,
∴∠A=∠B=90°,
由题意得,BP=t m,BQ=2t m,则AP=(12﹣t)m,
分两种情况:
①若BP=AC,则t=4,
∴AP=12﹣4=8,BQ=8,AP=BQ,
∴△CAP≌△PBQ(SAS);
②若BP=AP,则12﹣t=t,
解得:t=6,BQ=12≠AC,
此时△CAP与△PQB不全等;
综上所述:运动4分钟后△CAP与△PQB全等,则此时t的值是4;
选:A.
10.解;A、当∠A=30°,∠B=60°时,∠C=90°,不是等腰三角形,所以A选项错误.
B、当AB=5,AC=12,BC=13,52+122=132,所以是直角三角形,不是等腰三角形,错误;
C、当A=50°,∠B=80°,∠C=50°,是等腰三角形,正确,
D、当∠A:∠B:∠C=3:4:5,不是等腰三角形,所以D选项错误.
选:C.
二.填空题(共5小题,满分15分,每小题3分)
11.解:过D作DE⊥AB,交AB于点E,
∵∠C=90°,
∴DC⊥CB,
∵BD平分∠ABC,DE⊥BA,
∴DE=DC=6,
即点D到直线AB的距离是6,
答案为:6.
12.解:根据题意得:a﹣2≠0,
解得:a≠2.
答案为:a≠2.
13.解:由y可得,xy=3,
∴矩形的面积=3,
此时矩形能被分割成3个全等的正方形,
则正方形面积为1,边长也为1,
那么图形只有下面一种情况,
其对角线长为,
答案为:.
14.解:x2﹣7x﹣30=(x+3)(x﹣10).
答案为:(x+3)(x﹣10).
15.解:由折叠可知,,∠BED=∠FED,
∵∠ADF=134°,则∠BDF=46°,
∴∠BDE=23°,
∴∠BED=∠FED=180°﹣∠B﹣∠BDE=115°,
则∠CED=180°﹣∠BED=65°,
∴∠CEF=∠FED﹣∠CED=50°,
答案为:50°.
三.解答题(共8小题,满分75分)
16.解:(1)a3﹣4ab2
=a(a2﹣4b2)
=a(a+2b)(a﹣2b);
(2)3ma2﹣18ma+27m
=3m(a2﹣6a+9)
=3m(a﹣3)2.
17.解:(1)原式=﹣6a4b2+9a4b2=3a4b2;
(2)原式=x2+2xy+y2﹣(y2﹣4x2)
=x2+2xy+y2﹣y2+4x2
=5x2+2xy;
(3)原式;
(4)原式.
18.解:(1),
方程两边乘(x﹣2)得:2=x﹣2+1+x,
解得:,
检验:当时,,
∴原分式方程的解为:;
(2)
,
∵分式的值为整数,
∴a﹣1=±2或a﹣1=±1且a(a﹣1)≠0
∴a的值为:2、﹣1、3.
19.证明:∵在△ABD和△ACE中,
,
∴△ABD≌△ACE(AAS),
∴AB=AC.
∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,即∠BAN=∠CAM,
在△BAN和△CAM中,
,
∴△BAN≌△CAM(ASA),
∴∠M=∠N.
20.解:(1)如图,点E、F为所作;
(2)∵BA=BD,BE平分∠ABD,
∴∠ABE=∠DBE=20°,BE⊥AD,AE=DE,
∴∠BED=90°,
∴∠BAE=90°﹣∠ABE=70°,
∵∠BAC=90°,
∴∠DAC=20°,
∵点F为CD的中点,E点为AD的中点,
∴EF为△ADC的中位线,
∴EF∥AC,
∴∠DEF=∠DAC=20°,
∴∠BEF=∠BED+∠DEF=90°+20°=110°.
21.解:(1)由题意可得,
=(a+b) (a﹣b)
;
(2)∵,
∴211,
去分母,得:2+1=x﹣1,
移项及合并同类项,得:x=4,
检验:当x=4时,x﹣1≠0,
∴x=4是原分式方程的解,
即x的值为4.
22.解:(1)根据题意得:(x+y)2﹣2xy=x2+y2;
(2)把a+b=6两边平方得:(a+b)2=36,
整理得:a2+b2+2ab=36,
把a2+b2=10代入得:10+2ab=36,
解得:ab=13;
(3)根据题意得:(y+3x)2=y2+6xy+9x2,
则需要甲型卡片9张、乙型卡片1张、丙型卡片6张.
答案为:9,1,6.
23.[定理探索]已知:在Rt△ABC中,∠ACB=90°,∠BAC=30°,
求证:.
证明:如图,延长BC到D,使CD=BC,
∵∠ACB=90°,
∴AC⊥BD,
又∵CD=BC,
∴AC垂直BD,
∴AB=AD,
在Rt△ABC中,
∵∠ACB=90°,∠ABC=30°,
∴∠ABC=60°,
又∵AB=AD,
∴△ABD是等边三角形,
∴AB=BD,
又∵CD=BC,
∴AB=BD=2BC,
即;
[定理应用](1)解:在△ABC中,AB=AC,∠B=30°,
∴∠C=∠B=30°,∠BAC=120°,
∵AD⊥AB,
∴∠DAB=90°,
∴∠CAD=∠CAB﹣∠DAB=120°﹣90°=30°,
∴∠C=∠CAD,
∴CD=AD,
∵AD=4,
∴BD=2AD=8,
∴BC的长为BD+CD=BD+AD=8+4=12;
选:C.
(2)①解:设∠ADC=α,
∵折叠,
∴∠CDE=α,
∵∠BDE=40°,
∴∠CDB=α﹣40°,
∵∠ADC+CDB=180°,
即α+α﹣40°=180°,
解得:α=110°,
∵∠A=30°,
∴∠ACD=180°﹣∠ADC﹣∠A=40°,
答案为:40.
②解:在△ABC中,
∵∠ACB=90°,∠A=30°,BC=8cm.
∴,
∴AB=2BC=2×8=16(cm),
在△BCD中,
∵CD⊥AB,
∴△BCD是直角三角形,
又∵∠B=60°,
∴,
∴AD=AB﹣BD=16﹣4=12(cm),
∴AD=12cm.
第14页(共14页)
测试时间:100分钟,总分:120分
一.选择题(共10小题,满分30分,每小题3分)
1.下列四个图形中,其中不是轴对称图形的是( )
A. B. C. D.
2.纳米科技是新兴科技,1纳米=0.000000001米,则5纳米用科学记数法表示为( )
A.5×10﹣8米 B.5×10﹣9米 C.5×10﹣10米 D.5×109米
3.下列计算正确的是( )
A.(a2)3=a6 B.a2a3=a C.(2a)3=2a3 D.a10÷a2=a5
4.如图,△ABC中,AB=AC,BD=CE,BF=CD,若∠A=50°,则∠EDF的度数是( )
A.75° B.70° C.65° D.60°
(4题图) (5题图)
5.如图,小陈从O点出发,前进5米后向右转20°,再前进5米后又向右转20°,…,这样一直走下去,他第一次回到出发点O时一共走了( )
A.60米 B.100米 C.90米
6.化简的结果是( )
A.a+a2 B.a﹣1 C.a+1 D.1
7.“五一”前夕,某校社团进行爱心义卖活动,先用800元购进第一批康乃馨,包装后售完,接着又用400元购进第二批康乃馨,已知第二批所购数量是第一批所购数量的,且康乃馨的单价比第一批的单价多1元,设第一批康乃馨的单价是x元,则下列方程正确的是( )
A. B.
C.1 D.1
8.已知点P(a,3)和点Q(4,b)关于x轴对称,则(a+b)2021的值为( )
A.1 B.﹣1 C.72021 D.﹣72021
9.如图,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟是1m,Q点从B向D运动,每分钟走2m,当P、Q两点同时出发t分钟后△CAP全等于△PBQ,则此时t的值是( )
A.4 B.6 C.8 D.10
10.下列条件能判定△ABC为等腰三角形的是( )
A.∠A=30°,∠B=60° B.AB=5,AC=12,BC=13
C.∠A=50°,∠B=80° D.∠A:∠B:∠C=3:4:5
二.填空题(共5小题,满分15分,每小题3分)
11.如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若DC=6,则点D到直线AB的距离= .
12.若分式有意义,则a的取值范围是 .
13.设矩形的两条邻边长分别为x,y,且满足y,若此矩形能被分割成3个全等的正方形,则这个矩形的对角线长是 .
14.分解因式:x2﹣7x﹣30= .
15.如图,在△ABC中,∠B=42°,点D,E分别是BA,BC边上的点,将△BDE沿DE所在直线对折,得到△FDE.若∠ADF=134°,则
∠CEF的度数为 .
三.解答题(共8小题,满分75分)
16.(8分)分解因式:
(1)a3﹣4ab2; (2)3ma2﹣18ma+27m.
17.(12分)计算:
(1)3a3b (﹣2ab)+(﹣3a2b)2; (2)(x+y)2﹣(y+2x)(y﹣2x);
(3)(2ab2c﹣3)﹣2÷(a﹣2b)3; (4).
18.(8分)(1)解方程:;
(2)先化简:,当a为整数时,该代数式的值也为整数,请直接写出所有a值.
19.(8分)如图,∠B=∠C,AD=AE,∠1=∠2.求证:∠M=∠N.
20.(9分)如图,在Rt△ABC中,∠BAC=90°,D是BC边上一点,且BD=BA.
(1)尺规作图:作∠ABC的角平分线交AD于点E,作线段DC的中点F;(保留作图痕迹,不写作法)
(2)连接EF,若∠EBD=20°,求∠BEF的度数.
21.(9分)“”称为二阶行列式,规定它的运算法则为:,例如:.
(1)计算;
(2)求等式中x的值.
22.(10分)【阅读材料】
我们知道,图形也是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙地解决一些图形问题.
在一次数学活动课上,张老师准备了若干张如图1所示的甲、乙、丙三种纸片,其中甲种纸片是边长为x的正方形,乙种纸片是边长为y的正方形,丙种纸片是长为y,宽为x的长方形,并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
【理解应用】
(1)观察图2,请用两种不同方式计算阴影部分的面积,并把得到的等式写出来.
【拓展升华】
(2)利用(1)中的等式解决下列问题.
已知a2+b2=10,a+b=6,求ab的值;
(3)若用图一中的卡片拼成一个边长为y+3x的正方形,则需要甲型卡片 张、乙型卡片 张、丙型卡片 张.
23.(11分)【课本再现】
本学期同学们在学习第十三章《轴对称》,第三单元13.3等腰三角形,第二课13.3.2等边三角形时(P81),学习了一个定理.
定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
【定理探索】
书中对上面的定理没有给出证明,请你结合图形(图1)写出已知、求证并给出定理的证明.
【定理应用】
(1)如图(2),在△ABC中,AB=AC,∠B=30°,AD⊥AB交BC于点D,AD=4,则BC的长为 .
A.8 B.4 C.12 D.6
(2)如图(3),在Rt△ABC中,∠ACB=90°,∠A=30°,BC=8cm.点D是斜边AB上一点,把△ACD沿CD折叠,得到△CDE.
①若∠BDE=40°,则∠ACD= °;
②当折痕CD⊥AB时,求点D的位置(即求AD的长).
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:选项A、C、D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选:B.
2.解:5纳米=0.000000005米=5×10﹣9米.
选:B.
3.解:A.(a2)3=a6,本选项符合题意;
B.a2a3=a5,本选项不符合题意;
C.(2a)3=8a3,本选项不符合题意;
D.a10÷a2=a8,本选项不符合题意.
选:A.
4.解:∵AB=AC、∠A=50°,
∴∠B=∠C(180°﹣∠A)=65°.
在△BDF和△CED中,,
∴△BDF≌△CED(SAS),
∴∠CDE=∠BFD.
∵∠BDF+∠BFD+∠B=180°,∠BDF+∠EDF+∠CDE=180°,
∴∠EDF=∠B=65°.
选:C.
5.解:依题意可知,小陈所走路径为正多边形,设这个正多边形的边数为n,
则20n=360,
解得:n=18,
∴他第一次回到出发点O时一共走了:5×18=90(米),
选:C.
6.解:原式a+1.
选:C.
7.解:设第一批康乃馨的单价是x元,则第二批康乃馨的单价是(x+1)元,
根据题意,.
选:A.
8.解:∵点P(a,3)和点Q(4,b)关于x轴对称,
∴a=4,b=﹣3,
则(a+b)2021=(4﹣3)2021
=1.
选:A.
9.解:∵CA⊥AB于A,DB⊥AB于B,
∴∠A=∠B=90°,
由题意得,BP=t m,BQ=2t m,则AP=(12﹣t)m,
分两种情况:
①若BP=AC,则t=4,
∴AP=12﹣4=8,BQ=8,AP=BQ,
∴△CAP≌△PBQ(SAS);
②若BP=AP,则12﹣t=t,
解得:t=6,BQ=12≠AC,
此时△CAP与△PQB不全等;
综上所述:运动4分钟后△CAP与△PQB全等,则此时t的值是4;
选:A.
10.解;A、当∠A=30°,∠B=60°时,∠C=90°,不是等腰三角形,所以A选项错误.
B、当AB=5,AC=12,BC=13,52+122=132,所以是直角三角形,不是等腰三角形,错误;
C、当A=50°,∠B=80°,∠C=50°,是等腰三角形,正确,
D、当∠A:∠B:∠C=3:4:5,不是等腰三角形,所以D选项错误.
选:C.
二.填空题(共5小题,满分15分,每小题3分)
11.解:过D作DE⊥AB,交AB于点E,
∵∠C=90°,
∴DC⊥CB,
∵BD平分∠ABC,DE⊥BA,
∴DE=DC=6,
即点D到直线AB的距离是6,
答案为:6.
12.解:根据题意得:a﹣2≠0,
解得:a≠2.
答案为:a≠2.
13.解:由y可得,xy=3,
∴矩形的面积=3,
此时矩形能被分割成3个全等的正方形,
则正方形面积为1,边长也为1,
那么图形只有下面一种情况,
其对角线长为,
答案为:.
14.解:x2﹣7x﹣30=(x+3)(x﹣10).
答案为:(x+3)(x﹣10).
15.解:由折叠可知,,∠BED=∠FED,
∵∠ADF=134°,则∠BDF=46°,
∴∠BDE=23°,
∴∠BED=∠FED=180°﹣∠B﹣∠BDE=115°,
则∠CED=180°﹣∠BED=65°,
∴∠CEF=∠FED﹣∠CED=50°,
答案为:50°.
三.解答题(共8小题,满分75分)
16.解:(1)a3﹣4ab2
=a(a2﹣4b2)
=a(a+2b)(a﹣2b);
(2)3ma2﹣18ma+27m
=3m(a2﹣6a+9)
=3m(a﹣3)2.
17.解:(1)原式=﹣6a4b2+9a4b2=3a4b2;
(2)原式=x2+2xy+y2﹣(y2﹣4x2)
=x2+2xy+y2﹣y2+4x2
=5x2+2xy;
(3)原式;
(4)原式.
18.解:(1),
方程两边乘(x﹣2)得:2=x﹣2+1+x,
解得:,
检验:当时,,
∴原分式方程的解为:;
(2)
,
∵分式的值为整数,
∴a﹣1=±2或a﹣1=±1且a(a﹣1)≠0
∴a的值为:2、﹣1、3.
19.证明:∵在△ABD和△ACE中,
,
∴△ABD≌△ACE(AAS),
∴AB=AC.
∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,即∠BAN=∠CAM,
在△BAN和△CAM中,
,
∴△BAN≌△CAM(ASA),
∴∠M=∠N.
20.解:(1)如图,点E、F为所作;
(2)∵BA=BD,BE平分∠ABD,
∴∠ABE=∠DBE=20°,BE⊥AD,AE=DE,
∴∠BED=90°,
∴∠BAE=90°﹣∠ABE=70°,
∵∠BAC=90°,
∴∠DAC=20°,
∵点F为CD的中点,E点为AD的中点,
∴EF为△ADC的中位线,
∴EF∥AC,
∴∠DEF=∠DAC=20°,
∴∠BEF=∠BED+∠DEF=90°+20°=110°.
21.解:(1)由题意可得,
=(a+b) (a﹣b)
;
(2)∵,
∴211,
去分母,得:2+1=x﹣1,
移项及合并同类项,得:x=4,
检验:当x=4时,x﹣1≠0,
∴x=4是原分式方程的解,
即x的值为4.
22.解:(1)根据题意得:(x+y)2﹣2xy=x2+y2;
(2)把a+b=6两边平方得:(a+b)2=36,
整理得:a2+b2+2ab=36,
把a2+b2=10代入得:10+2ab=36,
解得:ab=13;
(3)根据题意得:(y+3x)2=y2+6xy+9x2,
则需要甲型卡片9张、乙型卡片1张、丙型卡片6张.
答案为:9,1,6.
23.[定理探索]已知:在Rt△ABC中,∠ACB=90°,∠BAC=30°,
求证:.
证明:如图,延长BC到D,使CD=BC,
∵∠ACB=90°,
∴AC⊥BD,
又∵CD=BC,
∴AC垂直BD,
∴AB=AD,
在Rt△ABC中,
∵∠ACB=90°,∠ABC=30°,
∴∠ABC=60°,
又∵AB=AD,
∴△ABD是等边三角形,
∴AB=BD,
又∵CD=BC,
∴AB=BD=2BC,
即;
[定理应用](1)解:在△ABC中,AB=AC,∠B=30°,
∴∠C=∠B=30°,∠BAC=120°,
∵AD⊥AB,
∴∠DAB=90°,
∴∠CAD=∠CAB﹣∠DAB=120°﹣90°=30°,
∴∠C=∠CAD,
∴CD=AD,
∵AD=4,
∴BD=2AD=8,
∴BC的长为BD+CD=BD+AD=8+4=12;
选:C.
(2)①解:设∠ADC=α,
∵折叠,
∴∠CDE=α,
∵∠BDE=40°,
∴∠CDB=α﹣40°,
∵∠ADC+CDB=180°,
即α+α﹣40°=180°,
解得:α=110°,
∵∠A=30°,
∴∠ACD=180°﹣∠ADC﹣∠A=40°,
答案为:40.
②解:在△ABC中,
∵∠ACB=90°,∠A=30°,BC=8cm.
∴,
∴AB=2BC=2×8=16(cm),
在△BCD中,
∵CD⊥AB,
∴△BCD是直角三角形,
又∵∠B=60°,
∴,
∴AD=AB﹣BD=16﹣4=12(cm),
∴AD=12cm.
第14页(共14页)
同课章节目录
