27.3 课时1 弧长和扇形的面积 课件(共17张PPT) 华师大版数学九年级下册
文档属性
| 名称 | 27.3 课时1 弧长和扇形的面积 课件(共17张PPT) 华师大版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-06 13:16:18 | ||
图片预览



文档简介
(共17张PPT)
27.3 课时1 弧长和扇形的面积
1.探索并理解弧长和扇形面积公式
2.会利用弧长和扇形面积的计算公式进行计算.
你注意到了吗,在运动会的200米比赛中,各选手的起跑线不在同一处,你知道这是为什么吗?
因为要保证这些弯道的“展直长度”是一样的.
那我们应该怎样来计算弯道的“展直长度”?
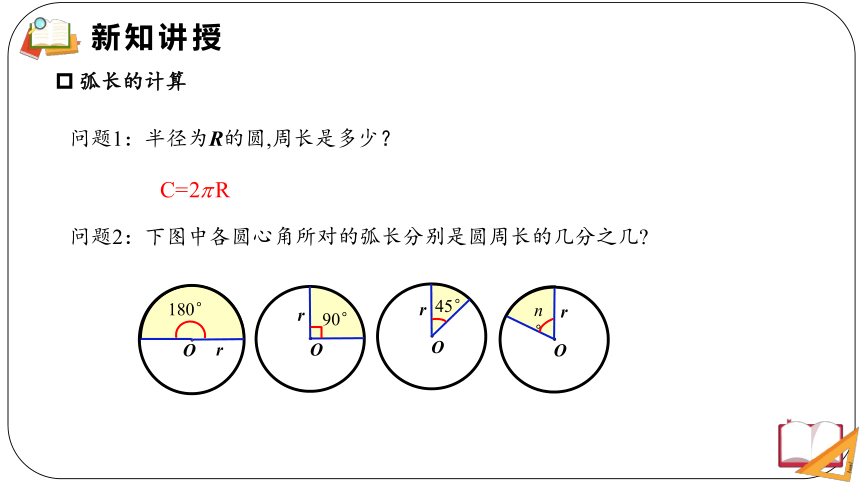
弧长的计算
问题1:半径为R的圆,周长是多少?
问题2:下图中各圆心角所对的弧长分别是圆周长的几分之几
O
r
90°
O
r
45°
O
r
n°
O
r
180°
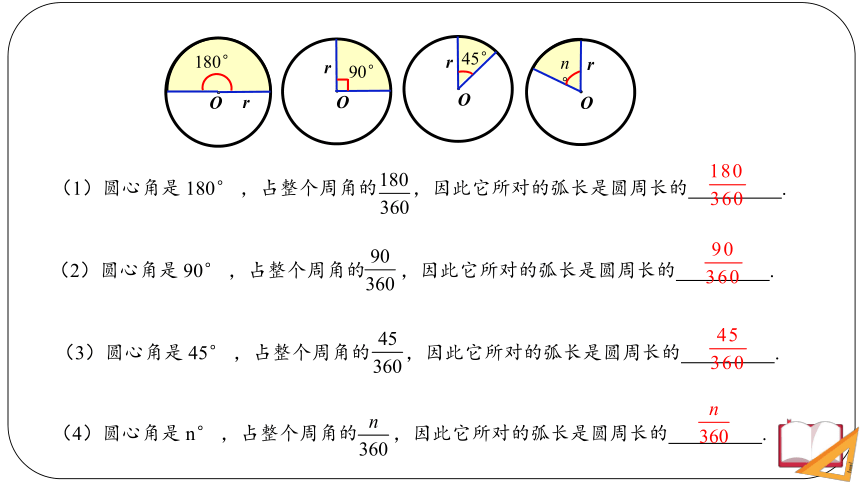
(1)圆心角是 180° ,占整个周角的 ,因此它所对的弧长是圆周长的 .
(2)圆心角是 90° ,占整个周角的 ,因此它所对的弧长是圆周长的 .
(3)圆心角是 45° ,占整个周角的 ,因此它所对的弧长是圆周长的 .
(4)圆心角是 n° ,占整个周角的 ,因此它所对的弧长是圆周长的 .
O
r
90°
O
r
45°
O
r
n°
O
r
180°
O
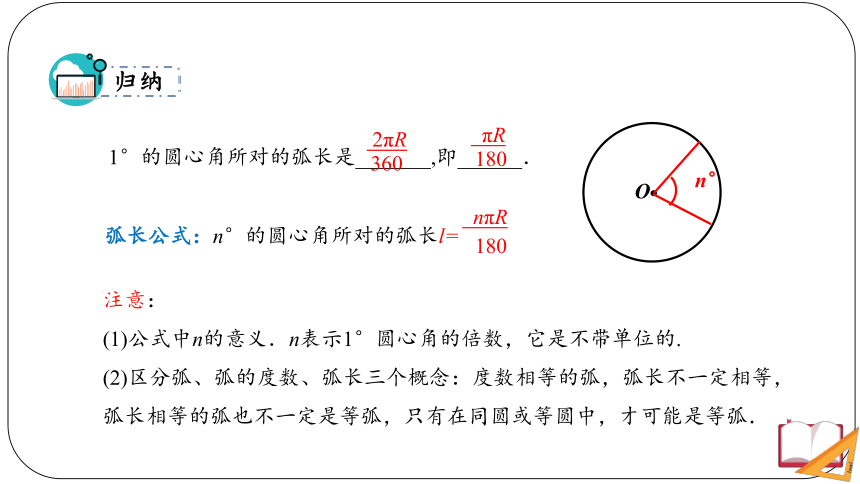
1°的圆心角所对的弧长是_______,即______.
2πR
360
πR
180
弧长公式:n°的圆心角所对的弧长l=
nπR
180
n°
归纳
注意:
(1)公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
(2)区分弧、弧的度数、弧长三个概念:度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等弧,只有在同圆或等圆中,才可能是等弧.
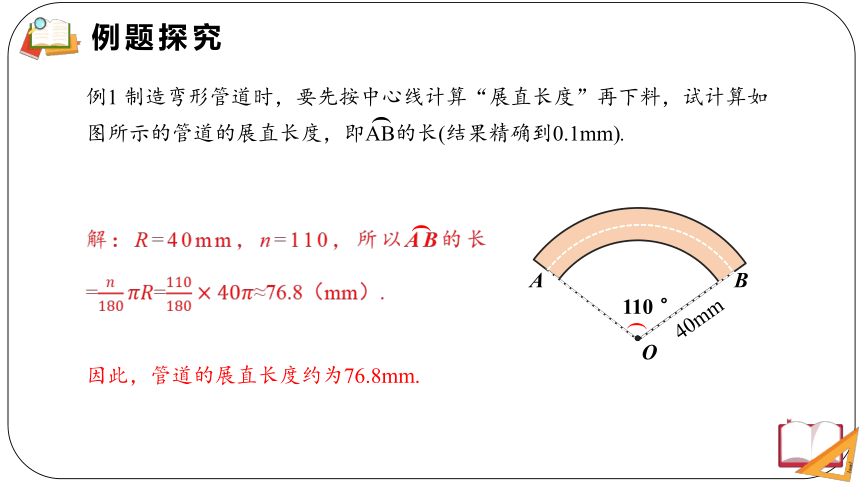
例1 制造弯形管道时,要先按中心线计算“展直长度”再下料,试计算如图所示的管道的展直长度,即AB的长(结果精确到0.1mm).
解:R=40mm,n=110,所以AB的长==≈76.8(mm).
因此,管道的展直长度约为76.8mm.
(
110 °
A
B
O
)
)
40mm
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形.
扇形的定义:
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
扇形面积的计算
概念
大家想一想,生活中有哪些扇形的物体 ?
扇形面积计算
问题1:半径为r的圆,面积是多少?
问题2:下图中各圆心角所对的扇形的面积分别是圆面积的几分之几 填写表格
O
r
90°
O
r
45°
O
r
n°
O
r
180°
圆心角占
周角的比例 扇形面积占
圆面积的比例 扇形
的面积
O
n°
R
1°的圆心角所对的扇形面积是_____.
πR2
360
公式:n°的圆心角所对的扇形面积 S扇形=
nπR2
360
对比弧长公式可以得到
S扇形= lR
2
1
归纳
例2 如图,圆心角为 60° 的扇形的半径为 10 cm. 求这个扇形的面积和周长(精确到 0.01 cm2 和 0.01 cm).
O
r
60°
解:∵ n = 60,r = 10 cm,
∴ 扇形的面积为
该扇形的周长为
B
A
≈30.47(cm).
≈52.36(cm2).
S弓形=S扇形-S三角形 S弓形=S扇形+S三角形
O
O
弓形的面积=扇形的面积±三角形的面积(割补法)
如图,由弦及其所对的弧组成的图形叫做弓形.
知识补充
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π B.2π C.3π D.6π
2.已知一个扇形的半径为6,弧长为2π,则这个扇形的圆心角为( )
A.30° B.60° C.90° D.120°
C
B
4.如图,⊙A、 ⊙B、 ⊙C、 ⊙D 两两不相交,且半径都是 2 cm,则图中阴影部分的面积是 .
A
B
C
D
180°
3.若一个扇形的半径为2 cm,面积为2π cm2,则此扇形的圆心角为 .
5.如图,扇形的圆心角为90°,半径OC=2,∠AOC=30°,CD⊥OB于点D,求阴影部分的面积.
解:∵∠AOB=90°,∠AOC=30°,
∴∠BOC=60°.
∵CD⊥OB,
∴∠CDO=90°,
∴OD=OC=1,CD=OD=,
∴阴影部分的面积=S扇形BOC -S△COD=×1×π-.
弧长
计算公式:
扇形
公式
阴影部分面积
求法:整体思想
弓形
公式
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
27.3 课时1 弧长和扇形的面积
1.探索并理解弧长和扇形面积公式
2.会利用弧长和扇形面积的计算公式进行计算.
你注意到了吗,在运动会的200米比赛中,各选手的起跑线不在同一处,你知道这是为什么吗?
因为要保证这些弯道的“展直长度”是一样的.
那我们应该怎样来计算弯道的“展直长度”?
弧长的计算
问题1:半径为R的圆,周长是多少?
问题2:下图中各圆心角所对的弧长分别是圆周长的几分之几
O
r
90°
O
r
45°
O
r
n°
O
r
180°
(1)圆心角是 180° ,占整个周角的 ,因此它所对的弧长是圆周长的 .
(2)圆心角是 90° ,占整个周角的 ,因此它所对的弧长是圆周长的 .
(3)圆心角是 45° ,占整个周角的 ,因此它所对的弧长是圆周长的 .
(4)圆心角是 n° ,占整个周角的 ,因此它所对的弧长是圆周长的 .
O
r
90°
O
r
45°
O
r
n°
O
r
180°
O
1°的圆心角所对的弧长是_______,即______.
2πR
360
πR
180
弧长公式:n°的圆心角所对的弧长l=
nπR
180
n°
归纳
注意:
(1)公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
(2)区分弧、弧的度数、弧长三个概念:度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等弧,只有在同圆或等圆中,才可能是等弧.
例1 制造弯形管道时,要先按中心线计算“展直长度”再下料,试计算如图所示的管道的展直长度,即AB的长(结果精确到0.1mm).
解:R=40mm,n=110,所以AB的长==≈76.8(mm).
因此,管道的展直长度约为76.8mm.
(
110 °
A
B
O
)
)
40mm
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形.
扇形的定义:
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
扇形面积的计算
概念
大家想一想,生活中有哪些扇形的物体 ?
扇形面积计算
问题1:半径为r的圆,面积是多少?
问题2:下图中各圆心角所对的扇形的面积分别是圆面积的几分之几 填写表格
O
r
90°
O
r
45°
O
r
n°
O
r
180°
圆心角占
周角的比例 扇形面积占
圆面积的比例 扇形
的面积
O
n°
R
1°的圆心角所对的扇形面积是_____.
πR2
360
公式:n°的圆心角所对的扇形面积 S扇形=
nπR2
360
对比弧长公式可以得到
S扇形= lR
2
1
归纳
例2 如图,圆心角为 60° 的扇形的半径为 10 cm. 求这个扇形的面积和周长(精确到 0.01 cm2 和 0.01 cm).
O
r
60°
解:∵ n = 60,r = 10 cm,
∴ 扇形的面积为
该扇形的周长为
B
A
≈30.47(cm).
≈52.36(cm2).
S弓形=S扇形-S三角形 S弓形=S扇形+S三角形
O
O
弓形的面积=扇形的面积±三角形的面积(割补法)
如图,由弦及其所对的弧组成的图形叫做弓形.
知识补充
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π B.2π C.3π D.6π
2.已知一个扇形的半径为6,弧长为2π,则这个扇形的圆心角为( )
A.30° B.60° C.90° D.120°
C
B
4.如图,⊙A、 ⊙B、 ⊙C、 ⊙D 两两不相交,且半径都是 2 cm,则图中阴影部分的面积是 .
A
B
C
D
180°
3.若一个扇形的半径为2 cm,面积为2π cm2,则此扇形的圆心角为 .
5.如图,扇形的圆心角为90°,半径OC=2,∠AOC=30°,CD⊥OB于点D,求阴影部分的面积.
解:∵∠AOB=90°,∠AOC=30°,
∴∠BOC=60°.
∵CD⊥OB,
∴∠CDO=90°,
∴OD=OC=1,CD=OD=,
∴阴影部分的面积=S扇形BOC -S△COD=×1×π-.
弧长
计算公式:
扇形
公式
阴影部分面积
求法:整体思想
弓形
公式
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
