第10 章相交线,平行线与平移基础复习 (二)(含答案)沪科版数学七年级下册
文档属性
| 名称 | 第10 章相交线,平行线与平移基础复习 (二)(含答案)沪科版数学七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 252.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-07 00:00:00 | ||
图片预览


文档简介
第10 章相交线,平行线与平移基础复习 (二)
知识点 1 平行线的性质
1. 两直线平行,同位角相等.
2. 两直线平行,内错角相等.
3. 两直线平行,同旁内角互补.
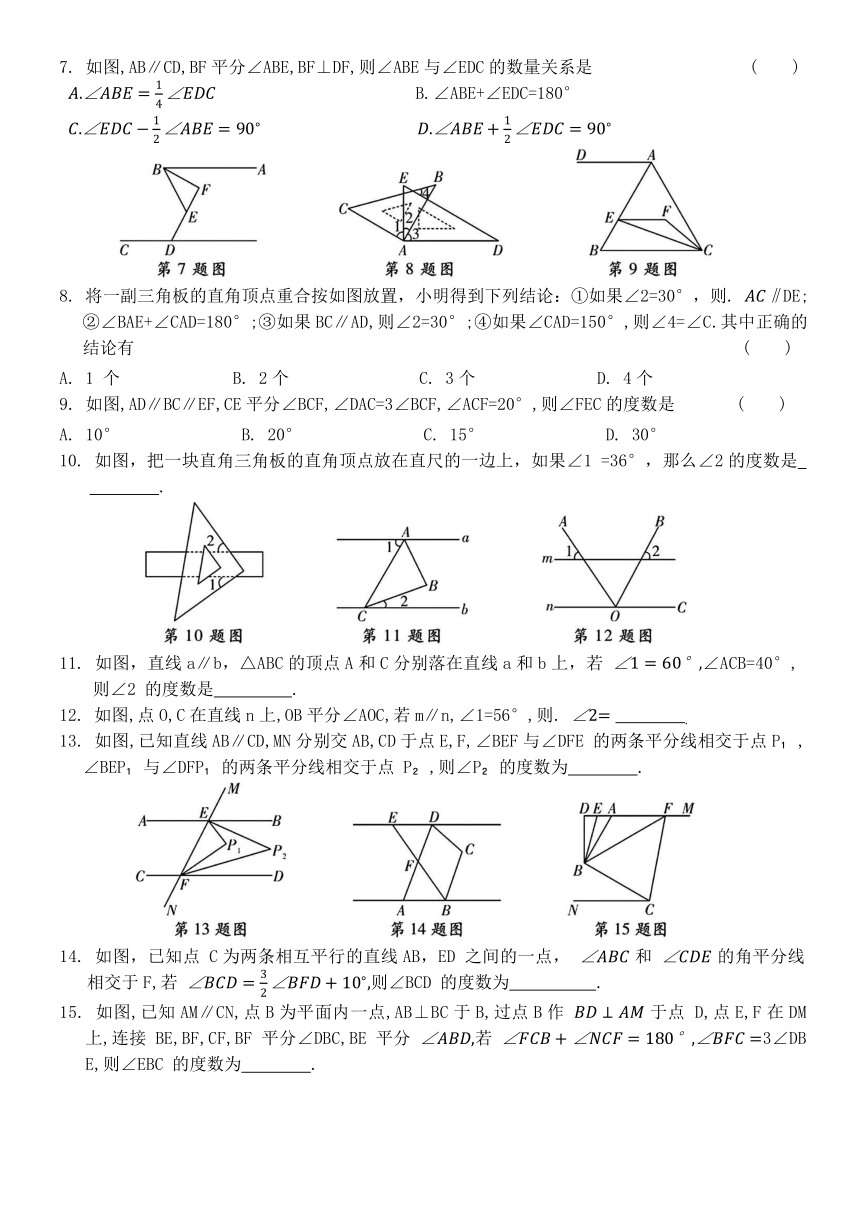
1. 如图,直线 ,则∠2的度数为 ( )
A. 40° B. 50° C. 55° D. 60°
2. 如图,DA⊥AB,CD⊥DA,∠B=56°,则∠C的度数是 ( )
B. 144° C. 134° D. 124°
3. 如图,已知AB∥DE,∠1 =30°,∠2=35°,则∠BCE的度数为 ( )
A. 70° B. 65° C. 35° D. 5°
4. 如图,直线AB∥CD,∠B=40°,∠C=50°,则∠E的度数是 ( )
A. 70° B. 80° C. 90° D. 100°
5. 将一张矩形纸片折叠成如图所示的图形,若∠CAB=30°,则∠ACB的度数是 ( )
A. 45° B. 55° C. 65° D. 75°
6. 如图,AB∥CD,∠EFD=64°,∠FEB的角平分线EG交CD于点 G,则∠GEB的度数为 ( )
B. 56° C. 68° D. 58°
7. 如图,AB∥CD,BF平分∠ABE,BF⊥DF,则∠ABE与∠EDC的数量关系是 ( )
B.∠ABE+∠EDC=180°
8. 将一副三角板的直角顶点重合按如图放置,小明得到下列结论:①如果∠2=30°,则. DE;②∠BAE+∠CAD=180°;③如果BC∥AD,则∠2=30°;④如果∠CAD=150°,则∠4=∠C.其中正确的结论有 ( )
A. 1 个 B. 2个 C. 3个 D. 4个
9. 如图,AD∥BC∥EF,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°,则∠FEC的度数是 ( )
A. 10° B. 20° C. 15° D. 30°
10. 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1 =36°,那么∠2的度数是 .
11. 如图,直线a∥b,△ABC的顶点A和C分别落在直线a和b上,若 ∠ACB=40°,则∠2 的度数是 .
12. 如图,点O,C在直线n上,OB平分∠AOC,若m∥n,∠1=56°,则.
13. 如图,已知直线AB∥CD,MN分别交AB,CD于点E,F,∠BEF与∠DFE 的两条平分线相交于点P ,∠BEP 与∠DFP 的两条平分线相交于点 P ,则∠P 的度数为 .
14. 如图,已知点 C为两条相互平行的直线AB,ED 之间的一点, 和 的角平分线相交于F,若 则∠BCD 的度数为 .
15. 如图,已知AM∥CN,点B为平面内一点,AB⊥BC于B,过点B作 于点 D,点E,F在DM上,连接 BE,BF,CF,BF 平分∠DBC,BE 平分 若 3∠DBE,则∠EBC 的度数为 .
16. 如图, ,BF平分 ,DE 平分 问AB与 CD,AD 与 BC平行吗 请说明理由.
17. 如图,已知
(1)EF 与 BH平行吗 请说明理由.
(2)若BH平分 于点 F, 求 的度数.
知识点 2 平移
1. 在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.
2. 一个图形和它经过平移后所得的图形中,连接各组对应点的线段互相平行(或在同一条直线上)且相等.
3. 平移只改变图形的位置,不改变图形的形状和大小.
18. 如图,三角形ABC沿AC方向平移得到三角形DEF,已知 那么平移的距离为 ( )
A. 3 B. 4
C. 5 D. 7
19. 下列选项中,两个三角形通过平移能重合的是 ( )
20. 如图,三角形ABC沿AB 方向向右平移后到达三角形 的位置,BC与 相交于点O,若∠C 的度数为x,则∠A OC 的度数为 ( )
A. x B. 90°-x
21. 如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中是平移重合图形的是 ( )
A. 平行四边形 B. 等腰梯形 C. 正六边形 D. 圆
22. 如图,将三角形ABC沿水平方向向右平移到三角形 DEF的位置,已知点A,D之间的距离为5,CE=7,则BF的长为 .
23. 如图,三角形ABC中,BC=4 cm.现将三角形 ABC沿着垂直于BC的方向平移5cm,到 的位置,则△ABC的边AC,AB所扫过的面积是 cm .
24. 如图,将三角形ABC水平向右平移得到三角形DEF,A,D两点的距离为1, 根据题意完成下列各题:
(1)AC 和 DF 的数量关系为 ;AC 和 DF 的位置关系为 .
(2)∠1= 度.
(3)BF= .
25. 如图,已知三角形ABC中,∠ABC=90°,边BC=12cm,把三角形ABC向下平移至三角形DEF后,AD=5cm,GC=4cm,请求出图中阴影部分的面积.
第10章相交线,平行线与平移基础复习(二)
1. B 2. D 3. B 4. C 5. D 6. D 7. C 8. C 9. B10. 54° 11. 20° 12. 62° 13. 45° 14. 160° 15. 105°
16. 解:AB与CD,AD与BC平行.理由如下:
因为BF平分∠ABC,DE平分∠ADC,
所以
因为∠ABC=∠ADC,所以∠ABF=∠CDE,
因为DE∥BF,所以∠AED=∠ABF,
所以∠AED=∠ABF=∠CDE,所以AB∥CD,
所以∠ADC+∠A=180°,
因为∠ABC=∠ADC,所以∠ABC+∠A=180°,所以AD∥BC.
17. 解:(1)EF 与BH平行.理由如下:
因为∠HCO=∠EBC,所以EB∥HC.
所以∠EBH=∠BHC.
因为∠BHC+∠BEF=180°,
所以∠EBH+∠BEF=180°.所以EF∥BH.(2)因为∠HCO=∠EBC,∠HCO=64°,所以∠EBC=64°,因为BH平分∠EBO,所以
由(1)知∠EBH=∠BHC,所以∠BHC=32°.
因为EF⊥AO于F,EF∥BH,所以∠BHA=90°.
所以∠FHC=∠BHA +∠BHC=122°.
因为∠CHO +∠FHC =180°,所以∠CHO =180°--∠FHC =180°-122°=58°.
18. B 19. B 20. C 21. A 22. 17 23. 20
24. 解:(1)因为三角形ABC水平向右平移得到三角形 DEF,所以AC=DF,AC∥DF.
故答案为:AC=DF;AC∥DF.
(2)因为△ABC水平向右平移得到△DEF,
所以∠D=∠A=70°,AC∥DF.
所以∠1+∠D=180°.
所以∠1=180°-∠D=110°.
(3)因为A,D两点的距离为1,所以BE=CF=1.
所以BF=BE+EC+CF=1+2+1=4.
25. 解:因为三角形ABC向下平移得到三角形 DEF,所以AB =DE,BC=EF,S三角形ABC =S三角形DEF
所以AD=BE,阴影部分面积=梯形 BGEF的面积,
因为BC=12 cm,AD=5cm,GC=4 cm,
所以BG=BC-GC=8cm,BE=5cm,所以阴影部分面积
知识点 1 平行线的性质
1. 两直线平行,同位角相等.
2. 两直线平行,内错角相等.
3. 两直线平行,同旁内角互补.
1. 如图,直线 ,则∠2的度数为 ( )
A. 40° B. 50° C. 55° D. 60°
2. 如图,DA⊥AB,CD⊥DA,∠B=56°,则∠C的度数是 ( )
B. 144° C. 134° D. 124°
3. 如图,已知AB∥DE,∠1 =30°,∠2=35°,则∠BCE的度数为 ( )
A. 70° B. 65° C. 35° D. 5°
4. 如图,直线AB∥CD,∠B=40°,∠C=50°,则∠E的度数是 ( )
A. 70° B. 80° C. 90° D. 100°
5. 将一张矩形纸片折叠成如图所示的图形,若∠CAB=30°,则∠ACB的度数是 ( )
A. 45° B. 55° C. 65° D. 75°
6. 如图,AB∥CD,∠EFD=64°,∠FEB的角平分线EG交CD于点 G,则∠GEB的度数为 ( )
B. 56° C. 68° D. 58°
7. 如图,AB∥CD,BF平分∠ABE,BF⊥DF,则∠ABE与∠EDC的数量关系是 ( )
B.∠ABE+∠EDC=180°
8. 将一副三角板的直角顶点重合按如图放置,小明得到下列结论:①如果∠2=30°,则. DE;②∠BAE+∠CAD=180°;③如果BC∥AD,则∠2=30°;④如果∠CAD=150°,则∠4=∠C.其中正确的结论有 ( )
A. 1 个 B. 2个 C. 3个 D. 4个
9. 如图,AD∥BC∥EF,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°,则∠FEC的度数是 ( )
A. 10° B. 20° C. 15° D. 30°
10. 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1 =36°,那么∠2的度数是 .
11. 如图,直线a∥b,△ABC的顶点A和C分别落在直线a和b上,若 ∠ACB=40°,则∠2 的度数是 .
12. 如图,点O,C在直线n上,OB平分∠AOC,若m∥n,∠1=56°,则.
13. 如图,已知直线AB∥CD,MN分别交AB,CD于点E,F,∠BEF与∠DFE 的两条平分线相交于点P ,∠BEP 与∠DFP 的两条平分线相交于点 P ,则∠P 的度数为 .
14. 如图,已知点 C为两条相互平行的直线AB,ED 之间的一点, 和 的角平分线相交于F,若 则∠BCD 的度数为 .
15. 如图,已知AM∥CN,点B为平面内一点,AB⊥BC于B,过点B作 于点 D,点E,F在DM上,连接 BE,BF,CF,BF 平分∠DBC,BE 平分 若 3∠DBE,则∠EBC 的度数为 .
16. 如图, ,BF平分 ,DE 平分 问AB与 CD,AD 与 BC平行吗 请说明理由.
17. 如图,已知
(1)EF 与 BH平行吗 请说明理由.
(2)若BH平分 于点 F, 求 的度数.
知识点 2 平移
1. 在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.
2. 一个图形和它经过平移后所得的图形中,连接各组对应点的线段互相平行(或在同一条直线上)且相等.
3. 平移只改变图形的位置,不改变图形的形状和大小.
18. 如图,三角形ABC沿AC方向平移得到三角形DEF,已知 那么平移的距离为 ( )
A. 3 B. 4
C. 5 D. 7
19. 下列选项中,两个三角形通过平移能重合的是 ( )
20. 如图,三角形ABC沿AB 方向向右平移后到达三角形 的位置,BC与 相交于点O,若∠C 的度数为x,则∠A OC 的度数为 ( )
A. x B. 90°-x
21. 如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中是平移重合图形的是 ( )
A. 平行四边形 B. 等腰梯形 C. 正六边形 D. 圆
22. 如图,将三角形ABC沿水平方向向右平移到三角形 DEF的位置,已知点A,D之间的距离为5,CE=7,则BF的长为 .
23. 如图,三角形ABC中,BC=4 cm.现将三角形 ABC沿着垂直于BC的方向平移5cm,到 的位置,则△ABC的边AC,AB所扫过的面积是 cm .
24. 如图,将三角形ABC水平向右平移得到三角形DEF,A,D两点的距离为1, 根据题意完成下列各题:
(1)AC 和 DF 的数量关系为 ;AC 和 DF 的位置关系为 .
(2)∠1= 度.
(3)BF= .
25. 如图,已知三角形ABC中,∠ABC=90°,边BC=12cm,把三角形ABC向下平移至三角形DEF后,AD=5cm,GC=4cm,请求出图中阴影部分的面积.
第10章相交线,平行线与平移基础复习(二)
1. B 2. D 3. B 4. C 5. D 6. D 7. C 8. C 9. B10. 54° 11. 20° 12. 62° 13. 45° 14. 160° 15. 105°
16. 解:AB与CD,AD与BC平行.理由如下:
因为BF平分∠ABC,DE平分∠ADC,
所以
因为∠ABC=∠ADC,所以∠ABF=∠CDE,
因为DE∥BF,所以∠AED=∠ABF,
所以∠AED=∠ABF=∠CDE,所以AB∥CD,
所以∠ADC+∠A=180°,
因为∠ABC=∠ADC,所以∠ABC+∠A=180°,所以AD∥BC.
17. 解:(1)EF 与BH平行.理由如下:
因为∠HCO=∠EBC,所以EB∥HC.
所以∠EBH=∠BHC.
因为∠BHC+∠BEF=180°,
所以∠EBH+∠BEF=180°.所以EF∥BH.(2)因为∠HCO=∠EBC,∠HCO=64°,所以∠EBC=64°,因为BH平分∠EBO,所以
由(1)知∠EBH=∠BHC,所以∠BHC=32°.
因为EF⊥AO于F,EF∥BH,所以∠BHA=90°.
所以∠FHC=∠BHA +∠BHC=122°.
因为∠CHO +∠FHC =180°,所以∠CHO =180°--∠FHC =180°-122°=58°.
18. B 19. B 20. C 21. A 22. 17 23. 20
24. 解:(1)因为三角形ABC水平向右平移得到三角形 DEF,所以AC=DF,AC∥DF.
故答案为:AC=DF;AC∥DF.
(2)因为△ABC水平向右平移得到△DEF,
所以∠D=∠A=70°,AC∥DF.
所以∠1+∠D=180°.
所以∠1=180°-∠D=110°.
(3)因为A,D两点的距离为1,所以BE=CF=1.
所以BF=BE+EC+CF=1+2+1=4.
25. 解:因为三角形ABC向下平移得到三角形 DEF,所以AB =DE,BC=EF,S三角形ABC =S三角形DEF
所以AD=BE,阴影部分面积=梯形 BGEF的面积,
因为BC=12 cm,AD=5cm,GC=4 cm,
所以BG=BC-GC=8cm,BE=5cm,所以阴影部分面积
