1.1 从梯子的倾斜程度谈起课件(共36张PPT)
文档属性
| 名称 | 1.1 从梯子的倾斜程度谈起课件(共36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 310.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-14 00:00:00 | ||
图片预览

文档简介
课件36张PPT。第一章
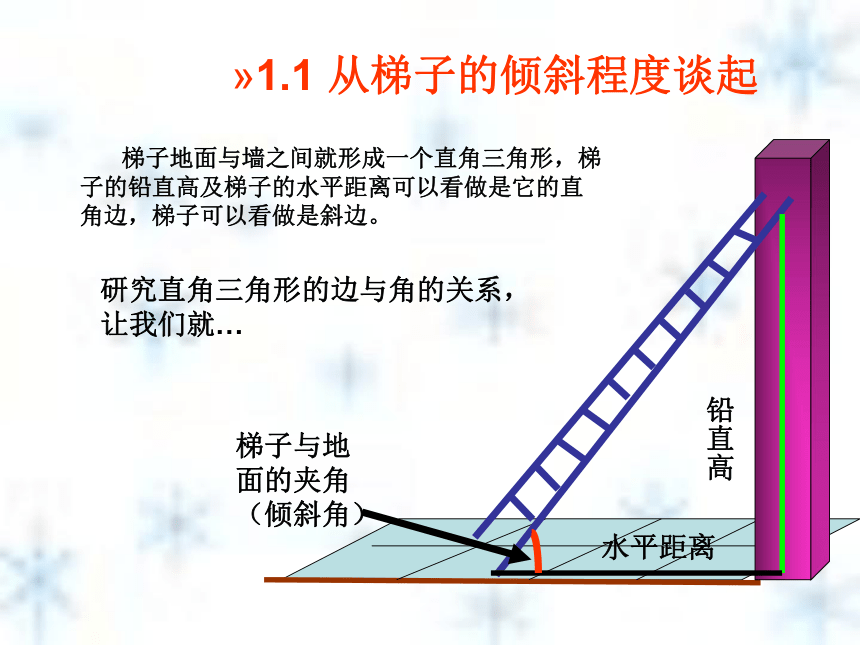
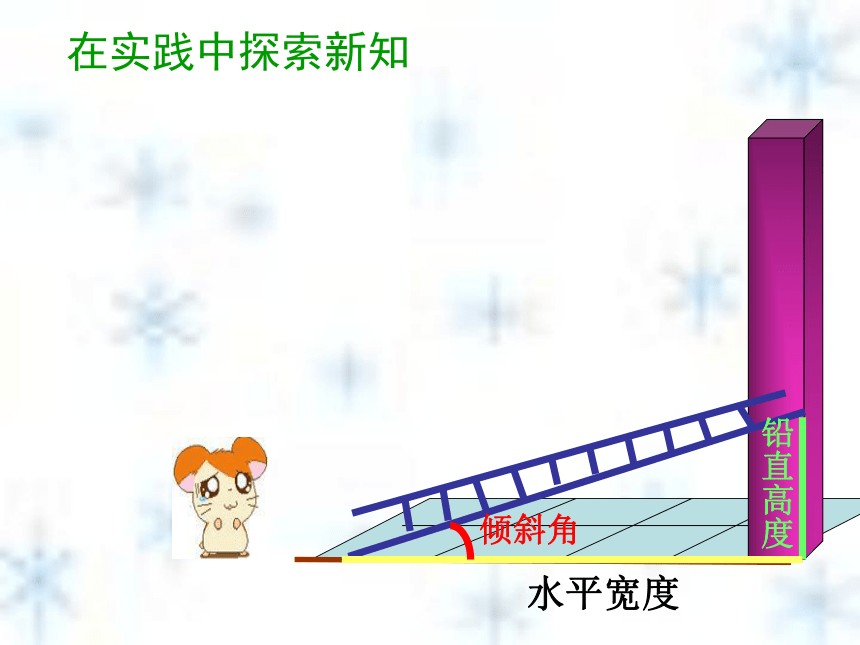
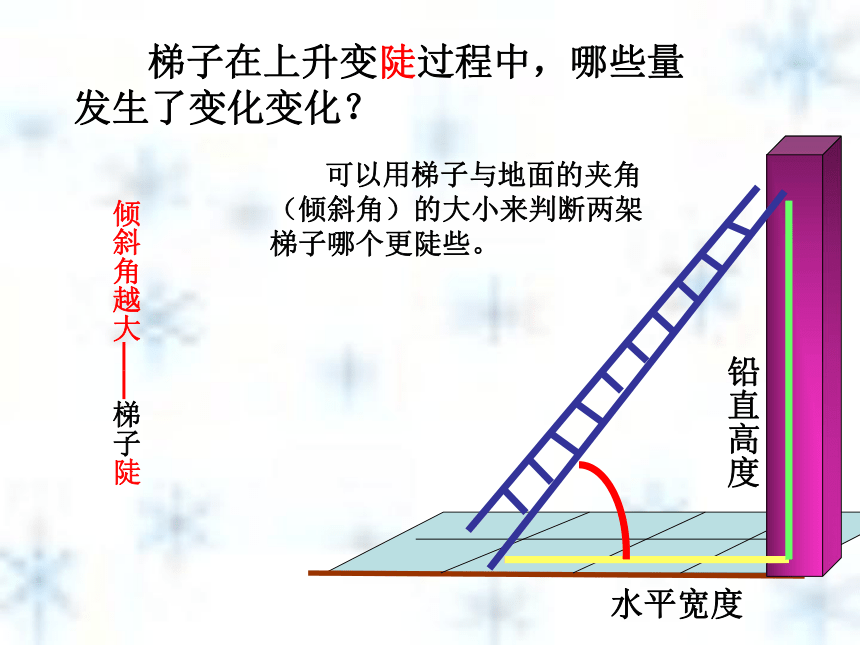
直角三角形的边角关系1.1 从梯子的倾斜程度谈起 梯子地面与墙之间就形成一个直角三角形,梯子的铅直高及梯子的水平距离可以看做是它的直角边,梯子可以看做是斜边。铅直高水平距离研究直角三角形的边与角的关系,让我们就…梯子与地面的夹角(倾斜角)水平宽度铅直高度倾斜角在实践中探索新知在实践中探索新知变陡了吗?在实践中探索新知变陡了吗?在实践中探索新知变陡了吗?在实践中探索新知变陡了吗? 梯子在上升变陡过程中,哪些量发生了变化变化?
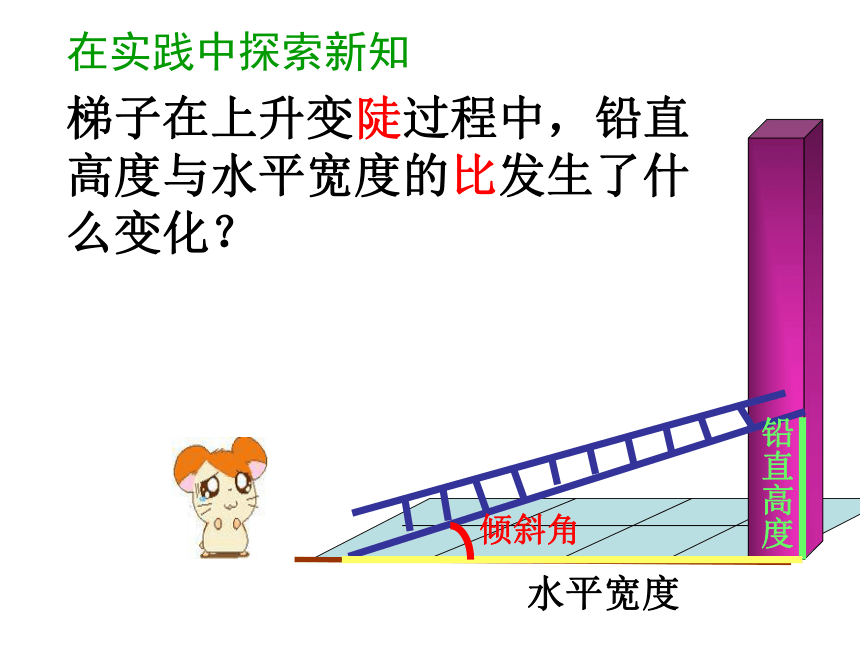
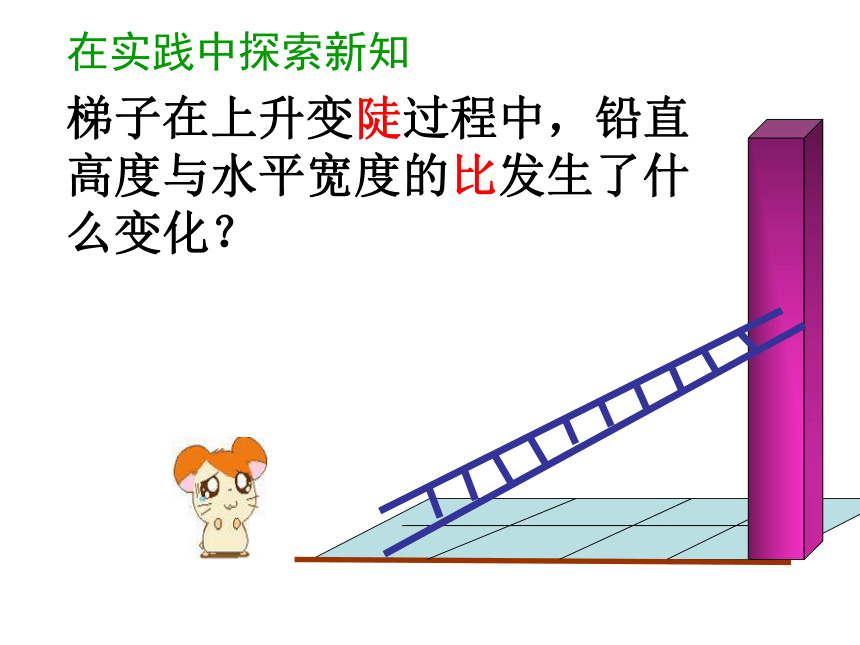
铅直高度 水平宽度
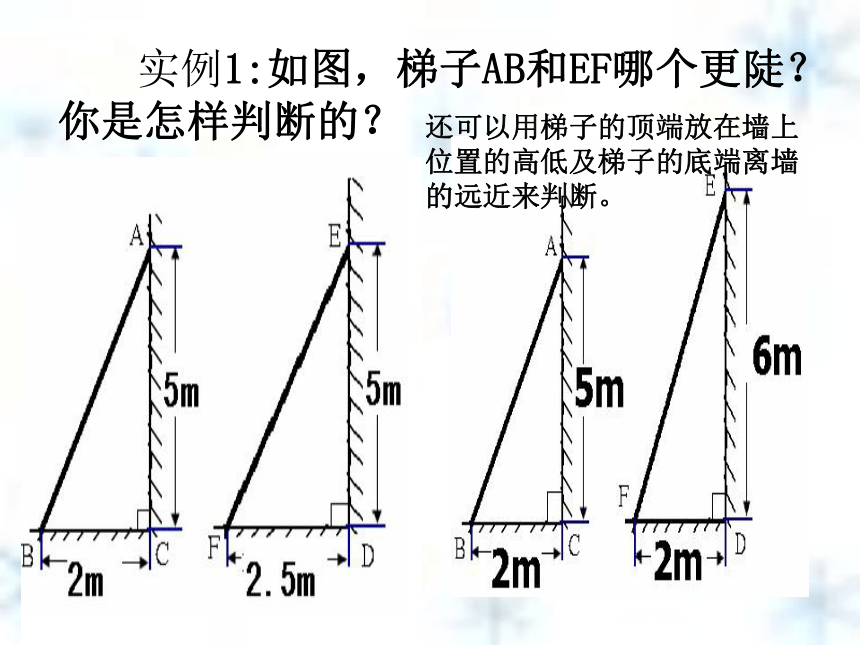
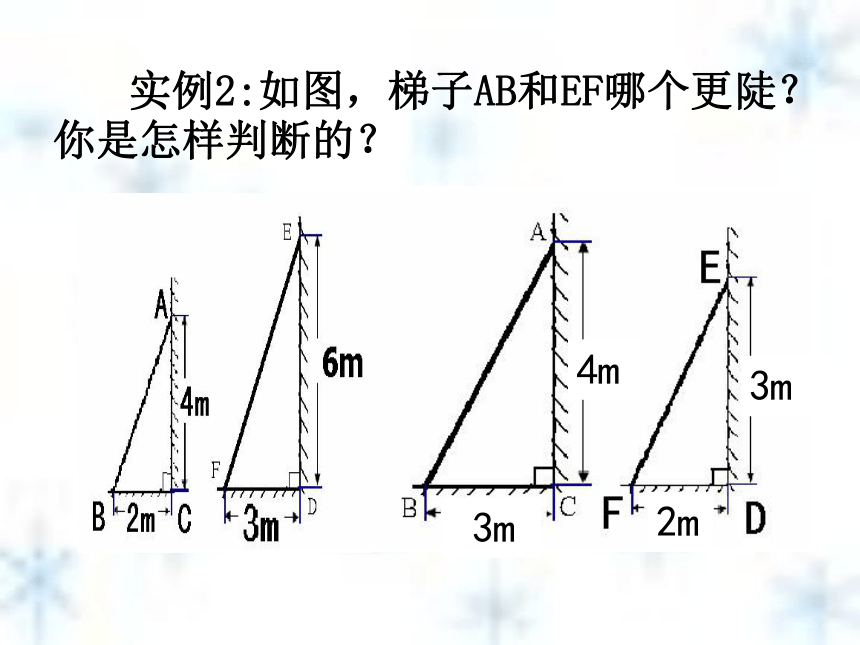
倾斜角越大——梯子陡 可以用梯子与地面的夹角(倾斜角)的大小来判断两架梯子哪个更陡些。 实例1:如图,梯子AB和EF哪个更陡?你是怎样判断的?还可以用梯子的顶端放在墙上位置的高低及梯子的底端离墙的远近来判断。 实例2:如图,梯子AB和EF哪个更陡?你是怎样判断的?梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 水平宽度铅直高度倾斜角在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知 实例2:如图,梯子AB和EF哪个更陡?你是怎样判断的?梯子的铅直高与其水平距离的比相同时,梯子就一样陡。比值大的梯子陡。 若小明因身高原因不能顺利测量梯子顶端到墙脚的距离B1 C1 ,进而无法刻画梯子的倾斜程度,他该怎么办?你有什么锦囊妙计? AC1B1驶向胜利的彼岸请你想一想 AB1 C1 C2B2 如果改变B2在梯子上的位置呢?由此你能得出什么结论?由感性到理性请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2 AB1 C1 C2B2由感性到理性请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2 如果改变B2在梯子上的位置呢?由此你能得出什么结论? AB1 C1 C2B2请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2由感性到理性 如果改变B2在梯子上的位置呢?由此你能得出什么结论? AB1 C1 C2B2请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2由感性到理性 如果改变B2在梯子上的位置呢?由此你能得出什么结论? AB1 C1 C2B2请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2由感性到理性 如果改变B2在梯子上的位置呢?由此你能得出什么结论?任意改变B2在梯子上的位置,则:∠A的大小确定, ∠A的对边与邻边的比值不变。如果改变∠A 的大小, ∠A的对边与邻边的比值会随之改变吗? C2由此你得出什么结论?∠A的大小改变, ∠A的对边与邻边的比值随之改变。当直角三角形的锐角确定后,它的对边与邻边的比值也随之唯一确定;比值和三角形的大小无关,只和倾斜角的大小有关。B AB C∠A的对边∠A的邻边∠A的对边∠A的邻边tanA∠A的正切在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比随之确定,这个比叫做∠A的正切.记作:tanA读?思考 前面我们讨论了梯子的倾斜程度,梯子的倾斜程度与tanA有关系吗?tanA的值越大,梯子越陡.一,思考: 1.判断对错:
如图, tanA=
小试牛刀2、如图
(2) tanA= ( )
(3)tanA= ( )
(4)tanA=0.7m( )
(5) tanB= ( )
小试牛刀3、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A、扩大100倍 B、缩小100倍
C、不变 D、不能确定小试牛刀二. 填空:
1.tan =
tan =
2.如图, ∠ACB=90°CD⊥AB.
tan∠ACD=
tanB=
BAAC摩 拳 擦 掌tanA·tanB =______1定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2) tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
3) tanA﹥0 且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序: ).
4)tanA不表示“tan”乘以“A ”.
5) tanA的大小只与∠A的大小有关,而与直角三角形的边长无关定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2) tanA不表示“tan”乘以“A ”.它是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC.∠1的正切表示为:tan∠1.
3) tanA﹥0 且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意
顺序: ).
4) tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.行家看“门道”例1 下图表示两个自动扶梯,哪一个自动扶梯比较陡? 例题欣赏解:甲梯中,驶向胜利的彼岸乙梯中,∵tanβ>tanα,
∴乙梯更陡.老师提示:
生活中,常用一个锐角的正切表示梯子的倾斜程度.用数学去解释生活如图,正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:老师提示:
坡面与水平面的夹角称为坡角,坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切.驶向胜利的彼岸例2 如图,拦水坝的坡度i=1: ,若坝高
BC=20米,求坝面AB的长。达标反馈驶向胜利的彼岸相信自己是最棒的!回顾这节课你有哪些收获?通过这节课的学习,你想进一步探究的问题是什么?驶向胜利的彼岸 不管你是否愿意,数学将无处不在。
数学,就如一条伶俐的小狗,你若喜欢它,它就向你摇头摆尾,忠心相随;可是你若嫌弃它,疏远它,它就会向你狂吠,冷不防咬你一口!
望你乘上数学之舟,科学之箭,闯荡未来的人生。
再见挑战自己:(选做题)
(2008·泰安)直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是多少?
倾斜角越大——梯子陡 可以用梯子与地面的夹角(倾斜角)的大小来判断两架梯子哪个更陡些。 实例1:如图,梯子AB和EF哪个更陡?你是怎样判断的?还可以用梯子的顶端放在墙上位置的高低及梯子的底端离墙的远近来判断。 实例2:如图,梯子AB和EF哪个更陡?你是怎样判断的?梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 水平宽度铅直高度倾斜角在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知梯子在上升变陡过程中,铅直高度与水平宽度的比发生了什么变化? 在实践中探索新知 实例2:如图,梯子AB和EF哪个更陡?你是怎样判断的?梯子的铅直高与其水平距离的比相同时,梯子就一样陡。比值大的梯子陡。 若小明因身高原因不能顺利测量梯子顶端到墙脚的距离B1 C1 ,进而无法刻画梯子的倾斜程度,他该怎么办?你有什么锦囊妙计? AC1B1驶向胜利的彼岸请你想一想 AB1 C1 C2B2 如果改变B2在梯子上的位置呢?由此你能得出什么结论?由感性到理性请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2 AB1 C1 C2B2由感性到理性请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2 如果改变B2在梯子上的位置呢?由此你能得出什么结论? AB1 C1 C2B2请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2由感性到理性 如果改变B2在梯子上的位置呢?由此你能得出什么结论? AB1 C1 C2B2请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2由感性到理性 如果改变B2在梯子上的位置呢?由此你能得出什么结论? AB1 C1 C2B2请你想一想∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2 ∵B1C1⊥AC1, B2C2 ⊥ AC1
∴ ∠AC1B1=∠AC2B2由感性到理性 如果改变B2在梯子上的位置呢?由此你能得出什么结论?任意改变B2在梯子上的位置,则:∠A的大小确定, ∠A的对边与邻边的比值不变。如果改变∠A 的大小, ∠A的对边与邻边的比值会随之改变吗? C2由此你得出什么结论?∠A的大小改变, ∠A的对边与邻边的比值随之改变。当直角三角形的锐角确定后,它的对边与邻边的比值也随之唯一确定;比值和三角形的大小无关,只和倾斜角的大小有关。B AB C∠A的对边∠A的邻边∠A的对边∠A的邻边tanA∠A的正切在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比随之确定,这个比叫做∠A的正切.记作:tanA读?思考 前面我们讨论了梯子的倾斜程度,梯子的倾斜程度与tanA有关系吗?tanA的值越大,梯子越陡.一,思考: 1.判断对错:
如图, tanA=
小试牛刀2、如图
(2) tanA= ( )
(3)tanA= ( )
(4)tanA=0.7m( )
(5) tanB= ( )
小试牛刀3、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A、扩大100倍 B、缩小100倍
C、不变 D、不能确定小试牛刀二. 填空:
1.tan =
tan =
2.如图, ∠ACB=90°CD⊥AB.
tan∠ACD=
tanB=
BAAC摩 拳 擦 掌tanA·tanB =______1定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2) tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
3) tanA﹥0 且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序: ).
4)tanA不表示“tan”乘以“A ”.
5) tanA的大小只与∠A的大小有关,而与直角三角形的边长无关定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2) tanA不表示“tan”乘以“A ”.它是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC.∠1的正切表示为:tan∠1.
3) tanA﹥0 且没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意
顺序: ).
4) tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.行家看“门道”例1 下图表示两个自动扶梯,哪一个自动扶梯比较陡? 例题欣赏解:甲梯中,驶向胜利的彼岸乙梯中,∵tanβ>tanα,
∴乙梯更陡.老师提示:
生活中,常用一个锐角的正切表示梯子的倾斜程度.用数学去解释生活如图,正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:老师提示:
坡面与水平面的夹角称为坡角,坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切.驶向胜利的彼岸例2 如图,拦水坝的坡度i=1: ,若坝高
BC=20米,求坝面AB的长。达标反馈驶向胜利的彼岸相信自己是最棒的!回顾这节课你有哪些收获?通过这节课的学习,你想进一步探究的问题是什么?驶向胜利的彼岸 不管你是否愿意,数学将无处不在。
数学,就如一条伶俐的小狗,你若喜欢它,它就向你摇头摆尾,忠心相随;可是你若嫌弃它,疏远它,它就会向你狂吠,冷不防咬你一口!
望你乘上数学之舟,科学之箭,闯荡未来的人生。
再见挑战自己:(选做题)
(2008·泰安)直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是多少?
