六年级数学上册教案 圆的周长 1(冀教版)
文档属性
| 名称 | 六年级数学上册教案 圆的周长 1(冀教版) |  | |
| 格式 | rar | ||
| 文件大小 | 15.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-11-16 12:19:00 | ||
图片预览





文档简介
(共40张PPT)
动手试一试:
如图,丰台花园有一块三角形的土地,准备在这块土地上种上四种不同颜色的花,要求四种花所占的面积相等,请你们小组设计合理的解决方案。
动手试一试:
如图,丰台花园有一块三角形的土地,准备在这块土地上种上四种不同颜色的花,要求四种花所占的面积相等,请你们小组设计合理的解决方案。
动手试一试:
如图,丰台花园有一块三角形的土地,准备在这块土地上种上四种不同颜色的花,要求四种花所占的面积相等,请你们小组设计合理的解决方案。
面积相等
设计新要求:
形状相同
全等图形
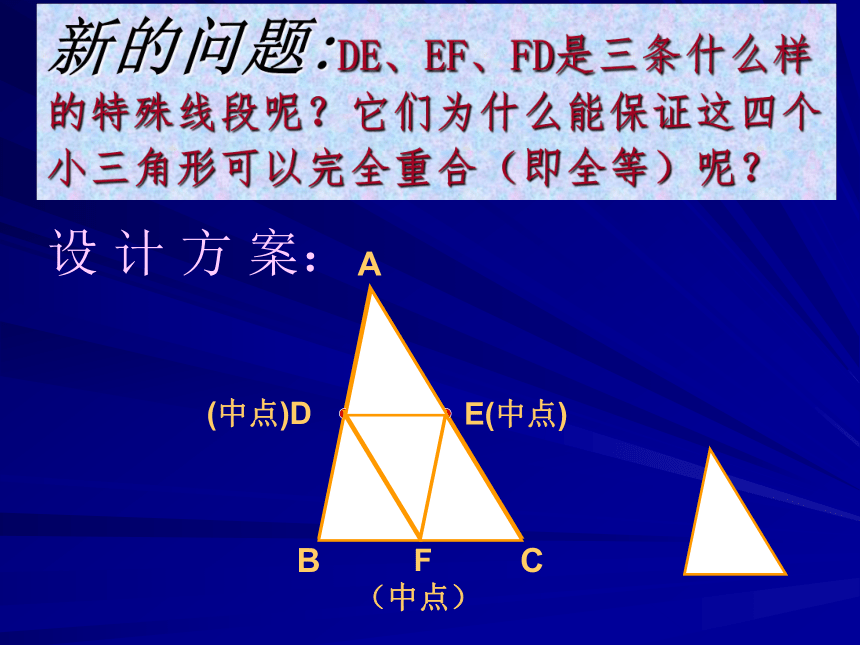
设 计 方 案:
F
(中点)
(中点)D
E(中点)
A
B
C
新的问题:DE、EF、FD是三条什么样的特殊线段呢?它们为什么能保证这四个小三角形可以完全重合(即全等)呢?
F
(中点)
(中点)D
E(中点)
A
B
C
F
(中点)
(中点)D
E(中点)
A
B
C
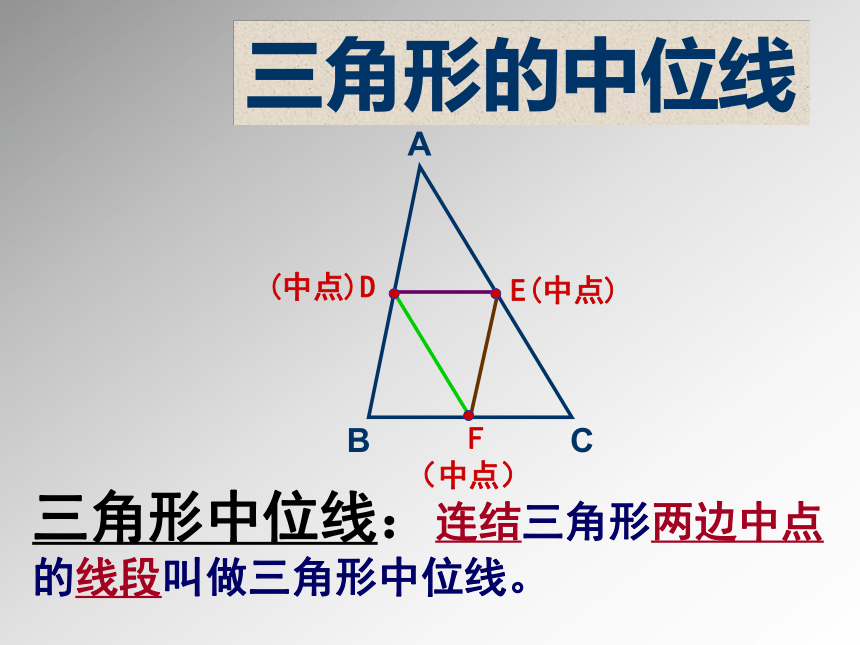
三角形的中位线
三角形中位线:连结三角形两边中点的线段叫做三角形中位线。
三角形的中位线
F
(中点)
(中点)D
E(中点)
A
B
C
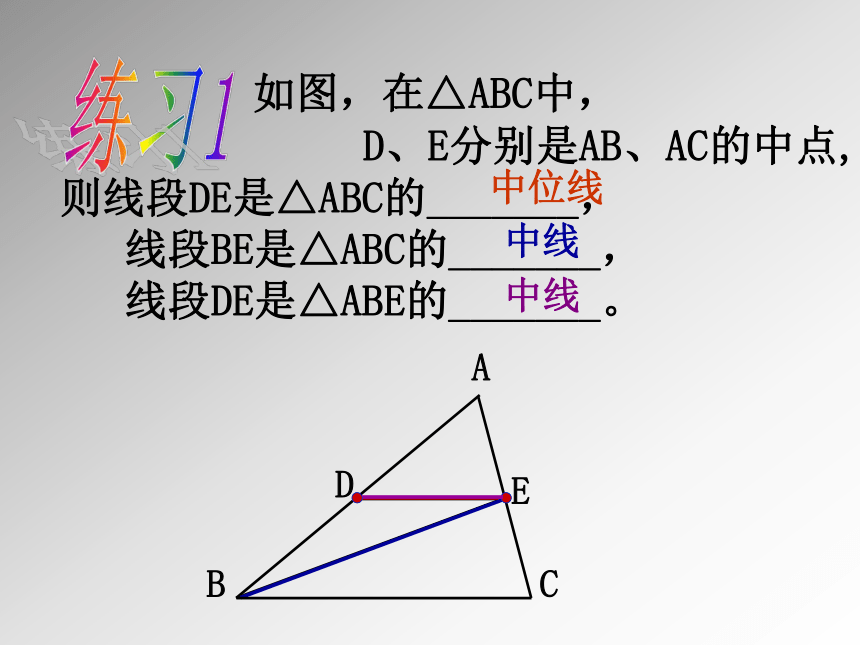
如图,在△ABC中,
D、E分别是AB、AC的中点,
则线段DE是△ABC的_______,
线段BE是△ABC的_______,
线段DE是△ABE的_______。
中位线
中线
中线
D
E
A
C
B
(1)相同之处——都和边的中点有关;
(2)不同之处:
三角形中位线的两个端点都是边的中点;
三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。
C
B
A
E
D
概念对比
C
B
A
D
中线DC
中位线DE
(中点)D
E(中点)
A
B
C
大胆猜一猜
三角形中位线有什么特殊的性质呢?
活动内容:
三角形中位线是三角形中的重要线段,请大家观察《几何画板》的课件,猜想三角形中位线的特征。
活动要求:
请各小组认真观察、积极思考,举手回答问题。
进入几何画板
友情提示
从如何构成平行四边形上去思考。
已知:如图,
DE是△ABC的中位线
求证:DE = BC
C
B
A
E
D
DE∥BC
∵ DE是△ABC的中位线
∴ ⑴ DE∥BC
⑵ DE = BC
三角形的中位线平行于第三边,并等于它的一半。
推理形式
数量关系
位置关系
(DE BC)
∥
=
C
B
A
E
D
已知:在△ABC中,AB、BC、AC的长分别为5cm、8cm和9cm,点D、点F、点E分别是AB、BC、AC的中点,连结DE、EF、FD,
(1)求△DEF的周长是______cm;
3
11
(2)变式练习:若△ABC的周长是a,△DEF的
周长是
(3)图中有______组平行线,
有______个平行四边形。
3
a
________ ;
C
B
A
E
D
F
提问:这两个小题用到了“三角形
中位线定理”的哪部分结论?
数量关系
已知:在△ABC中,AB、BC、AC的长分别为5cm、8cm和9cm,点D、点F、点E分别是AB、BC、AC的中点,连结DE、EF、FD,
(1)求△DEF的周长是______cm;
11
(2)变式练习:若△ABC的周长是a,△DEF的
周长是
a
________ ;
3
(3)图中有______组平行线,
有______个平行四边形。
3
C
B
A
E
D
F
提问:这两个小题用到了“三角形
中位线定理”的哪部分结论?
数量关系
因为图中的四边形ADFE、四边形DBFE、四边形DFCE都是平行四边形,因此可以很容易证明出所分割的四个三角形都是全等的。
问题解决
如图,AF = FD = DB,FG∥DE∥BC,
A
B
F
G
E
C
D
P
点F是线段AD的中点。
点D是线段EB的中点。
点G是线段AE的中点。
点E是线段GC的中点。
点P是线段FC的中点。
(1)请找出图中所有的中点;
(2)请找出图中所有的三角形中位线。
如图,AF = FD = DB,FG∥DE∥BC,
A
B
F
G
E
C
D
P
(1)请找出图中所有的中点;
点F是线段AD的中点。
点D是线段EB的中点。
点G是线段AE的中点。
点E是线段GC的中点。
点P是线段EC的中点。
(2)请找出图中所有的三角形中位线。
中位线FG
DE是三角形中位线吗?
中位线DP
中位线PE
如图,AF = FD = DB,FG∥DE∥BC,
A
B
F
G
E
C
D
P
(1)请找出图中所有的中点;
(2)请找出图中所有的三角形中位线。
(3)如果PE=1.5,你可以求出哪些线段的长度?
9
3
4.5
1.5
6
中位线FG
中位线DP
中位线PE
C
B
A
E(中点)
(中点)D
定理对比
C
B
A
(中点)D
E(中点)
三角形中位线定理
平行线等分线段定理推论2
(蓝色是已知,红色是结论)
中点 + ∥
中点 + 中点
中点
∥
求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形。
四边形EFGH是平行四边形。
A
D
C
B
E
F
G
H
在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
(文字证明题)
已知:
求证:
1、你学了哪些新知识?
三角形中位线的定义,
三角形中位线定理。
课堂小结
2、在这节课中,你所学习的新知识都和哪些旧知识做过比较?它们各自的区别是什么?
“三角形的中线”和“中位线”的对比。
“三角形中位线定理”与“平行线等分线段定理推论2”的对比。
课堂小结
3、在这节课中,你掌握了什么样的几何基本图形?
C
B
A
E
D
课堂小结
生活中处处有数学的影子,只要留心观察身边的事物,开动脑筋,就能从实际生活中发现许多的数学问题;同时通过学习这些数学知识,反过来又可以解决这类的生活实际问题。
数学活动:
请大家通过课件的演示完成“中点四边形”的相关练习。
已知:如图,△ABC中,D是AB中点,E是AC上的点,且AE = 2EC,CD、BE交于O点,
求证:OE = BE。
A
O
B
C
4
1
D
E
D
已知:如图,△ABC中,D是AB中点,E是AC上的点,且AE = 2EC,CD、BE交于O点,
求证:OE = BE。
A
O
B
C
4
1
D
E
D
F
分析:取AE中点F,连结DF
(3)OE = DF
2
1
( 1 )DF = BE
2
1
( 2 )F是AE的中点,AE = 2EC
∴ OE = BE
4
1
E是FC的中点
DF∥BE
O是DC的中点
构造三角形中位线定理条件,添加辅助线的关键:
提问:运用三角形中位线定理时,如何适当地添加辅助线
②有三角形而无中位线,要作中点的连线或过中点作平行线。
①有中点连线而无三角形,要作辅助线产生三角形;
C
B
A
E
D
C
B
A
E
D
动手试一试:
如图,丰台花园有一块三角形的土地,准备在这块土地上种上四种不同颜色的花,要求四种花所占的面积相等,请你们小组设计合理的解决方案。
动手试一试:
如图,丰台花园有一块三角形的土地,准备在这块土地上种上四种不同颜色的花,要求四种花所占的面积相等,请你们小组设计合理的解决方案。
动手试一试:
如图,丰台花园有一块三角形的土地,准备在这块土地上种上四种不同颜色的花,要求四种花所占的面积相等,请你们小组设计合理的解决方案。
面积相等
设计新要求:
形状相同
全等图形
设 计 方 案:
F
(中点)
(中点)D
E(中点)
A
B
C
新的问题:DE、EF、FD是三条什么样的特殊线段呢?它们为什么能保证这四个小三角形可以完全重合(即全等)呢?
F
(中点)
(中点)D
E(中点)
A
B
C
F
(中点)
(中点)D
E(中点)
A
B
C
三角形的中位线
三角形中位线:连结三角形两边中点的线段叫做三角形中位线。
三角形的中位线
F
(中点)
(中点)D
E(中点)
A
B
C
如图,在△ABC中,
D、E分别是AB、AC的中点,
则线段DE是△ABC的_______,
线段BE是△ABC的_______,
线段DE是△ABE的_______。
中位线
中线
中线
D
E
A
C
B
(1)相同之处——都和边的中点有关;
(2)不同之处:
三角形中位线的两个端点都是边的中点;
三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。
C
B
A
E
D
概念对比
C
B
A
D
中线DC
中位线DE
(中点)D
E(中点)
A
B
C
大胆猜一猜
三角形中位线有什么特殊的性质呢?
活动内容:
三角形中位线是三角形中的重要线段,请大家观察《几何画板》的课件,猜想三角形中位线的特征。
活动要求:
请各小组认真观察、积极思考,举手回答问题。
进入几何画板
友情提示
从如何构成平行四边形上去思考。
已知:如图,
DE是△ABC的中位线
求证:DE = BC
C
B
A
E
D
DE∥BC
∵ DE是△ABC的中位线
∴ ⑴ DE∥BC
⑵ DE = BC
三角形的中位线平行于第三边,并等于它的一半。
推理形式
数量关系
位置关系
(DE BC)
∥
=
C
B
A
E
D
已知:在△ABC中,AB、BC、AC的长分别为5cm、8cm和9cm,点D、点F、点E分别是AB、BC、AC的中点,连结DE、EF、FD,
(1)求△DEF的周长是______cm;
3
11
(2)变式练习:若△ABC的周长是a,△DEF的
周长是
(3)图中有______组平行线,
有______个平行四边形。
3
a
________ ;
C
B
A
E
D
F
提问:这两个小题用到了“三角形
中位线定理”的哪部分结论?
数量关系
已知:在△ABC中,AB、BC、AC的长分别为5cm、8cm和9cm,点D、点F、点E分别是AB、BC、AC的中点,连结DE、EF、FD,
(1)求△DEF的周长是______cm;
11
(2)变式练习:若△ABC的周长是a,△DEF的
周长是
a
________ ;
3
(3)图中有______组平行线,
有______个平行四边形。
3
C
B
A
E
D
F
提问:这两个小题用到了“三角形
中位线定理”的哪部分结论?
数量关系
因为图中的四边形ADFE、四边形DBFE、四边形DFCE都是平行四边形,因此可以很容易证明出所分割的四个三角形都是全等的。
问题解决
如图,AF = FD = DB,FG∥DE∥BC,
A
B
F
G
E
C
D
P
点F是线段AD的中点。
点D是线段EB的中点。
点G是线段AE的中点。
点E是线段GC的中点。
点P是线段FC的中点。
(1)请找出图中所有的中点;
(2)请找出图中所有的三角形中位线。
如图,AF = FD = DB,FG∥DE∥BC,
A
B
F
G
E
C
D
P
(1)请找出图中所有的中点;
点F是线段AD的中点。
点D是线段EB的中点。
点G是线段AE的中点。
点E是线段GC的中点。
点P是线段EC的中点。
(2)请找出图中所有的三角形中位线。
中位线FG
DE是三角形中位线吗?
中位线DP
中位线PE
如图,AF = FD = DB,FG∥DE∥BC,
A
B
F
G
E
C
D
P
(1)请找出图中所有的中点;
(2)请找出图中所有的三角形中位线。
(3)如果PE=1.5,你可以求出哪些线段的长度?
9
3
4.5
1.5
6
中位线FG
中位线DP
中位线PE
C
B
A
E(中点)
(中点)D
定理对比
C
B
A
(中点)D
E(中点)
三角形中位线定理
平行线等分线段定理推论2
(蓝色是已知,红色是结论)
中点 + ∥
中点 + 中点
中点
∥
求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形。
四边形EFGH是平行四边形。
A
D
C
B
E
F
G
H
在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
(文字证明题)
已知:
求证:
1、你学了哪些新知识?
三角形中位线的定义,
三角形中位线定理。
课堂小结
2、在这节课中,你所学习的新知识都和哪些旧知识做过比较?它们各自的区别是什么?
“三角形的中线”和“中位线”的对比。
“三角形中位线定理”与“平行线等分线段定理推论2”的对比。
课堂小结
3、在这节课中,你掌握了什么样的几何基本图形?
C
B
A
E
D
课堂小结
生活中处处有数学的影子,只要留心观察身边的事物,开动脑筋,就能从实际生活中发现许多的数学问题;同时通过学习这些数学知识,反过来又可以解决这类的生活实际问题。
数学活动:
请大家通过课件的演示完成“中点四边形”的相关练习。
已知:如图,△ABC中,D是AB中点,E是AC上的点,且AE = 2EC,CD、BE交于O点,
求证:OE = BE。
A
O
B
C
4
1
D
E
D
已知:如图,△ABC中,D是AB中点,E是AC上的点,且AE = 2EC,CD、BE交于O点,
求证:OE = BE。
A
O
B
C
4
1
D
E
D
F
分析:取AE中点F,连结DF
(3)OE = DF
2
1
( 1 )DF = BE
2
1
( 2 )F是AE的中点,AE = 2EC
∴ OE = BE
4
1
E是FC的中点
DF∥BE
O是DC的中点
构造三角形中位线定理条件,添加辅助线的关键:
提问:运用三角形中位线定理时,如何适当地添加辅助线
②有三角形而无中位线,要作中点的连线或过中点作平行线。
①有中点连线而无三角形,要作辅助线产生三角形;
C
B
A
E
D
C
B
A
E
D
