云南省蒙自市蒙自第一中学2015-2016学年高二下学期开学考试数学(理)试题
文档属性
| 名称 | 云南省蒙自市蒙自第一中学2015-2016学年高二下学期开学考试数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 923.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-14 18:12:54 | ||
图片预览



文档简介
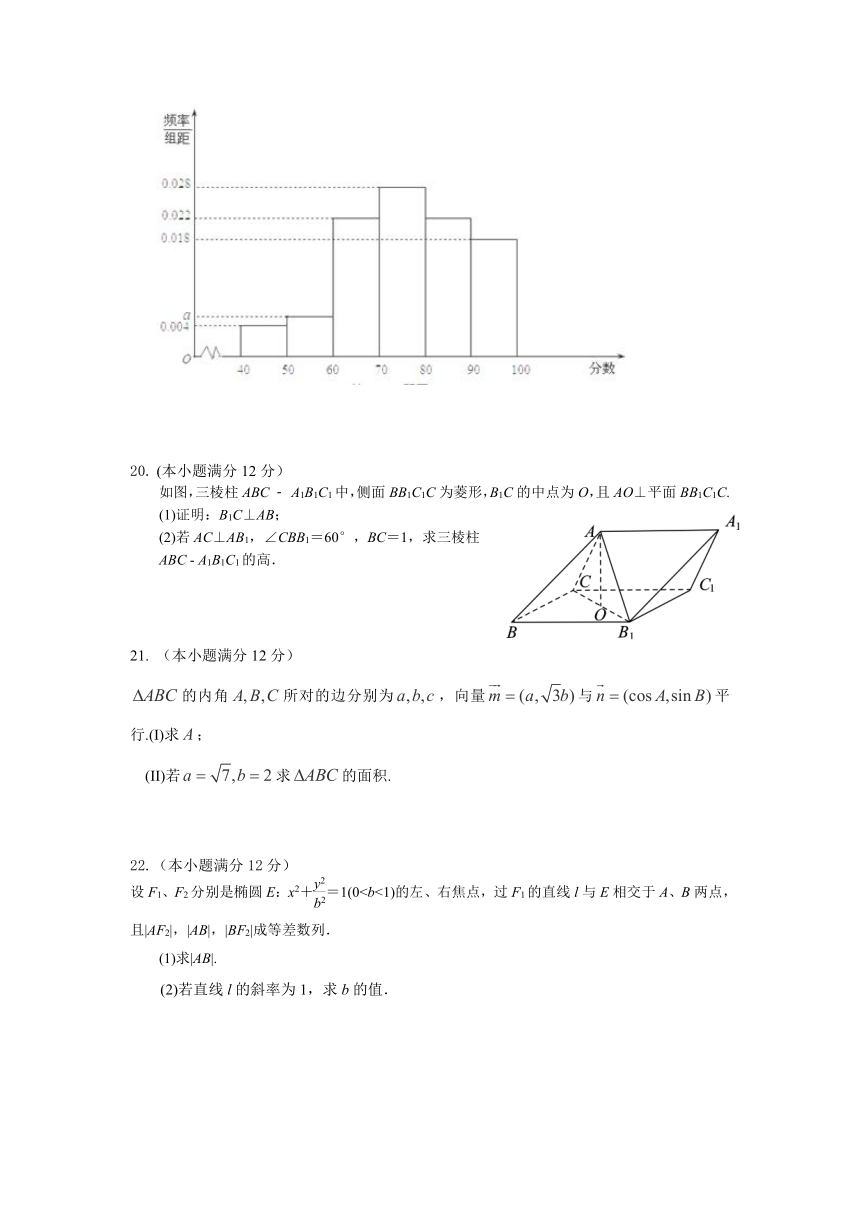
蒙自一中2015--2016学年下学期入学考试卷
高二数学试卷
本试卷分第I卷和第II卷两部分.考试时间:120分钟 满分:150分21世纪教育网
第Ⅰ卷(选择题)
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、已知集合A=,B=则AB=( )
A B C D
2、设,是两个不同的平面,是直线且.“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3、已知命题p:对任意x∈R,总有2x>0;q:“x>1”是“x>2”的充分不必要条件,
则下列命题为真命题的是( )
A.p∧q B. p∧ q
C. p∧q D.p∧ q
4、.若某几何体的三视图如下图所示,则此几何体的体积等于( )
A. B.
C. D.
5、执行如右图所示的的程序框图,若输入的x的值为1,则输出的n的值为________.
A.6 B.5 C.4 D.3
6、若直线与圆相交于A,B两点,且(O为坐标原点),则=_____.
A.1 B.2 C. D.3
7、若函数有两个零点,则实数的取值范围是_____.
A. B. C. D.
8、已知等差数列{an}的前n项和为S,a5=5,S5=15,则数列{}的前100项和为( )
A. B. C. D.
9、若非零向量a,b满足|a|=|b|,且(a-b)(3a+2b),则a与b的夹角为 ( )
A、 B、 C、 D、
10、已知,满足约束条件 ( http: / / www.21cnjy.com ),若的最小值为,则( )
A. B. C. D.
11、已知、取值如下表:
0 1 4 5 6
1.3 5.6 7.4
画散点图分析可知:与线性相关,且求得回归方程为,则的值(精确到0.1)为( )
A.1.5 B.1.6 C.1.7 D.1.8
12.双曲线﹣=1(a>0,b>0)的两个焦点为F1,F2,若P为其图象上一点,且|PF1|=3|PF2|,则该双曲线离心率的取值范围为( )
A.(1,2] B.(1,2) C.(2,) D.[2,)
第Ⅱ卷(非选择题)
二、填空题:(本大题共4小题,每小题5分,共20分.)
13、如图,在边长为1的正方形OABC中任取一点P,分别以O,B
为圆心,半径为画圆弧,点P在两圆之外的概率为 .
14、过抛物线y2=4x的焦点作直线交抛 ( http: / / www.21cnjy.com )物线于A(x1,y1)、B(x2,y2)两点,若x1+x2=10,则弦AB的长度为
15、设函数f(x)=是R上的单调递减函数,则实数a的取值范围为( )
16、已知α,β为锐角,且cos(α+β)=sin(α-β),则tanα=________.
三、解答题:(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分10分)
已知P={x|a-418.(本小题满分12分)
在公差不为零的等差数列{an}和等比数列{bn}中,已知a1=b1=1,a2=b2,,
(1)求等差数列{an}的通项公式an和等比数列{bn}的通项公式bn;
(2)求数列{an·bn}的前n项和Sn.
19. (本小题满分12分)
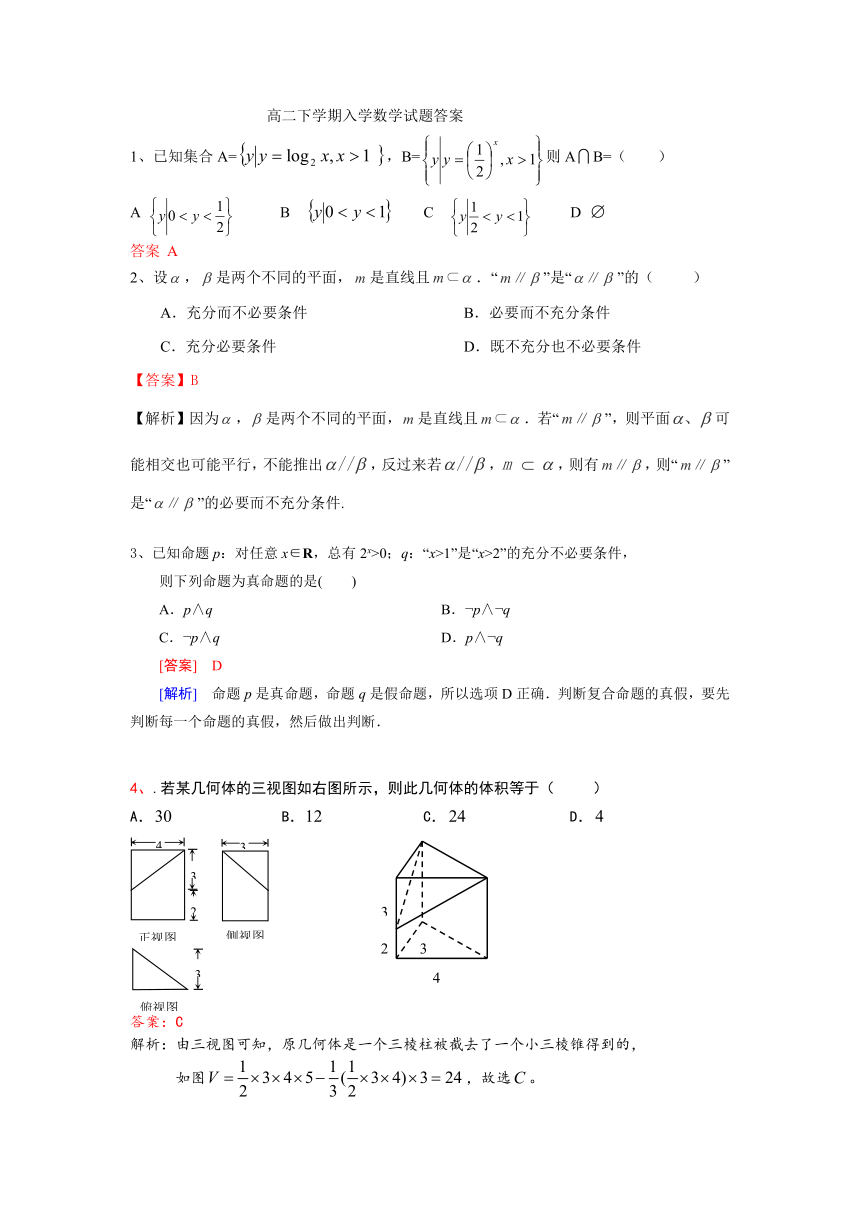
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
(Ⅰ)求频率分布图中的值;
(Ⅱ)估计该企业的职工对该部门评分不低于80的概率;
(Ⅲ)从评分在的受访职工中,随机抽取2人,求此2人评分都在的概率.
20. (本小题满分12分)
如图,三棱柱ABC A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.
(1)证明:B1C⊥AB;
(2)若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱
ABC A1B1C1的高.
21. (本小题满分12分)
的内角所对的边分别为,向量与平行.(I)求;
(II)若求的面积.
22.(本小题满分12分)
设F1、F2分别是椭圆E:x2+=1(0(1)求|AB|.
(2)若直线l的斜率为1,求b的值.
高二下学期入学数学试题答案
1、已知集合A=,B=则AB=( )
A B C D
答案 A
2、设,是两个不同的平面,是直线且.“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】B
【解析】因为,是两个不同的平面,是直线且.若“”,则平面可能相交也可能平行,不能推出,反过来若,,则有,则“”是“”的必要而不充分条件.
3、已知命题p:对任意x∈R,总有2x>0;q:“x>1”是“x>2”的充分不必要条件,
则下列命题为真命题的是( )
A.p∧q B. p∧ q
C. p∧q D.p∧ q
[答案] D
[解析] 命题p是真命题,命题q是假命题,所以选项D正确.判断复合命题的真假,要先判断每一个命题的真假,然后做出判断.
4、.若某几何体的三视图如右图所示,则此几何体的体积等于( )
A. B. C. D.
答案:C
解析:由三视图可知,原几何体是一个三棱柱被截去了一个小三棱锥得到的,
如图,故选。
5、执行如图所示的的程序框图,若输入的x的值为1,则输出的n的值为________.
11.3 [解析] x=1满足不等式,执行 ( http: / / www.21cnjy.com )循环后x=2,n=1;x=2满足不等式,执行循环后得x=3,n=2;x=3满足不等式,执行循环后得x=4,n=3.x=4不满足不等式,结束循环,输出n=3.
A.6 B.5 C.4 D.3
答案D
6、若直线与圆相交于A,B两点,且(O为坐标原点),则=_____.
A.1 B.2 C. D.3
【解析】如图直线与圆 交于A、B两点,O为坐标原点,且,则圆心(0,0)到直线的距离为 , .故答案为B
7、若函数有两个零点,则实数的取值范围是_____.
A. B. C. D.
【解析】由函数有两个零点,可得有两个不等的根,从而可得函数函数的图象有两个交点,结合函数的图象可得,,故答案为:D.
( http: / / www.21cnjy.com )
【考点定位】函数零点
【名师点睛】已知函数有零点(方程有根)求参数取值范围常用的方法
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围.
(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决.
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图像,然后数形结合求解.
8、已知等差数列{an}的前n项和为S,a5=5,S5=15,则数列{}的前100项和为( )
A. B.
C. D.
答案 A
9、若非零向量a,b满足|a|=|b|,且(a-b)(3a+2b),则a与b的夹角为 ( )
A、 B、 C、 D、
【答案】A
( http: / / www.21cnjy.com )
10、已知,满足约束条件 ( http: / / www.21cnjy.com ),若的最小值为,则( )
A. B. C. D.
答案:B
解析:依题意可以画出不等式表示的图形,当过点时取最小值,即2-2=1,=。
11、已知、取值如下表:
0 1 4 5 6
1.3 5.6 7.4
画散点图分析可知:与线性相关,且求得回归方程为,则的值(精确到0.1)为( )
A.1.5 B.1.6 C.1.7 D.1.8
答案:C
解析:将代入回归方程为可得,则,解得,即精确到0.1后的值为. 故选C。
12.双曲线﹣=1(a>0,b>0)的两个焦点为F1,F2,若P为其图象上一点,且|PF1|=3|PF2|,则该双曲线离心率的取值范围为( )
A.(1,2] B.(1,2) C.(2,+∞) D.[2,+∞)
【考点】双曲线的简单性质.
【专题】计算题;圆锥曲线的定义、性质与方程.
【分析】先根据双曲线定义可知|PF1|﹣| ( http: / / www.21cnjy.com )PF2|=2a,进而根据|PF1|=3|PF2|,求得a=|PF2|,同时利用三角形中两边之和大于第三边的性质,推断出,|F1F2|<|PF1|+|PF2|,进而求得a和c的不等式关系,分析当p为双曲线顶点时,e=2且双曲线离心率大于1,最后综合答案可得.
【解答】解:根据双曲线定义可知|PF1|﹣|PF2|=2a,
即3|PF2|﹣|PF2|=2a,
∴a=|PF2|,|PF1|=3a,
在△PF1F2中,|F1F2|<|PF1|+|PF2|,
2c<4|PF2|,c<2|PF2|=2a,
∴<2,
当P为双曲线顶点时, =2,
又∵双曲线e>1,
∴1<e≤2
故选:A.
二、填空题
13、如图,在边长为1的正方形OABC中任取一点P,分别以O,B为圆心,半径为画圆弧,点P在两圆之外的概率为 .
【解析】依题设知所求概率
答案:1-
14、过抛物线y2=4x的 ( http: / / www.21cnjy.com )焦点作直线交抛物线于A(x1,y1)、B(x2,y2)两点,若x1+x2=10,则弦AB的长度为
[解析] 设抛物线的焦点为F,则|AB|=|AF|+|BF|=x1+1+x2+1=x1+x2+2=10+2=12.
15、设函数f(x)=是R上的单调递减函数,则实数a的取值范围为( )
[解析] 依题意可得解得a≤.
16、已知α,β为锐角,且cos(α+β)=sin(α-β),则tanα=________.
解析:∵cos(α+β)=sin(α-β),
∴cosαcosβ-sinαsinβ=sinαcosβ-cosαsinβ.
∴cosα(sinβ+cosβ)=sinα(sinβ+cosβ).
∵β为锐角,∴sinβ+cosβ≠0,∴cosα=sinα,
∴tanα=1.
三、解答题
17、已知P={x|a-4[解析] P={x|a-4∵x∈P是x∈Q的必要条件
∴x∈Q x∈P,即Q P
∴
∴-1≤a≤5.
18、在公差不为零的等差数列{an}和等比数列{bn}中,已知a1=b1=1,a2=b2,
(1)求等差数列{an}的通项公式an和等比数列{bn}的通项公式bn;
(2)求数列{an·bn}的前n项和Sn.
解:(1)设公差为d(d≠0),公比为q.由已知得
∴an=3n-2,bn=4n-1.
(2)由(1)可知an·bn=(3n-2)·4n-1,
∴Sn=1+4×4+7×42+…+(3n-2)·4n-1, ①
4Sn=4+4×42+7×43+…+(3n-2)·4n. ②
由①-②得
-3Sn=1+3×4+3×42+3×4 ( http: / / www.21cnjy.com )3+…+3·4n-1-(3n-2)·4n=1+3×-(3n-2)·4n=1+4n-4-(3n-2)·4n=-3-3(n-1)·4n,
∴Sn=1+(n-1)·4n(n∈N*).
19、某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
(Ⅰ)求频率分布图中的值;
(Ⅱ)估计该企业的职工对该部门评分不低于80的概率;
(Ⅲ)从评分在的受访职工中,随机抽取2人,求此2人评分都在的概率.
( http: / / www.21cnjy.com )
【答案】(Ⅰ)0.006;(Ⅱ);(Ⅲ)
【解析】
(Ⅰ)因为,所以
(Ⅱ)由所给频率分布直方图知,50名受访职工评分不低于80的频率为,
所以该企业职工对该部门评分不低于80的概率的估计值为.
(Ⅲ)受访职工评分在[50,60)的有:50×0.006×10=3(人),即为;
受访职工评分在[40,50)的有: 50×0.004×10=2(人),即为.
从这5名受访职工中随机抽取2人,所有可能的结果共有10种,它们是
又因为所抽取2人的评分都在[40,50)的结果有1种,即,故所求的概率为.
20、如图,三棱柱ABC A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.
(1)证明:B1C⊥AB;
(2)若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱ABC A1B1C1的高.
解:(1)证明:连接BC1,则O为B1C与BC1的交点.
因为侧面BB1C1C为菱形,所以B1C⊥BC1.
又AO⊥平面BB1C1C,所以B1C⊥AO,
由于BC1∩AO=O,故B1C⊥平面ABO.
由于AB 平面ABO,故B1C⊥AB.
(2)作OD⊥BC,垂足为D,连接AD.作OH⊥AD,垂足为H.
由于BC⊥AO,BC⊥OD,且AO∩OD=O,
故BC⊥平面AOD,所以OH⊥BC.
又OH⊥AD,且AD∩BC=D,
所以OH⊥平面ABC.
因为∠CBB1=60°,所以△CBB1为等边三角形,又BC=1,可得OD=.
因为AC⊥AB1,所以OA=B1C=.
由OH·AD=OD·OA,且AD==,得OH=.
又O为B1C的中点,所以点B1到平面ABC的距离为.故三棱柱ABC A1B1C1的高为.
21、的内角所对的边分别为,向量与平行.
(I)求;
(II)若求的面积.
【答案】(I) ;(II) .
【解析】
试题分析: (I)因为,所以,由正弦定理,得,
又,从而,由于,所以;
(II)解法一:由余弦定理,得,代入数值求得,由面积公式得面积为.解法二:由正弦定理,得,从而,又由知,所以,由,计算得,所以面积为.
试题解析:(I)因为,所以
由正弦定理,得,
又,从而,
由于
所以
(II)解法一:由余弦定理,得
,而,,
得,即
因为,所以,
故面积为.
解法二:由正弦定理,得
从而
又由知,所以
故
,
所以面积为.
22、设F1、F2分别是椭圆E:x ( http: / / www.21cnjy.com )2+=1(0(1)求|AB|.
(2)若直线l的斜率为1,求b的值.
[解析] (1)求椭圆定义知|AF2|+|AB|+|BF2|=4,
又2|AB|=|AF2|+|BF2|,得|AB|=.
(2)l的方程式为y=x+c,其中c=,
设A(x1,y1),B(x1,y1),则A、B两点坐标满足方程组
消去y化简得(1+b2)x2+2cx+1-2b2=0.
则x1+x2=,x1x2=.
因为直线AB的斜率为1,所以|AB|=|x2-x1|,
即=|x2-x1|.
则=(x1+x2)2-4x1x2
=-=,
解得b=.
3
2
4
3
4
3
2
3
3
正视图
侧视图
俯视图
3
2
4
3
4
3
2
3
3
正视图
侧视图
俯视图
高二数学试卷
本试卷分第I卷和第II卷两部分.考试时间:120分钟 满分:150分21世纪教育网
第Ⅰ卷(选择题)
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、已知集合A=,B=则AB=( )
A B C D
2、设,是两个不同的平面,是直线且.“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3、已知命题p:对任意x∈R,总有2x>0;q:“x>1”是“x>2”的充分不必要条件,
则下列命题为真命题的是( )
A.p∧q B. p∧ q
C. p∧q D.p∧ q
4、.若某几何体的三视图如下图所示,则此几何体的体积等于( )
A. B.
C. D.
5、执行如右图所示的的程序框图,若输入的x的值为1,则输出的n的值为________.
A.6 B.5 C.4 D.3
6、若直线与圆相交于A,B两点,且(O为坐标原点),则=_____.
A.1 B.2 C. D.3
7、若函数有两个零点,则实数的取值范围是_____.
A. B. C. D.
8、已知等差数列{an}的前n项和为S,a5=5,S5=15,则数列{}的前100项和为( )
A. B. C. D.
9、若非零向量a,b满足|a|=|b|,且(a-b)(3a+2b),则a与b的夹角为 ( )
A、 B、 C、 D、
10、已知,满足约束条件 ( http: / / www.21cnjy.com ),若的最小值为,则( )
A. B. C. D.
11、已知、取值如下表:
0 1 4 5 6
1.3 5.6 7.4
画散点图分析可知:与线性相关,且求得回归方程为,则的值(精确到0.1)为( )
A.1.5 B.1.6 C.1.7 D.1.8
12.双曲线﹣=1(a>0,b>0)的两个焦点为F1,F2,若P为其图象上一点,且|PF1|=3|PF2|,则该双曲线离心率的取值范围为( )
A.(1,2] B.(1,2) C.(2,) D.[2,)
第Ⅱ卷(非选择题)
二、填空题:(本大题共4小题,每小题5分,共20分.)
13、如图,在边长为1的正方形OABC中任取一点P,分别以O,B
为圆心,半径为画圆弧,点P在两圆之外的概率为 .
14、过抛物线y2=4x的焦点作直线交抛 ( http: / / www.21cnjy.com )物线于A(x1,y1)、B(x2,y2)两点,若x1+x2=10,则弦AB的长度为
15、设函数f(x)=是R上的单调递减函数,则实数a的取值范围为( )
16、已知α,β为锐角,且cos(α+β)=sin(α-β),则tanα=________.
三、解答题:(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分10分)
已知P={x|a-4
在公差不为零的等差数列{an}和等比数列{bn}中,已知a1=b1=1,a2=b2,,
(1)求等差数列{an}的通项公式an和等比数列{bn}的通项公式bn;
(2)求数列{an·bn}的前n项和Sn.
19. (本小题满分12分)
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
(Ⅰ)求频率分布图中的值;
(Ⅱ)估计该企业的职工对该部门评分不低于80的概率;
(Ⅲ)从评分在的受访职工中,随机抽取2人,求此2人评分都在的概率.
20. (本小题满分12分)
如图,三棱柱ABC A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.
(1)证明:B1C⊥AB;
(2)若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱
ABC A1B1C1的高.
21. (本小题满分12分)
的内角所对的边分别为,向量与平行.(I)求;
(II)若求的面积.
22.(本小题满分12分)
设F1、F2分别是椭圆E:x2+=1(0
(2)若直线l的斜率为1,求b的值.
高二下学期入学数学试题答案
1、已知集合A=,B=则AB=( )
A B C D
答案 A
2、设,是两个不同的平面,是直线且.“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】B
【解析】因为,是两个不同的平面,是直线且.若“”,则平面可能相交也可能平行,不能推出,反过来若,,则有,则“”是“”的必要而不充分条件.
3、已知命题p:对任意x∈R,总有2x>0;q:“x>1”是“x>2”的充分不必要条件,
则下列命题为真命题的是( )
A.p∧q B. p∧ q
C. p∧q D.p∧ q
[答案] D
[解析] 命题p是真命题,命题q是假命题,所以选项D正确.判断复合命题的真假,要先判断每一个命题的真假,然后做出判断.
4、.若某几何体的三视图如右图所示,则此几何体的体积等于( )
A. B. C. D.
答案:C
解析:由三视图可知,原几何体是一个三棱柱被截去了一个小三棱锥得到的,
如图,故选。
5、执行如图所示的的程序框图,若输入的x的值为1,则输出的n的值为________.
11.3 [解析] x=1满足不等式,执行 ( http: / / www.21cnjy.com )循环后x=2,n=1;x=2满足不等式,执行循环后得x=3,n=2;x=3满足不等式,执行循环后得x=4,n=3.x=4不满足不等式,结束循环,输出n=3.
A.6 B.5 C.4 D.3
答案D
6、若直线与圆相交于A,B两点,且(O为坐标原点),则=_____.
A.1 B.2 C. D.3
【解析】如图直线与圆 交于A、B两点,O为坐标原点,且,则圆心(0,0)到直线的距离为 , .故答案为B
7、若函数有两个零点,则实数的取值范围是_____.
A. B. C. D.
【解析】由函数有两个零点,可得有两个不等的根,从而可得函数函数的图象有两个交点,结合函数的图象可得,,故答案为:D.
( http: / / www.21cnjy.com )
【考点定位】函数零点
【名师点睛】已知函数有零点(方程有根)求参数取值范围常用的方法
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围.
(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决.
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图像,然后数形结合求解.
8、已知等差数列{an}的前n项和为S,a5=5,S5=15,则数列{}的前100项和为( )
A. B.
C. D.
答案 A
9、若非零向量a,b满足|a|=|b|,且(a-b)(3a+2b),则a与b的夹角为 ( )
A、 B、 C、 D、
【答案】A
( http: / / www.21cnjy.com )
10、已知,满足约束条件 ( http: / / www.21cnjy.com ),若的最小值为,则( )
A. B. C. D.
答案:B
解析:依题意可以画出不等式表示的图形,当过点时取最小值,即2-2=1,=。
11、已知、取值如下表:
0 1 4 5 6
1.3 5.6 7.4
画散点图分析可知:与线性相关,且求得回归方程为,则的值(精确到0.1)为( )
A.1.5 B.1.6 C.1.7 D.1.8
答案:C
解析:将代入回归方程为可得,则,解得,即精确到0.1后的值为. 故选C。
12.双曲线﹣=1(a>0,b>0)的两个焦点为F1,F2,若P为其图象上一点,且|PF1|=3|PF2|,则该双曲线离心率的取值范围为( )
A.(1,2] B.(1,2) C.(2,+∞) D.[2,+∞)
【考点】双曲线的简单性质.
【专题】计算题;圆锥曲线的定义、性质与方程.
【分析】先根据双曲线定义可知|PF1|﹣| ( http: / / www.21cnjy.com )PF2|=2a,进而根据|PF1|=3|PF2|,求得a=|PF2|,同时利用三角形中两边之和大于第三边的性质,推断出,|F1F2|<|PF1|+|PF2|,进而求得a和c的不等式关系,分析当p为双曲线顶点时,e=2且双曲线离心率大于1,最后综合答案可得.
【解答】解:根据双曲线定义可知|PF1|﹣|PF2|=2a,
即3|PF2|﹣|PF2|=2a,
∴a=|PF2|,|PF1|=3a,
在△PF1F2中,|F1F2|<|PF1|+|PF2|,
2c<4|PF2|,c<2|PF2|=2a,
∴<2,
当P为双曲线顶点时, =2,
又∵双曲线e>1,
∴1<e≤2
故选:A.
二、填空题
13、如图,在边长为1的正方形OABC中任取一点P,分别以O,B为圆心,半径为画圆弧,点P在两圆之外的概率为 .
【解析】依题设知所求概率
答案:1-
14、过抛物线y2=4x的 ( http: / / www.21cnjy.com )焦点作直线交抛物线于A(x1,y1)、B(x2,y2)两点,若x1+x2=10,则弦AB的长度为
[解析] 设抛物线的焦点为F,则|AB|=|AF|+|BF|=x1+1+x2+1=x1+x2+2=10+2=12.
15、设函数f(x)=是R上的单调递减函数,则实数a的取值范围为( )
[解析] 依题意可得解得a≤.
16、已知α,β为锐角,且cos(α+β)=sin(α-β),则tanα=________.
解析:∵cos(α+β)=sin(α-β),
∴cosαcosβ-sinαsinβ=sinαcosβ-cosαsinβ.
∴cosα(sinβ+cosβ)=sinα(sinβ+cosβ).
∵β为锐角,∴sinβ+cosβ≠0,∴cosα=sinα,
∴tanα=1.
三、解答题
17、已知P={x|a-4
∴x∈Q x∈P,即Q P
∴
∴-1≤a≤5.
18、在公差不为零的等差数列{an}和等比数列{bn}中,已知a1=b1=1,a2=b2,
(1)求等差数列{an}的通项公式an和等比数列{bn}的通项公式bn;
(2)求数列{an·bn}的前n项和Sn.
解:(1)设公差为d(d≠0),公比为q.由已知得
∴an=3n-2,bn=4n-1.
(2)由(1)可知an·bn=(3n-2)·4n-1,
∴Sn=1+4×4+7×42+…+(3n-2)·4n-1, ①
4Sn=4+4×42+7×43+…+(3n-2)·4n. ②
由①-②得
-3Sn=1+3×4+3×42+3×4 ( http: / / www.21cnjy.com )3+…+3·4n-1-(3n-2)·4n=1+3×-(3n-2)·4n=1+4n-4-(3n-2)·4n=-3-3(n-1)·4n,
∴Sn=1+(n-1)·4n(n∈N*).
19、某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
(Ⅰ)求频率分布图中的值;
(Ⅱ)估计该企业的职工对该部门评分不低于80的概率;
(Ⅲ)从评分在的受访职工中,随机抽取2人,求此2人评分都在的概率.
( http: / / www.21cnjy.com )
【答案】(Ⅰ)0.006;(Ⅱ);(Ⅲ)
【解析】
(Ⅰ)因为,所以
(Ⅱ)由所给频率分布直方图知,50名受访职工评分不低于80的频率为,
所以该企业职工对该部门评分不低于80的概率的估计值为.
(Ⅲ)受访职工评分在[50,60)的有:50×0.006×10=3(人),即为;
受访职工评分在[40,50)的有: 50×0.004×10=2(人),即为.
从这5名受访职工中随机抽取2人,所有可能的结果共有10种,它们是
又因为所抽取2人的评分都在[40,50)的结果有1种,即,故所求的概率为.
20、如图,三棱柱ABC A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.
(1)证明:B1C⊥AB;
(2)若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱ABC A1B1C1的高.
解:(1)证明:连接BC1,则O为B1C与BC1的交点.
因为侧面BB1C1C为菱形,所以B1C⊥BC1.
又AO⊥平面BB1C1C,所以B1C⊥AO,
由于BC1∩AO=O,故B1C⊥平面ABO.
由于AB 平面ABO,故B1C⊥AB.
(2)作OD⊥BC,垂足为D,连接AD.作OH⊥AD,垂足为H.
由于BC⊥AO,BC⊥OD,且AO∩OD=O,
故BC⊥平面AOD,所以OH⊥BC.
又OH⊥AD,且AD∩BC=D,
所以OH⊥平面ABC.
因为∠CBB1=60°,所以△CBB1为等边三角形,又BC=1,可得OD=.
因为AC⊥AB1,所以OA=B1C=.
由OH·AD=OD·OA,且AD==,得OH=.
又O为B1C的中点,所以点B1到平面ABC的距离为.故三棱柱ABC A1B1C1的高为.
21、的内角所对的边分别为,向量与平行.
(I)求;
(II)若求的面积.
【答案】(I) ;(II) .
【解析】
试题分析: (I)因为,所以,由正弦定理,得,
又,从而,由于,所以;
(II)解法一:由余弦定理,得,代入数值求得,由面积公式得面积为.解法二:由正弦定理,得,从而,又由知,所以,由,计算得,所以面积为.
试题解析:(I)因为,所以
由正弦定理,得,
又,从而,
由于
所以
(II)解法一:由余弦定理,得
,而,,
得,即
因为,所以,
故面积为.
解法二:由正弦定理,得
从而
又由知,所以
故
,
所以面积为.
22、设F1、F2分别是椭圆E:x ( http: / / www.21cnjy.com )2+=1(0
(2)若直线l的斜率为1,求b的值.
[解析] (1)求椭圆定义知|AF2|+|AB|+|BF2|=4,
又2|AB|=|AF2|+|BF2|,得|AB|=.
(2)l的方程式为y=x+c,其中c=,
设A(x1,y1),B(x1,y1),则A、B两点坐标满足方程组
消去y化简得(1+b2)x2+2cx+1-2b2=0.
则x1+x2=,x1x2=.
因为直线AB的斜率为1,所以|AB|=|x2-x1|,
即=|x2-x1|.
则=(x1+x2)2-4x1x2
=-=,
解得b=.
3
2
4
3
4
3
2
3
3
正视图
侧视图
俯视图
3
2
4
3
4
3
2
3
3
正视图
侧视图
俯视图
同课章节目录
