9.9 利用位似放缩图形(第一课时) 课件评比
文档属性
| 名称 | 9.9 利用位似放缩图形(第一课时) 课件评比 |

|
|
| 格式 | pptx | ||
| 文件大小 | 29.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-06 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
9.9 利用位似放缩图形(第一课时)
鲁教版8年级下册 第9章 图形的相似
学习目标
1、理解图形的位似概念,掌握图形位似的性质。
2、会利用作位似图形的方法把一个图形进行放大或缩小。
3、经历位似图形性质的探索过程,发展学生的探究、交流能力,培养学生数学结合思想。
理解定义
应用定义
掌握方法
课堂实施
新知探究
概念学习
概念应用
课堂小结
作业布置
手机屏幕
放大镜
大屏幕
新知引入
问题提出
问题辨析
深入探究
新知探究
利用位似放缩图形
从生活实例中抽象出数学模型
问题1: 和 的对应边有怎样的位置关系 和数量关系?
新知引入
课堂实施
新知探究
概念学习
概念应用
课堂小结
作业布置
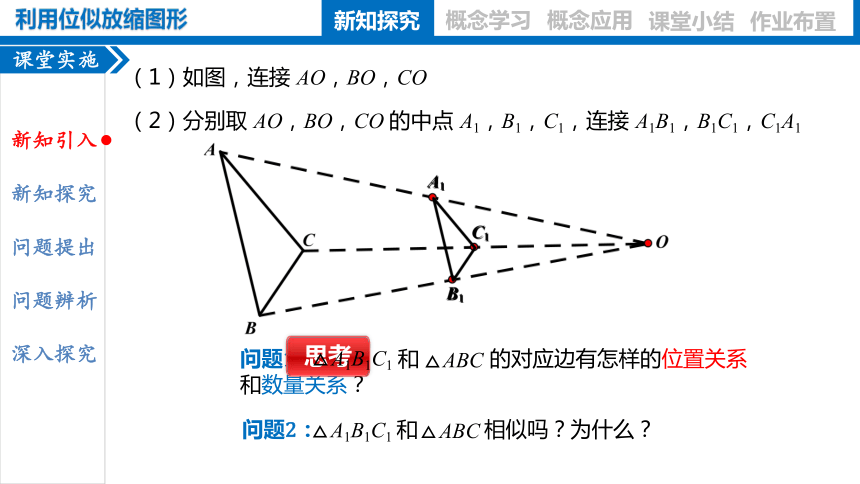
(1)如图,连接 AO,BO,CO
(2)分别取 AO,BO,CO 的中点 A1,B1,C1,连接 A1B1,B1C1,C1A1
问题2: 和 相似吗?为什么?
思考
问题提出
问题辨析
深入探究
新知探究
ABC
A1B1C1
A1B1C1
ABC
利用位似放缩图形
课堂实施
新知探究
概念学习
概念应用
课堂小结
作业布置
新知引入
问题提出
问题辨析
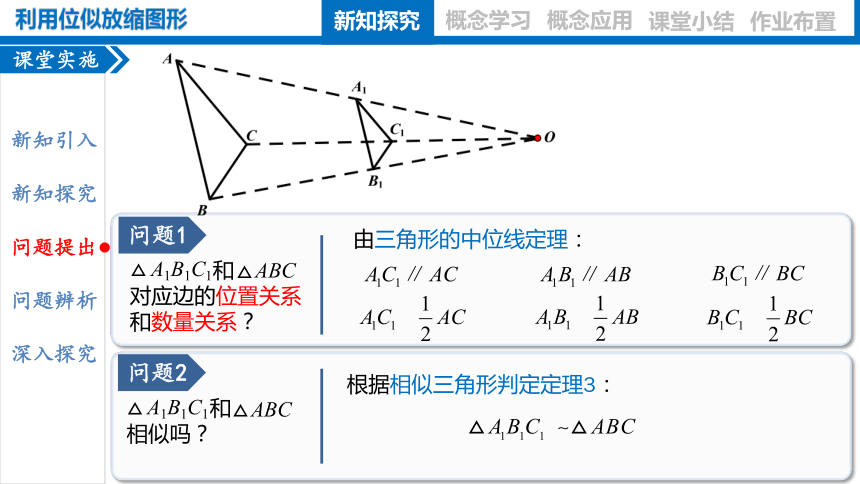
问题1
由三角形的中位线定理:
问题2
根据相似三角形判定定理3:
深入探究
新知探究
和 对应边的位置关系和数量关系?
A1B1C1
ABC
和 相似吗?
ABC
A1B1C1
利用位似放缩图形
问题3: 和 相似吗?
课堂实施
新知引入
问题提出
问题辨析
新知探究
概念学习
概念应用
课堂小结
作业布置
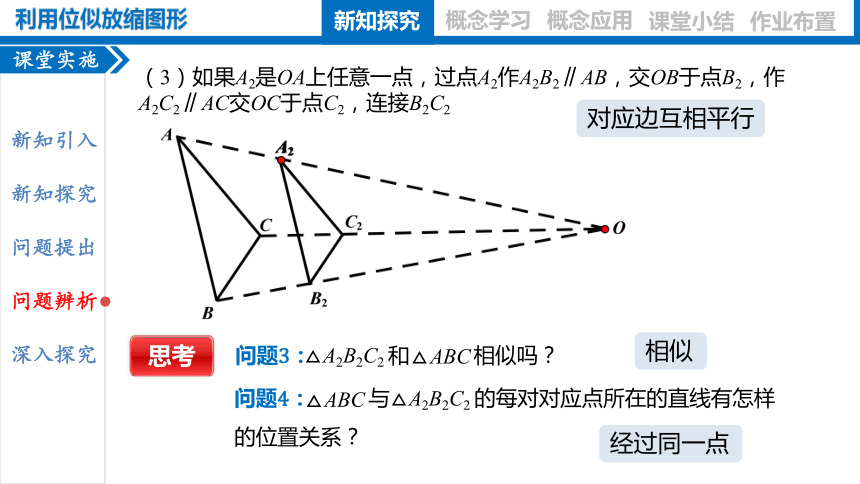
(3)如果A2是OA上任意一点,过点A2作A2B2∥AB,交OB于点B2,作A2C2∥AC交OC于点C2,连接B2C2
深入探究
问题4: 与 的每对对应点所在的直线有怎样的位置关系?
思考
新知探究
相似
经过同一点
对应边互相平行
ABC
A2B2C2
A2B2C2
ABC
利用位似放缩图形
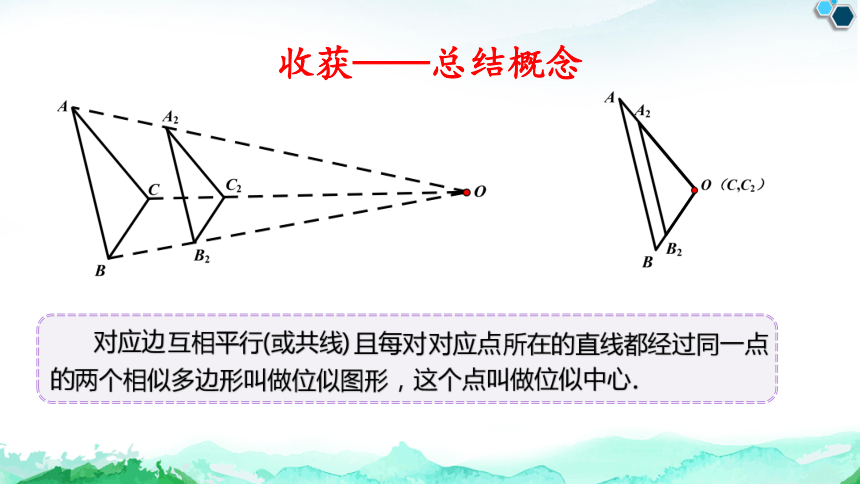
且每对 所在的直线都
的 叫做 ,这个点叫做 .
对应边
互相平行(或共线)
对应点
经过同一点
两个相似多边形
位似图形
位似中心
收获——总结概念
①位似图形上任意一对对应点到位似中心的距离之比等于相似比.
图中有哪些线段的比等于 与 的相似比?
课堂实施
新知探究
概念学习
概念应用
课堂小结
作业布置
位似中心
图形放缩
总结概念
探究性质
我学我会
概括方法
性质:
A2B2C2
ABC
位似比
利用位似放缩图形
新知探究
概念学习
概念应用
课堂小结
作业布置
位似中心
图形放缩
总结概念
探究性质
我学我会
概括方法
课堂实施
利用位似放缩图形
课堂实施
新知探究
概念学习
概念应用
课堂小结
作业布置
位似中心
图形放缩
总结概念
探究性质
我学我会
概括方法
①位似图形上任意一对对应点到位似中心的距离之比等于相似比.
性质:
②位似图形是特殊的相似图形.
利用位似放缩图形
新知探究
概念学习
概念应用
课堂小结
作业布置
位似中心
图形放缩
我学我会
总结概念
探究性质
概括方法
判断下列图形是不是位似图形,如果是位似图形,请指出位似中心;如果不是,请说明理由.
×
旋转
①两个相似多边形;
③对应点所在直线经过同一点.
②对应边互相平行或共线;
判定依据
√
×
课堂实施
利用位似放缩图形
图形的位似中心有哪几种情况?
外部
内部
公共顶点
边
思考
众人拾柴火焰高———小组合作
如图,已知 与点O,以点O为位似中心,画出 ,
使它与 是位似图形,并且相似比为3:2.
位似图形上任意一对对应点到位似中心的距离之比等于相似比.
新知探究
概念学习
概念应用
课堂小结
作业布置
我思我想
我学我做
我知我懂
实战
画法一:
画法二:
A字形
X形
图形的位似
课堂实施
(3) 对应点:根据相似比在射线上确定所画图形的顶点;
课堂实施
新知探究
概念学习
概念应用
课堂小结
我思我想
我知我懂
作业布置
我学我做
(4) 线:顺次连接各点.
位似图形的画法:
(2) 射线:以位似中心或多边形的各顶点为端点作射线;
选
作
定
连
(1) 点:确定位似中心O;
利用位似放缩图形
回扣目标
未来之星 (100分以上) 学习之星 (80分到100分) 进步之星
(80分以下)
你不仅能够运用知识解决问题,而且具备一个良好数学家的学习品质和思维能力, 你必是未来之星。 你不仅掌握了基本知识,还能够进行简单的应用,相信你一定可以超越自己,成为更加优秀的学习之星。
你基本能掌握本节课的知识,如果能够注重在具体问题中的灵魂应用的话,成功就会属于你。
位似图形相似图形对应边互相平行(或共线)对应点所在直线都经过同一点(位似中心)核心素养知识方法定义判定:位似图形一定是相似图形,相似图形不一定是位似图形。性质:画法:同A异X抽象类比从特殊到一般直观想象分类讨论
新知探究
概念学习
概念应用
课堂小结
作业布置
课本P125知识技能1、2
必做题
选做题
图形的位似
吾听吾忘,吾见吾记,吾做吾悟!
------《中庸》
课本P125数学理解、联系拓广
谢谢各位评委老师!
9.9 利用位似放缩图形(第一课时)
鲁教版8年级下册 第9章 图形的相似
学习目标
1、理解图形的位似概念,掌握图形位似的性质。
2、会利用作位似图形的方法把一个图形进行放大或缩小。
3、经历位似图形性质的探索过程,发展学生的探究、交流能力,培养学生数学结合思想。
理解定义
应用定义
掌握方法
课堂实施
新知探究
概念学习
概念应用
课堂小结
作业布置
手机屏幕
放大镜
大屏幕
新知引入
问题提出
问题辨析
深入探究
新知探究
利用位似放缩图形
从生活实例中抽象出数学模型
问题1: 和 的对应边有怎样的位置关系 和数量关系?
新知引入
课堂实施
新知探究
概念学习
概念应用
课堂小结
作业布置
(1)如图,连接 AO,BO,CO
(2)分别取 AO,BO,CO 的中点 A1,B1,C1,连接 A1B1,B1C1,C1A1
问题2: 和 相似吗?为什么?
思考
问题提出
问题辨析
深入探究
新知探究
ABC
A1B1C1
A1B1C1
ABC
利用位似放缩图形
课堂实施
新知探究
概念学习
概念应用
课堂小结
作业布置
新知引入
问题提出
问题辨析
问题1
由三角形的中位线定理:
问题2
根据相似三角形判定定理3:
深入探究
新知探究
和 对应边的位置关系和数量关系?
A1B1C1
ABC
和 相似吗?
ABC
A1B1C1
利用位似放缩图形
问题3: 和 相似吗?
课堂实施
新知引入
问题提出
问题辨析
新知探究
概念学习
概念应用
课堂小结
作业布置
(3)如果A2是OA上任意一点,过点A2作A2B2∥AB,交OB于点B2,作A2C2∥AC交OC于点C2,连接B2C2
深入探究
问题4: 与 的每对对应点所在的直线有怎样的位置关系?
思考
新知探究
相似
经过同一点
对应边互相平行
ABC
A2B2C2
A2B2C2
ABC
利用位似放缩图形
且每对 所在的直线都
的 叫做 ,这个点叫做 .
对应边
互相平行(或共线)
对应点
经过同一点
两个相似多边形
位似图形
位似中心
收获——总结概念
①位似图形上任意一对对应点到位似中心的距离之比等于相似比.
图中有哪些线段的比等于 与 的相似比?
课堂实施
新知探究
概念学习
概念应用
课堂小结
作业布置
位似中心
图形放缩
总结概念
探究性质
我学我会
概括方法
性质:
A2B2C2
ABC
位似比
利用位似放缩图形
新知探究
概念学习
概念应用
课堂小结
作业布置
位似中心
图形放缩
总结概念
探究性质
我学我会
概括方法
课堂实施
利用位似放缩图形
课堂实施
新知探究
概念学习
概念应用
课堂小结
作业布置
位似中心
图形放缩
总结概念
探究性质
我学我会
概括方法
①位似图形上任意一对对应点到位似中心的距离之比等于相似比.
性质:
②位似图形是特殊的相似图形.
利用位似放缩图形
新知探究
概念学习
概念应用
课堂小结
作业布置
位似中心
图形放缩
我学我会
总结概念
探究性质
概括方法
判断下列图形是不是位似图形,如果是位似图形,请指出位似中心;如果不是,请说明理由.
×
旋转
①两个相似多边形;
③对应点所在直线经过同一点.
②对应边互相平行或共线;
判定依据
√
×
课堂实施
利用位似放缩图形
图形的位似中心有哪几种情况?
外部
内部
公共顶点
边
思考
众人拾柴火焰高———小组合作
如图,已知 与点O,以点O为位似中心,画出 ,
使它与 是位似图形,并且相似比为3:2.
位似图形上任意一对对应点到位似中心的距离之比等于相似比.
新知探究
概念学习
概念应用
课堂小结
作业布置
我思我想
我学我做
我知我懂
实战
画法一:
画法二:
A字形
X形
图形的位似
课堂实施
(3) 对应点:根据相似比在射线上确定所画图形的顶点;
课堂实施
新知探究
概念学习
概念应用
课堂小结
我思我想
我知我懂
作业布置
我学我做
(4) 线:顺次连接各点.
位似图形的画法:
(2) 射线:以位似中心或多边形的各顶点为端点作射线;
选
作
定
连
(1) 点:确定位似中心O;
利用位似放缩图形
回扣目标
未来之星 (100分以上) 学习之星 (80分到100分) 进步之星
(80分以下)
你不仅能够运用知识解决问题,而且具备一个良好数学家的学习品质和思维能力, 你必是未来之星。 你不仅掌握了基本知识,还能够进行简单的应用,相信你一定可以超越自己,成为更加优秀的学习之星。
你基本能掌握本节课的知识,如果能够注重在具体问题中的灵魂应用的话,成功就会属于你。
位似图形相似图形对应边互相平行(或共线)对应点所在直线都经过同一点(位似中心)核心素养知识方法定义判定:位似图形一定是相似图形,相似图形不一定是位似图形。性质:画法:同A异X抽象类比从特殊到一般直观想象分类讨论
新知探究
概念学习
概念应用
课堂小结
作业布置
课本P125知识技能1、2
必做题
选做题
图形的位似
吾听吾忘,吾见吾记,吾做吾悟!
------《中庸》
课本P125数学理解、联系拓广
谢谢各位评委老师!
