江苏省扬州中学2024-2025学年高三(上)学科水平测试物理试卷(12月)(含答案)
文档属性
| 名称 | 江苏省扬州中学2024-2025学年高三(上)学科水平测试物理试卷(12月)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-06 15:09:14 | ||
图片预览



文档简介
江苏省扬州中学2024-2025学年高三(上)学科水平测试物理试卷(12月)
一、单选题:本大题共11小题,共44分。
1.科学家们创造出了许多物理思维方法,如理想实验法、控制变量法、极限思想法、模型法、类比法和比值定义法等等。以下关于所用物理学研究方法的叙述正确的是( )
A. 根据速度定义式,当非常小时,就可以用表示物体在某时刻的瞬时速度,应用了微元法
B. 在探究两个互成角度的力的合成规律时,采用了控制变量的方法
C. 在不需要考虑物体本身的大小和形状时,用质点代替物体的方法,采用了等效替代的思想
D. 加速度的定义采用的是比值定义法
2.某同学自己动手为手机贴钢化膜,贴完后发现屏幕中央有不规则的环形条纹,通过查询相关资料得知,这是由于钢化膜与手机屏幕之间存在空气薄膜造成的,出现环形条纹现象是光的( )
A. 衍射现象 B. 干涉现象 C. 偏振现象 D. 全反射现象
3.如图是半径为的半球形碗,一质量为的小物块从碗口点以大小不变的速度沿着碗滑到碗底中心点。则在该过程中( )
A. 小物块的动量不变 B. 小物块受到的合外力不变
C. 小物块受到的摩擦力不断减小 D. 小物块重力的功率先增大后减小
4.“打水漂”是一种常见的娱乐活动,以一定的高度水平扔出的瓦片,会反复在水面上弹跳前进,假设瓦片和水面相撞后,在水平和竖直方向速度大小均减小,以下四幅图有可能是瓦片轨迹的是( )
A. B.
C. D.
5.北京时间年月出现了“火星合日”现象,即当火星和地球分别位于太阳两侧与太阳共线干扰无线电时,影响通信的天文现象,因此中国首辆火星车“祝融号”在火星赤道表面附近做匀速圆周运动发生短暂“失联”。已知地球与火星绕太阳做匀速圆周运动的方向相同,火星和地球的公转轨道半径之比约为,引力常量为,则下列说法正确的是( )
A. 火星与地球绕太阳运动的线速度之比约为
B. 出现“火星合日”现象时,火星和地球的相对速度最大
C. 火星与地球表面的重力加速度大小之比约为
D. 下一次“火星合日”将出现在年月之前
6.如图,由、两种单色光组成的复色光,沿半球形水雾的半径方向入射,折射后分成两种单色光、。其中,光与界面的夹角为,光的折射率为,光与法线的夹角为,光在空气中的传播速度为,水雾半球的半径为。下列说法中正确的是( )
A. 光在半球水雾中的传播时间为
B. 光在半球水雾中的传播时间为
C. 单色光的频率比单色光的频率小
D. 利用、单色光做双缝干涉实验,在相同实验条件下,光比光的条纹间距大
7.周村古商城有一件古代青铜“鱼洗”复制品,在其中加入适量清水后,用手有节奏地摩擦“鱼洗”的双耳,会发出嗡嗡声,并能使盆内水花四溅,如图甲所示。图乙为某时刻相向传播的两列同频率水波的波形图,、、、四个位置中最有可能“喷出水花”的位置是( )
A. 位置 B. 位置 C. 位置 D. 位置
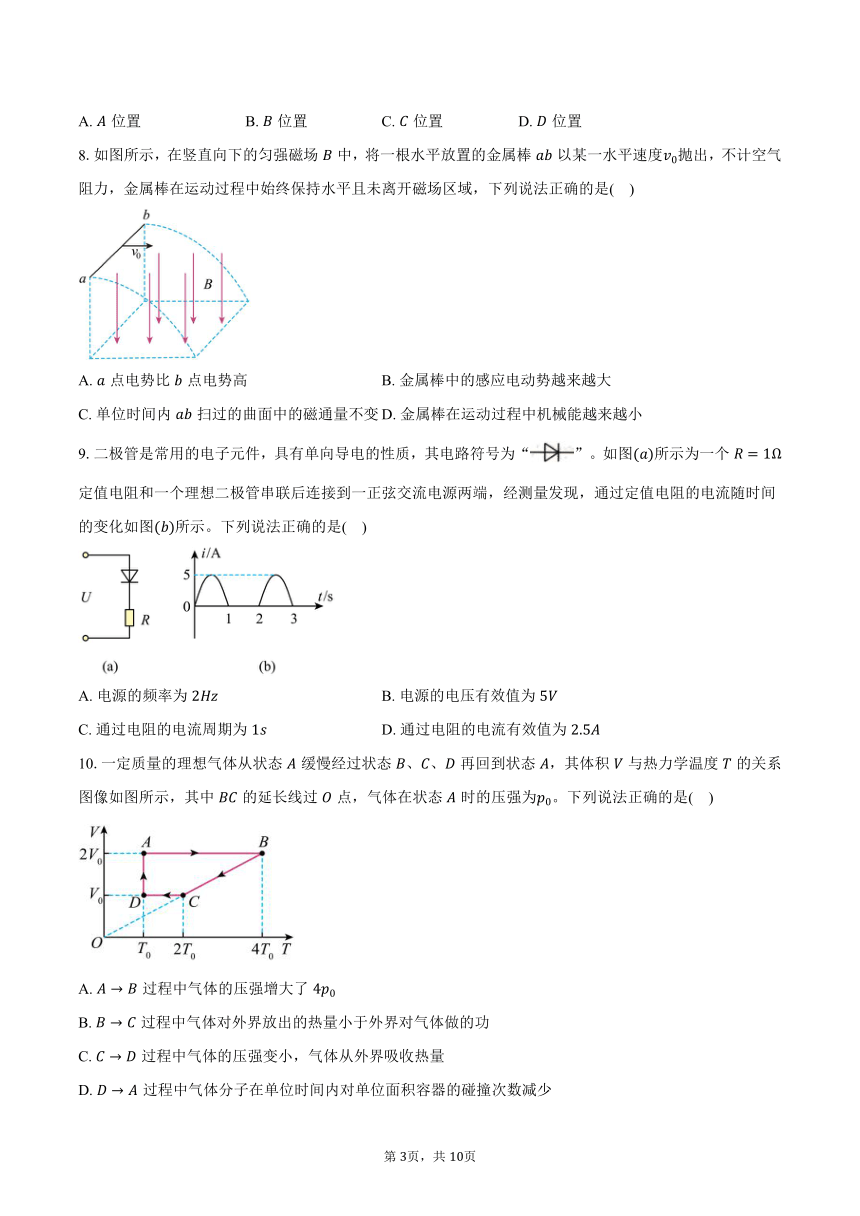
8.如图所示,在竖直向下的匀强磁场中,将一根水平放置的金属棒以某一水平速度抛出,不计空气阻力,金属棒在运动过程中始终保持水平且未离开磁场区域,下列说法正确的是( )
A. 点电势比点电势高 B. 金属棒中的感应电动势越来越大
C. 单位时间内扫过的曲面中的磁通量不变 D. 金属棒在运动过程中机械能越来越小
9.二极管是常用的电子元件,具有单向导电的性质,其电路符号为“”。如图所示为一个定值电阻和一个理想二极管串联后连接到一正弦交流电源两端,经测量发现,通过定值电阻的电流随时间的变化如图所示。下列说法正确的是( )
A. 电源的频率为 B. 电源的电压有效值为
C. 通过电阻的电流周期为 D. 通过电阻的电流有效值为
10.一定质量的理想气体从状态缓慢经过状态、、再回到状态,其体积与热力学温度的关系图像如图所示,其中的延长线过点,气体在状态时的压强为。下列说法正确的是( )
A. 过程中气体的压强增大了
B. 过程中气体对外界放出的热量小于外界对气体做的功
C. 过程中气体的压强变小,气体从外界吸收热量
D. 过程中气体分子在单位时间内对单位面积容器的碰撞次数减少
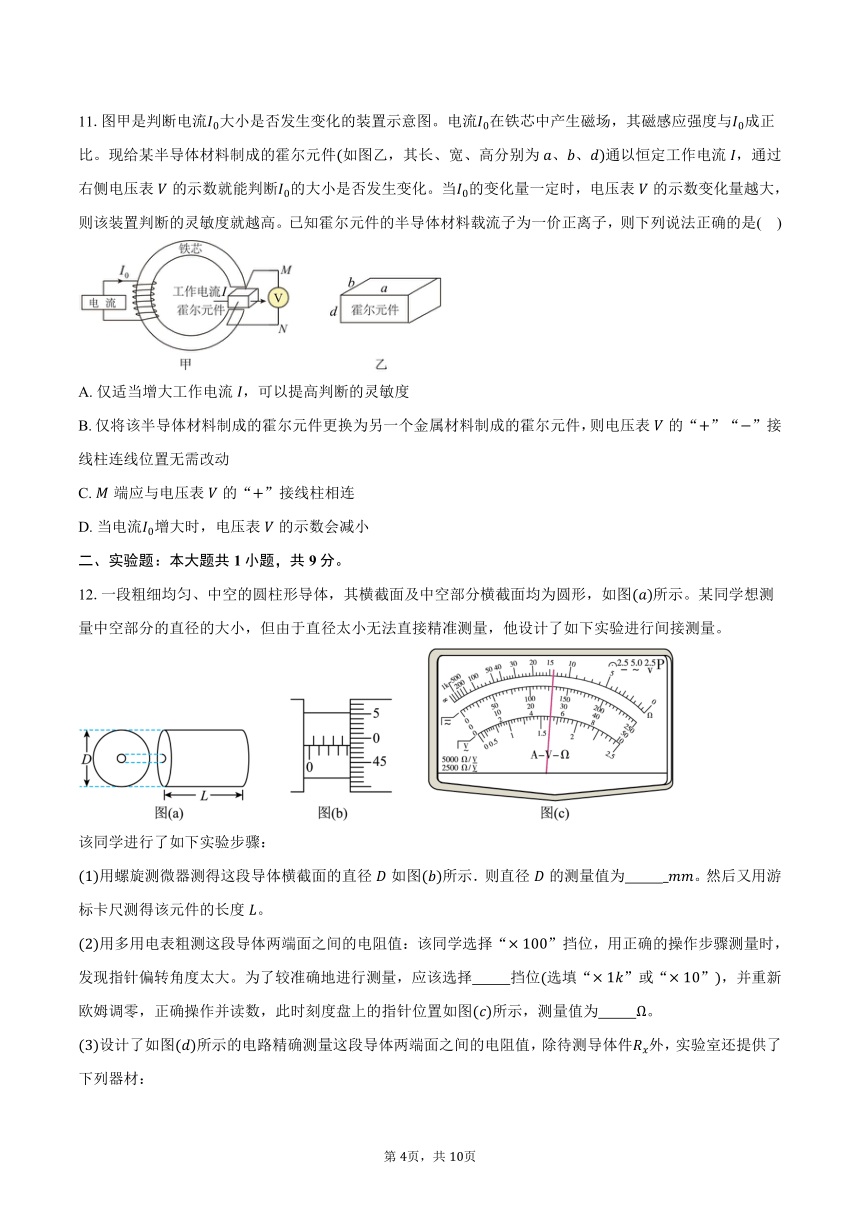
11.图甲是判断电流大小是否发生变化的装置示意图。电流在铁芯中产生磁场,其磁感应强度与成正比。现给某半导体材料制成的霍尔元件如图乙,其长、宽、高分别为、、通以恒定工作电流,通过右侧电压表的示数就能判断的大小是否发生变化。当的变化量一定时,电压表的示数变化量越大,则该装置判断的灵敏度就越高。已知霍尔元件的半导体材料载流子为一价正离子,则下列说法正确的是( )
A. 仅适当增大工作电流,可以提高判断的灵敏度
B. 仅将该半导体材料制成的霍尔元件更换为另一个金属材料制成的霍尔元件,则电压表的“”“”接线柱连线位置无需改动
C. 端应与电压表的“”接线柱相连
D. 当电流增大时,电压表的示数会减小
二、实验题:本大题共1小题,共9分。
12.一段粗细均匀、中空的圆柱形导体,其横截面及中空部分横截面均为圆形,如图所示。某同学想测量中空部分的直径的大小,但由于直径太小无法直接精准测量,他设计了如下实验进行间接测量。
该同学进行了如下实验步骤:
用螺旋测微器测得这段导体横截面的直径如图所示.则直径的测量值为 。然后又用游标卡尺测得该元件的长度。
用多用电表粗测这段导体两端面之间的电阻值:该同学选择“”挡位,用正确的操作步骤测量时,发现指针偏转角度太大。为了较准确地进行测量,应该选择 挡位选填“”或“”,并重新欧姆调零,正确操作并读数,此时刻度盘上的指针位置如图所示,测量值为 。
设计了如图所示的电路精确测量这段导体两端面之间的电阻值,除待测导体件外,实验室还提供了下列器材:
A.电流表量程为,内阻
B.电流表量程为内阻未知
C.滑动变阻器
D.定值电阻
E.定值电阻
F.电源电动势,内阻可以忽略
G.开关、导线若干
根据以上器材和粗测导体电阻值的情况可知,电路中定值电阻应选择 填器材前面的字母代号;为了减小误差,改变滑动变阻器滑动触头的位置,多测几组、的值,作出关系图像如图所示。若读出图线上某点对应的、的坐标值分别为和,则可知这段导体两端面间电阻的测量值 用图像中数据和题设给出的物理量符号表示
该同学查出这段导体材料的电阻率,则中空部分的直径大小测量值为 用图像中数据和题设给出的物理量符号表示。
三、计算题:本大题共4小题,共40分。
13.在我国南海上有一浮桶式波浪发电灯塔,其原理如图甲所示。浮桶内的磁体通过支柱固定在暗礁上,浮桶内置圆形线圈随波浪相对磁体沿竖直方向运动,上下运动的速度,且始终处于辐射磁场中,该线圈与阻值的灯泡相连;浮桶下部由内、外两密封圆筒构成俯视图乙中阴影部分,其内部为产生磁场的磁体;线圈匝数匝,线圈所在处磁场的磁感应强度大小,圆形线圈的直径,电阻。计算时取。
求线圈中产生感应电动势的最大值;
求灯泡工作时消耗的电功率。
14.年,伽利略用自制的望远镜发现了木星的四颗主要卫星。根据他的观察,其中一颗卫星做振幅为、周期为的简谐运动,他推测该卫星振动是卫星做圆周运动在某方向上的投影。如图所示是卫星运动的示意图,在平面内,质量为的卫星绕坐标原点做匀速圆周运动。若认为木星位于坐标原点,求:
卫星做圆周运动的向心力大小;
物体做简谐运动时,回复力应满足。试证明:卫星绕木星做匀速圆周运动在轴上的投影是简谐运动。
15.如图所示,质量为的木块、,并排放在光滑水平面上,木块上固定一竖直轻杆,轻杆上端的点系一长为的细线,细线另一端系一质量为的球。现将球拉起使细线水平伸直,并由静止释放球。重力加速度为求:
球从水平位置到最低点过程中,木块移动的距离;
、两木块分离时,、、三者的速度大小;
小球第一次到达左侧的最大高度。
16.如图所示,坐标系平面在纸面内,在的区域存在垂直纸面向外的匀强磁场,的区域Ⅰ和的区域Ⅱ的磁感应强度大小分别为和大量质量为、电荷量为的带正电的粒子从原点在坐标平面内向与正方向成角射入,粒子的速度大小相等,方向随角度均匀分布沿轴正方向射入的粒子在点垂直两磁场的边界射入区域Ⅱ不计粒子的重力和粒子间的相互作用.
求粒子从原点射入磁场时的速度大小;
若在两磁场分界处有一垂直于平面的足够大竖直挡板,求打到挡板上的粒子数占总粒子数的百分比;
若粒子在区域Ⅱ中受到与速度大小成正比、方向相反的阻力,比例系数为,观察发现沿轴正方向射入的粒子,射入区域Ⅱ后粒子轨迹呈螺旋状并与两磁场的边界相切于点未画出,求该粒子由点运动到点的时间及该粒子在区域Ⅱ中运动轨迹的长度.
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】解:线圈在磁场中切割磁感线,产生电动势最大值为:,
其中:,
联立得:;
电动势的有效值为:
根据闭合电路欧姆定律有:
则灯泡的功率为:
联立解得:
答:线圈中产生感应电动势的最大值为;
灯泡工作时消耗的电功率为。
14.【答案】卫星做圆周运动的向心力大小为
如图
取向右为正方向,则
则卫星绕木星做匀速圆周运动在轴上的投影是简谐运动。
15.【答案】球从水平位置到最低点过程中,、、组成的系统水平方向动量守恒,且、速度相同,则有
即
又因为
联立可得
当球第一次摆到最低点时,、两木块分离,此刻、速度相等,设、速度大小为、球速度大小为,、、系统水平方向动量守恒有
A、、系统机械能守恒有
联立可得
即、两木块分离时,、、三者的速度大小均为。
球摆到竖直轻杆左侧最大高度时,、共速设为,最大高度为,、系统水平方向上动量守恒有
A、系统机械能守恒有
得此时球与点的竖直距离。
16.【答案】解:洛伦兹力提供向心力
又
解得;
由,当初速度方向沿轴正向时,轨迹与磁场边界相切,此时粒子刚好打到挡板上,
范围内的粒子都能打到挡板,所以打到挡板上的粒子数占总粒子数的百分比
;
该粒子在区域Ⅱ中的运动轨迹如图所示:
洛伦兹力提供向心力
可得
即角速度为一定值,又可知粒子与边界相切时转过的弧度为
时间
解得
粒子在区域Ⅱ中做螺旋线运动,由于阻力最后停下来
在切线方向上,牛顿第二定律
有
求和得
解得
第1页,共1页
一、单选题:本大题共11小题,共44分。
1.科学家们创造出了许多物理思维方法,如理想实验法、控制变量法、极限思想法、模型法、类比法和比值定义法等等。以下关于所用物理学研究方法的叙述正确的是( )
A. 根据速度定义式,当非常小时,就可以用表示物体在某时刻的瞬时速度,应用了微元法
B. 在探究两个互成角度的力的合成规律时,采用了控制变量的方法
C. 在不需要考虑物体本身的大小和形状时,用质点代替物体的方法,采用了等效替代的思想
D. 加速度的定义采用的是比值定义法
2.某同学自己动手为手机贴钢化膜,贴完后发现屏幕中央有不规则的环形条纹,通过查询相关资料得知,这是由于钢化膜与手机屏幕之间存在空气薄膜造成的,出现环形条纹现象是光的( )
A. 衍射现象 B. 干涉现象 C. 偏振现象 D. 全反射现象
3.如图是半径为的半球形碗,一质量为的小物块从碗口点以大小不变的速度沿着碗滑到碗底中心点。则在该过程中( )
A. 小物块的动量不变 B. 小物块受到的合外力不变
C. 小物块受到的摩擦力不断减小 D. 小物块重力的功率先增大后减小
4.“打水漂”是一种常见的娱乐活动,以一定的高度水平扔出的瓦片,会反复在水面上弹跳前进,假设瓦片和水面相撞后,在水平和竖直方向速度大小均减小,以下四幅图有可能是瓦片轨迹的是( )
A. B.
C. D.
5.北京时间年月出现了“火星合日”现象,即当火星和地球分别位于太阳两侧与太阳共线干扰无线电时,影响通信的天文现象,因此中国首辆火星车“祝融号”在火星赤道表面附近做匀速圆周运动发生短暂“失联”。已知地球与火星绕太阳做匀速圆周运动的方向相同,火星和地球的公转轨道半径之比约为,引力常量为,则下列说法正确的是( )
A. 火星与地球绕太阳运动的线速度之比约为
B. 出现“火星合日”现象时,火星和地球的相对速度最大
C. 火星与地球表面的重力加速度大小之比约为
D. 下一次“火星合日”将出现在年月之前
6.如图,由、两种单色光组成的复色光,沿半球形水雾的半径方向入射,折射后分成两种单色光、。其中,光与界面的夹角为,光的折射率为,光与法线的夹角为,光在空气中的传播速度为,水雾半球的半径为。下列说法中正确的是( )
A. 光在半球水雾中的传播时间为
B. 光在半球水雾中的传播时间为
C. 单色光的频率比单色光的频率小
D. 利用、单色光做双缝干涉实验,在相同实验条件下,光比光的条纹间距大
7.周村古商城有一件古代青铜“鱼洗”复制品,在其中加入适量清水后,用手有节奏地摩擦“鱼洗”的双耳,会发出嗡嗡声,并能使盆内水花四溅,如图甲所示。图乙为某时刻相向传播的两列同频率水波的波形图,、、、四个位置中最有可能“喷出水花”的位置是( )
A. 位置 B. 位置 C. 位置 D. 位置
8.如图所示,在竖直向下的匀强磁场中,将一根水平放置的金属棒以某一水平速度抛出,不计空气阻力,金属棒在运动过程中始终保持水平且未离开磁场区域,下列说法正确的是( )
A. 点电势比点电势高 B. 金属棒中的感应电动势越来越大
C. 单位时间内扫过的曲面中的磁通量不变 D. 金属棒在运动过程中机械能越来越小
9.二极管是常用的电子元件,具有单向导电的性质,其电路符号为“”。如图所示为一个定值电阻和一个理想二极管串联后连接到一正弦交流电源两端,经测量发现,通过定值电阻的电流随时间的变化如图所示。下列说法正确的是( )
A. 电源的频率为 B. 电源的电压有效值为
C. 通过电阻的电流周期为 D. 通过电阻的电流有效值为
10.一定质量的理想气体从状态缓慢经过状态、、再回到状态,其体积与热力学温度的关系图像如图所示,其中的延长线过点,气体在状态时的压强为。下列说法正确的是( )
A. 过程中气体的压强增大了
B. 过程中气体对外界放出的热量小于外界对气体做的功
C. 过程中气体的压强变小,气体从外界吸收热量
D. 过程中气体分子在单位时间内对单位面积容器的碰撞次数减少
11.图甲是判断电流大小是否发生变化的装置示意图。电流在铁芯中产生磁场,其磁感应强度与成正比。现给某半导体材料制成的霍尔元件如图乙,其长、宽、高分别为、、通以恒定工作电流,通过右侧电压表的示数就能判断的大小是否发生变化。当的变化量一定时,电压表的示数变化量越大,则该装置判断的灵敏度就越高。已知霍尔元件的半导体材料载流子为一价正离子,则下列说法正确的是( )
A. 仅适当增大工作电流,可以提高判断的灵敏度
B. 仅将该半导体材料制成的霍尔元件更换为另一个金属材料制成的霍尔元件,则电压表的“”“”接线柱连线位置无需改动
C. 端应与电压表的“”接线柱相连
D. 当电流增大时,电压表的示数会减小
二、实验题:本大题共1小题,共9分。
12.一段粗细均匀、中空的圆柱形导体,其横截面及中空部分横截面均为圆形,如图所示。某同学想测量中空部分的直径的大小,但由于直径太小无法直接精准测量,他设计了如下实验进行间接测量。
该同学进行了如下实验步骤:
用螺旋测微器测得这段导体横截面的直径如图所示.则直径的测量值为 。然后又用游标卡尺测得该元件的长度。
用多用电表粗测这段导体两端面之间的电阻值:该同学选择“”挡位,用正确的操作步骤测量时,发现指针偏转角度太大。为了较准确地进行测量,应该选择 挡位选填“”或“”,并重新欧姆调零,正确操作并读数,此时刻度盘上的指针位置如图所示,测量值为 。
设计了如图所示的电路精确测量这段导体两端面之间的电阻值,除待测导体件外,实验室还提供了下列器材:
A.电流表量程为,内阻
B.电流表量程为内阻未知
C.滑动变阻器
D.定值电阻
E.定值电阻
F.电源电动势,内阻可以忽略
G.开关、导线若干
根据以上器材和粗测导体电阻值的情况可知,电路中定值电阻应选择 填器材前面的字母代号;为了减小误差,改变滑动变阻器滑动触头的位置,多测几组、的值,作出关系图像如图所示。若读出图线上某点对应的、的坐标值分别为和,则可知这段导体两端面间电阻的测量值 用图像中数据和题设给出的物理量符号表示
该同学查出这段导体材料的电阻率,则中空部分的直径大小测量值为 用图像中数据和题设给出的物理量符号表示。
三、计算题:本大题共4小题,共40分。
13.在我国南海上有一浮桶式波浪发电灯塔,其原理如图甲所示。浮桶内的磁体通过支柱固定在暗礁上,浮桶内置圆形线圈随波浪相对磁体沿竖直方向运动,上下运动的速度,且始终处于辐射磁场中,该线圈与阻值的灯泡相连;浮桶下部由内、外两密封圆筒构成俯视图乙中阴影部分,其内部为产生磁场的磁体;线圈匝数匝,线圈所在处磁场的磁感应强度大小,圆形线圈的直径,电阻。计算时取。
求线圈中产生感应电动势的最大值;
求灯泡工作时消耗的电功率。
14.年,伽利略用自制的望远镜发现了木星的四颗主要卫星。根据他的观察,其中一颗卫星做振幅为、周期为的简谐运动,他推测该卫星振动是卫星做圆周运动在某方向上的投影。如图所示是卫星运动的示意图,在平面内,质量为的卫星绕坐标原点做匀速圆周运动。若认为木星位于坐标原点,求:
卫星做圆周运动的向心力大小;
物体做简谐运动时,回复力应满足。试证明:卫星绕木星做匀速圆周运动在轴上的投影是简谐运动。
15.如图所示,质量为的木块、,并排放在光滑水平面上,木块上固定一竖直轻杆,轻杆上端的点系一长为的细线,细线另一端系一质量为的球。现将球拉起使细线水平伸直,并由静止释放球。重力加速度为求:
球从水平位置到最低点过程中,木块移动的距离;
、两木块分离时,、、三者的速度大小;
小球第一次到达左侧的最大高度。
16.如图所示,坐标系平面在纸面内,在的区域存在垂直纸面向外的匀强磁场,的区域Ⅰ和的区域Ⅱ的磁感应强度大小分别为和大量质量为、电荷量为的带正电的粒子从原点在坐标平面内向与正方向成角射入,粒子的速度大小相等,方向随角度均匀分布沿轴正方向射入的粒子在点垂直两磁场的边界射入区域Ⅱ不计粒子的重力和粒子间的相互作用.
求粒子从原点射入磁场时的速度大小;
若在两磁场分界处有一垂直于平面的足够大竖直挡板,求打到挡板上的粒子数占总粒子数的百分比;
若粒子在区域Ⅱ中受到与速度大小成正比、方向相反的阻力,比例系数为,观察发现沿轴正方向射入的粒子,射入区域Ⅱ后粒子轨迹呈螺旋状并与两磁场的边界相切于点未画出,求该粒子由点运动到点的时间及该粒子在区域Ⅱ中运动轨迹的长度.
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】解:线圈在磁场中切割磁感线,产生电动势最大值为:,
其中:,
联立得:;
电动势的有效值为:
根据闭合电路欧姆定律有:
则灯泡的功率为:
联立解得:
答:线圈中产生感应电动势的最大值为;
灯泡工作时消耗的电功率为。
14.【答案】卫星做圆周运动的向心力大小为
如图
取向右为正方向,则
则卫星绕木星做匀速圆周运动在轴上的投影是简谐运动。
15.【答案】球从水平位置到最低点过程中,、、组成的系统水平方向动量守恒,且、速度相同,则有
即
又因为
联立可得
当球第一次摆到最低点时,、两木块分离,此刻、速度相等,设、速度大小为、球速度大小为,、、系统水平方向动量守恒有
A、、系统机械能守恒有
联立可得
即、两木块分离时,、、三者的速度大小均为。
球摆到竖直轻杆左侧最大高度时,、共速设为,最大高度为,、系统水平方向上动量守恒有
A、系统机械能守恒有
得此时球与点的竖直距离。
16.【答案】解:洛伦兹力提供向心力
又
解得;
由,当初速度方向沿轴正向时,轨迹与磁场边界相切,此时粒子刚好打到挡板上,
范围内的粒子都能打到挡板,所以打到挡板上的粒子数占总粒子数的百分比
;
该粒子在区域Ⅱ中的运动轨迹如图所示:
洛伦兹力提供向心力
可得
即角速度为一定值,又可知粒子与边界相切时转过的弧度为
时间
解得
粒子在区域Ⅱ中做螺旋线运动,由于阻力最后停下来
在切线方向上,牛顿第二定律
有
求和得
解得
第1页,共1页
同课章节目录
