27.2.1 点与圆的位置关系(共20张PPT)2024-2025学年华师大版数学九年级下册
文档属性
| 名称 | 27.2.1 点与圆的位置关系(共20张PPT)2024-2025学年华师大版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-07 11:36:57 | ||
图片预览



文档简介
(共19张PPT)
27.2.1 点与圆的位置关系
1.理解点与圆的三种位置关系,并能判断点与圆的位置关系;
2.探索不在同一条直线上的三个点确定一个圆的结论,会过不在同一条直线上的三个点作圆;
3.了解三角形外接圆的概念及外心的性质.
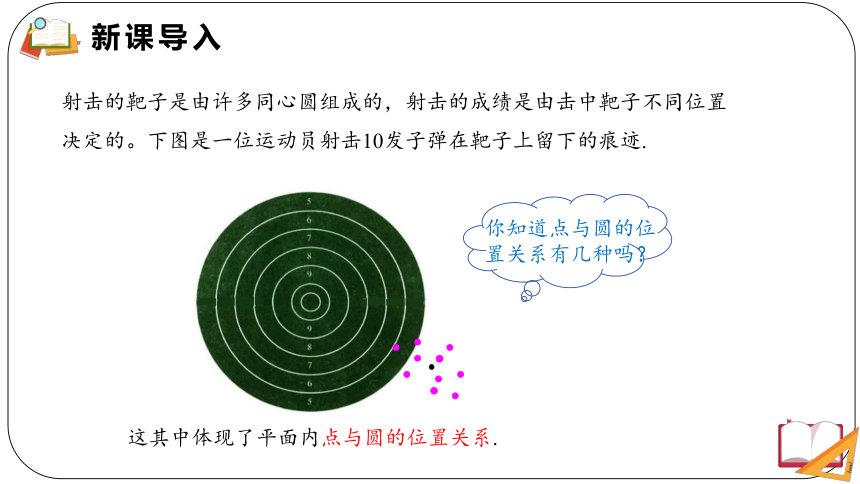
射击的靶子是由许多同心圆组成的,射击的成绩是由击中靶子不同位置决定的。下图是一位运动员射击10发子弹在靶子上留下的痕迹.
这其中体现了平面内点与圆的位置关系.
你知道点与圆的位置关系有几种吗?
问题1:观察图中点和圆的位置关系有哪几种?
O
.
B
.
.
.
.
.
C
.
A
.
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
点和圆的位置关系
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
P
d
P
r
d
P
r
d
<
r
r
=
>
r
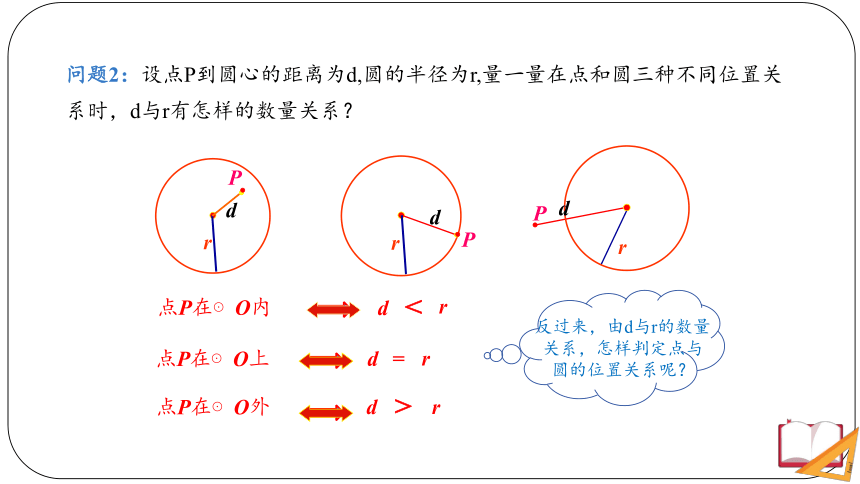
问题2:设点P到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
r
P
d
P
d
P
d
O
O
O
r
r
R
r
P
O
d
数形结合:
位置关系
数量关系
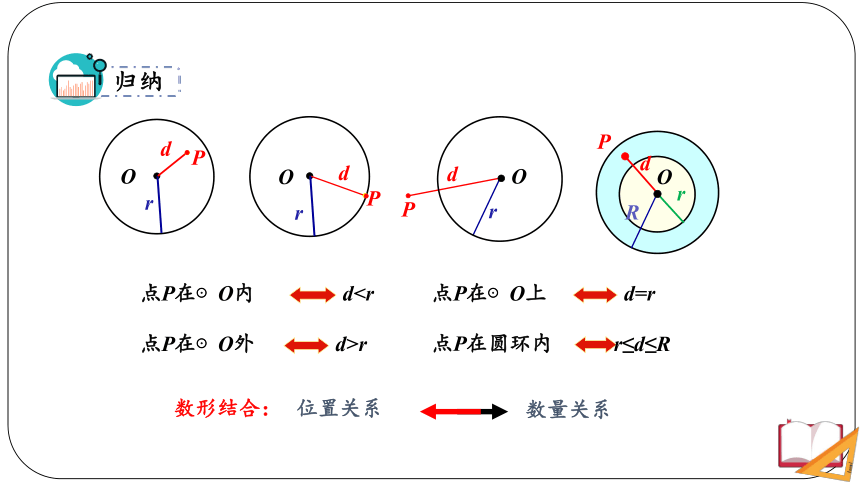
点P在⊙O内
d点P在⊙O上
d=r
点P在⊙O外
d>r
点P在圆环内
r≤d≤R
归纳
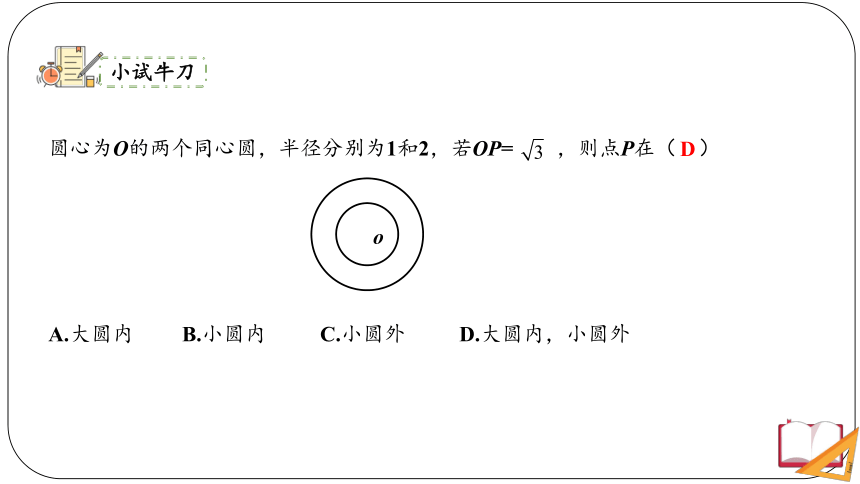
圆心为O的两个同心圆,半径分别为1和2,若OP= ,则点P在( )
A.大圆内 B.小圆内 C.小圆外 D.大圆内,小圆外
D
o
小试牛刀
·
·
·
·
·
以不与A点重合的任意一点为圆心,以这个点到A点的距离为半径画圆可作无数个圆.
A
问题1:经过已知点A作圆,这样的圆你能作出多少个?
过不在同一直线上的三点作圆
问题2:经过已知点A,B作圆,这样的圆你能作出多少个?圆心分布有什么特点?
A
B
·
·
·
·
经过平面内两个点可以作无数个圆,圆心都在线段AB的垂直平分线上.
问题3:经过不在同一条直线上的三个点确定一个圆,如何确定这个圆的圆心?
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
不在同一条直线上的三个点确定一个圆.
位置关系
数量关系
归纳
已知△ABC,用直尺与圆规作出过 A、B、C三点的圆.
A
B
C
O
三角形的外接圆及外心
试一试
1.三角形的外接圆:经过三角形三个顶点的圆叫做三角形的外接圆,这个三角形叫做圆的内接三角形.
2.三角形的外心:三角形的外接圆的圆心叫做这个三角形的外心.
作图:三角形三条边的垂直平分线的交点.
性质:三角形的外心到三角形三个顶点的距离相等.
注意:任意一个三角形都有且只有一个外接圆,而一个圆有无数个内接三角形.
概念生成
●O
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
A
B
C
A
B
C
C
A
B
┐
●O
●O
锐角三角形:内部
直角三角形:
斜边中点
钝角三角形:外部
拓展
1.若⊙O的半径为5,圆心O的坐标为(3,4),点P的坐标为(5,2),则点P与⊙O的位置关系是( )
A.点P在⊙O内
B.点P在⊙O上
C.点P在⊙O外
D.点P在⊙O上或在⊙O外
B
2.下列四个命题中,正确的有( )
①直径是弦;
②任意三点确定一个圆;
③三角形的外心到三角形各顶点的距离都相等;
④相等的圆心角所对的弧相等.
A.4个 B.3个 C.2个 D.1个
C
3.已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,则它的外接圆半径= .
5
4.若点O为△ABC的外心,∠BOC=50°,则∠BAC等于 .
25°或155°
5.随意画出四个点,其中任何三点都不在同一条直线上,是否一定可以画出一个圆经过这四点?请举例说明。
不一定.理由如下:先过不在同一直线上的三点作圆若第四点到圆心的距离等于半径,则第四点在这个圆上,此时这四个点共圆;
若第四点到圆心的距离不等于半径,则第四点不在这个圆上,此时这四个点不共圆。
点和圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d位置关系数量化
作圆
过一点可以作无数个圆
过两点可以作无数个圆
不在同一直线上的三个点可确定一个圆
一个三角形的
外接圆是唯一的
注意:过同一直线上的三个点不能作圆
点 P 在圆环内
r≤d≤R
R
r
P
O
d
27.2.1 点与圆的位置关系
1.理解点与圆的三种位置关系,并能判断点与圆的位置关系;
2.探索不在同一条直线上的三个点确定一个圆的结论,会过不在同一条直线上的三个点作圆;
3.了解三角形外接圆的概念及外心的性质.
射击的靶子是由许多同心圆组成的,射击的成绩是由击中靶子不同位置决定的。下图是一位运动员射击10发子弹在靶子上留下的痕迹.
这其中体现了平面内点与圆的位置关系.
你知道点与圆的位置关系有几种吗?
问题1:观察图中点和圆的位置关系有哪几种?
O
.
B
.
.
.
.
.
C
.
A
.
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
点和圆的位置关系
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
P
d
P
r
d
P
r
d
<
r
r
=
>
r
问题2:设点P到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
r
P
d
P
d
P
d
O
O
O
r
r
R
r
P
O
d
数形结合:
位置关系
数量关系
点P在⊙O内
d
d=r
点P在⊙O外
d>r
点P在圆环内
r≤d≤R
归纳
圆心为O的两个同心圆,半径分别为1和2,若OP= ,则点P在( )
A.大圆内 B.小圆内 C.小圆外 D.大圆内,小圆外
D
o
小试牛刀
·
·
·
·
·
以不与A点重合的任意一点为圆心,以这个点到A点的距离为半径画圆可作无数个圆.
A
问题1:经过已知点A作圆,这样的圆你能作出多少个?
过不在同一直线上的三点作圆
问题2:经过已知点A,B作圆,这样的圆你能作出多少个?圆心分布有什么特点?
A
B
·
·
·
·
经过平面内两个点可以作无数个圆,圆心都在线段AB的垂直平分线上.
问题3:经过不在同一条直线上的三个点确定一个圆,如何确定这个圆的圆心?
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
不在同一条直线上的三个点确定一个圆.
位置关系
数量关系
归纳
已知△ABC,用直尺与圆规作出过 A、B、C三点的圆.
A
B
C
O
三角形的外接圆及外心
试一试
1.三角形的外接圆:经过三角形三个顶点的圆叫做三角形的外接圆,这个三角形叫做圆的内接三角形.
2.三角形的外心:三角形的外接圆的圆心叫做这个三角形的外心.
作图:三角形三条边的垂直平分线的交点.
性质:三角形的外心到三角形三个顶点的距离相等.
注意:任意一个三角形都有且只有一个外接圆,而一个圆有无数个内接三角形.
概念生成
●O
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
A
B
C
A
B
C
C
A
B
┐
●O
●O
锐角三角形:内部
直角三角形:
斜边中点
钝角三角形:外部
拓展
1.若⊙O的半径为5,圆心O的坐标为(3,4),点P的坐标为(5,2),则点P与⊙O的位置关系是( )
A.点P在⊙O内
B.点P在⊙O上
C.点P在⊙O外
D.点P在⊙O上或在⊙O外
B
2.下列四个命题中,正确的有( )
①直径是弦;
②任意三点确定一个圆;
③三角形的外心到三角形各顶点的距离都相等;
④相等的圆心角所对的弧相等.
A.4个 B.3个 C.2个 D.1个
C
3.已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,则它的外接圆半径= .
5
4.若点O为△ABC的外心,∠BOC=50°,则∠BAC等于 .
25°或155°
5.随意画出四个点,其中任何三点都不在同一条直线上,是否一定可以画出一个圆经过这四点?请举例说明。
不一定.理由如下:先过不在同一直线上的三点作圆若第四点到圆心的距离等于半径,则第四点在这个圆上,此时这四个点共圆;
若第四点到圆心的距离不等于半径,则第四点不在这个圆上,此时这四个点不共圆。
点和圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d
作圆
过一点可以作无数个圆
过两点可以作无数个圆
不在同一直线上的三个点可确定一个圆
一个三角形的
外接圆是唯一的
注意:过同一直线上的三个点不能作圆
点 P 在圆环内
r≤d≤R
R
r
P
O
d
