27.2.2 直线与圆的位置关系(共20张PPT)2024-2025学年华师大版数学九年级下册
文档属性
| 名称 | 27.2.2 直线与圆的位置关系(共20张PPT)2024-2025学年华师大版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-07 11:35:27 | ||
图片预览






文档简介
(共20张PPT)
27.2.2 直线与圆的位置关系
1.理解直线与圆有相交、相切、相离三种位置关系,能根据圆心到直线的距离d和圆的半径r之间的数量关系,判断出直线与圆的位置关系.
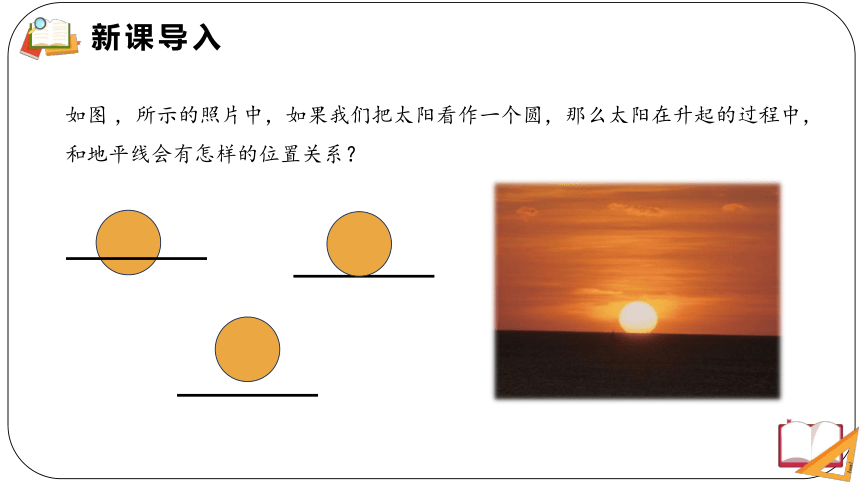
如图 ,所示的照片中,如果我们把太阳看作一个圆,那么太阳在升起的过程中,和地平线会有怎样的位置关系?
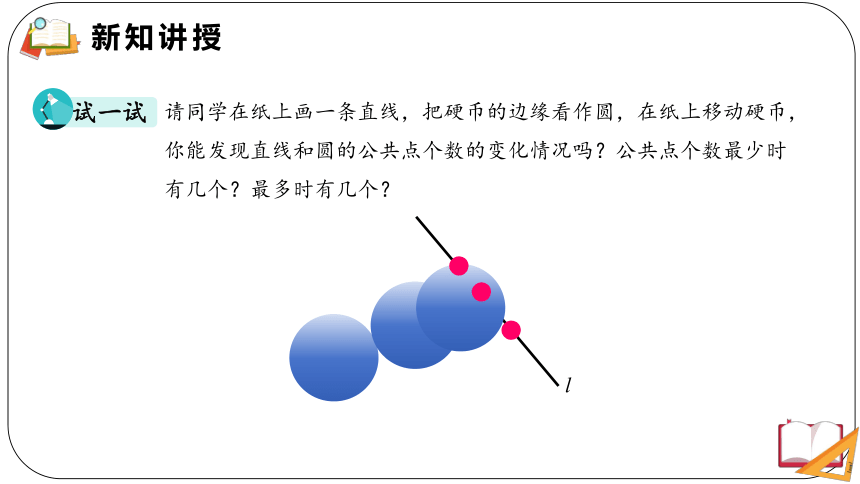
请同学在纸上画一条直线,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
l
●
●
●
试一试
直线与圆的位置关系
如果一条直线与一个圆没有公共点,那么就说这条直线与这个圆相离,如图所示.
概念生成
如果一条直线与一个圆只有一个公共点,那么就说这条直线与这个圆相切,如图所示.此时这条直线叫做圆的切线,这个公共点叫做切点.
●
概念生成
直线与圆的位置关系
如果一条直线与一个圆有两个公共点,那么就说这条直线与这个圆相交,如图所示.此时这条直线叫做圆的割线.
直线与圆的位置关系
概念生成
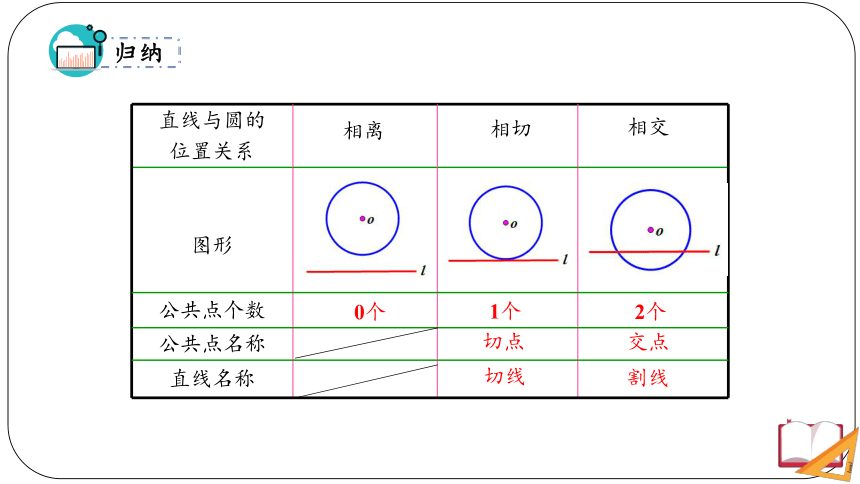
直线与圆的 位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
1个
切点
切线
0个
相离
相切
相交
割线
归纳
直线与圆最少有一个公共点. ( )
② 若直线与圆相交,则直线上的点都在圆上. ( )
③ 若 A 是☉O 上一点,则直线 AB 与☉O 相切. ( )
④ 若 C 为☉O 外一点,则过点 C 的直线与☉O 相交或相离. ( )
⑤ 直线 a 和☉O 有公共点,则直线 a 与☉O 相切.( )
×
×
×
×
×
判断正误:
小试牛刀
用数量关系判断直线与圆的位置关系
问题:同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
相关知识:
点到直线的距离是指从直线外一点 (A) 到直线 (l ) 的垂线段 (OA) 的长度.
圆心到直线的距离也在改变:
首先距离大于半径,
然后距离等于半径,
最后距离小于半径.
怎样用圆心到直线的距离 d 来判定直线 l 与 ⊙O 的位置关系呢?
O
d
l
思考
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
可以通过圆心O到直线的距离d与圆的半径r的关系来区分
o
o
o
公共点个数
B
C
A
8
6
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,以点C为圆心,分别以下面给出的r为半径作圆,试问所作的圆与斜边AB所在的直线分别有怎样的位置关系?请说明理由.
(1) r = 4;(2) r = 4.8; (3) r = 5.
分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出点C到AB的距离d.
B
C
A
8
6
D
解:过点C作CD⊥AB,垂足为D.
在△ABC中,
AB=
10.
根据三角形的面积公式有
即点C到直线AB的距离d=4.8.
(1)当r=4时,d >r,因此⊙C 与AB 相离;
(2)当r=4.8时,d =r,因此⊙C 与AB 相切;
(3)当r=5时,d <r,因此⊙C 与AB 相交.
∴
8
6
10
4.8.
1.如图是“光盘行动”的宣传海报,图中筷子与餐盘可看成直线和圆的位置关系是( )
A.相切
B.相交
C.相离
D.平行
B
2.已知平面内有⊙O和点A,B,若⊙O的半径为2 cm,线段OA=3 cm,OB=2 cm,则直线AB和⊙O的位置关系为( )
A.相离
B.相交
C.相切
D.相交或相切
D
3.已知⊙O的直径等于12 cm,圆心O到直线l的距离为5 cm,则直线l和⊙O的公共点个数为( )
A.0个
B.1个
C.2个
D.无法确定
C
4.如图,直线l是⊙O的切线,A为切点,B为直线l上一点,连结OB交⊙O于点C.若AB=12,OA=5,则BC的长为( )
A.5
B.6
C.7
D.8
D
图形
公共点个数
d与r的关系
直线与圆的 位置关系
公共点名称
直线名称
2 个
交点
割线
1 个
切点
切线
0 个
相离
相切
相交
dd=r
d>r
27.2.2 直线与圆的位置关系
1.理解直线与圆有相交、相切、相离三种位置关系,能根据圆心到直线的距离d和圆的半径r之间的数量关系,判断出直线与圆的位置关系.
如图 ,所示的照片中,如果我们把太阳看作一个圆,那么太阳在升起的过程中,和地平线会有怎样的位置关系?
请同学在纸上画一条直线,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
l
●
●
●
试一试
直线与圆的位置关系
如果一条直线与一个圆没有公共点,那么就说这条直线与这个圆相离,如图所示.
概念生成
如果一条直线与一个圆只有一个公共点,那么就说这条直线与这个圆相切,如图所示.此时这条直线叫做圆的切线,这个公共点叫做切点.
●
概念生成
直线与圆的位置关系
如果一条直线与一个圆有两个公共点,那么就说这条直线与这个圆相交,如图所示.此时这条直线叫做圆的割线.
直线与圆的位置关系
概念生成
直线与圆的 位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
1个
切点
切线
0个
相离
相切
相交
割线
归纳
直线与圆最少有一个公共点. ( )
② 若直线与圆相交,则直线上的点都在圆上. ( )
③ 若 A 是☉O 上一点,则直线 AB 与☉O 相切. ( )
④ 若 C 为☉O 外一点,则过点 C 的直线与☉O 相交或相离. ( )
⑤ 直线 a 和☉O 有公共点,则直线 a 与☉O 相切.( )
×
×
×
×
×
判断正误:
小试牛刀
用数量关系判断直线与圆的位置关系
问题:同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
相关知识:
点到直线的距离是指从直线外一点 (A) 到直线 (l ) 的垂线段 (OA) 的长度.
圆心到直线的距离也在改变:
首先距离大于半径,
然后距离等于半径,
最后距离小于半径.
怎样用圆心到直线的距离 d 来判定直线 l 与 ⊙O 的位置关系呢?
O
d
l
思考
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
可以通过圆心O到直线的距离d与圆的半径r的关系来区分
o
o
o
公共点个数
B
C
A
8
6
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,以点C为圆心,分别以下面给出的r为半径作圆,试问所作的圆与斜边AB所在的直线分别有怎样的位置关系?请说明理由.
(1) r = 4;(2) r = 4.8; (3) r = 5.
分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出点C到AB的距离d.
B
C
A
8
6
D
解:过点C作CD⊥AB,垂足为D.
在△ABC中,
AB=
10.
根据三角形的面积公式有
即点C到直线AB的距离d=4.8.
(1)当r=4时,d >r,因此⊙C 与AB 相离;
(2)当r=4.8时,d =r,因此⊙C 与AB 相切;
(3)当r=5时,d <r,因此⊙C 与AB 相交.
∴
8
6
10
4.8.
1.如图是“光盘行动”的宣传海报,图中筷子与餐盘可看成直线和圆的位置关系是( )
A.相切
B.相交
C.相离
D.平行
B
2.已知平面内有⊙O和点A,B,若⊙O的半径为2 cm,线段OA=3 cm,OB=2 cm,则直线AB和⊙O的位置关系为( )
A.相离
B.相交
C.相切
D.相交或相切
D
3.已知⊙O的直径等于12 cm,圆心O到直线l的距离为5 cm,则直线l和⊙O的公共点个数为( )
A.0个
B.1个
C.2个
D.无法确定
C
4.如图,直线l是⊙O的切线,A为切点,B为直线l上一点,连结OB交⊙O于点C.若AB=12,OA=5,则BC的长为( )
A.5
B.6
C.7
D.8
D
图形
公共点个数
d与r的关系
直线与圆的 位置关系
公共点名称
直线名称
2 个
交点
割线
1 个
切点
切线
0 个
相离
相切
相交
d
d>r
