2025年中考数学复习--线段有关的动点巩固练习一(含解析)
文档属性
| 名称 | 2025年中考数学复习--线段有关的动点巩固练习一(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 669.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 06:20:16 | ||
图片预览




文档简介
线段有关的动点巩固练习
【巩固练习1】
如图,四边形 ABCD 是菱形,对角线AC,BD 相交于点O,AC=6 ,BD=6,点 P 是AC上一动点,点E 是AB 的中点,则PD+PE 的最小值为( )
B.6
C.3
【巩固练习2】
如图,已知点 P 是菱形 ABCD 的对角线AC 延长线上一点,过点 P 分别作AD、DC 延长线的垂线,垂足分别为点 E、F.若∠ABC =120°,AB=2,则 PE-PF 的值为( )
A.
B.
C.2
D.
【巩固练习3】
如图,已知正方形ABCD 的边长为6,点 F是正方形内一点,连接 CF,DF,且∠ADF =∠DCF,点E 是AD 边上一动点,连接EB,EF,则 EB+EF 长度的最小值为 .
【巩固练习4】
如图,在 Rt△AOB 中,∠AOB =90°,OA =4,OB=6,以点O 为圆心,3为半径的⊙O,与OB 交于点 C,过点 C 作 CD⊥OB 交AB 于点D,点 P 是边 OA 上的点,则PC+PD 的最小值为 .
【巩固练习5】
如图,正方形ABCD 中,AB =1,连接AC,∠ACD 的平分线交 AD 于点 E,在AB 上截取AF=DE,连接 DF,分别交 CE,AC 于点 G,H,点 P 是线段 GC上的动点,PQ⊥AC 于点 Q,连接PH.下列结论:①CE⊥DF;②DE +DC =AC;③EA= AH ;④PH+PQ 的最小值是 其中所有正确结论的序号是 .
【巩固练习6】
如图,在平面直角坐标系中,矩形 OABC的两边OC、OA 分别在坐标轴上,且OA=2,OC=4,连接OB.反比例函数 的图象经过线段OB 的中点D,并与AB、BC 分别交于点E、F.一次函数. 的图象经过E、F 两点.
(1)分别求出一次函数和反比例函数的表达式;
(2)点P 是x轴上一动点,当PE+PF 的值最小时,点P 的坐标为 .
中小学教育资源及组卷应用平台
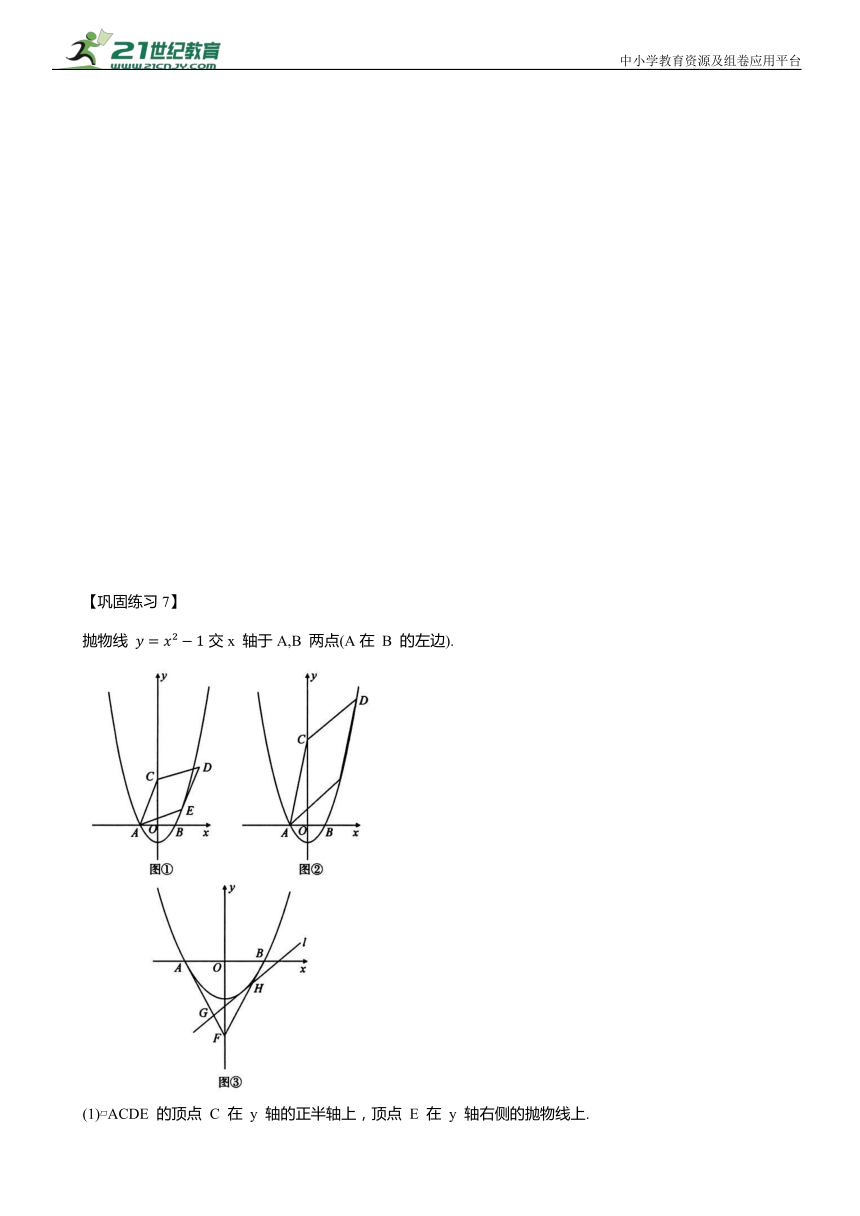
【巩固练习7】
抛物线 交x 轴于A,B 两点(A在 B 的左边).
(1) ACDE 的顶点 C 在 y 轴的正半轴上,顶点 E 在 y 轴右侧的抛物线上.
①如图①,若点 C 的坐标是(0,3),点 E的横坐标是 ,直接写出点A,D的坐标;
②如图②,若点 D 在抛物线上,且 ACDE的面积是12,求点 E 的坐标;
(2)如图③,F是原点 O 关于抛物线顶点的对称点,不平行y 轴的直线l 分别交线段AF,BF (不含端点)于 G,H 两点,若直线l与抛物线只有一个公共点,求证 FG+FH 的值是定值.
【巩固练习8】
如图,二次函数 是实数,且-1(1)求A、B、C三点的坐标(用数字或含 m的式子表示);
(2)已知点 Q 在抛物线的对称轴上,当△AFQ 的周长的最小值等于 时,求m 的值.
【巩固练习9】
如图,在△ABC 中,∠ACB =90°,AC =BC=4,点 D 是BC 边的中点,点 P 是AC 边上的一个动点,连接 PD,以 PD 为边在 PD 的下方作等边三角形 PDQ,连接CQ.则 CQ 的最小值是( )
B.1
D.
【巩固练习10】
如图,在△ABC 中,∠ABC =90°,AB =8,BC=12,D为AC边上的一个动点,连接BD,E为BD上的一个动点,连接AE,CE,当∠ABD =∠BCE时,线段AE 的最小值是( )
A.3 B.4
C.5 D.6
1.如图, 连接DE,
在 中,
∴当点P在DE上时, 的最小值为DE的长,
∵四边形ABCD是菱形,
是等边三角形,
∵点E是AB的中点,
故选: A.
2.设AC交BD于O, 如图:
∵在菱形ABCD中,
中,
中,
中,
故选: B.
3.∵四边形ABCD是正方形,
∴点F在以DC为直径的半圆上移动,
如图,设DC的中点为O,作正方形ABCD关于直线AD对称的正方形. 则点B的对应点是B',
连接 交AD于E,交半圆O于F,则线段 的长即为 的长度最小值,
的长度最小值为
4.答案
解析 如图,延长CO交⊙O于点E,连接ED,交AO于点 P,则此时 的值最小,最小值为线段 DE的长.
因为 所以 因为 所以 所以 所以 即 所以 在 中, 所以 的最小值为
5.∵正方形ABCD,
∴CD=AD, ∠CDE=∠DAF =90°,
∴∠ADF+∠CDF =90°,
在△CDE和△DAF中,
∴△CDE≌△DAF(ASA),
∴∠DCE=∠ADF,
∴∠DCF+∠CDF =90°,
∴∠DGC = 90°,
∴CE⊥DF, 故①正确;
∵CE平分∠ACD,
∴∠DCE=∠HCG,
在△GCD和△GCH中,
∴△GCD≌△GCH(ASA),
∴CD=CH, ∠CDH =∠CHD,
∵正方形ABCD,
∴CD∥AB,
∴∠CDF=∠AFD,
∴∠CHD=∠AFD,
∵∠CHD=∠AHF,
∴∠AFD=∠AHF,
∴AF=AH,
∴AC=AH+CH=AF+CD=DE+CD, 故②正确,设DE =AF = AH =a,
∵∠AHF =∠DHC, ∠CDF =∠AFH,
∴△DHC∽△FHA,
故③错误;
∵△GCD≌△GCH,
∴DG=GH,
∵CE⊥DF,
∴CG垂直平分DH,
∴DP=PH,
当DQ⊥HC时,. 有最小值,
过点D作DM⊥HC,
则DM的长度为PH+PQ的最小值,
故④正确.
故答案为: ①②④.
6.(1)∵四边形OABC为矩形,( ∴B(4,2).
由中点坐标公式可得点D坐标为(2,1),
∵反比例函数 的图象经过线段OB的中点D,
故反比例函数表达式为
令 则 令 则
故点E坐标为(1,2),
设直线EF的解析式为 代入E、F坐标得:
解得:
故一次函数的解析式为
(2)作点E关于x轴的对称点E',连接 交x轴于点P,则此时 最小.如图.
由E坐标可得对称点. 设直线 的解析式为 , 代入点E'、F坐标, 得:
解得:
则直线. 的解析式为
令 则
∴点P坐标为
故答案为:
7.(1) 对于 令 解得 令 则
故点A、B的坐标分别为( 顶点坐标为( ①当 时,
由点A、C的坐标知,点A向右平移1个单位向上平移3个单位得到点C,
∵四边形ACDE为平行四边形,
故点E向右平移1个单位向上平移3个单位得到点D,
则
故点D的坐标为
②设点C(0,n), 点E的坐标为(
同理可得,点D的坐标为
将点D的坐标代入抛物线表达式得:
解得
故点C的坐标为(
连接CE,过点E作y轴的平行线交x轴于点M,交过点C与x轴的平行线与点N,
则
解得 (舍去)或2,
故点E的坐标为(2,3);
(2)∵F是原点O关于抛物线顶点的对称点,故点F的坐标为
由点B、F的坐标得,直线BF的表达式为 同理可得,直线AF的表达式为 设直线l的表达式为
联立 和 并整理得: ,
∵直线l与抛物线只有一个公共点,
故 解得
故直线l的表达式为
联立①③并解得
同理可得,
∵射线FA、FB关于y轴对称, 则 设
则
则 为常数.
8.(1) 令 解得: 或m,故点A、B的坐标分别为(m,0)、(1,0),则点C的横坐标为 即点C的坐标为
(2)由点C的坐标知,
故
即
∵点C是OB的中点,则CD为三角形BOE的中位线,
则
在 中,
∵点B是点A关于函数对称轴的对称点,连接FB交对称轴于点
Q,则点Q为所求点,
理由: 的周长
为最小,即
则解得
故
9.解法一:如图在CD的下方作等边 作射线TQ.
在 和 中,
∴点Q在射线TQ上运动 (点T是定点, 是定值),当 时,CQ的值最小,最小值
10.如图, 取BC的中点T, 连接AT, ET.
∴AE的最小值为4,
故选: B.
【巩固练习1】
如图,四边形 ABCD 是菱形,对角线AC,BD 相交于点O,AC=6 ,BD=6,点 P 是AC上一动点,点E 是AB 的中点,则PD+PE 的最小值为( )
B.6
C.3
【巩固练习2】
如图,已知点 P 是菱形 ABCD 的对角线AC 延长线上一点,过点 P 分别作AD、DC 延长线的垂线,垂足分别为点 E、F.若∠ABC =120°,AB=2,则 PE-PF 的值为( )
A.
B.
C.2
D.
【巩固练习3】
如图,已知正方形ABCD 的边长为6,点 F是正方形内一点,连接 CF,DF,且∠ADF =∠DCF,点E 是AD 边上一动点,连接EB,EF,则 EB+EF 长度的最小值为 .
【巩固练习4】
如图,在 Rt△AOB 中,∠AOB =90°,OA =4,OB=6,以点O 为圆心,3为半径的⊙O,与OB 交于点 C,过点 C 作 CD⊥OB 交AB 于点D,点 P 是边 OA 上的点,则PC+PD 的最小值为 .
【巩固练习5】
如图,正方形ABCD 中,AB =1,连接AC,∠ACD 的平分线交 AD 于点 E,在AB 上截取AF=DE,连接 DF,分别交 CE,AC 于点 G,H,点 P 是线段 GC上的动点,PQ⊥AC 于点 Q,连接PH.下列结论:①CE⊥DF;②DE +DC =AC;③EA= AH ;④PH+PQ 的最小值是 其中所有正确结论的序号是 .
【巩固练习6】
如图,在平面直角坐标系中,矩形 OABC的两边OC、OA 分别在坐标轴上,且OA=2,OC=4,连接OB.反比例函数 的图象经过线段OB 的中点D,并与AB、BC 分别交于点E、F.一次函数. 的图象经过E、F 两点.
(1)分别求出一次函数和反比例函数的表达式;
(2)点P 是x轴上一动点,当PE+PF 的值最小时,点P 的坐标为 .
中小学教育资源及组卷应用平台
【巩固练习7】
抛物线 交x 轴于A,B 两点(A在 B 的左边).
(1) ACDE 的顶点 C 在 y 轴的正半轴上,顶点 E 在 y 轴右侧的抛物线上.
①如图①,若点 C 的坐标是(0,3),点 E的横坐标是 ,直接写出点A,D的坐标;
②如图②,若点 D 在抛物线上,且 ACDE的面积是12,求点 E 的坐标;
(2)如图③,F是原点 O 关于抛物线顶点的对称点,不平行y 轴的直线l 分别交线段AF,BF (不含端点)于 G,H 两点,若直线l与抛物线只有一个公共点,求证 FG+FH 的值是定值.
【巩固练习8】
如图,二次函数 是实数,且-1
(2)已知点 Q 在抛物线的对称轴上,当△AFQ 的周长的最小值等于 时,求m 的值.
【巩固练习9】
如图,在△ABC 中,∠ACB =90°,AC =BC=4,点 D 是BC 边的中点,点 P 是AC 边上的一个动点,连接 PD,以 PD 为边在 PD 的下方作等边三角形 PDQ,连接CQ.则 CQ 的最小值是( )
B.1
D.
【巩固练习10】
如图,在△ABC 中,∠ABC =90°,AB =8,BC=12,D为AC边上的一个动点,连接BD,E为BD上的一个动点,连接AE,CE,当∠ABD =∠BCE时,线段AE 的最小值是( )
A.3 B.4
C.5 D.6
1.如图, 连接DE,
在 中,
∴当点P在DE上时, 的最小值为DE的长,
∵四边形ABCD是菱形,
是等边三角形,
∵点E是AB的中点,
故选: A.
2.设AC交BD于O, 如图:
∵在菱形ABCD中,
中,
中,
中,
故选: B.
3.∵四边形ABCD是正方形,
∴点F在以DC为直径的半圆上移动,
如图,设DC的中点为O,作正方形ABCD关于直线AD对称的正方形. 则点B的对应点是B',
连接 交AD于E,交半圆O于F,则线段 的长即为 的长度最小值,
的长度最小值为
4.答案
解析 如图,延长CO交⊙O于点E,连接ED,交AO于点 P,则此时 的值最小,最小值为线段 DE的长.
因为 所以 因为 所以 所以 所以 即 所以 在 中, 所以 的最小值为
5.∵正方形ABCD,
∴CD=AD, ∠CDE=∠DAF =90°,
∴∠ADF+∠CDF =90°,
在△CDE和△DAF中,
∴△CDE≌△DAF(ASA),
∴∠DCE=∠ADF,
∴∠DCF+∠CDF =90°,
∴∠DGC = 90°,
∴CE⊥DF, 故①正确;
∵CE平分∠ACD,
∴∠DCE=∠HCG,
在△GCD和△GCH中,
∴△GCD≌△GCH(ASA),
∴CD=CH, ∠CDH =∠CHD,
∵正方形ABCD,
∴CD∥AB,
∴∠CDF=∠AFD,
∴∠CHD=∠AFD,
∵∠CHD=∠AHF,
∴∠AFD=∠AHF,
∴AF=AH,
∴AC=AH+CH=AF+CD=DE+CD, 故②正确,设DE =AF = AH =a,
∵∠AHF =∠DHC, ∠CDF =∠AFH,
∴△DHC∽△FHA,
故③错误;
∵△GCD≌△GCH,
∴DG=GH,
∵CE⊥DF,
∴CG垂直平分DH,
∴DP=PH,
当DQ⊥HC时,. 有最小值,
过点D作DM⊥HC,
则DM的长度为PH+PQ的最小值,
故④正确.
故答案为: ①②④.
6.(1)∵四边形OABC为矩形,( ∴B(4,2).
由中点坐标公式可得点D坐标为(2,1),
∵反比例函数 的图象经过线段OB的中点D,
故反比例函数表达式为
令 则 令 则
故点E坐标为(1,2),
设直线EF的解析式为 代入E、F坐标得:
解得:
故一次函数的解析式为
(2)作点E关于x轴的对称点E',连接 交x轴于点P,则此时 最小.如图.
由E坐标可得对称点. 设直线 的解析式为 , 代入点E'、F坐标, 得:
解得:
则直线. 的解析式为
令 则
∴点P坐标为
故答案为:
7.(1) 对于 令 解得 令 则
故点A、B的坐标分别为( 顶点坐标为( ①当 时,
由点A、C的坐标知,点A向右平移1个单位向上平移3个单位得到点C,
∵四边形ACDE为平行四边形,
故点E向右平移1个单位向上平移3个单位得到点D,
则
故点D的坐标为
②设点C(0,n), 点E的坐标为(
同理可得,点D的坐标为
将点D的坐标代入抛物线表达式得:
解得
故点C的坐标为(
连接CE,过点E作y轴的平行线交x轴于点M,交过点C与x轴的平行线与点N,
则
解得 (舍去)或2,
故点E的坐标为(2,3);
(2)∵F是原点O关于抛物线顶点的对称点,故点F的坐标为
由点B、F的坐标得,直线BF的表达式为 同理可得,直线AF的表达式为 设直线l的表达式为
联立 和 并整理得: ,
∵直线l与抛物线只有一个公共点,
故 解得
故直线l的表达式为
联立①③并解得
同理可得,
∵射线FA、FB关于y轴对称, 则 设
则
则 为常数.
8.(1) 令 解得: 或m,故点A、B的坐标分别为(m,0)、(1,0),则点C的横坐标为 即点C的坐标为
(2)由点C的坐标知,
故
即
∵点C是OB的中点,则CD为三角形BOE的中位线,
则
在 中,
∵点B是点A关于函数对称轴的对称点,连接FB交对称轴于点
Q,则点Q为所求点,
理由: 的周长
为最小,即
则解得
故
9.解法一:如图在CD的下方作等边 作射线TQ.
在 和 中,
∴点Q在射线TQ上运动 (点T是定点, 是定值),当 时,CQ的值最小,最小值
10.如图, 取BC的中点T, 连接AT, ET.
∴AE的最小值为4,
故选: B.
同课章节目录
