2025年中考数学复习--线段有关的动点巩固练习二(含解析)
文档属性
| 名称 | 2025年中考数学复习--线段有关的动点巩固练习二(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 874.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 00:00:00 | ||
图片预览



文档简介
线段有关的动点巩固练习
【巩固练习1】
如图,在正方形ABCD 中,AB =2,E 为边AB上一点,F 为边 BC 上一点.连接 DE 和AF交于点 G,连接 BG.若AE =BF,则 BG的最小值为 .
【巩固练习2】
在△ABC 中,∠ABC=90°,AB=2,BC=3.点 D 为平面上一个动点,∠ADB =45°,则线段CD 长度的最小值为 .
【巩固练习3】
如图,在 Rt△ABC 中,∠BAC =90°,AB =2 ,AC=6,点 E在线段AC 上,且AE=1,D是线段 BC 上的一点,连接 DE,将四边形ABDE 沿直线 DE 翻折,得到四边形 FGDE,当点 G恰好落在线段AC 上时,AF= .
中小学教育资源及组卷应用平台
【巩固练习4】
如图,正方形ABCD 的边长为4,⊙O 的半径为1.若⊙O 在正方形ABCD 内平移(⊙O 可以与该正方形的边相切),则点 A 到⊙O 上的点的距离最大值为 .
【巩固练习5】
在平面直角坐标系xOy 中,⊙O 的半径为1,对于点A 和线段 BC,给出如下定义:若将线段BC 绕点 A 旋转可以得到⊙O 的弦 B'C'(B',C' 分别是 B,C 的对应点),则称线段BC是⊙O 的以点 A 为中心的“关联线段”.
(1)如图,点A,B ,C ,B ,C ,B ,C 的横、纵坐标都是整数.在线段 B C ,B C ,B C 中,⊙O 的以点 A 为中心的“关联线段”是 ;
(2)△ABC 是边长为1的等边三角形,点A(0,t),其中t≠0.若BC 是⊙O 的以点A 为中心的“关联线段”,求t 的值;
(3)在△ABC 中,AB =1,AC=2.若 BC 是⊙O 的以点A 为中心的“关联线段”,直接写出OA 的最小值和最大值,以及相应的 BC 长.
【巩固练习6】
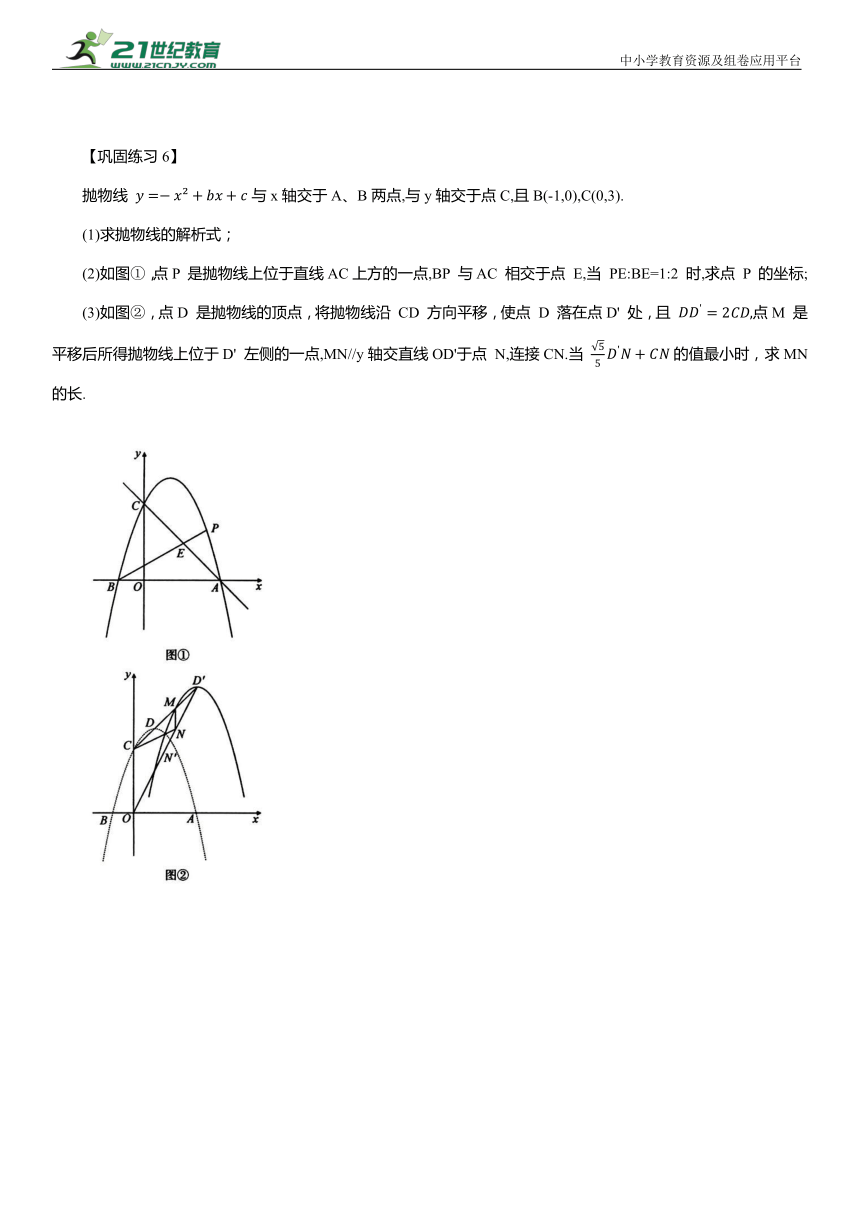
抛物线 与x轴交于A、B两点,与y轴交于点C,且B(-1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图①,点P 是抛物线上位于直线AC上方的一点,BP 与AC 相交于点 E,当 PE:BE=1:2 时,求点 P 的坐标;
(3)如图②,点D 是抛物线的顶点,将抛物线沿 CD 方向平移,使点 D 落在点D' 处,且 点M 是平移后所得抛物线上位于D' 左侧的一点,MN//y轴交直线OD'于点 N,连接CN.当 的值最小时,求MN的长.
【巩固练习7】
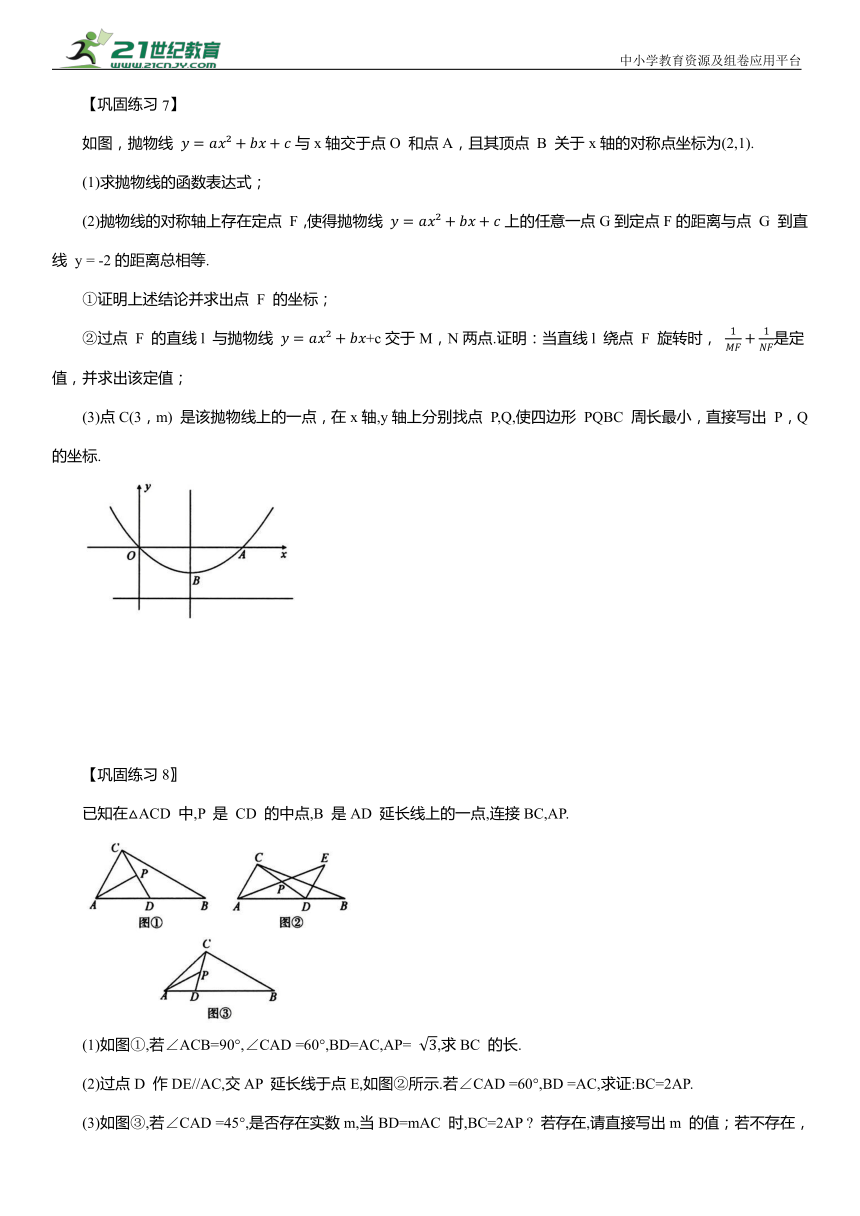
如图,抛物线 与x轴交于点O 和点A,且其顶点 B 关于x轴的对称点坐标为(2,1).
(1)求抛物线的函数表达式;
(2)抛物线的对称轴上存在定点 F,使得抛物线 上的任意一点G到定点F的距离与点 G 到直线 y = -2的距离总相等.
①证明上述结论并求出点 F 的坐标;
②过点 F 的直线l 与抛物线 +c交于M,N两点.证明:当直线l 绕点 F 旋转时, 是定值,并求出该定值;
(3)点C(3,m) 是该抛物线上的一点,在x轴,y轴上分别找点 P,Q,使四边形 PQBC 周长最小,直接写出 P,Q的坐标.
【巩固练习8〗
已知在△ACD 中,P 是 CD 的中点,B 是AD 延长线上的一点,连接BC,AP.
(1)如图①,若∠ACB=90°,∠CAD =60°,BD=AC,AP= ,求BC 的长.
(2)过点D 作DE//AC,交AP 延长线于点E,如图②所示.若∠CAD =60°,BD =AC,求证:BC=2AP.
(3)如图③,若∠CAD =45°,是否存在实数m,当BD=mAC 时,BC=2AP 若存在,请直接写出m 的值;若不存在,请说明理由.
【巩固练习9】
如图①,在四边形 ABCD 中,∠ABC =∠BCD,点E在边BC上,且AE//CD,DE//AB,作CF//AD 交线段AE 于点 F,连接BF.
(1)求证:△ABF≌△EAD;
(2)如图②,若AB =9,CD =5,∠ECF =∠AED,求BE的长;
(3)如图③,若BF的延长线经过AD 的中点M,求 的值.
【巩固练习10】
问题:如图,在 ABCD 中,AB=8,AD=5,∠DAB,∠ABC 的平分线 AE,BF 分别与直线CD交于点 E,F,求EF的长.
答案:EF=2.
探究:(1)把“问题”中的条件“AB=8 ”去掉,其余条件不变.
①当点 E 与点 F 重合时,求AB的长;
②当点 E 与点 C 重合时,求 EF的长.
(2)把“问题”中的条件“AB=8,AD=5 ”去掉,其余条件不变,当点C,D,E,F相邻两点间的距离相等时,求4D12的值.
【巩固练习11】
如图①,在平面直角坐标系 xOy 中,抛物线 与x轴分别相交于A、B两点,与y轴相交于点 C,下表给出了这条抛物线上部分点(x,y) 的坐标值:
x … -1 0 1 2 3
y … 0 3 4 3 0
(1)求出这条抛物线的解析式及顶点 M的坐标;
(2)PQ 是抛物线对称轴上长为1 的一条动线段(点 P 在点 Q 上方),求 AQ +QP +PC的最小值;
(3)如图②,点D 是第四象限内抛物线上一动点,过点D 作DF⊥x轴,垂足为F,△ABD的外接圆与 DF 相交于点 E.试问:线段 EF 的长是否为定值 如果是,请求出这个定值;如果不是,请说明理由.
1.如图, 取AD的中点T, 连接BT, GT.
∵四边形ABCD是正方形,
∴AD=BD=2, ∠DAE=∠ABE=90°,在△DAE和△ABF中,
∴△DAE≌△ABF(SAS),
∴∠ADE=∠BAF,
∵∠BAF+∠DAF =90°,
∴∠DAE+∠DAF=90°,
∴∠AGD=90°,
∵DT = AT,
∴BG≥BT-GT,
∴BG的最小值为
故答案为:
2.如图所示.
∵∠ADB=45°, AB =2, 作△ABD的外接圆O(因求CD最小值,故圆心O在AB的右侧),连接OC,当O、D、C三点共线时,CD的值最小.
∵∠ADB =45°,
∴∠AOB=90°,
∴△AOB为等腰直角三角形,
∵∠OBA =45°, ∠ABC = 90°,
∴∠OBE =45°, 作OE⊥BC于点E,
∴△OBE为等腰直角三角形.
∴OE = BE =sin45°·OB=1,
∴CE=BC--BE =3-1=2,
在Rt△OEC中,
当O、D、C三点共线时,
CD最小为(
故答案为:
3.如图,过点F作 于H,
∵将四边形ABDE沿直线DE翻折,得到四边形FGDE,
故答案为:
4.
设点 P是⊙O 上的任意一点,如图(1),连接OA,OP,AP,则点A到⊙O上的点的距离. ∴当OA取最大值时,AP 有最大值,为( .易知当⊙O 与 BC,CD 边相切时,OA取得最大值,如图(2),设⊙O与BC,CD边分别相切于点E,F,连接OE,OF,OC,易知四边形OECF是正方形,点A,O,C共线, 点A到⊙O 上的点的距离的最大值为
5.(1) 由旋转的性质可知:
由图可知点A到圆上一点的距离d的范围为
∴点 不可能在圆上,
不是⊙O的以A为中心的“关联线段”,
是⊙O的以A为中心的“关联线段”,
当 在圆上时, 或
由图可知此时 不在圆上,
不是⊙O的以A为中心的“关联线段”.
故答案为:
是边长为1的等边三角形,根据旋转的性质可知. 也是边长为1的等边三角形,
∵A(0,t),
轴,且
∴AO为 边上的高的2倍,且此高的长为
或
(3)OA的最小值为1时,此时BC的长为 ,OA的最大值为2,此时BC的长为
6.理由:由旋转的性质和“关联线段”的定义,
可知. 如图1,
利用四边形的不稳定性可知,
当A, O,( 在同一直线上时,OA最小,最小值为1,如图2,
此时
当A, B', O在同一直线上时, OA最大, 如图3,
此时( 过点A作 '于E, 过点( 作 于F.
综上OA的最小值为1,此时BC的长为 OA的最大值为2,此时BC的长为
7.经过
解得
∴抛物线的解析式为
(2)如图1中, 过点B作 轴交AC于T, 过点P作. 交AC于Q.
设.
对于抛物线 令 可得 或
∴A(3,0),
∵C(0,3),
∴直线AC的解析式为
解得 或2,
∴P(1,4)或(2,3).
(3)如图2中, 连接 过点N作 于J,过点C作 于T.
∴抛物线
∴顶点D(1,4),
∵C(0,3),
∴直线CD的解析式为
∵A(3,0),
轴,
的最小值为3,
此时N为( 与CT的交点,
∴N(1.5,3),
∵平移后抛物线的解析式为 MN平行y轴,将 代入抛物线解析式,
∴M(1.5,3.75),
8.(1)∵顶点B关于x轴的对称点坐标为(2,1),
∴A(4,0),
将点O、点A、点B代入抛物线
得到 解得
(2)①设F(2,m), G(x,y),
∴G点到直线 的距离为
,
∴G到直线 的距离与点(2,0)和G点的距离相等,
∴抛物线上的任意一点G到定点F的距离与点G到直线 的距离总相等;
∵G到定点F的距离与点G到直线 的距离相等,
整理得,
∵距离总相等,
∴F(2,0);
②设过点F的直线解析式为y= kx﹣2k, M(xM,yM), N(xN, yN),
联立 整理得
∵M到F点与M点到 的距离相等,N到F点与N点到 的距离相等,
是定值;
(3)作B点关于y轴的对称点, ,作C点关于x轴的对称点 连接 '交x轴、y轴分别于点P、 Q,
∴四边形PQBC周长
∵点C(3,m)是该抛物线上的一点
∴直线. 的解析为
9.(1)∵∠ACB=90°, ∠CAD=60°,
∵BD = AC,
∴AD=AC,
∴△ADC是等边三角形,
∴∠ACD=60°,
∵P是CD的中点,
∴AP⊥CD,
在Rt△APC中,
∴BC =AC×tan60°=2
(2)证明: 连接BE,
∵DE∥AC,
∴∠CAP=∠DEP,
在△CPA和△DPE中
∴△CPA≌△DPE(AAS),
∵BD=AC,
∴BD=DE,
又∵DE∥AC,
∴∠BDE=∠CAD=60°,
∴△BDE是等边三角形,
∴BD =BE, ∠EBD =60°,
∵BD=AC,
∴AC= BE,
在△CAB和△EBA中
∴△CAB≌△EBA(SAS),
∴AE=BC,
∴BC=2AP,
(3)存在这样的m,
理由如下: 作DE∥AC交AP延长线于E, 连接BE,由 (2) 同理可得DE=AC, ∠EDB=∠CAD=45°,AE=2AP,
当 时,
作BF⊥DE于F,
∵∠EDB=45°,
∴DE=DF,
∴点E, F重合,
∴∠BED=90°,
∴∠EBD=∠EDB=45°,
同 (2) 可证:
∴存在 使得
9. (1) ① 如图①,∵ 四边形 ABCD 是平行四边形,∴ CD=AB,BC=AD=5,AB∥CD.∴∠DEA=∠BAE.∵ AE 平分∠DAB,∴ ∠DAE=∠BAE.∴∠DEA=∠DAE.∴ DE=AD=5.同理,可得CF=BC=5.∵点E 与点F 重合,∴AB=CD=DE+CF=10 ② 如图②,∵ 点E 与点C 重合,∴ 易得DE=AD=5,CF=BC=5.∴点F与点D 重合.∴EF=DC=5 (2) 分三种情况讨论:① 如图③,由(1),可得AD=DE.∵点C、D、E、F 中相邻两点间的距离相等,∴ AD=DE=EF=CF.∴ 易得 ②如图④,由(1),可得AD=DE=CF.∵ DF=EF=CE,∴ 易得 ③如图⑤,由(1),可得AD=DE=CF.∵ DF=CD=CE,∴ 易得 综上所述, 的值为 或 或2
11.(1) 根据表格可得出A(--1,0), B(3,0), C(0,3),
设抛物线解析式为
将C(0,3)代入, 得:
解得:
∴该抛物线解析式为 顶点坐标为M(1,4);
(2)如图1,将点C沿y轴向下平移1个单位得( 连接 交抛物线对称轴: 于点
过点C作 交对称
轴于点. 连接
∵A、B关于直线 对称,
∴四边形( 是平行四边形,
在 中, )
此时, C'、Q'、B三点共线, 的值最小, 的最小值为
(3)线段EF的长为定值1.
如图2, 连接BE,设 且
轴,
∵F(t,0),
∵四边形ABED是圆内接四边形,
【巩固练习1】
如图,在正方形ABCD 中,AB =2,E 为边AB上一点,F 为边 BC 上一点.连接 DE 和AF交于点 G,连接 BG.若AE =BF,则 BG的最小值为 .
【巩固练习2】
在△ABC 中,∠ABC=90°,AB=2,BC=3.点 D 为平面上一个动点,∠ADB =45°,则线段CD 长度的最小值为 .
【巩固练习3】
如图,在 Rt△ABC 中,∠BAC =90°,AB =2 ,AC=6,点 E在线段AC 上,且AE=1,D是线段 BC 上的一点,连接 DE,将四边形ABDE 沿直线 DE 翻折,得到四边形 FGDE,当点 G恰好落在线段AC 上时,AF= .
中小学教育资源及组卷应用平台
【巩固练习4】
如图,正方形ABCD 的边长为4,⊙O 的半径为1.若⊙O 在正方形ABCD 内平移(⊙O 可以与该正方形的边相切),则点 A 到⊙O 上的点的距离最大值为 .
【巩固练习5】
在平面直角坐标系xOy 中,⊙O 的半径为1,对于点A 和线段 BC,给出如下定义:若将线段BC 绕点 A 旋转可以得到⊙O 的弦 B'C'(B',C' 分别是 B,C 的对应点),则称线段BC是⊙O 的以点 A 为中心的“关联线段”.
(1)如图,点A,B ,C ,B ,C ,B ,C 的横、纵坐标都是整数.在线段 B C ,B C ,B C 中,⊙O 的以点 A 为中心的“关联线段”是 ;
(2)△ABC 是边长为1的等边三角形,点A(0,t),其中t≠0.若BC 是⊙O 的以点A 为中心的“关联线段”,求t 的值;
(3)在△ABC 中,AB =1,AC=2.若 BC 是⊙O 的以点A 为中心的“关联线段”,直接写出OA 的最小值和最大值,以及相应的 BC 长.
【巩固练习6】
抛物线 与x轴交于A、B两点,与y轴交于点C,且B(-1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图①,点P 是抛物线上位于直线AC上方的一点,BP 与AC 相交于点 E,当 PE:BE=1:2 时,求点 P 的坐标;
(3)如图②,点D 是抛物线的顶点,将抛物线沿 CD 方向平移,使点 D 落在点D' 处,且 点M 是平移后所得抛物线上位于D' 左侧的一点,MN//y轴交直线OD'于点 N,连接CN.当 的值最小时,求MN的长.
【巩固练习7】
如图,抛物线 与x轴交于点O 和点A,且其顶点 B 关于x轴的对称点坐标为(2,1).
(1)求抛物线的函数表达式;
(2)抛物线的对称轴上存在定点 F,使得抛物线 上的任意一点G到定点F的距离与点 G 到直线 y = -2的距离总相等.
①证明上述结论并求出点 F 的坐标;
②过点 F 的直线l 与抛物线 +c交于M,N两点.证明:当直线l 绕点 F 旋转时, 是定值,并求出该定值;
(3)点C(3,m) 是该抛物线上的一点,在x轴,y轴上分别找点 P,Q,使四边形 PQBC 周长最小,直接写出 P,Q的坐标.
【巩固练习8〗
已知在△ACD 中,P 是 CD 的中点,B 是AD 延长线上的一点,连接BC,AP.
(1)如图①,若∠ACB=90°,∠CAD =60°,BD=AC,AP= ,求BC 的长.
(2)过点D 作DE//AC,交AP 延长线于点E,如图②所示.若∠CAD =60°,BD =AC,求证:BC=2AP.
(3)如图③,若∠CAD =45°,是否存在实数m,当BD=mAC 时,BC=2AP 若存在,请直接写出m 的值;若不存在,请说明理由.
【巩固练习9】
如图①,在四边形 ABCD 中,∠ABC =∠BCD,点E在边BC上,且AE//CD,DE//AB,作CF//AD 交线段AE 于点 F,连接BF.
(1)求证:△ABF≌△EAD;
(2)如图②,若AB =9,CD =5,∠ECF =∠AED,求BE的长;
(3)如图③,若BF的延长线经过AD 的中点M,求 的值.
【巩固练习10】
问题:如图,在 ABCD 中,AB=8,AD=5,∠DAB,∠ABC 的平分线 AE,BF 分别与直线CD交于点 E,F,求EF的长.
答案:EF=2.
探究:(1)把“问题”中的条件“AB=8 ”去掉,其余条件不变.
①当点 E 与点 F 重合时,求AB的长;
②当点 E 与点 C 重合时,求 EF的长.
(2)把“问题”中的条件“AB=8,AD=5 ”去掉,其余条件不变,当点C,D,E,F相邻两点间的距离相等时,求4D12的值.
【巩固练习11】
如图①,在平面直角坐标系 xOy 中,抛物线 与x轴分别相交于A、B两点,与y轴相交于点 C,下表给出了这条抛物线上部分点(x,y) 的坐标值:
x … -1 0 1 2 3
y … 0 3 4 3 0
(1)求出这条抛物线的解析式及顶点 M的坐标;
(2)PQ 是抛物线对称轴上长为1 的一条动线段(点 P 在点 Q 上方),求 AQ +QP +PC的最小值;
(3)如图②,点D 是第四象限内抛物线上一动点,过点D 作DF⊥x轴,垂足为F,△ABD的外接圆与 DF 相交于点 E.试问:线段 EF 的长是否为定值 如果是,请求出这个定值;如果不是,请说明理由.
1.如图, 取AD的中点T, 连接BT, GT.
∵四边形ABCD是正方形,
∴AD=BD=2, ∠DAE=∠ABE=90°,在△DAE和△ABF中,
∴△DAE≌△ABF(SAS),
∴∠ADE=∠BAF,
∵∠BAF+∠DAF =90°,
∴∠DAE+∠DAF=90°,
∴∠AGD=90°,
∵DT = AT,
∴BG≥BT-GT,
∴BG的最小值为
故答案为:
2.如图所示.
∵∠ADB=45°, AB =2, 作△ABD的外接圆O(因求CD最小值,故圆心O在AB的右侧),连接OC,当O、D、C三点共线时,CD的值最小.
∵∠ADB =45°,
∴∠AOB=90°,
∴△AOB为等腰直角三角形,
∵∠OBA =45°, ∠ABC = 90°,
∴∠OBE =45°, 作OE⊥BC于点E,
∴△OBE为等腰直角三角形.
∴OE = BE =sin45°·OB=1,
∴CE=BC--BE =3-1=2,
在Rt△OEC中,
当O、D、C三点共线时,
CD最小为(
故答案为:
3.如图,过点F作 于H,
∵将四边形ABDE沿直线DE翻折,得到四边形FGDE,
故答案为:
4.
设点 P是⊙O 上的任意一点,如图(1),连接OA,OP,AP,则点A到⊙O上的点的距离. ∴当OA取最大值时,AP 有最大值,为( .易知当⊙O 与 BC,CD 边相切时,OA取得最大值,如图(2),设⊙O与BC,CD边分别相切于点E,F,连接OE,OF,OC,易知四边形OECF是正方形,点A,O,C共线, 点A到⊙O 上的点的距离的最大值为
5.(1) 由旋转的性质可知:
由图可知点A到圆上一点的距离d的范围为
∴点 不可能在圆上,
不是⊙O的以A为中心的“关联线段”,
是⊙O的以A为中心的“关联线段”,
当 在圆上时, 或
由图可知此时 不在圆上,
不是⊙O的以A为中心的“关联线段”.
故答案为:
是边长为1的等边三角形,根据旋转的性质可知. 也是边长为1的等边三角形,
∵A(0,t),
轴,且
∴AO为 边上的高的2倍,且此高的长为
或
(3)OA的最小值为1时,此时BC的长为 ,OA的最大值为2,此时BC的长为
6.理由:由旋转的性质和“关联线段”的定义,
可知. 如图1,
利用四边形的不稳定性可知,
当A, O,( 在同一直线上时,OA最小,最小值为1,如图2,
此时
当A, B', O在同一直线上时, OA最大, 如图3,
此时( 过点A作 '于E, 过点( 作 于F.
综上OA的最小值为1,此时BC的长为 OA的最大值为2,此时BC的长为
7.经过
解得
∴抛物线的解析式为
(2)如图1中, 过点B作 轴交AC于T, 过点P作. 交AC于Q.
设.
对于抛物线 令 可得 或
∴A(3,0),
∵C(0,3),
∴直线AC的解析式为
解得 或2,
∴P(1,4)或(2,3).
(3)如图2中, 连接 过点N作 于J,过点C作 于T.
∴抛物线
∴顶点D(1,4),
∵C(0,3),
∴直线CD的解析式为
∵A(3,0),
轴,
的最小值为3,
此时N为( 与CT的交点,
∴N(1.5,3),
∵平移后抛物线的解析式为 MN平行y轴,将 代入抛物线解析式,
∴M(1.5,3.75),
8.(1)∵顶点B关于x轴的对称点坐标为(2,1),
∴A(4,0),
将点O、点A、点B代入抛物线
得到 解得
(2)①设F(2,m), G(x,y),
∴G点到直线 的距离为
,
∴G到直线 的距离与点(2,0)和G点的距离相等,
∴抛物线上的任意一点G到定点F的距离与点G到直线 的距离总相等;
∵G到定点F的距离与点G到直线 的距离相等,
整理得,
∵距离总相等,
∴F(2,0);
②设过点F的直线解析式为y= kx﹣2k, M(xM,yM), N(xN, yN),
联立 整理得
∵M到F点与M点到 的距离相等,N到F点与N点到 的距离相等,
是定值;
(3)作B点关于y轴的对称点, ,作C点关于x轴的对称点 连接 '交x轴、y轴分别于点P、 Q,
∴四边形PQBC周长
∵点C(3,m)是该抛物线上的一点
∴直线. 的解析为
9.(1)∵∠ACB=90°, ∠CAD=60°,
∵BD = AC,
∴AD=AC,
∴△ADC是等边三角形,
∴∠ACD=60°,
∵P是CD的中点,
∴AP⊥CD,
在Rt△APC中,
∴BC =AC×tan60°=2
(2)证明: 连接BE,
∵DE∥AC,
∴∠CAP=∠DEP,
在△CPA和△DPE中
∴△CPA≌△DPE(AAS),
∵BD=AC,
∴BD=DE,
又∵DE∥AC,
∴∠BDE=∠CAD=60°,
∴△BDE是等边三角形,
∴BD =BE, ∠EBD =60°,
∵BD=AC,
∴AC= BE,
在△CAB和△EBA中
∴△CAB≌△EBA(SAS),
∴AE=BC,
∴BC=2AP,
(3)存在这样的m,
理由如下: 作DE∥AC交AP延长线于E, 连接BE,由 (2) 同理可得DE=AC, ∠EDB=∠CAD=45°,AE=2AP,
当 时,
作BF⊥DE于F,
∵∠EDB=45°,
∴DE=DF,
∴点E, F重合,
∴∠BED=90°,
∴∠EBD=∠EDB=45°,
同 (2) 可证:
∴存在 使得
9. (1) ① 如图①,∵ 四边形 ABCD 是平行四边形,∴ CD=AB,BC=AD=5,AB∥CD.∴∠DEA=∠BAE.∵ AE 平分∠DAB,∴ ∠DAE=∠BAE.∴∠DEA=∠DAE.∴ DE=AD=5.同理,可得CF=BC=5.∵点E 与点F 重合,∴AB=CD=DE+CF=10 ② 如图②,∵ 点E 与点C 重合,∴ 易得DE=AD=5,CF=BC=5.∴点F与点D 重合.∴EF=DC=5 (2) 分三种情况讨论:① 如图③,由(1),可得AD=DE.∵点C、D、E、F 中相邻两点间的距离相等,∴ AD=DE=EF=CF.∴ 易得 ②如图④,由(1),可得AD=DE=CF.∵ DF=EF=CE,∴ 易得 ③如图⑤,由(1),可得AD=DE=CF.∵ DF=CD=CE,∴ 易得 综上所述, 的值为 或 或2
11.(1) 根据表格可得出A(--1,0), B(3,0), C(0,3),
设抛物线解析式为
将C(0,3)代入, 得:
解得:
∴该抛物线解析式为 顶点坐标为M(1,4);
(2)如图1,将点C沿y轴向下平移1个单位得( 连接 交抛物线对称轴: 于点
过点C作 交对称
轴于点. 连接
∵A、B关于直线 对称,
∴四边形( 是平行四边形,
在 中, )
此时, C'、Q'、B三点共线, 的值最小, 的最小值为
(3)线段EF的长为定值1.
如图2, 连接BE,设 且
轴,
∵F(t,0),
∵四边形ABED是圆内接四边形,
同课章节目录
