2025年中考数学复习-因动点产生的面积问题巩固练习(含解析)
文档属性
| 名称 | 2025年中考数学复习-因动点产生的面积问题巩固练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 563.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 00:00:00 | ||
图片预览

文档简介
因动点产生的面积问题巩固练习
【巩固练习1】
如图①,在△ABC中,AB=BC,BD⊥AC 于点D(AD>BD).动点 M 从A 点出发,沿折线AB→BC 方向运动,运动到点 C 停止.设点 M的运动路程为x,△AMD 的面积为y,y 与x的函数图象如图②,则AC 的长为( )
A.3 B.6
C.8 D.9
【巩固练习2】
如图,矩形纸片ABCD,AB =4,BC =8,点M、N分别在矩形的边AD、BC 上,将矩形纸片沿直线MN 折叠,使点 C落在矩形的边AD上,记为点 P,点 D 落在G处,连接PC,交 MN 于点Q,连接CM.下列结论:①四边形 CMPN 是菱形;②点 P 与点A 重合时,MN=5;③△PQM的面积S的取值范围是4≤S≤5.其中所有正确结论的序号是( )
A.①②③ B.①②
C.①③ D.②③
【巩固练习3】
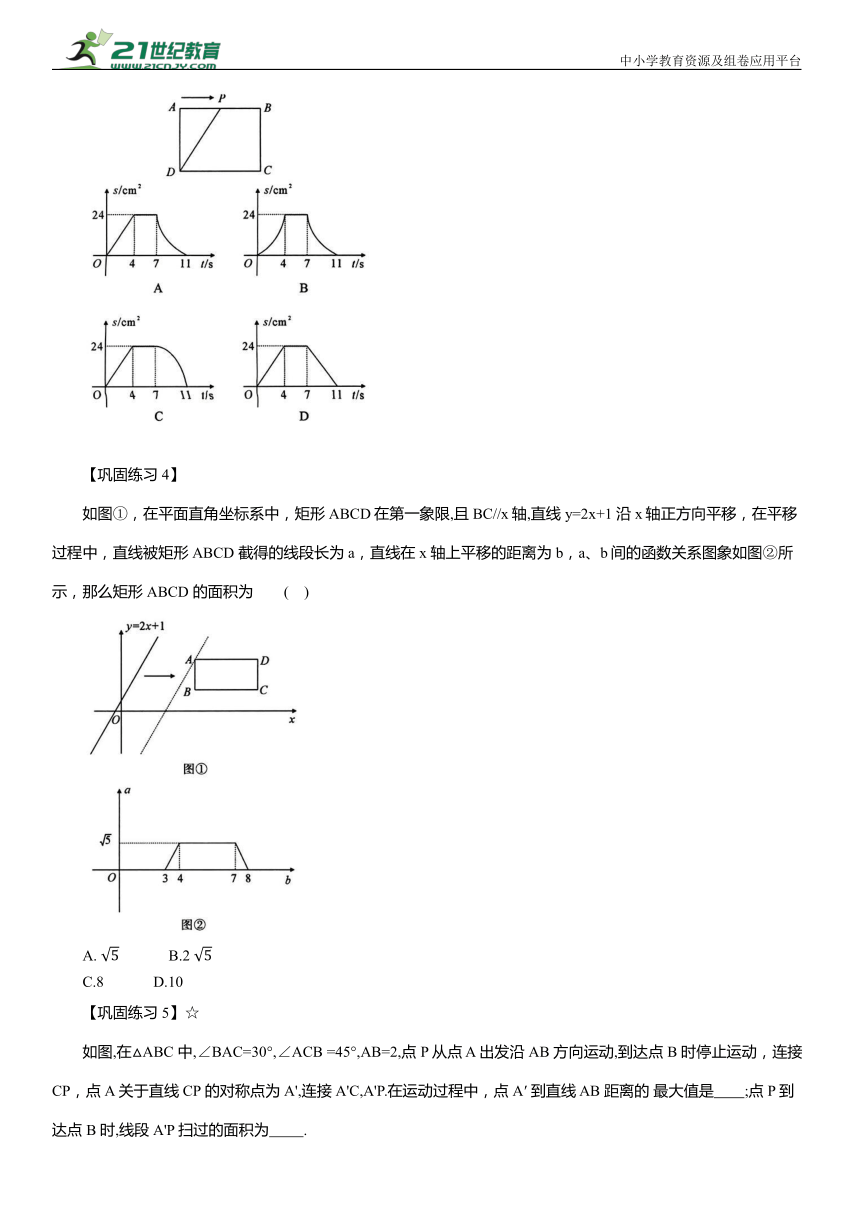
如图,在矩形 ABCD 中,AB =8cm ,AD =6 cm.点 P 从点 A 出发,以2cm /s的速度在矩形的边上沿A→B→C→D 运动,当点 P 与点D 重合时停止运动.设运动的时间为t(单位:s),△APD 的面积为S(单位:cm ),则 S随t变化的函数图象大致为( )
【巩固练习4】
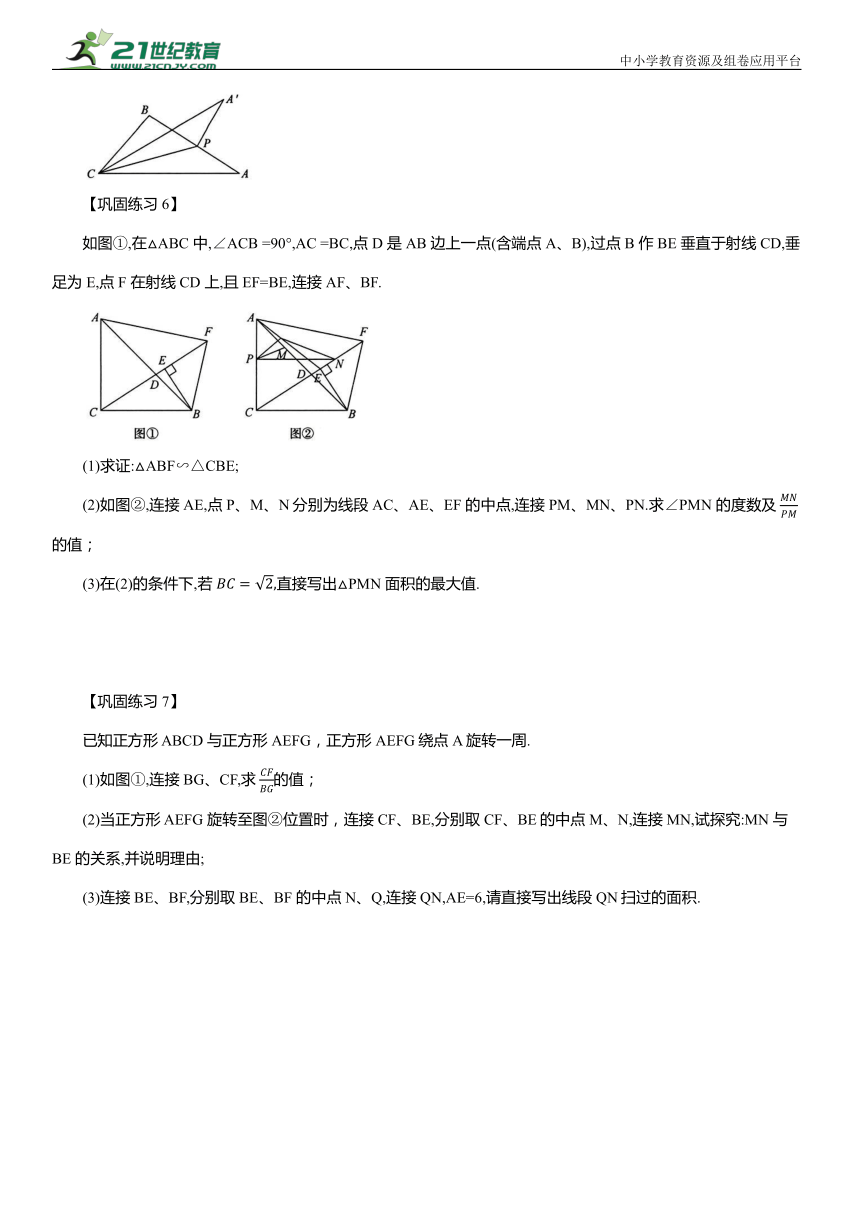
如图①,在平面直角坐标系中,矩形ABCD在第一象限,且BC//x轴,直线y=2x+1 沿x轴正方向平移,在平移过程中,直线被矩形ABCD 截得的线段长为a,直线在x 轴上平移的距离为b,a、b间的函数关系图象如图②所示,那么矩形ABCD 的面积为 ( )
A. B.2
C.8 D.10
【巩固练习5】☆
如图,在△ABC 中,∠BAC=30°,∠ACB =45°,AB=2,点 P 从点 A 出发沿AB 方向运动,到达点 B 时停止运动,连接CP,点A 关于直线CP 的对称点为A',连接A'C,A'P.在运动过程中,点A′ 到直线 AB 距离的 最大值是 ;点P 到达点 B 时,线段A'P扫过的面积为 .
【巩固练习6】
如图①,在△ABC 中,∠ACB =90°,AC =BC,点 D 是AB 边上一点(含端点A、B),过点B 作BE 垂直于射线 CD,垂足为 E,点 F 在射线CD 上,且EF=BE,连接AF、BF.
(1)求证:△ABF∽△CBE;
(2)如图②,连接AE,点 P、M、N分别为线段AC、AE、EF 的中点,连接 PM、MN、PN.求∠PMN 的度数及 的值;
(3)在(2)的条件下,若 直接写出△PMN 面积的最大值.
【巩固练习7】
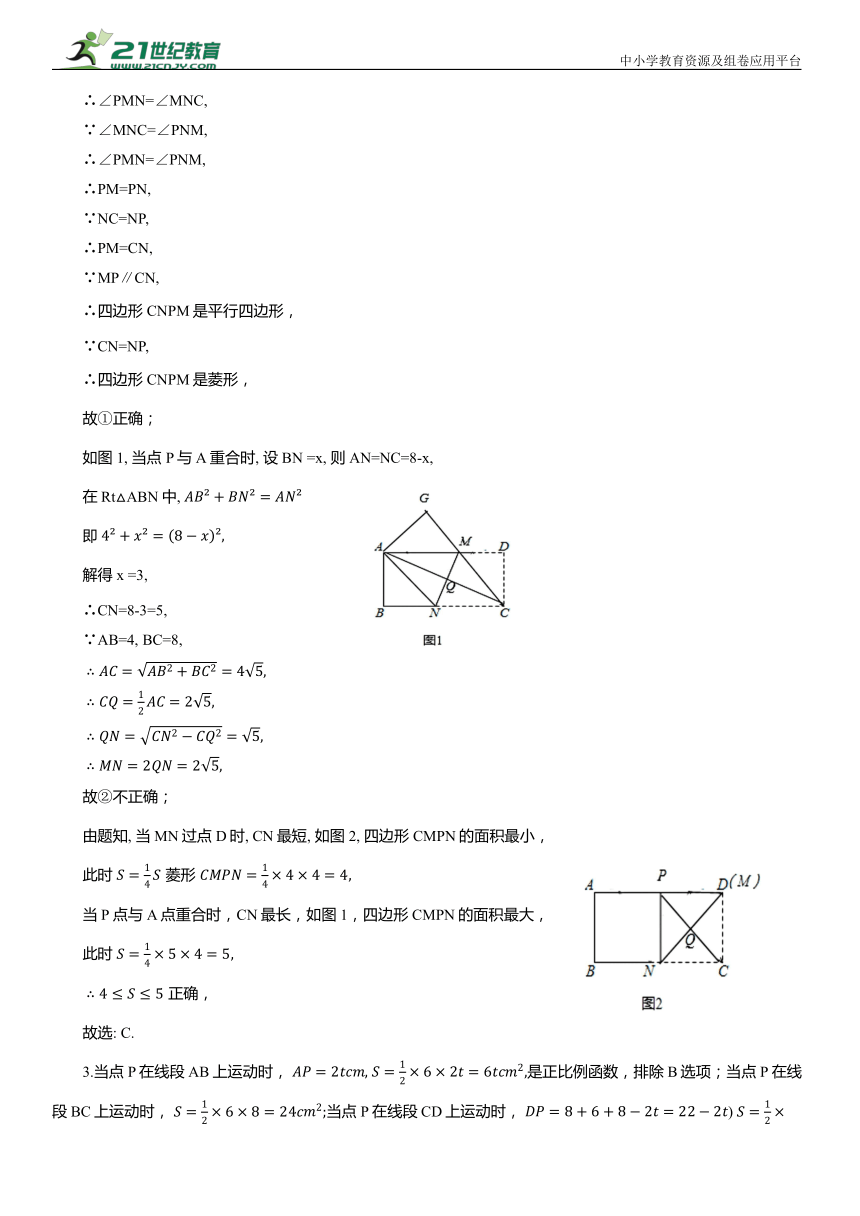
已知正方形 ABCD 与正方形AEFG,正方形AEFG绕点A 旋转一周.
(1)如图①,连接BG、CF,求 的值;
(2)当正方形 AEFG 旋转至图②位置时,连接CF、BE,分别取CF、BE的中点M、N,连接MN,试探究:MN 与 BE 的关系,并说明理由;
(3)连接BE、BF,分别取 BE、BF 的中点N、Q,连接QN,AE=6,请直接写出线段 QN扫过的面积.
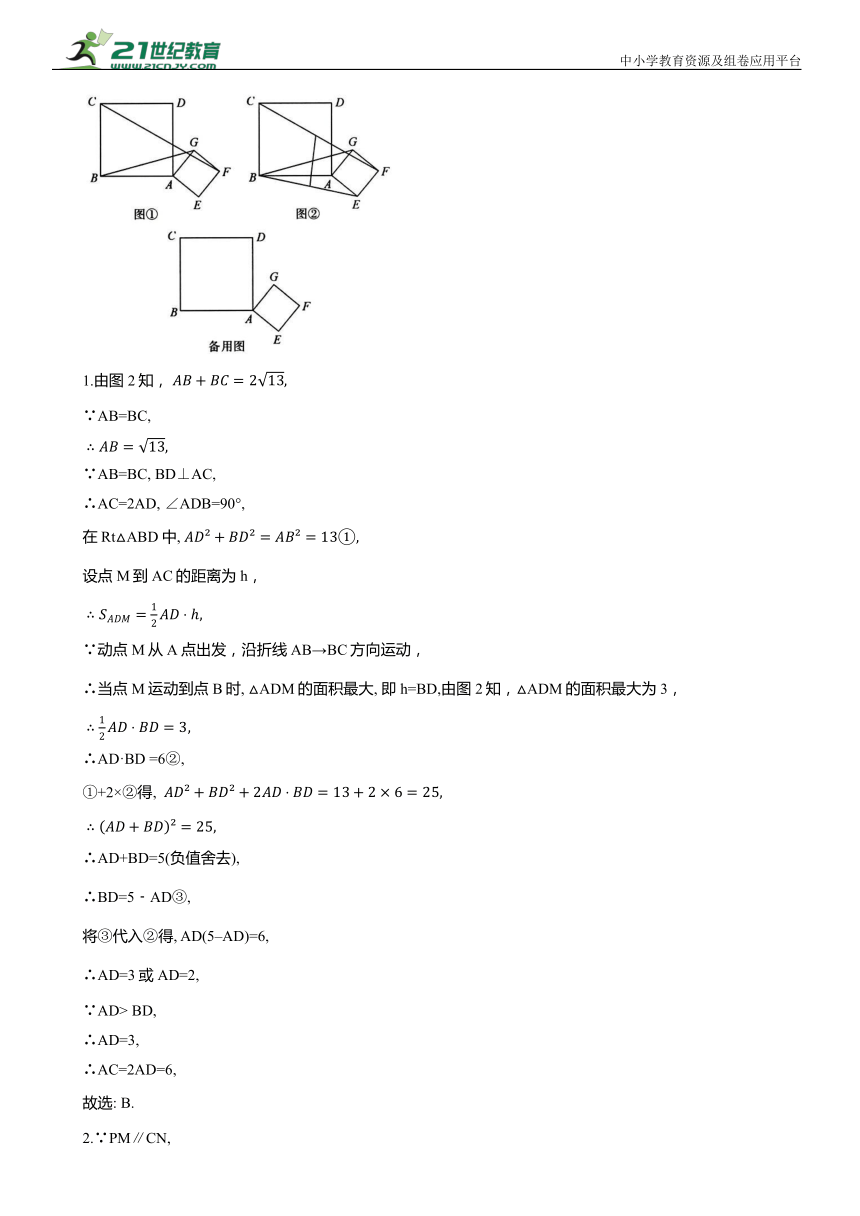
1.由图2知,
∵AB=BC,
∵AB=BC, BD⊥AC,
∴AC=2AD, ∠ADB=90°,
在Rt△ABD中,
设点M到AC的距离为h,
∵动点M从A点出发,沿折线AB→BC方向运动,
∴当点M运动到点B时, △ADM的面积最大, 即h=BD,由图2知,△ADM的面积最大为3,
∴AD·BD =6②,
①+2×②得,
∴AD+BD=5(负值舍去),
∴BD=5﹣AD③,
将③代入②得, AD(5–AD)=6,
∴AD=3或AD=2,
∵AD> BD,
∴AD=3,
∴AC=2AD=6,
故选: B.
2.∵PM∥CN,
∴∠PMN=∠MNC,
∵∠MNC=∠PNM,
∴∠PMN=∠PNM,
∴PM=PN,
∵NC=NP,
∴PM=CN,
∵MP∥CN,
∴四边形CNPM是平行四边形,
∵CN=NP,
∴四边形CNPM是菱形,
故①正确;
如图1, 当点P与A重合时, 设BN =x, 则AN=NC=8-x,
在Rt△ABN中,
即
解得x =3,
∴CN=8-3=5,
∵AB=4, BC=8,
故②不正确;
由题知, 当MN过点D时, CN最短, 如图2, 四边形CMPN的面积最小,
此时 菱形
当P点与A点重合时,CN最长,如图1,四边形CMPN的面积最大,
此时
正确,
故选: C.
3.当点P在线段AB上运动时, 是正比例函数,排除B选项;当点P在线段BC上运动时, 当点P在线段CD上运动时, ) ,是一次函数的图象,排除A,C选项,D选项符合题意;故选: D.
4.如图所示,过点B、D分别作 的平行线,交AD、BC于点E、F.
由图象和题意可得.
,
则
∴矩形ABCD的面积为
故答案为:8.
5.如图1中,过点B作 于H.
在 中,
在 中,
当 时, 点. 到直线AB的距离最大,设CA'交AB的延长线于K.
在 中,
如图2中,点P到达点B时,线段 扫过的面积
故答案为:
6.(1)证明: 如图1中,
(2)如图2中, 延长PM交AF于T.
中小学教育资源及组卷应用平台
∴四边形MNFT是平行四边形,
∴当EC的值最大时,PM的值最大,
∵当点E与B重合时,EC的值最大,EC的最大值为 此时
7.(1) 如图①, 连接AF, AC,
∵四边形ABCD和四边形AEFG都是正方形,
理由如下:如图②,连接ME,过点C作( 交直线ME于H, 连接BH, 设CF与AD交点为P, CF与AG交点为R,
∵CH∥EF,
∴∠FCH=∠CFE,
∵点M是CF的中点,
∴CM=MF,
又∵∠CMH=∠FME,
∴△CMH≌△FME(ASA),
∴CH=EF, ME=HM,
∴AE=CH,
∵CH∥EF,AG∥EF,
∴CH∥AG,
∴∠HCF =∠CRA,
∵AD∥BC,
∴∠BCF=∠APR,
∴∠BCH=∠BCF+∠HCF=∠APR+∠ARC,
∵∠DAG+∠APR+∠ARC =180°,
∠BAE+∠DAG=180°,
∴∠BAE=∠BCH,
又∵BC =AB, CH = AE,
∴△BCH≌△BAE(SAS),
∴BH = BE, ∠CBH =∠ABE,
∴∠HBE=∠CBA=90°,
∵MH = ME, 点N是BE中点,
∴BH=2MN,MN∥BH,
∴BE=2MN, MN⊥BE;
(3)如图③, 取AB中点O, 连接ON, OQ, AF,
∵点N是BE的中点,点Q是BF的中点,点O是AB的中点,
∴点Q在以点O为圆心, 为半径的圆上运动,点N在以点O为圆心,3为半径的圆上运动,
∴线段QN扫过的面积=
【巩固练习1】
如图①,在△ABC中,AB=BC,BD⊥AC 于点D(AD>BD).动点 M 从A 点出发,沿折线AB→BC 方向运动,运动到点 C 停止.设点 M的运动路程为x,△AMD 的面积为y,y 与x的函数图象如图②,则AC 的长为( )
A.3 B.6
C.8 D.9
【巩固练习2】
如图,矩形纸片ABCD,AB =4,BC =8,点M、N分别在矩形的边AD、BC 上,将矩形纸片沿直线MN 折叠,使点 C落在矩形的边AD上,记为点 P,点 D 落在G处,连接PC,交 MN 于点Q,连接CM.下列结论:①四边形 CMPN 是菱形;②点 P 与点A 重合时,MN=5;③△PQM的面积S的取值范围是4≤S≤5.其中所有正确结论的序号是( )
A.①②③ B.①②
C.①③ D.②③
【巩固练习3】
如图,在矩形 ABCD 中,AB =8cm ,AD =6 cm.点 P 从点 A 出发,以2cm /s的速度在矩形的边上沿A→B→C→D 运动,当点 P 与点D 重合时停止运动.设运动的时间为t(单位:s),△APD 的面积为S(单位:cm ),则 S随t变化的函数图象大致为( )
【巩固练习4】
如图①,在平面直角坐标系中,矩形ABCD在第一象限,且BC//x轴,直线y=2x+1 沿x轴正方向平移,在平移过程中,直线被矩形ABCD 截得的线段长为a,直线在x 轴上平移的距离为b,a、b间的函数关系图象如图②所示,那么矩形ABCD 的面积为 ( )
A. B.2
C.8 D.10
【巩固练习5】☆
如图,在△ABC 中,∠BAC=30°,∠ACB =45°,AB=2,点 P 从点 A 出发沿AB 方向运动,到达点 B 时停止运动,连接CP,点A 关于直线CP 的对称点为A',连接A'C,A'P.在运动过程中,点A′ 到直线 AB 距离的 最大值是 ;点P 到达点 B 时,线段A'P扫过的面积为 .
【巩固练习6】
如图①,在△ABC 中,∠ACB =90°,AC =BC,点 D 是AB 边上一点(含端点A、B),过点B 作BE 垂直于射线 CD,垂足为 E,点 F 在射线CD 上,且EF=BE,连接AF、BF.
(1)求证:△ABF∽△CBE;
(2)如图②,连接AE,点 P、M、N分别为线段AC、AE、EF 的中点,连接 PM、MN、PN.求∠PMN 的度数及 的值;
(3)在(2)的条件下,若 直接写出△PMN 面积的最大值.
【巩固练习7】
已知正方形 ABCD 与正方形AEFG,正方形AEFG绕点A 旋转一周.
(1)如图①,连接BG、CF,求 的值;
(2)当正方形 AEFG 旋转至图②位置时,连接CF、BE,分别取CF、BE的中点M、N,连接MN,试探究:MN 与 BE 的关系,并说明理由;
(3)连接BE、BF,分别取 BE、BF 的中点N、Q,连接QN,AE=6,请直接写出线段 QN扫过的面积.
1.由图2知,
∵AB=BC,
∵AB=BC, BD⊥AC,
∴AC=2AD, ∠ADB=90°,
在Rt△ABD中,
设点M到AC的距离为h,
∵动点M从A点出发,沿折线AB→BC方向运动,
∴当点M运动到点B时, △ADM的面积最大, 即h=BD,由图2知,△ADM的面积最大为3,
∴AD·BD =6②,
①+2×②得,
∴AD+BD=5(负值舍去),
∴BD=5﹣AD③,
将③代入②得, AD(5–AD)=6,
∴AD=3或AD=2,
∵AD> BD,
∴AD=3,
∴AC=2AD=6,
故选: B.
2.∵PM∥CN,
∴∠PMN=∠MNC,
∵∠MNC=∠PNM,
∴∠PMN=∠PNM,
∴PM=PN,
∵NC=NP,
∴PM=CN,
∵MP∥CN,
∴四边形CNPM是平行四边形,
∵CN=NP,
∴四边形CNPM是菱形,
故①正确;
如图1, 当点P与A重合时, 设BN =x, 则AN=NC=8-x,
在Rt△ABN中,
即
解得x =3,
∴CN=8-3=5,
∵AB=4, BC=8,
故②不正确;
由题知, 当MN过点D时, CN最短, 如图2, 四边形CMPN的面积最小,
此时 菱形
当P点与A点重合时,CN最长,如图1,四边形CMPN的面积最大,
此时
正确,
故选: C.
3.当点P在线段AB上运动时, 是正比例函数,排除B选项;当点P在线段BC上运动时, 当点P在线段CD上运动时, ) ,是一次函数的图象,排除A,C选项,D选项符合题意;故选: D.
4.如图所示,过点B、D分别作 的平行线,交AD、BC于点E、F.
由图象和题意可得.
,
则
∴矩形ABCD的面积为
故答案为:8.
5.如图1中,过点B作 于H.
在 中,
在 中,
当 时, 点. 到直线AB的距离最大,设CA'交AB的延长线于K.
在 中,
如图2中,点P到达点B时,线段 扫过的面积
故答案为:
6.(1)证明: 如图1中,
(2)如图2中, 延长PM交AF于T.
中小学教育资源及组卷应用平台
∴四边形MNFT是平行四边形,
∴当EC的值最大时,PM的值最大,
∵当点E与B重合时,EC的值最大,EC的最大值为 此时
7.(1) 如图①, 连接AF, AC,
∵四边形ABCD和四边形AEFG都是正方形,
理由如下:如图②,连接ME,过点C作( 交直线ME于H, 连接BH, 设CF与AD交点为P, CF与AG交点为R,
∵CH∥EF,
∴∠FCH=∠CFE,
∵点M是CF的中点,
∴CM=MF,
又∵∠CMH=∠FME,
∴△CMH≌△FME(ASA),
∴CH=EF, ME=HM,
∴AE=CH,
∵CH∥EF,AG∥EF,
∴CH∥AG,
∴∠HCF =∠CRA,
∵AD∥BC,
∴∠BCF=∠APR,
∴∠BCH=∠BCF+∠HCF=∠APR+∠ARC,
∵∠DAG+∠APR+∠ARC =180°,
∠BAE+∠DAG=180°,
∴∠BAE=∠BCH,
又∵BC =AB, CH = AE,
∴△BCH≌△BAE(SAS),
∴BH = BE, ∠CBH =∠ABE,
∴∠HBE=∠CBA=90°,
∵MH = ME, 点N是BE中点,
∴BH=2MN,MN∥BH,
∴BE=2MN, MN⊥BE;
(3)如图③, 取AB中点O, 连接ON, OQ, AF,
∵点N是BE的中点,点Q是BF的中点,点O是AB的中点,
∴点Q在以点O为圆心, 为半径的圆上运动,点N在以点O为圆心,3为半径的圆上运动,
∴线段QN扫过的面积=
同课章节目录
