2025年中考数学复习---线、面的动点最值专项练习(含解析)
文档属性
| 名称 | 2025年中考数学复习---线、面的动点最值专项练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 425.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 06:19:05 | ||
图片预览




文档简介
线、面的动点最值专项练习
数轴上运动的线段
【方法技巧】数形结合,设未知数,看清楚动点的速度和方向,表示出线段的点表示的数(注意比较上节内容:数轴上运动的点),再根据题中的等量关系列方程求解.
【题1】★★★如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是-10,点C在数轴上表示的数是16. 若线段 AB 以6个单位长度/秒的速度向右匀速运动,同时线段CD 以2个单位长度/秒的速度向左匀速运动.
(1)问运动多少秒时BC=8(单位长度);
(2)当运动到 BC=8(单位长度)时,点 B在数轴上表示的数是 ;
(3)P 是线段 AB 上一点,当 B 点运动到线段CD上时,是否存在关系式 若存在,求线段PC 的长;若不存在,请说明理由.
【题2】如图,P是定长线段AB上一点,C、D 两点同时从 P、B 出发分别以1cm/s和2cm/s的速度沿直线AB 向左运动(C在线段AP 上,D 在线段 BP 上).已知C、D 运动到任一时刻时,总有 PD=2AC.
(1)线段 AP 与线段 AB 的数量关系是 ;
(2)若Q 是线段AB上一点,且AQ-BQ=PQ,求证:AP=PQ;
(3)若 C、D 运动5s 后,恰好有 AB,此时 C 点停止运动,D 点在线段 PB 上继续运动,M、N分别是 CD、PD 的中点,问 的值是否发生变化 若变化,请说明理由;若不变,请求出 的值.
匀速运动的点形成全等三角形
【方法技巧】数形结合,设未知数,看清楚动点的速度和方向,表示出三角形的边长;根据题中的等量关系列方程求解.分段讨论是重点.
【题1】★★★如图,△ABC中,∠ACB=90°,AC=6,BC=8.点 P 从A 点出发沿A-C-B路径向终点运动,终点为 B 点;点Q 从 B点出发沿B-C-A路径向终点运动,终点为A点.点P 和Q 分别以1 和3 的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥l于 E,QF⊥l于 F.问:点 P 运动多少时间时,△PEC与△QFC全等 请说明理由.
【题2】★★★如图①,AB =4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点 P 在线段AB上以1cm/s的速度由点 A 向点 B 运动,同时,点Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为t(s).
(1)若点 Q 的运动速度与点 P 的运动速度相等,当t =1 时,△ACP 与△BPQ 是否全等,请说明理由,并判断此时线段 PC 和线段PQ 的位置关系;
(2)如图②,将图①中的“AC⊥AB,BD⊥AB”改为“∠CAB =∠DBA =60°”,其他条件不变.设点 Q 的运动速度为x cm/s,是否存在实数x,使得△ACP 与△BPQ 全等 若存在,求出相应的x、t的值;若不存在,请说明理由.
【题3】★★★★如图,在四边形AB-CD中,AD=BC=8,AB=CD,BD=12,点 E从D 点出发,以每秒1个单位的速度沿 DA 向点A匀速移动,点F 从点 C 出发,以每秒3个单位的速度沿 C→B→C,作匀速移动,点 G 从点B 出发沿 BD 向点 D 匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.
(1)试证明:AD∥BC;
(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次 并分别求出此时的移动时间和G点的移动距离.
【题4】 如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D 为AB的中点.如果点 P 在线段 BC 上以3cm/s的速度由B 点向 C 点运动,同时,点 Q 在线段 CA 上由 C点向A 点运动.
(1)若点 Q 的运动速度与点 P 的运动速度相等,经过1s后,△BPD 与△CQP 是否全等,请说明理由;
(2)若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP全等
若点 Q 以(2)中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,求经过多长时间点 P与点 Q 第一次在△ABC 的哪条边上相遇
四边形中匀速运动的点
【方法技巧】平行四边形中匀速运动的点,可以设运动时间为t,然后用t表示各个变量求解;线段的最值常用两边之和大于第三边或垂线段最短求解.
中小学教育资源及组卷应用平台
【题1】★★★如图,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点 P 从点A 向点 D 以 1cm/s 的速度运动,到点 D 即停止。同时点 Q 从点 C 向点 B 以2cm/s的速度运动,到点 B 即停止.直线 PQ 将四边形 ABCD截成两个四边形,分别为四边形ABQP 和四边形 PQCD,则当P、Q 两点同时出发几秒时所截得两个四边形中,其中一个四边形为平行四边形
【题2】★★★如图,矩形ABCD 中,对角线AC,BD 相交于点 O,点 P 是线段AD 上一动点(不与点 D 重合),PO 的延长线交 BC于点Q.
(1)求证:四边形 PBQD 为平行四边形;
(2)若AB=3cm,AD=4cm,点P从点A出发,以1cm/s的速度向点 D 匀速运动,设点 P运动时间为 ts,问四边形 PBQD 能够成为菱形吗 如果能,求出相应的t值;如果不能,说明理由.
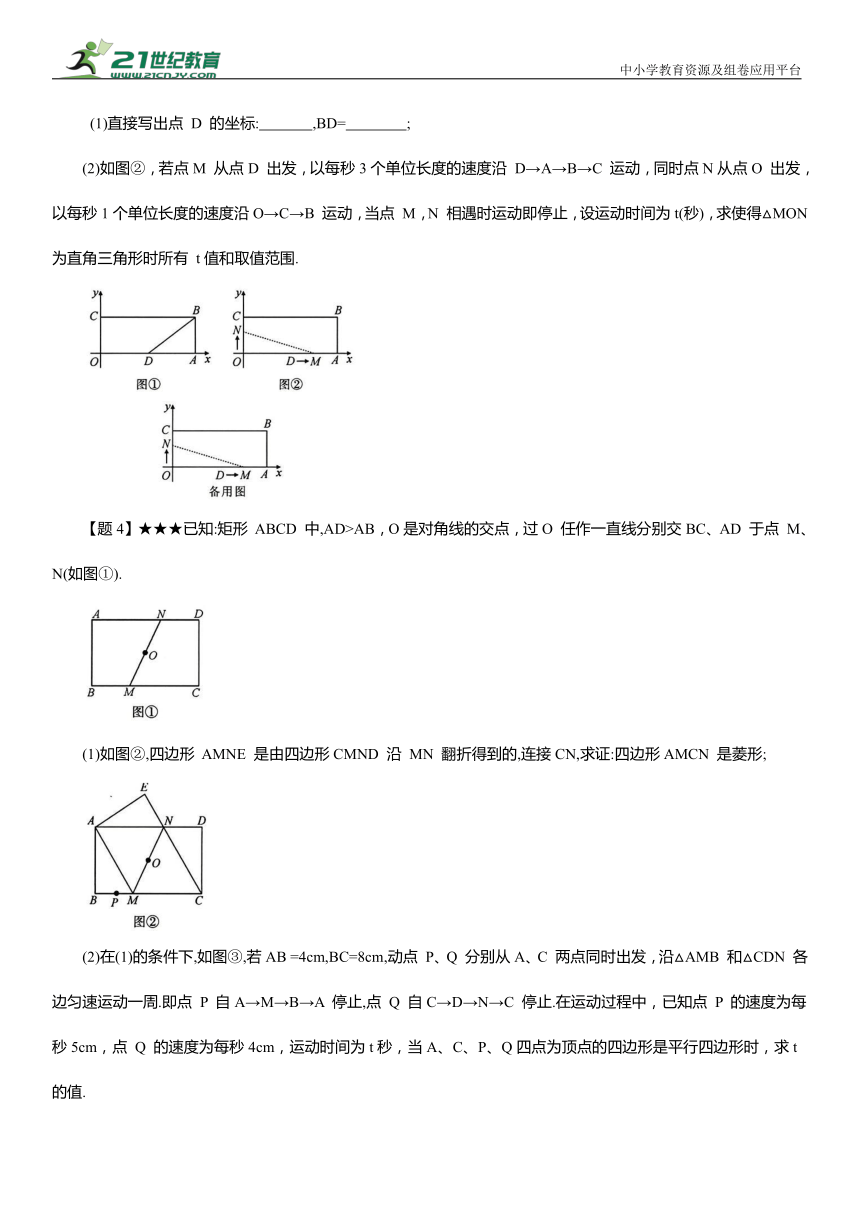
【题3】★★★如图①,在平面直角坐标系中,矩形OABC的顶点A,C的坐标分别为A(12,0),C(0,4),点 D 为 OA 边的中点,连接BD.
(1)直接写出点 D 的坐标: ,BD= ;
(2)如图②,若点M 从点D 出发,以每秒3个单位长度的速度沿 D→A→B→C 运动,同时点N从点O 出发,以每秒1个单位长度的速度沿O→C→B 运动,当点 M,N 相遇时运动即停止,设运动时间为t(秒),求使得△MON 为直角三角形时所有 t值和取值范围.
【题4】★★★已知:矩形 ABCD 中,AD>AB,O是对角线的交点,过O 任作一直线分别交BC、AD 于点 M、N(如图①).
(1)如图②,四边形 AMNE 是由四边形CMND 沿 MN 翻折得到的,连接CN,求证:四边形AMCN 是菱形;
(2)在(1)的条件下,如图③,若AB =4cm,BC=8cm,动点 P、Q 分别从A、C 两点同时出发,沿△AMB 和△CDN 各边匀速运动一周.即点 P 自A→M→B→A 停止,点 Q 自C→D→N→C 停止.在运动过程中,已知点 P 的速度为每秒5cm,点 Q 的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
【题5】★★★★如图,在平面直角坐标系中,AB∥OC,A(0,12),B(a,c),C(b,0),并且a,b满足 动点 P 从点A 出发.在线段AB 上以每秒2个单位长度的速度向点 B 运动;动点 Q 从点 O 出发,在线段OC 上以每秒1个单位长度的速度向点 C运动,点P,Q分别从点A,O同时出发,当点 P 运动到点B 时,点Q 随之停止运动.设运动时间为t(秒).
(1)求B,C两点的坐标;
(2)当t为何值时,四边形 PQCB 是平行四边形 并求出此时P,Q两点的坐标;
(3)当t为何值时,△PQC 是以 PQ 为腰的等腰三角形 并求出 P,Q两点的坐标.
动态路径问题
【方法技巧】动点的运动路径问题解题方法:
(1)选取多个特殊点探索多个特殊位置,一般选取起点,终点,和另外的特殊点探索.
(2)根据这些特殊点的位置猜想运动路径,然后验证.现阶段多用全等转换求值.
(3)设点的坐标→证全等→根据题目条件列式求解.
题1】★★如图,A(1,0),B(0,1),点 P 在线段 OA 上运动,BP⊥PM,BP =PM,C为x轴负半轴上一定点,连接CM,N 为 CM 的中点,当点 P 从点 O 运动至点A 时,点N 运动的路径长为 .
【题2】★★★如图,在平面直角坐标系中,正方形ABCO 的顶点 C,A 分别在x,y轴上,A(0,6),点Q 为对角线 BO上一动点,D 为边OA上一点,DQ⊥CQ,点 Q 从点 B 出发,沿BO方向移动,若移动的路径长为3,直接写出CD 的中点 M 移动的路径长为 .
2.【思路分析】点 Q 和点 B 重合时,D 在A点才符合题意,连AC 交 BO 于点N,这时M点即为N点.即M 移动的路径长为 MN.
【题3】★★如图,直线AB:y=2x+4交x轴于点A,交y轴于点 B,C(1,0),P为直线AB上一点,将线段 PC 绕点 C 顺时针旋转90°得CQ.
(1)当P 从点A 运动到点 B 时,点 Q 的运动路径长为 ;
(2)线段OQ 的最小值为 .
【题4】★★★如图,A(4,0),B(0,4),点 P 在线段 AB 上运动,PQ⊥PO 且 PQ=PO.
(1)试说明点 Q 在某一确定的直线上;
(2)点M 是OQ 的中点,当点 P 从点 A 运动到点 B 时,求点 M 运动的路径长.
【思路分析】(1)yAB = - x +4,设 P(a,-a+4),过点P作EF∥x轴交y轴于点E,过点 Q 作 QF ⊥ PE 于点 F,可证△POE ≌△QPF,则 FQ = PE = a,PF = OE = - a +4.∴Q(4,4-2a),则点Q在直线x=4上;
(2)由M为OQ 中点得xM=2,当点 P 与起点A 重合时,M (2,-2),当点P 与终点B重合时,M (2,2),故点M的路径长为
【题5】★★★如图,在△ABC中,∠B=90°,∠BAC=60°,AB=1,若点 E 为 BC 上一动点,以AE 为边在 AE 右侧作等边△AEF,连接 CF,点 G 为线段 CF的中点,若点 E 从点 B出发,沿着 BC 方向运动到点 C,则在此过程中,点G运动的路径长为 .
【题6】在平面直角坐标系中,点A(0,8)、C(8,0),四边形AOCB 是正方形,点 D 是x轴正半轴上的一动点,∠ADE =90°,DE交正方形 AOCB 的外角的平分线 CE于点 E.
(1)当点 D 是 OC 的中点时,求证 AD=DE;
(2)连接AE,点 F 是 AE 的中点,当点 D在x轴正半轴上运动时,点F 到 CE 的距离是否为定值 若为定值,求出这个值;若不是定值,请说明理由.
1.【答案解析】
(1)点 B 在数轴上表示的数是-10+2 =-8,点 D 在数轴上表示的数是16+4 =20,运动t时后:A 表示的数为-10 +6t,B 表示的数为-8+6t,C表示的数为16-2t,D 表示的数为20-2t.
由 BC=8得到|-8+6t-16+2t|=8 t=4或t=2.故运动2秒或4秒后,BC=8.
(2)当运动2秒时,点B 在数轴上表示的数是4;
当运动4 秒时,点B 在数轴上表示的数是16.
(3)存在关系式
设运动时间为t秒,设P 原来表示的数为x,运动t时后:A表示的数为6t-10,B 表示的数为6t-8,C 表示的数为16-2t,D 表示的数为20-2t,P 表示的数为x+6t,BD=28-8t,
AP=x+10,PC=|8t+x-16|.
代入 解得x =15-8t或者x
所以.PC=|8t+x-16|=1或
2.【答案解析】
(1)根据C、D的运动速度知:BD=2PC,
∵PD=2AC,∴BD+PD=2(PC+AC),即PB=2AP,
∴点P 在线段AB上的 处,即AB=3AP.
(2)证明:如下图,由题意得AQ>BQ,
∴AQ=AP+PQ,
又∵AQ-BQ=PQ,∴AQ=BQ+PQ,
∴AP=BQ.
由(1)得,
∴ PQ =AB - AP - BQ =AB - 2AP =AB -
∴AP=PQ.
(3)如下图:
运动5s时,PC =5cm,BD =10cm. 由(1)可知
设AP=x,则AC=AP-PC=x-5,
∴PD=2AC=2x-10,PB=PD+DB=2x,CD=2x-5,AB=AP+PB=3x.
则D 仍为动点,设A为原点,∵AB =3AP=30 ∴B 表示的数为30,设运动了t 秒(t>5)则D表示的数为30-2t,
∵C表示的数是10-5 =5,M为CD 的中点,∴M 表示的数为
∵ N 为 PD 的中点,∴ N 表示的数为
为定值.
1.【思路分析】数形结合,设未知数,看清楚动点的速度和方向,表示出△PEC 和△QFC的边长.
根据题中的等量关系列方程求解.需分段讨论.
【答案解析】
解:设运动时间为t,分三种情况:①0∵ ∠ACB =90°,∴ ∠ACE +∠QCF =90°,∴ ∠QCF=∠CPE,∴△PCE∽△CQF.
此时要得△PCE≌△CQF,则 PC =CQ 即6-t=8-3t,t=1,满足.
时,P,Q 都在AC 上,此时两个三角形如果全等,则它们必须是重合的,
PC=CQ 即 满足.
时,Q已经在A 点停止运动,此时P不可能在AC上,即t>6,和①一样的原因可知,此时PC=CQ 即满足PC=AC=6,
∴t=6+6=12,
综上t=1 或 或t=12.
2.【思路分析】(2)设未知数,表示出△ACP和BPQ的边长,根据题中的等量关系列方程求解.需分“AC =BP,AP = BQ”和“AC = BQ,AP=BP”两种情况进行讨论.
【答案解析】解:(1)当t =1 时,AP = BQ=1,BP=AC=3,
∵∠A=∠B=90°,∴ △ACP≌△BPQ.
此时∠ACP =∠BPQ,∠APC + ∠BPQ =∠APC+∠ACP=90°,
∴∠CPQ=90°,即线段 PC⊥线段 PQ.
(2)①若△ACP≌△BPQ,则AC=BP,AP=BQ,
有 解得
②若△ACP≌△BQP,则 AC = BQ,AP=BP,
有 解得
综上,存在 或 使得△ACP 与△BPQ 全等.
3.【答案解析】(1) 证明:在 △ABD 和△CDB中,
∵AD=BC,AB=CD,BD=DB,
∴△ABD≌△CDB,
∴∠CBD=∠ADB,∴AD∥BC.
(2)设G点的移动距离为y,当F由 C→B移动,即
∵△DEG≌△BFG,∴∠EDG=∠FBG,
∴DE=BF,DG=BG或
DE=BG,DG=BF,即
解得 或
解得 (舍去).
当F由B→C移动,即
有 解得
或 解得
综上所述,这种情况会出现3次.
4.【分析】由(2)可得出点Q 的速度大于点 P 的速度,点Q 追上点 P,要比点 P 多运动AC+AB的距离.点Q 的路程-点P 的路程=10cm×2.
【答案解析】(1)①∵t= ls,∴ BP =CQ =3×1=3cm,∵AB=10cm,点 D 为AB 的中点,∴BD=5cm.又∵PC=BC-BP,BC =8cm,∴PC=8-3=5cm,∴ PC =BD.又∵AB =AC,∴∠B=∠C,∴△BPD≌△CQP.
②∵vp≠vρ,∴BP≠CQ,又∵ △BPD≌△CQP,∠B=∠C,则BP=PC=4,CQ=BD =5,∴点 P、点 Q 运动的时间
(2)设经过x秒后点 P 与点 Q 第一次相遇,由题意,得
解得
∴点 P 共运动了
∵80=2×28+24,∴ 点 P、点 Q 在 AB 边上相遇,
∴经过8 ,点P与点Q第一次在边AB上相遇.
1.【思路分析】设未知数,看清楚动点的速度和方向,表示线段长度;根据题中的等量关系列方程;其中要注意因为动点引起的分类讨论,这是许多同学容易遗漏的,也是这类题目的难点.
本题分两种情况,当四边形ABQP 为平行四边形时,AP=BQ;当四边形PQCD 为平行四边形时,PD=QC.
【答案解析】解:设当 P、Q两点同时出发t(s)时,四边形 ABQP 或四边形 PQCD 是平行四边形,根据题意,得AP = tcm,PD=(24-t) cm,CQ=2tcm,BQ=(30-2t) cm(0①若四边形ABQP 是平行四边形,
∵AD∥BC,∴还需满足AP =BQ,∴t=30-2t,解得t=10,
∴10s时四边形ABQP 是平行四边形;
②若四边形 PQCD 是平行四边形,
∵AD∥BC,∴还需满足 PD=CQ,
∴24-t=2t,解得t=8,∴8s时四边形PQCD 是平行四边形.
综上所述,当P、Q 两点同时出发8s或10s时,截得两个四边形中,其中一个四边形为平行四边形.
2.【思路分析】(1)证△POD≌△QOB.
(2)当 PB = PD 时,□PBQD 为菱形,设AP=t,则 PD= PB=(4-t),由勾股定理列方程求解.
【答案解析】(1)证明:∵四边形ABCD 是矩形,∴AD∥BC,OD= OB,∠PDO=∠QBO,
在△POD 和△QOB 中,∠PDO =∠QBO,OD= OB,∠POD=∠QOB,
∴△POD≌△QOB(ASA),∴ PD =QB ,又∵PD∥QB,
∴ 四边形 PBQD 为平行四边形.
(2)点P 从点A出发运动1s时,AP = tcm,PD=(4-t) cm.
当四边形 PBQD 是菱形时,PB =PD =(4-t) cm.
∵四边形ABCD 是矩形,∴ ∠BAP=90°.
在 Rt△ABP 中, PB ,即.
解得 ∴点P 运动时间为 时,四边形 PBQD 为菱形.
3.【答案解析】(1)(6,0),2
(2)①如图①所示:
∵OC=4,DA=6,
∴点N从O到C 需要4s,点 M 从 D 到A需要2s.
∴0∴当0②如图②所示:
当MN⊥OC时,△MON是直角三角形.
∵MN⊥OC,∴∠MNO=90°.
∴ ∠MNO =∠NOA =∠OAM.
∴四边形OAMN为矩形.
∴ON=AM.∴t=3t-6.
解得:t=3.
∴当t=3s时,△NOM为直角三角形.
③如图③所示:
当点 N 与点 C 重合时,△NOM 为直角三角形.
∵ON=OC=4,3t=4
综上所述,当04.【答案解析】(1)证法一:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵BM=DN(△BOM≌△DCN),
∴AD-DN=BC-BM,
即AN=CM,
∴ 四边形AMCN 是平行四边形,
由翻折得,AM=CM,
∴四边形AMCN 是菱形;
证法二:由翻折得,AN = NC,AM = MC,∠AMN=∠CMN,
∵AD∥BC,
∴ ∠ANM=∠CMN,
∴∠AMN=∠ANM,
∴AM=AN,
∴AM=MC=CN=NA,
∴ 四边形AMCN 是菱形;
(2)设菱形 AMCN 的边长为 x cm,则 BM=8-x,
在Rt△ABM中,
即
解得x=5,∴AM=5cm,
显然,当点 P 在AM 上时,点 Q 在 CD 上,此时A、C、P、Q四点不可能构成平行四边形,同理,点 P 在 AB 上时,点 Q 在 DN 或 CN 上,此时A、C、P、Q四点也不可能构成平行四边形,因此,只有点 P 在 BM 上,点 Q 在 DN 上时,才能构成平行四边形,此时PC=QA.
∵点 P 的速度为每秒5cm,点 Q 的速度为每秒4cm,运动时间为t,
∴ PC=PM+MC=PM+AM=5t,
QA=AD+CD-CQ=8+4-4t=12-4t,
∴5t=12-4t,解得
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,
5.【思路分析】(2) PB = QC 时,四边形PQCB为平行四边形;
(3)设未知数,建立方程求解.需分 PQ =CQ 和PQ=PC 两种情况讨论.
【答案解析】解: 1--a+16,∴a=21,b=16.
∵AB∥OC,A(0,12),∴c=12,∴ B(21,12),C(16,0);
(2)由题意,得AP =2t,QO=t,则 PB =21-2t,QC=16-t,
∵当PB=QC时,四边形 PQCB 是平行四边形,∴21--2t=16-t,解得t=5,∴ P(10,12),Q(5,0);
(3)当PQ=CQ时,如下图,过Q 作QN⊥AB于点N,
由题意,得PN=t,则 解得t=3.5,
∴P(7,12),Q(3.5,0).
当PQ=PC时,过P作PM⊥x轴于点M,
由题意,得QM=t,CM =16-2t,则t= 16-2t,解得
综上所述:P (7,12),Q (3.5,0);P ( 12),
1.【思路分析】点P 在OA 上运动,分别标出点P 在点O 和 P 在点 A 时 M 的位置.当点 P在点O 时,N在CA的中点位置,当点 P 在点A时,N在CM的中点位置,即N 运动的路径长
【答案解析】设 CA的中点为 E,连接EN.当点 P 在点 O 时,点N位置时点 E 的位置,当点 P 在点A时,N在如下图位置,点N 运动的路径长为 EN 的长度.
∵BP⊥PM,BP=PM,∴BA⊥AM,且BA =
2.【答案解析】作 QH⊥OA 于点 H,QG⊥OC于点G,
则易证△QHD≌△QGC(AAS)(证明过程略),
∴QD =QC = QA,∴ AH = DH= BQ=
连接 CA 交 BO 于点 N,则点 N 为 CA 的中点,MN为△ACD的中位线,
∵M为CD的中点,D 在 OA 上运动,M在中位线MN上运动,
∴运动的路径长为
3.【思路分析】作垂直于坐标轴的垂线,设点的坐标→证全等→根据题目条件列式求解.
过点 P作PE⊥x轴于点 E,过点 Q 作QF⊥x轴于点F,
设P(t,2t+4),可证△PCE≌△CQF),
∴QF=EC=1-t,CF =PE=2t+4,OF =2t+5,则Q(2t+5,1-t).
解:(1)点P 从点A到点B路径与点 Q 运动路径长相等,为
(2)令x=2t+5,y=1-t,则 当OQ⊥直线 时最小,由面积法求出 OQ 的最小值为
5【思路分析】G点在 CF 上,C 是定点,F是动点.因此分别标出当 E在点B 处时和点E在点 C 时 F 点的位置,就可得到G点路径.
【答案解析】当E在点B处时,点F在AC边上,为AC中点.
设为点 M,取 MC 中点 N,此时点 G 的起点为点 N.
当点 E 运动到点 C 时,点F 以 AC 为边的等边△ACH 的顶点 H,
此时G为CH的中点 R,
即点G运动的路径长为32
6.【答案解析】解:(1)如图:取 OA 的中点M,连接MD.
∵OA =OC,∴OM =OD,∴ ∠OMD =45°=∠ECB,∴∠AMD=135°=∠DCE,
又∵ ∠MAD + ∠ADO = 90°,∠CDE +∠ADO=90°,∴∠MAD=∠CDE,
在△AMD 和△DCE中
∴△AMD≌△DCE,∴AD=DE.
(2)连接FC、AC,作 BP⊥AD交y轴于 P.
∵∠ACB=45°,∠BCE=45°,
∴∠ACE=90°,
∵F为AE中点,∴AF=EF=FC,
∵点 F在AC 的垂直平分线上,
∵OB 垂直平分AC,∴点F在直线OB上,AC⊥CE,AC⊥OB,∴OB∥CE,
∴ 点 F 到直线 CE 的距离为定值且等于 AC,点F到CE的距离
数轴上运动的线段
【方法技巧】数形结合,设未知数,看清楚动点的速度和方向,表示出线段的点表示的数(注意比较上节内容:数轴上运动的点),再根据题中的等量关系列方程求解.
【题1】★★★如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是-10,点C在数轴上表示的数是16. 若线段 AB 以6个单位长度/秒的速度向右匀速运动,同时线段CD 以2个单位长度/秒的速度向左匀速运动.
(1)问运动多少秒时BC=8(单位长度);
(2)当运动到 BC=8(单位长度)时,点 B在数轴上表示的数是 ;
(3)P 是线段 AB 上一点,当 B 点运动到线段CD上时,是否存在关系式 若存在,求线段PC 的长;若不存在,请说明理由.
【题2】如图,P是定长线段AB上一点,C、D 两点同时从 P、B 出发分别以1cm/s和2cm/s的速度沿直线AB 向左运动(C在线段AP 上,D 在线段 BP 上).已知C、D 运动到任一时刻时,总有 PD=2AC.
(1)线段 AP 与线段 AB 的数量关系是 ;
(2)若Q 是线段AB上一点,且AQ-BQ=PQ,求证:AP=PQ;
(3)若 C、D 运动5s 后,恰好有 AB,此时 C 点停止运动,D 点在线段 PB 上继续运动,M、N分别是 CD、PD 的中点,问 的值是否发生变化 若变化,请说明理由;若不变,请求出 的值.
匀速运动的点形成全等三角形
【方法技巧】数形结合,设未知数,看清楚动点的速度和方向,表示出三角形的边长;根据题中的等量关系列方程求解.分段讨论是重点.
【题1】★★★如图,△ABC中,∠ACB=90°,AC=6,BC=8.点 P 从A 点出发沿A-C-B路径向终点运动,终点为 B 点;点Q 从 B点出发沿B-C-A路径向终点运动,终点为A点.点P 和Q 分别以1 和3 的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥l于 E,QF⊥l于 F.问:点 P 运动多少时间时,△PEC与△QFC全等 请说明理由.
【题2】★★★如图①,AB =4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点 P 在线段AB上以1cm/s的速度由点 A 向点 B 运动,同时,点Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为t(s).
(1)若点 Q 的运动速度与点 P 的运动速度相等,当t =1 时,△ACP 与△BPQ 是否全等,请说明理由,并判断此时线段 PC 和线段PQ 的位置关系;
(2)如图②,将图①中的“AC⊥AB,BD⊥AB”改为“∠CAB =∠DBA =60°”,其他条件不变.设点 Q 的运动速度为x cm/s,是否存在实数x,使得△ACP 与△BPQ 全等 若存在,求出相应的x、t的值;若不存在,请说明理由.
【题3】★★★★如图,在四边形AB-CD中,AD=BC=8,AB=CD,BD=12,点 E从D 点出发,以每秒1个单位的速度沿 DA 向点A匀速移动,点F 从点 C 出发,以每秒3个单位的速度沿 C→B→C,作匀速移动,点 G 从点B 出发沿 BD 向点 D 匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.
(1)试证明:AD∥BC;
(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次 并分别求出此时的移动时间和G点的移动距离.
【题4】 如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D 为AB的中点.如果点 P 在线段 BC 上以3cm/s的速度由B 点向 C 点运动,同时,点 Q 在线段 CA 上由 C点向A 点运动.
(1)若点 Q 的运动速度与点 P 的运动速度相等,经过1s后,△BPD 与△CQP 是否全等,请说明理由;
(2)若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP全等
若点 Q 以(2)中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,求经过多长时间点 P与点 Q 第一次在△ABC 的哪条边上相遇
四边形中匀速运动的点
【方法技巧】平行四边形中匀速运动的点,可以设运动时间为t,然后用t表示各个变量求解;线段的最值常用两边之和大于第三边或垂线段最短求解.
中小学教育资源及组卷应用平台
【题1】★★★如图,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点 P 从点A 向点 D 以 1cm/s 的速度运动,到点 D 即停止。同时点 Q 从点 C 向点 B 以2cm/s的速度运动,到点 B 即停止.直线 PQ 将四边形 ABCD截成两个四边形,分别为四边形ABQP 和四边形 PQCD,则当P、Q 两点同时出发几秒时所截得两个四边形中,其中一个四边形为平行四边形
【题2】★★★如图,矩形ABCD 中,对角线AC,BD 相交于点 O,点 P 是线段AD 上一动点(不与点 D 重合),PO 的延长线交 BC于点Q.
(1)求证:四边形 PBQD 为平行四边形;
(2)若AB=3cm,AD=4cm,点P从点A出发,以1cm/s的速度向点 D 匀速运动,设点 P运动时间为 ts,问四边形 PBQD 能够成为菱形吗 如果能,求出相应的t值;如果不能,说明理由.
【题3】★★★如图①,在平面直角坐标系中,矩形OABC的顶点A,C的坐标分别为A(12,0),C(0,4),点 D 为 OA 边的中点,连接BD.
(1)直接写出点 D 的坐标: ,BD= ;
(2)如图②,若点M 从点D 出发,以每秒3个单位长度的速度沿 D→A→B→C 运动,同时点N从点O 出发,以每秒1个单位长度的速度沿O→C→B 运动,当点 M,N 相遇时运动即停止,设运动时间为t(秒),求使得△MON 为直角三角形时所有 t值和取值范围.
【题4】★★★已知:矩形 ABCD 中,AD>AB,O是对角线的交点,过O 任作一直线分别交BC、AD 于点 M、N(如图①).
(1)如图②,四边形 AMNE 是由四边形CMND 沿 MN 翻折得到的,连接CN,求证:四边形AMCN 是菱形;
(2)在(1)的条件下,如图③,若AB =4cm,BC=8cm,动点 P、Q 分别从A、C 两点同时出发,沿△AMB 和△CDN 各边匀速运动一周.即点 P 自A→M→B→A 停止,点 Q 自C→D→N→C 停止.在运动过程中,已知点 P 的速度为每秒5cm,点 Q 的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
【题5】★★★★如图,在平面直角坐标系中,AB∥OC,A(0,12),B(a,c),C(b,0),并且a,b满足 动点 P 从点A 出发.在线段AB 上以每秒2个单位长度的速度向点 B 运动;动点 Q 从点 O 出发,在线段OC 上以每秒1个单位长度的速度向点 C运动,点P,Q分别从点A,O同时出发,当点 P 运动到点B 时,点Q 随之停止运动.设运动时间为t(秒).
(1)求B,C两点的坐标;
(2)当t为何值时,四边形 PQCB 是平行四边形 并求出此时P,Q两点的坐标;
(3)当t为何值时,△PQC 是以 PQ 为腰的等腰三角形 并求出 P,Q两点的坐标.
动态路径问题
【方法技巧】动点的运动路径问题解题方法:
(1)选取多个特殊点探索多个特殊位置,一般选取起点,终点,和另外的特殊点探索.
(2)根据这些特殊点的位置猜想运动路径,然后验证.现阶段多用全等转换求值.
(3)设点的坐标→证全等→根据题目条件列式求解.
题1】★★如图,A(1,0),B(0,1),点 P 在线段 OA 上运动,BP⊥PM,BP =PM,C为x轴负半轴上一定点,连接CM,N 为 CM 的中点,当点 P 从点 O 运动至点A 时,点N 运动的路径长为 .
【题2】★★★如图,在平面直角坐标系中,正方形ABCO 的顶点 C,A 分别在x,y轴上,A(0,6),点Q 为对角线 BO上一动点,D 为边OA上一点,DQ⊥CQ,点 Q 从点 B 出发,沿BO方向移动,若移动的路径长为3,直接写出CD 的中点 M 移动的路径长为 .
2.【思路分析】点 Q 和点 B 重合时,D 在A点才符合题意,连AC 交 BO 于点N,这时M点即为N点.即M 移动的路径长为 MN.
【题3】★★如图,直线AB:y=2x+4交x轴于点A,交y轴于点 B,C(1,0),P为直线AB上一点,将线段 PC 绕点 C 顺时针旋转90°得CQ.
(1)当P 从点A 运动到点 B 时,点 Q 的运动路径长为 ;
(2)线段OQ 的最小值为 .
【题4】★★★如图,A(4,0),B(0,4),点 P 在线段 AB 上运动,PQ⊥PO 且 PQ=PO.
(1)试说明点 Q 在某一确定的直线上;
(2)点M 是OQ 的中点,当点 P 从点 A 运动到点 B 时,求点 M 运动的路径长.
【思路分析】(1)yAB = - x +4,设 P(a,-a+4),过点P作EF∥x轴交y轴于点E,过点 Q 作 QF ⊥ PE 于点 F,可证△POE ≌△QPF,则 FQ = PE = a,PF = OE = - a +4.∴Q(4,4-2a),则点Q在直线x=4上;
(2)由M为OQ 中点得xM=2,当点 P 与起点A 重合时,M (2,-2),当点P 与终点B重合时,M (2,2),故点M的路径长为
【题5】★★★如图,在△ABC中,∠B=90°,∠BAC=60°,AB=1,若点 E 为 BC 上一动点,以AE 为边在 AE 右侧作等边△AEF,连接 CF,点 G 为线段 CF的中点,若点 E 从点 B出发,沿着 BC 方向运动到点 C,则在此过程中,点G运动的路径长为 .
【题6】在平面直角坐标系中,点A(0,8)、C(8,0),四边形AOCB 是正方形,点 D 是x轴正半轴上的一动点,∠ADE =90°,DE交正方形 AOCB 的外角的平分线 CE于点 E.
(1)当点 D 是 OC 的中点时,求证 AD=DE;
(2)连接AE,点 F 是 AE 的中点,当点 D在x轴正半轴上运动时,点F 到 CE 的距离是否为定值 若为定值,求出这个值;若不是定值,请说明理由.
1.【答案解析】
(1)点 B 在数轴上表示的数是-10+2 =-8,点 D 在数轴上表示的数是16+4 =20,运动t时后:A 表示的数为-10 +6t,B 表示的数为-8+6t,C表示的数为16-2t,D 表示的数为20-2t.
由 BC=8得到|-8+6t-16+2t|=8 t=4或t=2.故运动2秒或4秒后,BC=8.
(2)当运动2秒时,点B 在数轴上表示的数是4;
当运动4 秒时,点B 在数轴上表示的数是16.
(3)存在关系式
设运动时间为t秒,设P 原来表示的数为x,运动t时后:A表示的数为6t-10,B 表示的数为6t-8,C 表示的数为16-2t,D 表示的数为20-2t,P 表示的数为x+6t,BD=28-8t,
AP=x+10,PC=|8t+x-16|.
代入 解得x =15-8t或者x
所以.PC=|8t+x-16|=1或
2.【答案解析】
(1)根据C、D的运动速度知:BD=2PC,
∵PD=2AC,∴BD+PD=2(PC+AC),即PB=2AP,
∴点P 在线段AB上的 处,即AB=3AP.
(2)证明:如下图,由题意得AQ>BQ,
∴AQ=AP+PQ,
又∵AQ-BQ=PQ,∴AQ=BQ+PQ,
∴AP=BQ.
由(1)得,
∴ PQ =AB - AP - BQ =AB - 2AP =AB -
∴AP=PQ.
(3)如下图:
运动5s时,PC =5cm,BD =10cm. 由(1)可知
设AP=x,则AC=AP-PC=x-5,
∴PD=2AC=2x-10,PB=PD+DB=2x,CD=2x-5,AB=AP+PB=3x.
则D 仍为动点,设A为原点,∵AB =3AP=30 ∴B 表示的数为30,设运动了t 秒(t>5)则D表示的数为30-2t,
∵C表示的数是10-5 =5,M为CD 的中点,∴M 表示的数为
∵ N 为 PD 的中点,∴ N 表示的数为
为定值.
1.【思路分析】数形结合,设未知数,看清楚动点的速度和方向,表示出△PEC 和△QFC的边长.
根据题中的等量关系列方程求解.需分段讨论.
【答案解析】
解:设运动时间为t,分三种情况:①0
此时要得△PCE≌△CQF,则 PC =CQ 即6-t=8-3t,t=1,满足.
时,P,Q 都在AC 上,此时两个三角形如果全等,则它们必须是重合的,
PC=CQ 即 满足.
时,Q已经在A 点停止运动,此时P不可能在AC上,即t>6,和①一样的原因可知,此时PC=CQ 即满足PC=AC=6,
∴t=6+6=12,
综上t=1 或 或t=12.
2.【思路分析】(2)设未知数,表示出△ACP和BPQ的边长,根据题中的等量关系列方程求解.需分“AC =BP,AP = BQ”和“AC = BQ,AP=BP”两种情况进行讨论.
【答案解析】解:(1)当t =1 时,AP = BQ=1,BP=AC=3,
∵∠A=∠B=90°,∴ △ACP≌△BPQ.
此时∠ACP =∠BPQ,∠APC + ∠BPQ =∠APC+∠ACP=90°,
∴∠CPQ=90°,即线段 PC⊥线段 PQ.
(2)①若△ACP≌△BPQ,则AC=BP,AP=BQ,
有 解得
②若△ACP≌△BQP,则 AC = BQ,AP=BP,
有 解得
综上,存在 或 使得△ACP 与△BPQ 全等.
3.【答案解析】(1) 证明:在 △ABD 和△CDB中,
∵AD=BC,AB=CD,BD=DB,
∴△ABD≌△CDB,
∴∠CBD=∠ADB,∴AD∥BC.
(2)设G点的移动距离为y,当F由 C→B移动,即
∵△DEG≌△BFG,∴∠EDG=∠FBG,
∴DE=BF,DG=BG或
DE=BG,DG=BF,即
解得 或
解得 (舍去).
当F由B→C移动,即
有 解得
或 解得
综上所述,这种情况会出现3次.
4.【分析】由(2)可得出点Q 的速度大于点 P 的速度,点Q 追上点 P,要比点 P 多运动AC+AB的距离.点Q 的路程-点P 的路程=10cm×2.
【答案解析】(1)①∵t= ls,∴ BP =CQ =3×1=3cm,∵AB=10cm,点 D 为AB 的中点,∴BD=5cm.又∵PC=BC-BP,BC =8cm,∴PC=8-3=5cm,∴ PC =BD.又∵AB =AC,∴∠B=∠C,∴△BPD≌△CQP.
②∵vp≠vρ,∴BP≠CQ,又∵ △BPD≌△CQP,∠B=∠C,则BP=PC=4,CQ=BD =5,∴点 P、点 Q 运动的时间
(2)设经过x秒后点 P 与点 Q 第一次相遇,由题意,得
解得
∴点 P 共运动了
∵80=2×28+24,∴ 点 P、点 Q 在 AB 边上相遇,
∴经过8 ,点P与点Q第一次在边AB上相遇.
1.【思路分析】设未知数,看清楚动点的速度和方向,表示线段长度;根据题中的等量关系列方程;其中要注意因为动点引起的分类讨论,这是许多同学容易遗漏的,也是这类题目的难点.
本题分两种情况,当四边形ABQP 为平行四边形时,AP=BQ;当四边形PQCD 为平行四边形时,PD=QC.
【答案解析】解:设当 P、Q两点同时出发t(s)时,四边形 ABQP 或四边形 PQCD 是平行四边形,根据题意,得AP = tcm,PD=(24-t) cm,CQ=2tcm,BQ=(30-2t) cm(0
∵AD∥BC,∴还需满足AP =BQ,∴t=30-2t,解得t=10,
∴10s时四边形ABQP 是平行四边形;
②若四边形 PQCD 是平行四边形,
∵AD∥BC,∴还需满足 PD=CQ,
∴24-t=2t,解得t=8,∴8s时四边形PQCD 是平行四边形.
综上所述,当P、Q 两点同时出发8s或10s时,截得两个四边形中,其中一个四边形为平行四边形.
2.【思路分析】(1)证△POD≌△QOB.
(2)当 PB = PD 时,□PBQD 为菱形,设AP=t,则 PD= PB=(4-t),由勾股定理列方程求解.
【答案解析】(1)证明:∵四边形ABCD 是矩形,∴AD∥BC,OD= OB,∠PDO=∠QBO,
在△POD 和△QOB 中,∠PDO =∠QBO,OD= OB,∠POD=∠QOB,
∴△POD≌△QOB(ASA),∴ PD =QB ,又∵PD∥QB,
∴ 四边形 PBQD 为平行四边形.
(2)点P 从点A出发运动1s时,AP = tcm,PD=(4-t) cm.
当四边形 PBQD 是菱形时,PB =PD =(4-t) cm.
∵四边形ABCD 是矩形,∴ ∠BAP=90°.
在 Rt△ABP 中, PB ,即.
解得 ∴点P 运动时间为 时,四边形 PBQD 为菱形.
3.【答案解析】(1)(6,0),2
(2)①如图①所示:
∵OC=4,DA=6,
∴点N从O到C 需要4s,点 M 从 D 到A需要2s.
∴0
当MN⊥OC时,△MON是直角三角形.
∵MN⊥OC,∴∠MNO=90°.
∴ ∠MNO =∠NOA =∠OAM.
∴四边形OAMN为矩形.
∴ON=AM.∴t=3t-6.
解得:t=3.
∴当t=3s时,△NOM为直角三角形.
③如图③所示:
当点 N 与点 C 重合时,△NOM 为直角三角形.
∵ON=OC=4,3t=4
综上所述,当0
∴AD∥BC,AD=BC,
∵BM=DN(△BOM≌△DCN),
∴AD-DN=BC-BM,
即AN=CM,
∴ 四边形AMCN 是平行四边形,
由翻折得,AM=CM,
∴四边形AMCN 是菱形;
证法二:由翻折得,AN = NC,AM = MC,∠AMN=∠CMN,
∵AD∥BC,
∴ ∠ANM=∠CMN,
∴∠AMN=∠ANM,
∴AM=AN,
∴AM=MC=CN=NA,
∴ 四边形AMCN 是菱形;
(2)设菱形 AMCN 的边长为 x cm,则 BM=8-x,
在Rt△ABM中,
即
解得x=5,∴AM=5cm,
显然,当点 P 在AM 上时,点 Q 在 CD 上,此时A、C、P、Q四点不可能构成平行四边形,同理,点 P 在 AB 上时,点 Q 在 DN 或 CN 上,此时A、C、P、Q四点也不可能构成平行四边形,因此,只有点 P 在 BM 上,点 Q 在 DN 上时,才能构成平行四边形,此时PC=QA.
∵点 P 的速度为每秒5cm,点 Q 的速度为每秒4cm,运动时间为t,
∴ PC=PM+MC=PM+AM=5t,
QA=AD+CD-CQ=8+4-4t=12-4t,
∴5t=12-4t,解得
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,
5.【思路分析】(2) PB = QC 时,四边形PQCB为平行四边形;
(3)设未知数,建立方程求解.需分 PQ =CQ 和PQ=PC 两种情况讨论.
【答案解析】解: 1--a+16,∴a=21,b=16.
∵AB∥OC,A(0,12),∴c=12,∴ B(21,12),C(16,0);
(2)由题意,得AP =2t,QO=t,则 PB =21-2t,QC=16-t,
∵当PB=QC时,四边形 PQCB 是平行四边形,∴21--2t=16-t,解得t=5,∴ P(10,12),Q(5,0);
(3)当PQ=CQ时,如下图,过Q 作QN⊥AB于点N,
由题意,得PN=t,则 解得t=3.5,
∴P(7,12),Q(3.5,0).
当PQ=PC时,过P作PM⊥x轴于点M,
由题意,得QM=t,CM =16-2t,则t= 16-2t,解得
综上所述:P (7,12),Q (3.5,0);P ( 12),
1.【思路分析】点P 在OA 上运动,分别标出点P 在点O 和 P 在点 A 时 M 的位置.当点 P在点O 时,N在CA的中点位置,当点 P 在点A时,N在CM的中点位置,即N 运动的路径长
【答案解析】设 CA的中点为 E,连接EN.当点 P 在点 O 时,点N位置时点 E 的位置,当点 P 在点A时,N在如下图位置,点N 运动的路径长为 EN 的长度.
∵BP⊥PM,BP=PM,∴BA⊥AM,且BA =
2.【答案解析】作 QH⊥OA 于点 H,QG⊥OC于点G,
则易证△QHD≌△QGC(AAS)(证明过程略),
∴QD =QC = QA,∴ AH = DH= BQ=
连接 CA 交 BO 于点 N,则点 N 为 CA 的中点,MN为△ACD的中位线,
∵M为CD的中点,D 在 OA 上运动,M在中位线MN上运动,
∴运动的路径长为
3.【思路分析】作垂直于坐标轴的垂线,设点的坐标→证全等→根据题目条件列式求解.
过点 P作PE⊥x轴于点 E,过点 Q 作QF⊥x轴于点F,
设P(t,2t+4),可证△PCE≌△CQF),
∴QF=EC=1-t,CF =PE=2t+4,OF =2t+5,则Q(2t+5,1-t).
解:(1)点P 从点A到点B路径与点 Q 运动路径长相等,为
(2)令x=2t+5,y=1-t,则 当OQ⊥直线 时最小,由面积法求出 OQ 的最小值为
5【思路分析】G点在 CF 上,C 是定点,F是动点.因此分别标出当 E在点B 处时和点E在点 C 时 F 点的位置,就可得到G点路径.
【答案解析】当E在点B处时,点F在AC边上,为AC中点.
设为点 M,取 MC 中点 N,此时点 G 的起点为点 N.
当点 E 运动到点 C 时,点F 以 AC 为边的等边△ACH 的顶点 H,
此时G为CH的中点 R,
即点G运动的路径长为32
6.【答案解析】解:(1)如图:取 OA 的中点M,连接MD.
∵OA =OC,∴OM =OD,∴ ∠OMD =45°=∠ECB,∴∠AMD=135°=∠DCE,
又∵ ∠MAD + ∠ADO = 90°,∠CDE +∠ADO=90°,∴∠MAD=∠CDE,
在△AMD 和△DCE中
∴△AMD≌△DCE,∴AD=DE.
(2)连接FC、AC,作 BP⊥AD交y轴于 P.
∵∠ACB=45°,∠BCE=45°,
∴∠ACE=90°,
∵F为AE中点,∴AF=EF=FC,
∵点 F在AC 的垂直平分线上,
∵OB 垂直平分AC,∴点F在直线OB上,AC⊥CE,AC⊥OB,∴OB∥CE,
∴ 点 F 到直线 CE 的距离为定值且等于 AC,点F到CE的距离
同课章节目录
