2025年中考数学复习--因动点产生的面积问题 方法讲解及典例精析(含解析)
文档属性
| 名称 | 2025年中考数学复习--因动点产生的面积问题 方法讲解及典例精析(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 449.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 00:00:00 | ||
图片预览




文档简介
因动点产生的面积问题
由动点而生成的面积问题,是抛物线与直线结合的形式,常见的面积问题有规则图形的面积(如直角三角形、平行四边形、菱形、矩形的面积计算问题)以及不规则图形的面积计算,解决不规则图形的面积问题是中考压轴题常考的题型,此类问题计算量较大.有时也要根据题目的动点问题产生解的不确定性或多样性分类讨论。
【方法技巧】解决这类问题常用到以下与面积相关的知识:图形的割补、等积变形、等比转化等数学方法. 面积的存在性问题常见的解题策略有两类:
(1)先根据几何法确定存在性,再列方程求解,后检验方程的根.
(2)先假设关系存在,再列方程,然后根据方程的解验证假设是否正确.
解决动点产生的面积问题,常用到的知识和方法如下:
如图①,如果三角形的某一条边与坐标轴平行,计算这样“规则”的三角形的面积,直接用面积公式.
如图②、图③,三角形的三条边不与坐标轴平行的,计算这样“不规则”的三角形的面积,用“割”或“补”的方法.
计算面积用到的策略还有:
如图④,同底等高三角形的面积相等.平行线间的距离处处相等.
如图⑤,同底三角形的面积比等于高的比.
如图⑥,同高三角形的面积比等于底的比.
解这类题目要掌握几个基本图形的面积计算及基本解题思路,然后“以静制动”“转化求解”.即把动态问题变为静态问题,变为我们所熟知的模型来解.
基本模型一
中小学教育资源及组卷应用平台
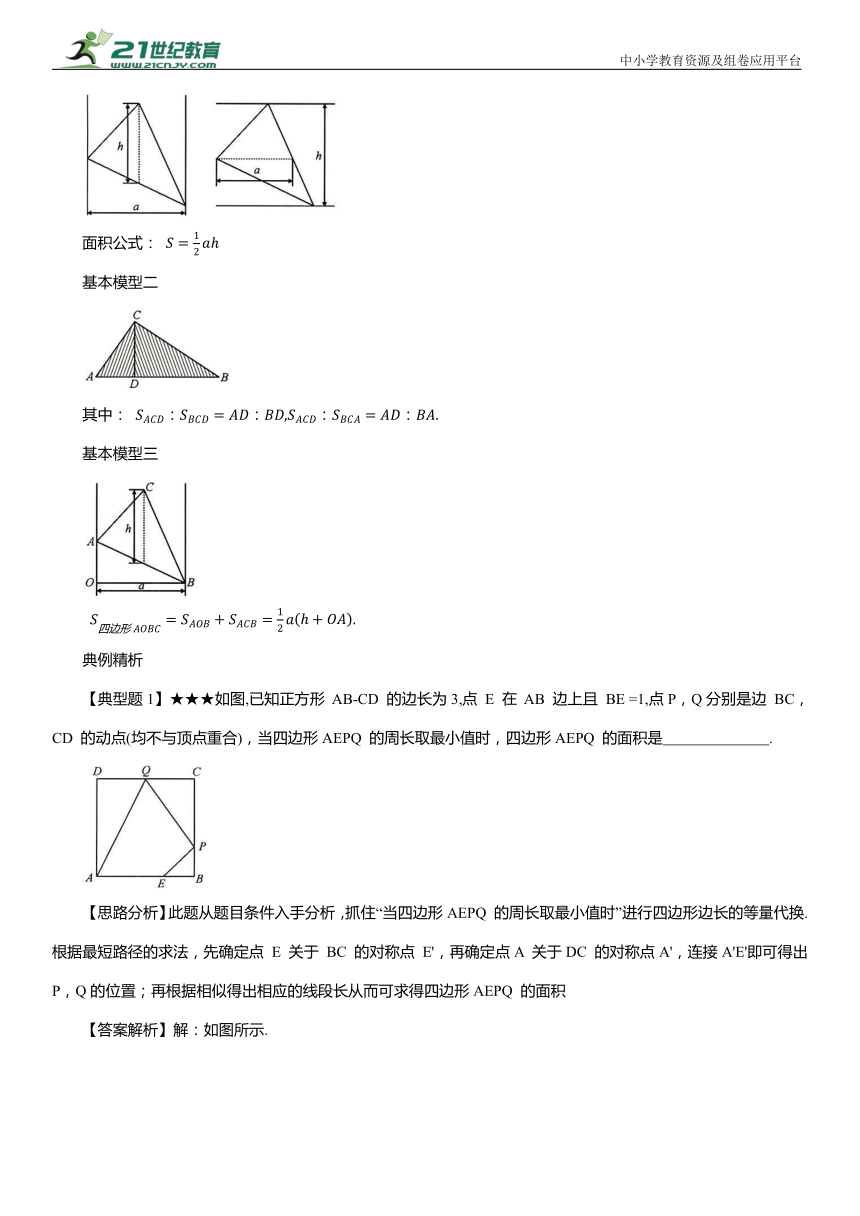
利用“铅垂高、水平宽”求三角形面积.
面积公式:
基本模型二
其中:
基本模型三
典例精析
【典型题1】★★★如图,已知正方形 AB-CD 的边长为3,点 E 在 AB 边上且 BE =1,点P,Q分别是边 BC,CD 的动点(均不与顶点重合),当四边形AEPQ 的周长取最小值时,四边形AEPQ 的面积是 .
【思路分析】此题从题目条件入手分析,抓住“当四边形AEPQ 的周长取最小值时”进行四边形边长的等量代换.根据最短路径的求法,先确定点 E 关于 BC 的对称点 E',再确定点A 关于DC 的对称点A',连接A'E'即可得出P,Q的位置;再根据相似得出相应的线段长从而可求得四边形AEPQ 的面积
【答案解析】解:如图所示.
作 E 关于 BC 的对称点 E',点 A 关于 DC的对称点 A',连接A'E',四边形 AEPQ 的周长最小.
∴AA'=6,AE'=4.
∵DQ∥AE',D 是AA'的中点,
∴ DQ 是△AA'E'的中位线,
∵BP∥AA',∴△BE'P∽△AE'A',
即
【规律总结】图形分割法是求面积的基本方法,同学们要熟练掌握.
【典型题2】★★如图,以AB为直径的⊙O的圆心O到直线l的距离OE=3,⊙O 的半径r=2,直线AB不垂直于直线l,过点A,B 分别作直线l的垂线,垂足分别为点 D,C,则四边形ABCD的面积的最大值为 .
【思路分析】表示出四边形 ABCD 的面积: 只有当CD=AB=4时,CD 最大,从而得到四边形ABCD 面积的最大值.
【答案解析】解:∵ OE⊥l,AD⊥l,BC⊥l,而OA =OB,∴OE 为直角梯形 ADCB 的中位线,
=OE·CD=3CD
当CD=AB =4时,CD 最大,四边形ABCD 的面积最大,最大值为12.
【典型题3】★★★如图,在 Rt△ABC 中,∠ACB=90°,AB=4,点 D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD 相交于点O,则△ABO 面积最大值为 .
【思路分析】题目条件有比例,因此构造三角形相似.过点 D 作 DF∥AE,推出△ABO和△ABC 面积的大小关系,转化为求△ABC 面积的最大值.
△ABC是直角三角形,同时AB 是直角三角形的斜边,于是点 C 就在以 AB 为直径的外接圆上,△ABC的最大面积就是以圆半径为高时的面积.
【答案解析】如图,过点 D 作 DF∥AE 交BE于点 F,则
∵ECE= ,∴DF=2EC,∴DO=2OC,
∵ ∠ACB=90°,∴ C 在以 AB 为直径的圆上,设圆心为M.当CM⊥AB时,△ABC 的面积最大为: 此时△ABO 的面积最大为:
【规律总结】求三角形面积最大值时,往往应用三角形外接圆求解.
【典型题4】★★★在△ABC中,若AB =6,∠ACB = 45°. 则 △ABC 面积的最大值为 .
【思路分析】利用三角形的外接圆求解.
【答案解析】作△ABC的外接圆⊙O,过C作CM⊥AB 于 M.
∵弦AB已确定,∴要使△ABC 的面积最大,只要CM取最大值即可,
如图所示,当CM过圆心O时,CM最大,
∵CM⊥AB,CM 过O,∴AM=BM(垂径定理),∴AC=BC,
∵∠AOB=2∠ACB=2×45°=90°,
∴CM=OC+OM=3 +3,
【典型题5】★★★如图,在平面直角坐标系xOy中,半径为2 的⊙O 与x轴的正半轴交于点A,点 B 是⊙O 上一动点,点 C 为弦AB 的中点,直线 与x轴、y轴分别交于点D、E,则△CDE 面积的最小值为 .
【思路分析】因为 D、E两点固定,C点是动点,因此需要确定 C点在什么位置△CDE的面积最小,B在⊙O 运动,点 C 为弦AB 的中点,那么确定 C 的轨迹就是本题的关键.
如解图,连接OB,取OA 的中点 M,连接CM,过点 M 作 MN⊥DE 于 N.首先证明点 C的运动轨迹是以 M为圆心,l为半径的⊙M,设⊙M 交 MN 于 C'.求出 MN,当点 C 与 C'重合时,△C'DE的面积最小.
【答案解析】如图,连接OB,取OA 的中点M,连接CM,过点 M作MN⊥DE于N.
∵AC=CB,AM=OM,∴MC= OB=1,
∴ 点 C 的运动轨迹是以 M为圆心,1为半径的⊙M,设⊙M交MN于C'.
∵直线 与x轴、y轴分别交于点D、E,∴D(4,0),E(0,-3),
∵ ∠MDN =∠ODE,∠MND =∠DOE,∴△DNM∽△DOE,
当点C 与C'重合时,△C'DE 的面积最小,最小值
【典型题6】★★★如图,两条抛物线y = 相交于A,B两点,点 A 在 x 轴负半轴上,且为抛物线 y 的最高点.
(1)求抛物线y 的解析式和点 B 的坐标;
(2)点C 是抛物线y 上A,B之间的一点,过点 C作x轴的垂线交y 于点 D,当线段CD取最大值时,求S△BCD.
【思路分析】(2)设点的坐标→用未知数表示出CD的长度-→ (B的横坐标--D的横坐标)列式求解.
因 是一个二次函数的关系式,利用函数的最值,求出相应的x值,及CD的最大值,进而计算出三角形的面积.
【答案解析】(1)当. 时,即 =0,解得x=2或x=-2,
又∵点A在x轴的负半轴,∴点A(-2,0),
∵点A(-2,0)是抛物线y 的最高点.
即
把A(-2,0)代入
解得
∴抛物线y 的解析式为:
由 解得,
∵A(-2,0),∴点B(3,-5),
(2)如图,
由题意得,
即:
当 时,
【典型题7】★★★如图①,在△ABC 中, ,点D,E分别在边AB,AC 上,且 AD = AE = 1,连接 DE. 现将△ADE 绕点 A 顺时针方向旋转,旋转角为α ,如图②,连接CE,BD,CD.
当0°<α<180°时,求证:CE=BD;
(2)如图③,当α=90°时,延长 CE 交 BD于点 F,求证:CF垂直平分 BD;
(3)在旋转过程中,求△BCD 的面积的最大值,并写出此时旋转角α的度数.
【思路分析】(2)利用“SAS”证得△ACE≌△ABD,推出∠ACE =∠ABD,计算得出AD 利用等腰三角形“三线合一”的性质即可得到结论;
(3)△BCD 中,边 BC 的长是定值,则 BC边上的高取最大值时△BCD的面积有最大值.
观察图形,D在以A为圆心,AD 为半径的圆上.当点 D 在线段 BC 的垂直平分线上时,△BCD的面积取得最大值,利用等腰直角三角形的性质结合三角形面积公式即可求解.
【答案解析】(1)证明:
根据题意:AB=AC,AD=AE,
∠CAB =∠EAD=90°,
∵ ∠CAE÷∠BAE=∠BAD+∠BAE=90°,
∴∠CAE=∠BAD,
在△ACE 和△ABD中,
∴△ACE≌△ABD(SAS),∴CE=BD;
(2)证明:根据题意:AB =AC,AD =AE,∠CAB=∠EAD=90°,
在△ACE 和△ABD中,
∴△ACE≌△ABD(SAS),
∴∠ACE=∠ABD,
∵∠ACE+∠AEC=90°,
且∠AEC=∠FEB,
∴∠ABD+∠FEB=90°,
∴∠EFB=90°,∴CF⊥BD,
∠CAB =∠EAD=90°,
+2,∴BC=CD,
∵CF⊥BD,∴CF 是线段 BD 的垂直平分线,即CF垂直平分BD.
(3)在△BCD 中,边 BC 的长是定值,则BC边上的高取最大值时△BCD 的面积有最大值,
∵ D 在以A为圆心,AD 为半径的圆上
∴ 当点 D 在线段 BC 的垂直平分线上时,△BCD 的面积取得最大值,如图,
=∠EAD=90°,DG⊥BC于G,
∴ △BCD 的面积的最大值为:
旋转角α=135°.
【典型题8】★★★如图,在平面直角坐标系中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),C(3,1)抛物线 -2的图象过C点,交y轴于点 D.
(1)直接写出点 D的坐标及b的值;
(2)平移该抛物线的对称轴所在直线l,设l与x轴交于点G(x,0),当OG等于多少时,恰好将△ABC的面积分为相等的两部分
【思路分析】(2)需画出图形,转化为我们所熟知的三角形△CFG的面积求解.
【答案解析】(1)D(0,-2).
将C(3,1)代入抛物线 得
∴二次函数解析式为
(2)在 Rt△AOB 中,由勾股定理得:AB = 所以
设直线 BC、直线 AC 的解析式为
将A(1,0),B(0,2),C(3,1)代入得:
解得
即
如图所示. 设直线l交直线 BC、直线 AC于点F、G. 过C作CH⊥l于点 H.
因为 G(x,0),所以 所以 -x,由 得 即: 解得 (舍),
所以OG等于 时,恰好将△ABC 的面积分为相等的两部分.
【典型题9】★★★如图,在平面直角坐标系中,抛物线 与直线 交于A、B两点,已知点 B 的横坐标是4,直线 与x、y轴的交点分别为A、C,点P 是抛物线上一个动点.
(1)求抛物线的解析式;
(2)若点 P 在直线 的上方,求△PAC的最大面积.
【思路分析】(2)利用两三角形的高相等,则面积比等于底的比,将题目中的三角形转化为我们熟知的三顶点都在抛物线上的三角形,利用铅垂高、水平宽求解.
【答案解析】(1)因为点 B 的横坐标是4,所以B(4,-2),A(-1,0),C(0,- ).
将A(-1,0)、B(4,-2)代入 +c得:
解得
即抛物线的解析式为:
(2)如图,过点 B 作 BH⊥x轴于点 H. 过P作PG⊥x轴于点 G,交AB 于点 E,连接PB.
由勾股定理得:
即
设P 点横坐标为m,则
∴当 时,△PAC 的面积有最大值,最大值为
【典型题10】★★★★如图①,平面直角坐标系xOy中,等腰△ABC 的底边 BC 在x轴上,BC=8,顶点A在y的正半轴上,OA=2,一动点E从(3,0)出发,以每秒1个单位的速度沿 CB向左运动,到达OB 的中点停止.另一动点 F 从点 C 出发,以相同的速度沿 CB 向左运动,到达点 O 停止.已知点 E、F同时出发,以EF为边作正方形 EFGH,使正方形 EFGH 和△ABC在BC 的同侧,设运动的时间为 t 秒(t≥0).
(1)当点H落在AC边上时,求t的值;
(2)设正方形 EFGH 与△ABC 重叠面积为S,请问是否存在t值,使得 若存在,求出t值;若不存在,请说明理由;
(3)如图②,取AC 的中点 D,连接OD,当点 E、F开始运动时,点M从点O 出发,以每秒2 个单位的速度沿 OD-DC-CD-DO 运动,到达点 O 后停止运动并消失.请问在点 E的整个运动过程中,点M 可能在正方形 EFGH内(含边界)吗 如果可能,求出点 M 在正方形 EFGH内(含边界)的时长;若不可能,请说明理由.
【思路分析】(1)点H落在AC边上时,根据平行线段成比例列式,也可根据tan∠ACO = 得出EH=EF=1,EC=2,t=1.
(2)由题意,当点F运动到点 O 停止运动前,重叠面积最大是边长为1的正方形面积,此时不存在t,因此t>4,重叠部分是五边形OEKJG.构建方程求解即可,详见解析.
(3)本题关键要得出点 M 在水平方向的运动速度是2 ·cos∠DOC =4,然后分别求出点M 落在正方形的边 EH 和 FG 时t 的值,两者之差就是时长,注意M点两次落在EH 和FG上.
【答案解析】(1)如图,
由题意得,OA =2,OB =OC =4,EF =EH=FG=HG=1,
当点H落在AC上时,∵EH∥OA,
点 E的运动路程为1,
∴t=1时,点H落在AC 上.
(2)由题意,如图,当点 F运动到点 O 停止运动前,重叠面积最大是边长为1 的正方形面积,此时不存在t,因此t>4,E到达OB的中点停止,t<5,重叠部分是五边形OEKJG.
∵正方形 EFGH 与△ABC 重叠面积为
∴此时点 F 与O 重合,已经停止运动,图中重叠部分是五边形OEKJG.
由题意:∵HG∥OB,∴∠HJK=∠ABO,
∵HG∥OB,EO=t-3,∴HIBE=HER,即 解得
整理得
解得 或 舍弃),∴满足条件的t值为
(3)如图,根据题意,易求得 D 的坐标为(2,1), 点 M 在水平方向的运动速度是 ,然后分别求出点 M 落在正方形的边EH和FG时t的值,两者之差就是时长,注意 M 点两次落在 EH 和 FG上.
当点 M 第一次落在EH上时,3-t=4t,
当点 M第一次落在FG上时,4-t=4t,
∴点M 第一次落在正方形内部(包括边界)的时长
当点M第二次落在FG上时,4t-t=4,
当点 M第二次落在 EH 上时,4t-(t+1)
点 M 第二次落在正方形内部(包括边界)的时长
∴点 M 落在正方形内部(包括边界)的总时长
由动点而生成的面积问题,是抛物线与直线结合的形式,常见的面积问题有规则图形的面积(如直角三角形、平行四边形、菱形、矩形的面积计算问题)以及不规则图形的面积计算,解决不规则图形的面积问题是中考压轴题常考的题型,此类问题计算量较大.有时也要根据题目的动点问题产生解的不确定性或多样性分类讨论。
【方法技巧】解决这类问题常用到以下与面积相关的知识:图形的割补、等积变形、等比转化等数学方法. 面积的存在性问题常见的解题策略有两类:
(1)先根据几何法确定存在性,再列方程求解,后检验方程的根.
(2)先假设关系存在,再列方程,然后根据方程的解验证假设是否正确.
解决动点产生的面积问题,常用到的知识和方法如下:
如图①,如果三角形的某一条边与坐标轴平行,计算这样“规则”的三角形的面积,直接用面积公式.
如图②、图③,三角形的三条边不与坐标轴平行的,计算这样“不规则”的三角形的面积,用“割”或“补”的方法.
计算面积用到的策略还有:
如图④,同底等高三角形的面积相等.平行线间的距离处处相等.
如图⑤,同底三角形的面积比等于高的比.
如图⑥,同高三角形的面积比等于底的比.
解这类题目要掌握几个基本图形的面积计算及基本解题思路,然后“以静制动”“转化求解”.即把动态问题变为静态问题,变为我们所熟知的模型来解.
基本模型一
中小学教育资源及组卷应用平台
利用“铅垂高、水平宽”求三角形面积.
面积公式:
基本模型二
其中:
基本模型三
典例精析
【典型题1】★★★如图,已知正方形 AB-CD 的边长为3,点 E 在 AB 边上且 BE =1,点P,Q分别是边 BC,CD 的动点(均不与顶点重合),当四边形AEPQ 的周长取最小值时,四边形AEPQ 的面积是 .
【思路分析】此题从题目条件入手分析,抓住“当四边形AEPQ 的周长取最小值时”进行四边形边长的等量代换.根据最短路径的求法,先确定点 E 关于 BC 的对称点 E',再确定点A 关于DC 的对称点A',连接A'E'即可得出P,Q的位置;再根据相似得出相应的线段长从而可求得四边形AEPQ 的面积
【答案解析】解:如图所示.
作 E 关于 BC 的对称点 E',点 A 关于 DC的对称点 A',连接A'E',四边形 AEPQ 的周长最小.
∴AA'=6,AE'=4.
∵DQ∥AE',D 是AA'的中点,
∴ DQ 是△AA'E'的中位线,
∵BP∥AA',∴△BE'P∽△AE'A',
即
【规律总结】图形分割法是求面积的基本方法,同学们要熟练掌握.
【典型题2】★★如图,以AB为直径的⊙O的圆心O到直线l的距离OE=3,⊙O 的半径r=2,直线AB不垂直于直线l,过点A,B 分别作直线l的垂线,垂足分别为点 D,C,则四边形ABCD的面积的最大值为 .
【思路分析】表示出四边形 ABCD 的面积: 只有当CD=AB=4时,CD 最大,从而得到四边形ABCD 面积的最大值.
【答案解析】解:∵ OE⊥l,AD⊥l,BC⊥l,而OA =OB,∴OE 为直角梯形 ADCB 的中位线,
=OE·CD=3CD
当CD=AB =4时,CD 最大,四边形ABCD 的面积最大,最大值为12.
【典型题3】★★★如图,在 Rt△ABC 中,∠ACB=90°,AB=4,点 D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD 相交于点O,则△ABO 面积最大值为 .
【思路分析】题目条件有比例,因此构造三角形相似.过点 D 作 DF∥AE,推出△ABO和△ABC 面积的大小关系,转化为求△ABC 面积的最大值.
△ABC是直角三角形,同时AB 是直角三角形的斜边,于是点 C 就在以 AB 为直径的外接圆上,△ABC的最大面积就是以圆半径为高时的面积.
【答案解析】如图,过点 D 作 DF∥AE 交BE于点 F,则
∵ECE= ,∴DF=2EC,∴DO=2OC,
∵ ∠ACB=90°,∴ C 在以 AB 为直径的圆上,设圆心为M.当CM⊥AB时,△ABC 的面积最大为: 此时△ABO 的面积最大为:
【规律总结】求三角形面积最大值时,往往应用三角形外接圆求解.
【典型题4】★★★在△ABC中,若AB =6,∠ACB = 45°. 则 △ABC 面积的最大值为 .
【思路分析】利用三角形的外接圆求解.
【答案解析】作△ABC的外接圆⊙O,过C作CM⊥AB 于 M.
∵弦AB已确定,∴要使△ABC 的面积最大,只要CM取最大值即可,
如图所示,当CM过圆心O时,CM最大,
∵CM⊥AB,CM 过O,∴AM=BM(垂径定理),∴AC=BC,
∵∠AOB=2∠ACB=2×45°=90°,
∴CM=OC+OM=3 +3,
【典型题5】★★★如图,在平面直角坐标系xOy中,半径为2 的⊙O 与x轴的正半轴交于点A,点 B 是⊙O 上一动点,点 C 为弦AB 的中点,直线 与x轴、y轴分别交于点D、E,则△CDE 面积的最小值为 .
【思路分析】因为 D、E两点固定,C点是动点,因此需要确定 C点在什么位置△CDE的面积最小,B在⊙O 运动,点 C 为弦AB 的中点,那么确定 C 的轨迹就是本题的关键.
如解图,连接OB,取OA 的中点 M,连接CM,过点 M 作 MN⊥DE 于 N.首先证明点 C的运动轨迹是以 M为圆心,l为半径的⊙M,设⊙M 交 MN 于 C'.求出 MN,当点 C 与 C'重合时,△C'DE的面积最小.
【答案解析】如图,连接OB,取OA 的中点M,连接CM,过点 M作MN⊥DE于N.
∵AC=CB,AM=OM,∴MC= OB=1,
∴ 点 C 的运动轨迹是以 M为圆心,1为半径的⊙M,设⊙M交MN于C'.
∵直线 与x轴、y轴分别交于点D、E,∴D(4,0),E(0,-3),
∵ ∠MDN =∠ODE,∠MND =∠DOE,∴△DNM∽△DOE,
当点C 与C'重合时,△C'DE 的面积最小,最小值
【典型题6】★★★如图,两条抛物线y = 相交于A,B两点,点 A 在 x 轴负半轴上,且为抛物线 y 的最高点.
(1)求抛物线y 的解析式和点 B 的坐标;
(2)点C 是抛物线y 上A,B之间的一点,过点 C作x轴的垂线交y 于点 D,当线段CD取最大值时,求S△BCD.
【思路分析】(2)设点的坐标→用未知数表示出CD的长度-→ (B的横坐标--D的横坐标)列式求解.
因 是一个二次函数的关系式,利用函数的最值,求出相应的x值,及CD的最大值,进而计算出三角形的面积.
【答案解析】(1)当. 时,即 =0,解得x=2或x=-2,
又∵点A在x轴的负半轴,∴点A(-2,0),
∵点A(-2,0)是抛物线y 的最高点.
即
把A(-2,0)代入
解得
∴抛物线y 的解析式为:
由 解得,
∵A(-2,0),∴点B(3,-5),
(2)如图,
由题意得,
即:
当 时,
【典型题7】★★★如图①,在△ABC 中, ,点D,E分别在边AB,AC 上,且 AD = AE = 1,连接 DE. 现将△ADE 绕点 A 顺时针方向旋转,旋转角为α ,如图②,连接CE,BD,CD.
当0°<α<180°时,求证:CE=BD;
(2)如图③,当α=90°时,延长 CE 交 BD于点 F,求证:CF垂直平分 BD;
(3)在旋转过程中,求△BCD 的面积的最大值,并写出此时旋转角α的度数.
【思路分析】(2)利用“SAS”证得△ACE≌△ABD,推出∠ACE =∠ABD,计算得出AD 利用等腰三角形“三线合一”的性质即可得到结论;
(3)△BCD 中,边 BC 的长是定值,则 BC边上的高取最大值时△BCD的面积有最大值.
观察图形,D在以A为圆心,AD 为半径的圆上.当点 D 在线段 BC 的垂直平分线上时,△BCD的面积取得最大值,利用等腰直角三角形的性质结合三角形面积公式即可求解.
【答案解析】(1)证明:
根据题意:AB=AC,AD=AE,
∠CAB =∠EAD=90°,
∵ ∠CAE÷∠BAE=∠BAD+∠BAE=90°,
∴∠CAE=∠BAD,
在△ACE 和△ABD中,
∴△ACE≌△ABD(SAS),∴CE=BD;
(2)证明:根据题意:AB =AC,AD =AE,∠CAB=∠EAD=90°,
在△ACE 和△ABD中,
∴△ACE≌△ABD(SAS),
∴∠ACE=∠ABD,
∵∠ACE+∠AEC=90°,
且∠AEC=∠FEB,
∴∠ABD+∠FEB=90°,
∴∠EFB=90°,∴CF⊥BD,
∠CAB =∠EAD=90°,
+2,∴BC=CD,
∵CF⊥BD,∴CF 是线段 BD 的垂直平分线,即CF垂直平分BD.
(3)在△BCD 中,边 BC 的长是定值,则BC边上的高取最大值时△BCD 的面积有最大值,
∵ D 在以A为圆心,AD 为半径的圆上
∴ 当点 D 在线段 BC 的垂直平分线上时,△BCD 的面积取得最大值,如图,
=∠EAD=90°,DG⊥BC于G,
∴ △BCD 的面积的最大值为:
旋转角α=135°.
【典型题8】★★★如图,在平面直角坐标系中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),C(3,1)抛物线 -2的图象过C点,交y轴于点 D.
(1)直接写出点 D的坐标及b的值;
(2)平移该抛物线的对称轴所在直线l,设l与x轴交于点G(x,0),当OG等于多少时,恰好将△ABC的面积分为相等的两部分
【思路分析】(2)需画出图形,转化为我们所熟知的三角形△CFG的面积求解.
【答案解析】(1)D(0,-2).
将C(3,1)代入抛物线 得
∴二次函数解析式为
(2)在 Rt△AOB 中,由勾股定理得:AB = 所以
设直线 BC、直线 AC 的解析式为
将A(1,0),B(0,2),C(3,1)代入得:
解得
即
如图所示. 设直线l交直线 BC、直线 AC于点F、G. 过C作CH⊥l于点 H.
因为 G(x,0),所以 所以 -x,由 得 即: 解得 (舍),
所以OG等于 时,恰好将△ABC 的面积分为相等的两部分.
【典型题9】★★★如图,在平面直角坐标系中,抛物线 与直线 交于A、B两点,已知点 B 的横坐标是4,直线 与x、y轴的交点分别为A、C,点P 是抛物线上一个动点.
(1)求抛物线的解析式;
(2)若点 P 在直线 的上方,求△PAC的最大面积.
【思路分析】(2)利用两三角形的高相等,则面积比等于底的比,将题目中的三角形转化为我们熟知的三顶点都在抛物线上的三角形,利用铅垂高、水平宽求解.
【答案解析】(1)因为点 B 的横坐标是4,所以B(4,-2),A(-1,0),C(0,- ).
将A(-1,0)、B(4,-2)代入 +c得:
解得
即抛物线的解析式为:
(2)如图,过点 B 作 BH⊥x轴于点 H. 过P作PG⊥x轴于点 G,交AB 于点 E,连接PB.
由勾股定理得:
即
设P 点横坐标为m,则
∴当 时,△PAC 的面积有最大值,最大值为
【典型题10】★★★★如图①,平面直角坐标系xOy中,等腰△ABC 的底边 BC 在x轴上,BC=8,顶点A在y的正半轴上,OA=2,一动点E从(3,0)出发,以每秒1个单位的速度沿 CB向左运动,到达OB 的中点停止.另一动点 F 从点 C 出发,以相同的速度沿 CB 向左运动,到达点 O 停止.已知点 E、F同时出发,以EF为边作正方形 EFGH,使正方形 EFGH 和△ABC在BC 的同侧,设运动的时间为 t 秒(t≥0).
(1)当点H落在AC边上时,求t的值;
(2)设正方形 EFGH 与△ABC 重叠面积为S,请问是否存在t值,使得 若存在,求出t值;若不存在,请说明理由;
(3)如图②,取AC 的中点 D,连接OD,当点 E、F开始运动时,点M从点O 出发,以每秒2 个单位的速度沿 OD-DC-CD-DO 运动,到达点 O 后停止运动并消失.请问在点 E的整个运动过程中,点M 可能在正方形 EFGH内(含边界)吗 如果可能,求出点 M 在正方形 EFGH内(含边界)的时长;若不可能,请说明理由.
【思路分析】(1)点H落在AC边上时,根据平行线段成比例列式,也可根据tan∠ACO = 得出EH=EF=1,EC=2,t=1.
(2)由题意,当点F运动到点 O 停止运动前,重叠面积最大是边长为1的正方形面积,此时不存在t,因此t>4,重叠部分是五边形OEKJG.构建方程求解即可,详见解析.
(3)本题关键要得出点 M 在水平方向的运动速度是2 ·cos∠DOC =4,然后分别求出点M 落在正方形的边 EH 和 FG 时t 的值,两者之差就是时长,注意M点两次落在EH 和FG上.
【答案解析】(1)如图,
由题意得,OA =2,OB =OC =4,EF =EH=FG=HG=1,
当点H落在AC上时,∵EH∥OA,
点 E的运动路程为1,
∴t=1时,点H落在AC 上.
(2)由题意,如图,当点 F运动到点 O 停止运动前,重叠面积最大是边长为1 的正方形面积,此时不存在t,因此t>4,E到达OB的中点停止,t<5,重叠部分是五边形OEKJG.
∵正方形 EFGH 与△ABC 重叠面积为
∴此时点 F 与O 重合,已经停止运动,图中重叠部分是五边形OEKJG.
由题意:∵HG∥OB,∴∠HJK=∠ABO,
∵HG∥OB,EO=t-3,∴HIBE=HER,即 解得
整理得
解得 或 舍弃),∴满足条件的t值为
(3)如图,根据题意,易求得 D 的坐标为(2,1), 点 M 在水平方向的运动速度是 ,然后分别求出点 M 落在正方形的边EH和FG时t的值,两者之差就是时长,注意 M 点两次落在 EH 和 FG上.
当点 M 第一次落在EH上时,3-t=4t,
当点 M第一次落在FG上时,4-t=4t,
∴点M 第一次落在正方形内部(包括边界)的时长
当点M第二次落在FG上时,4t-t=4,
当点 M第二次落在 EH 上时,4t-(t+1)
点 M 第二次落在正方形内部(包括边界)的时长
∴点 M 落在正方形内部(包括边界)的总时长
同课章节目录
