2025年中考数学复习--线、面的动点最值巩固练习(含解析)
文档属性
| 名称 | 2025年中考数学复习--线、面的动点最值巩固练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 06:23:29 | ||
图片预览




文档简介
线、面的动点最值巩固练习
【巩固练习1】
已知线段AB =12,CD =6,线段 CD 在直线AB上运动(点A 在 B,C 左侧,点 C 在点 D左侧).
(1)点M,N分别是线段AC,BD 的中点,若BC=4,求MN的长;
(2)当CD 运动到D 点与 B 点重合时,点P 是线段AB 延长线上一点,下列两个结论:是定值; 是定值,请作出正确的选择,并求出其定值.
【巩固练习2】
数轴上两个点A,B所对应的数为-8,7,M,N为数轴上的两点,表示的数分别为m,m+3.
(1)如图①,若AM = BN,直接写出 M,N点对应的数;
(2)若AN=2BM,求出m的值;
中小学教育资源及组卷应用平台
(3)若P 为AN的中点,点 Q 为 BM 的中点,问当m的值发生变化时,PQ 的值是否发生改变 如果不变,求出 PQ 的值;如果改变,说明理由.
【巩固练习3】
如图,C 为线段AB 上一点,且AC=2BC,AC 的 比BC小5.
(1)求AC,BC的长;
(2)点P从A点出发,以1个单位/秒的速度在线段AB 上向 B 点运动,设运动时间为 t秒(t<10),D 为PB的中点,E 为PC 的中点若 试求点 P 运动时间t的值;
(3)若P从A点出发,以1个单位/秒的速度在线段AB 上向 B 点运动,同时点 Q 从 B 点出发,以 个单位/秒的速度在 AB 的延长线上与P 点同向运动,运动时间t<30,D 为 PB的中点,F为DQ 的中点,E在PB 上且 PB,当P,Q两点运动的过程中,给出下面两个结论:①DE+DF 的值不变;②|DE-DF| 的值不变,其中只有一个结论是正确的,请判断正确的结论并求其值.
【巩固练习4】
如图,在射线OG上有三点A,B,C,满足OA=40 cm,AB=60 cm,BC=10 cm,点 P 从点O 出发,沿射线 OG 以 1 cm/s 的速度匀速运动,点Q 从点 C 出发沿射线 CO 匀速运动,其中点 P 和点 Q 两点同时出发,且P 运动到 B处时,P,Q停止运动.
(1)当P,Q 相遇时,有 PA=2PB,求点 Q的运动速度;
(2)若点 Q 的运动速度为3c m/s,则经过多长时间 P,Q两点相距70 cm;
(3)线段MN=10cm(N在M右侧),M与A 重合,线段 MN 从A 点出发,沿射线 AG 以2cm /s的速度匀速运动,若点 Q的运动速度为3c m/s,且P,Q,M,N同时运动,设运动时间为 ts,是否存在这样的t 值使得|MQ - PN| =2OP 若存在,求出t值;若不存在,说明理由.
【巩固练习5】
如图①,已知a,b满足( =0,c=2a+3b.且有理数a,b,c在数轴上对应的点分别为A,B,C.
(1)则a= ,b= ,c= ;
(2)点D 是数轴上A 点右侧一动点,点E,点F分别为CD,AD 中点,当点D 运动时,线段EF 的长度是否发生变化 若变化,请说明理由,若不变,请求出其值;
(3)若点A,B,C在数轴上运动,其中点 C以每秒1个单位的速度向左运动,同时点A 和点B 分别以每秒3 个单位和每秒2个单位的速度向右运动,请问:是否存在一个常数m使m·AB-2BC不随运动时间t的改变而改变 若存在,请求出m 和这个不变化的值;若不存在,请说明理由.
【巩固练习6】
点A 在数轴上对应的数为a,点B 对应的数为b,且a,b满足
(1)求线段AB 的长;
(2)点C 在数轴上对应的数为x,且x是方程 的根,在数轴上是否存在点 P,使得PA+PB=PC 若存在,直接写出点 P 对应的数;若不存在,说明理由;
(3)动点 P 从点A 出发,以每秒6个单位长度的速度沿数轴向左匀速运动;动点 Q 从点B出发,以每秒4个单位长度的速度沿数轴向左匀速移动;动点 M 从点 A 出发,以每秒3个单位长度的速度沿数轴向左匀速移动,设运动时间为t秒,当t<7时, 的值是否发生变化 若不变求出其值;若变化,写出范围.
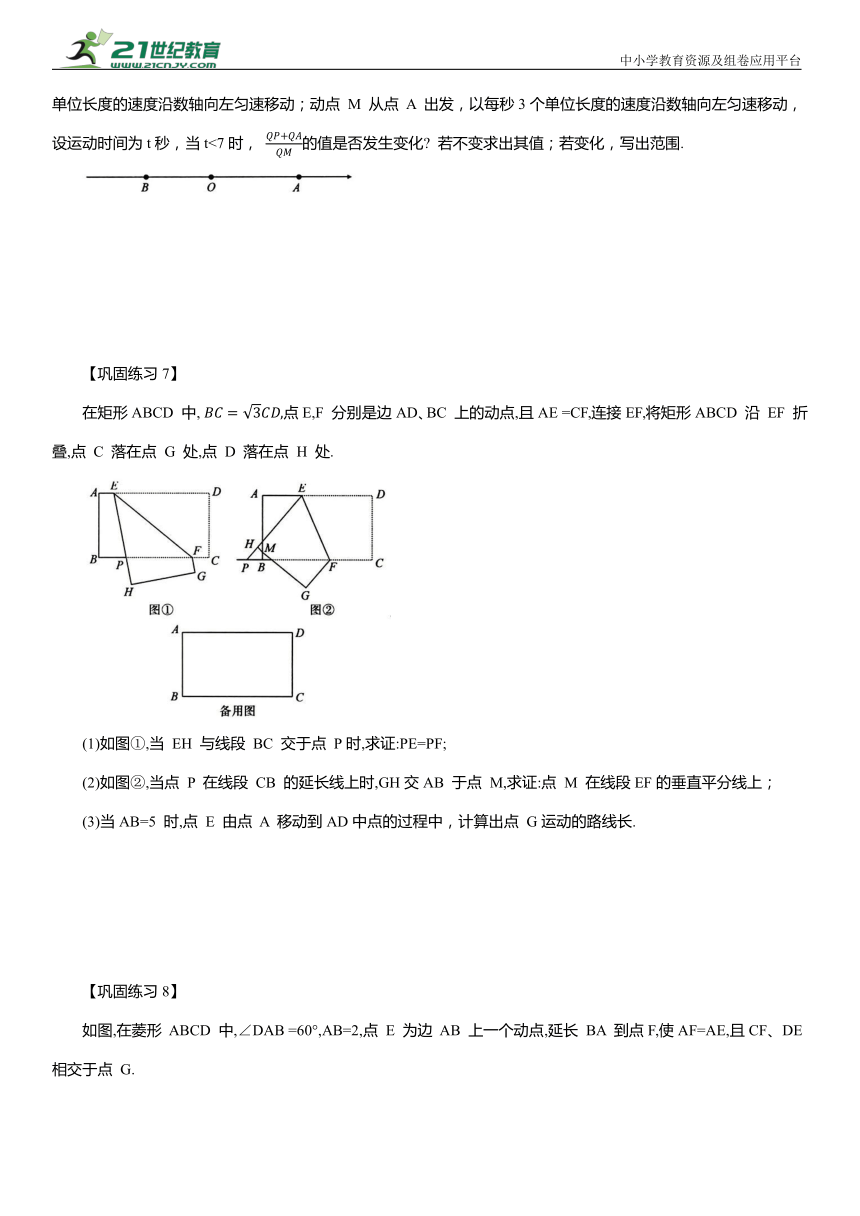
【巩固练习7】
在矩形ABCD 中, 点E,F 分别是边AD、BC 上的动点,且AE =CF,连接EF,将矩形ABCD 沿 EF 折叠,点 C 落在点 G 处,点 D 落在点 H 处.
(1)如图①,当 EH 与线段 BC 交于点 P时,求证:PE=PF;
(2)如图②,当点 P 在线段 CB 的延长线上时,GH交AB 于点 M,求证:点 M 在线段EF的垂直平分线上;
(3)当AB=5 时,点 E 由点 A 移动到AD中点的过程中,计算出点 G运动的路线长.
【巩固练习8】
如图,在菱形 ABCD 中,∠DAB =60°,AB=2,点 E 为边 AB 上一个动点,延长 BA 到点F,使AF=AE,且CF、DE 相交于点 G.
(1)当点 E运动到AB中点时,证明:四边形DFEC 是平行四边形;
(2)当CG=2时,求AE的长;
(3)当点 E 从点 A 开始向右运动到点 B时,求点 G运动路径的长度.
【巩固练习9】
在数学兴趣小组活动中,小亮进行数学探究活动.
(1)△ABC 是边长为3 的等边三角形,E是边AC 上的一点,且AE=1,小亮以BE 为边作等边三角形BEF,如图①,求 CF 的长;
(2)△ABC 是边长为3 的等边三角形,E是边AC 上的一个动点,小亮以 BE 为边作等边三角形 BEF,如图②,在点 E 从点 C 到点 A的运动过程中,求点 F 所经过的路径长;
(3)△ABC 是边长为3的等边三角形,M是高 CD 上的一个动点,小亮以 BM 为边作等边三角形 BMN,如图③,在点 M 从点 C 到点 D的运动过程中,求点 N 所经过的路径长;
(4)正方形ABCD 的边长为3,E 是边 CB上的一个动点,在点E 从点 C 到点B 的运动过程中,小亮以 B 为顶点作正方形 BFGH,其中点 F、G都在直线AE 上,如图④,当点 E 到达点B时,点F、G、H与点B重合.则点H所经过的路径长为 ,点G所经过的路径长为
【巩固练习10】
如图,四边形ABCD 为矩形,AB=3,BC=4,P、Q 均从点B 出发,点 P 以2个单位每秒的速度沿 BA-AC 的方向运动,点 Q 以1个单位每秒的速度沿 BC-CD 运动,设运动时间为t秒.
(1)求AC 的长;
(2)若 求S关于t的解析式.
【巩固练习11】
如图①,E、F 是等腰 Rt△ABC 的斜边 BC上的两动点,∠EAF = 45°,CD ⊥BC 且 CD=BE.
(1)求证:△ABE≌△ACD;
(2)求证:
(3)如图②,作 AH⊥BC,垂足为 H,设∠EAH=α,∠FAH=β,不妨设 请利用(2)的结论证明:当α+β=45°时, tan(α+β) 成立.
【巩固练习12】
如图,在 Rt△ABC 中,点 P 为斜边 BC 上一动点,将△ABP 沿直线 AP 折叠,使得点 B 的对应点为B',连接AB',BB',PB'.
(1)如图①,若PB'⊥AC,证明:
(2)如图②,若 AB = AC,BP =3PC,求cos∠B'AC的值;
(3)如图③,若∠ACB=30°,是否存在点P,使得AB=CB'.若存在,求此时 的值;若不存在,请说明理由.
【巩固练习13】
已知四边形ABCD 是边长为1 的正方形,点 E 是射线BC 上的动点,以AE 为直角边在直线 BC 的上方作等腰直角三角形 AEF,∠AEF=90°,设BE=m.
(1)如图①,若点 E在线段BC 上运动,EF交 CD 于点 P,AF 交 CD 于点 Q,连接CF,
①当 时,求线段CF 的长;
②在△PQE'中,设边QE 上的高为h,请用含m的代数式表示h,并求h的最大值;
(2)设过BC 的中点且垂直于 BC 的直线被等腰直角三角形AEF 截得的线段长为y,请直接写出y与m的关系式.
【巩固练习14】
如图 ①,已 知 ∠RPQ = 45°, △ABC 中∠ACB=90°,动点 P 从点 A 出发,以: 的速度在线段AC 上向点 C 运动,PQ,PR分别与射线AB交于E,F两点,且PE⊥AB,当点 P与点 C 重合时停止运动,如图②,设点 P 的运动时间为 xs,∠RPQ 与△ABC 的重叠部分面积为ycm ,y与x的函数关系由 和 两段不同的图象组成.
(1)填空:①当x=5s时,EF= cm;②sinA = ;
(2)求y与x的函数关系式,并写出x的取值范围;
(3)当 时,请直接写出x的取值范围.
【巩固练习15】
如图①,抛物线 经过A(-1,0),B(4,0) 两点,与y 轴交于点 C,连接BC.
(1)求该抛物线的函数表达式;
(2)如图②,直线l :y= kx+3 经过点 A,点 P 为直线l上的一个动点,且位于x 轴的上方,点Q 为抛物线上的一个动点,当PQ//y轴时,作QM⊥PQ,交抛物线于点 M (点 M 在点Q 的右侧),以 PQ,QM 为邻边构造矩形PQMN,求该矩形周长的最小值;
(3)如图③,设抛物线的顶点为 D,在(2)的条件下,当矩形 PQMN 的周长取最小值时,抛物线上是否存在点 F,使得 若存在,请求出点 F 的坐标;若不存在,请说明理由.
1.(1)当点 C在点B 右侧时,如图(1),
∵M,N分别为线段AC,BD 的中点,
当点C在点 B 左侧时,如图(2),
∵M,N 分别为线段AC,BD 的中点,
综上所述,MN 的长为9.
(2)①正确, 理由如下:
是定值,定值为2.
而-8+6=-2,7--6=1,
∴M、N点对应的数分别是-2和1;
(2)∵A、B所对应的数分别是-8、7, M、N所对应的数分别是m、 m+3.
∴AN=|(m+3)-(-8)|=|m+11|, BM =|7-m|,
①当m≤–11时, 有m+11≤0, 7–m>0.
∴AN=|m+11|=-m--11, BM =|7-m|=7-m,由AN=2BM得, - m--11=2(7-m),
解得m=25,
∵m≤-11,
∴m=25不合题意, 舍去.
②当-110, 7-m≥0.
∴AN=|m+11|=m+11, BM=|7-m|=7-m,由
AN =2BM得, m+11=2(7-m),解得m=1.
③当m>7时, 有m+11>0, 7-m<0.
∴AN=|m+11|=m+11, BM=|7-m|=m﹣7,
由AN=2BM得, m+11=2(m﹣7),
解得m=25,
综上所述: 当m=1或m=25时, AN =2BM.
(3)PQ的值不发生改变.
设P、Q表示的数为a、b.
∵点P为AN的中点,
①当点N在点A右侧时,点A,N表示的数分别为
解得
同理可得,
②当点N在点A左侧时,同理可得
∴PQ的值不发生改变,恒为6.
3.(1) 设 则
由题意得:
解得:
又∵D为PB的中点,.
∵ D为PB的中点, E为PC的中点,
又∵
解得:
(3)结论①正确, 值为: 理由如下:
设运动时间为t,
则
又∵F为DQ的中点,
4.(1)由题意可知, 若P在线段OA上, PA< PB, 不合题意舍去;
若P在线段AB上, PA+PB=60
∵PA=2PB
∴PB=20, OP=80
运动时间为t = 80s
∴点Q的运动速度为
故答案为:
(2)相遇前P, Q相距70cm, 得(1+3)t=110-70
∴t=10
相遇后P, Q相距70cm, 得(1+3)t=110+70
∴t=45
∴经过10s或45s, P, Q相距70cm;
故答案为: 10s或45s
(3)取O为数轴原点, 运动 ts后M对应的数为40﹢2t,N对应的数为50﹢2t, Q对应的数为110﹣3t, P对应的数为t,
∴MQ=|5t﹣70|, PN =50﹢t, OP=t
当MQ﹣PN=2OP时, 有|5t﹣70|﹣(50﹢t)=2t
∴t=60或
当PN﹣MQ=2OP时,有(50﹢t)﹣|5t﹣70|=2t
∴t=20或t=5
综上所述,存在这样的t,t值为 或5s或20s或60s
故答案为:t值为 或5s或20s或60s
5.(1)∵a、 b满足
∴a--2=0且 ab+6=0.
解得a=2, b=-3.
∴c=2a+3b=-5.
故答案为: 2, - 3, - 5
(2)如图, 当点 D 运动时, 线段
EF的长度不发生变化,理由如下:
∵点E.点 F分别为CD、 AD中点,
∴当点D 运动时,线段EF的长度不发生变化,其值为3.5;
(3)假设存在常数m使得m·AB--2BC 不随运动时间t的改变而改变。
则依题意得: AB=5+t, 2BC=4+6t.
所以m·AB﹣2BC=m(5﹢t)﹣(4﹢6t)=5m+ mt-4-6t 与t的值无关, 即m--6=0,
解得m=6,
6.(1) 由题意可知:
∴C对应的数为5,
当P在B左侧时,此时
故不满足题意,当P在AB之间时,此时
故不满足题意,
当P在A的右侧时,此时
故不满足题意,
故不存点P使得,
∴点P在点Q的右侧时,点Q、P、M三点在数轴上的位置依次从左向右,
则有:
7.(1)证明: 如图1中,
∵四边形ABCD是矩形,
由翻折变换可知,
(2)证明: 如图2中, 连接AC交EF于O, 连接PM, PO.
由折叠的性质可知ED=EH, 所以BF=EH,
∴PE﹣EH = PF﹣BF,
∴PB=PH,
∵∠PHM =∠PBM =90°, PM = PM,
∴Rt△PMH≌Rt△PMB(HL),
∴PM平分∠EPF,
∴点M在线段EF的垂直平分线上.
(3)如图3中,由题意,点E由点A移动到AD中点的过程中,点G运动的路径是图中弧BC.
在Rt△BCD中,
∴∠CBD=30°,
∴∠ABO=∠OAB =60°,
∴△AOB是等边三角形,
∴OA=OD=OB=OC=AB=5, ∠BOC=120°,
∴点G运动的路径的长
故答案为:
8.(1)证明: 连接DF, CE, 如图所示:
∵E为AB中点,
∵四边形ABCD是菱形,
∴四边形DFEC是平行四边形.
(2)作 设 ,如图所示,
,
∵四边形ABCD是菱形,
在 中,
在 中, ( ,
即
整理得:
解得: (舍去),
9.(1)∵△ABC、△BEF是等边三角形,
∴BA=BC, BE=BF, ∠ABC=∠EBF=60°.
∴∠ABE=∠CBF,
∴△ABE≌△CBF(SAS),
∴CF = AE,
∵AE=1,
∴CF=1;
(2)连接CF, 如图所示:
∵△ABC、△BEF是等边三角形,
∴BA=BC, BE=BF, ∠ABC=∠EBF=60°,∠A =60°,
∴∠ABE=∠CBF,
∴△ABE≌△CBF(SAS),
∴CF = AE, ∠BCF =∠A =60°,
∵∠ABC = 60°,
∴∠BCF =∠ABC,
∴CF//AB,
∵△ABC是边长为3的等边三角形,
∴AC=3,
当点E在C处时, CF = AC,
当点E在A处时,点F与C重合,
∴点F运动的路径的长= AC =3;
(3)取BC中点H, 连接HN, 如图所示:
∵△ABC是等边三角形,
∴BC = AB = AC, ∠ABC = 60°,
∵CD⊥AB,
∴BH=BD,
∵△BMN是等边三角形,
∴BM = BN, ∠MBN =60°,
∴∠DBM =∠HBN,
∴△DBM≌△HBN(SAS),
∴HN=DM, ∠BHN =∠BDM =90°,
∴NH⊥BC,
∵△ABC是边长为3的等边三角形,
根据勾股定理,得
当点M在C处时,
当点M在D处时,点N与H重合,
∴点N所经过的路径的长
10.解:(1)∵ 四边形 ABCD 为矩形, 在 中,由勾股定理得: ∴AC的长为5;
(2)当( 时,如图1, 当 时,如图2,作 于H,
当 时,如图3,点 P与点C重合,
综上所述:
11.(1)证明: ∵△ABC是等腰直角三角形,
∴AB=AC,
∴∠B=∠ACB=45°,
∵CD⊥BC,
∴∠BCD = 90°,
∴∠ACD=∠BCD﹣∠ACB=45°=∠B,在△ABE和△ACD中,
∴△ABE≌△ACD(SAS);
(2)证明: 由 (1) 知,△ABE≌△ACD,
∴AE =AD, ∠BAE=∠CAD,
∵∠BAC =90°,
∴∠EAD=∠CAE+∠CAD=∠CAE+∠BAE=∠BAC=90°
,
∵∠EAF=45°,
∴∠DAF =∠DAE--∠EAF =45°=∠EAF,在△AEF与△ADF中,
∴△AEF≌△ADF(SAS),
∴DF=EF,
在Rt△DCF中,根据勾股定理得,
∵CD=BE,
(3)如图, 连接DE,
是等腰直角三角形,
∴当AE取最小值时,DE最小,此时.
∴DE的最小值为
12.(1) 证明: ∵PB'⊥AC, ∠CAB=90°,
∴∠B'PA=∠BAP,
又由折叠可知∠BAP =∠B'AP,
∴∠B'PA=∠B'AP.
故
(2)设AB= AC=a, AC、 PB'交于点D, 如答图1所示,则△ABC为等腰直角三角形,
由折叠可知,
∠PB'A=∠B=45°,
又∠ACB=45°,
∴∠PB'A=∠ACB,
又∠CDP=∠B'DA,
设 则
由得:
解得:
过点D作 于点E,则 为等腰直角三角形.
又
(3)存在点P, 使得 理由如下:
①如答图2所示,
由题意可知,点 的运动轨迹为以A为圆心、AB为半径的半圆A.
当P为BC中点时,
又
为等边三角形.
又由折叠可得四边形 为菱形.
又·
则易知AC为. '的垂直平分线.
故 满足题意.
此时,
②当点 落在BC上时,如答图3所示,此时 则
综上所述, 的值为 或
13.(1) ①过F作FG⊥BC于G, 连接CF, 如图:
∵四边形ABCD是正方形, ∠AEF =90°,
∴∠BAE=90°--∠AEB=∠FEG, ∠B=∠G=90°,
∵等腰直角三角形AEF,
∴AE = EF,
在△ABE和△EGF中,
∴△ABE≌△EGF(AAS),
∴EG﹣EC = BC﹣EC, 即
在Rt△CGF中,
②△ABE绕A逆时针旋转90°, 得△ADE', 过P作PH⊥EQ于H, 如图:
∵△ABE绕A逆时针旋转90°, 得△ADE',
∴△ABE≌△ADE',∠B =∠ADE'=90°,∠BAE=∠DAE', ∠AEB=∠E', AE=AE', BE=DE',
∴∠ADC+∠ADE'= 180°,
∴C、D、E'共线,
∵∠BAE+∠EAD=90°,
∴∠DAE'+∠EAD = 90°,
∵∠EAF =45°,
∴∠EAF =∠E'AF=45°,
在△EAQ和 中,
∴△EAQ≌△E'AQ(SAS),
∴∠E'=∠AEQ, EQ = E'Q,
∴∠AEB =∠AEQ, EQ=DQ+DE'=DQ+BE,
∴∠QEP=90°-∠AEQ =90°-∠AEB=∠CEP, 即EF是∠QEC的平分线,
又∠C =90°, PH⊥EQ,∴PH=PC,
∵∠BAE=∠CEP, ∠B=∠C =90°,
∴△ABE∽△ECP,
即
∴CP=m(1-m),
时,h最大值是
(2)①当 时,如图:
∵∠BAE=90°-∠AEB=∠HEG, ∠B=∠HGE=90°,
∴△ABE∽△EGH,
即
∵MG∥CD, G为BC中点,
∴MN为△ADQ的中位线,
由 (1) 知: EQ = DQ+BE,
设DQ=x, 则EQ=x+m, CQ=1-x,
中,
解得
②当 时,如图:
即
同①可得
(0≤m≤ 综上所述,
14.(1) 当 时,如图3中,点F与B重合.
由题意
故答案为:10,
(2)当( 时,重叠部分是
如图3中,在 中,
∴点P从A运动到C的时间
当5∵BL∥PF,
∴∠LBJ=∠PFE=45°,
∴△BLJ是等腰直角三角形,
∴LK=5 , AK=25,
∴BK = AB﹣AK =30﹣25=5,
∵BC∥KL,
∴∠FBT =∠BKL,
∴△FBT∽△BKL,
解法二:过点T作 于W, 求出TW, 根据 求解.
综上所述,
(3)当 时,
解得 或
不符合题意舍弃,
观察图象可知,满足条件的x的值为
15. (1) 设抛物线的表达式为 即 ,
即 解得
故抛物线的表达式为
(2)将点A的坐标代入直线l的表达式得:( 解得
故直线l的表达式为
设点Q的坐标为 则点P的坐标为
由题意得,点Q、M关于抛物线对称轴对称,而抛物线的对称轴为直线
故点M的横坐标为: 则 设矩形周长为C,则
故C有最小值,
当 时,矩形周长最小值为
(3)当 时, 即点Q的坐标为
由抛物线的表达式知,点D的坐标为
过点D作 于点K,
则
同理可得,
则
故
在 中,
故BF和BO重合,
故点F和点A重合,
即点F的坐标为(
【巩固练习1】
已知线段AB =12,CD =6,线段 CD 在直线AB上运动(点A 在 B,C 左侧,点 C 在点 D左侧).
(1)点M,N分别是线段AC,BD 的中点,若BC=4,求MN的长;
(2)当CD 运动到D 点与 B 点重合时,点P 是线段AB 延长线上一点,下列两个结论:是定值; 是定值,请作出正确的选择,并求出其定值.
【巩固练习2】
数轴上两个点A,B所对应的数为-8,7,M,N为数轴上的两点,表示的数分别为m,m+3.
(1)如图①,若AM = BN,直接写出 M,N点对应的数;
(2)若AN=2BM,求出m的值;
中小学教育资源及组卷应用平台
(3)若P 为AN的中点,点 Q 为 BM 的中点,问当m的值发生变化时,PQ 的值是否发生改变 如果不变,求出 PQ 的值;如果改变,说明理由.
【巩固练习3】
如图,C 为线段AB 上一点,且AC=2BC,AC 的 比BC小5.
(1)求AC,BC的长;
(2)点P从A点出发,以1个单位/秒的速度在线段AB 上向 B 点运动,设运动时间为 t秒(t<10),D 为PB的中点,E 为PC 的中点若 试求点 P 运动时间t的值;
(3)若P从A点出发,以1个单位/秒的速度在线段AB 上向 B 点运动,同时点 Q 从 B 点出发,以 个单位/秒的速度在 AB 的延长线上与P 点同向运动,运动时间t<30,D 为 PB的中点,F为DQ 的中点,E在PB 上且 PB,当P,Q两点运动的过程中,给出下面两个结论:①DE+DF 的值不变;②|DE-DF| 的值不变,其中只有一个结论是正确的,请判断正确的结论并求其值.
【巩固练习4】
如图,在射线OG上有三点A,B,C,满足OA=40 cm,AB=60 cm,BC=10 cm,点 P 从点O 出发,沿射线 OG 以 1 cm/s 的速度匀速运动,点Q 从点 C 出发沿射线 CO 匀速运动,其中点 P 和点 Q 两点同时出发,且P 运动到 B处时,P,Q停止运动.
(1)当P,Q 相遇时,有 PA=2PB,求点 Q的运动速度;
(2)若点 Q 的运动速度为3c m/s,则经过多长时间 P,Q两点相距70 cm;
(3)线段MN=10cm(N在M右侧),M与A 重合,线段 MN 从A 点出发,沿射线 AG 以2cm /s的速度匀速运动,若点 Q的运动速度为3c m/s,且P,Q,M,N同时运动,设运动时间为 ts,是否存在这样的t 值使得|MQ - PN| =2OP 若存在,求出t值;若不存在,说明理由.
【巩固练习5】
如图①,已知a,b满足( =0,c=2a+3b.且有理数a,b,c在数轴上对应的点分别为A,B,C.
(1)则a= ,b= ,c= ;
(2)点D 是数轴上A 点右侧一动点,点E,点F分别为CD,AD 中点,当点D 运动时,线段EF 的长度是否发生变化 若变化,请说明理由,若不变,请求出其值;
(3)若点A,B,C在数轴上运动,其中点 C以每秒1个单位的速度向左运动,同时点A 和点B 分别以每秒3 个单位和每秒2个单位的速度向右运动,请问:是否存在一个常数m使m·AB-2BC不随运动时间t的改变而改变 若存在,请求出m 和这个不变化的值;若不存在,请说明理由.
【巩固练习6】
点A 在数轴上对应的数为a,点B 对应的数为b,且a,b满足
(1)求线段AB 的长;
(2)点C 在数轴上对应的数为x,且x是方程 的根,在数轴上是否存在点 P,使得PA+PB=PC 若存在,直接写出点 P 对应的数;若不存在,说明理由;
(3)动点 P 从点A 出发,以每秒6个单位长度的速度沿数轴向左匀速运动;动点 Q 从点B出发,以每秒4个单位长度的速度沿数轴向左匀速移动;动点 M 从点 A 出发,以每秒3个单位长度的速度沿数轴向左匀速移动,设运动时间为t秒,当t<7时, 的值是否发生变化 若不变求出其值;若变化,写出范围.
【巩固练习7】
在矩形ABCD 中, 点E,F 分别是边AD、BC 上的动点,且AE =CF,连接EF,将矩形ABCD 沿 EF 折叠,点 C 落在点 G 处,点 D 落在点 H 处.
(1)如图①,当 EH 与线段 BC 交于点 P时,求证:PE=PF;
(2)如图②,当点 P 在线段 CB 的延长线上时,GH交AB 于点 M,求证:点 M 在线段EF的垂直平分线上;
(3)当AB=5 时,点 E 由点 A 移动到AD中点的过程中,计算出点 G运动的路线长.
【巩固练习8】
如图,在菱形 ABCD 中,∠DAB =60°,AB=2,点 E 为边 AB 上一个动点,延长 BA 到点F,使AF=AE,且CF、DE 相交于点 G.
(1)当点 E运动到AB中点时,证明:四边形DFEC 是平行四边形;
(2)当CG=2时,求AE的长;
(3)当点 E 从点 A 开始向右运动到点 B时,求点 G运动路径的长度.
【巩固练习9】
在数学兴趣小组活动中,小亮进行数学探究活动.
(1)△ABC 是边长为3 的等边三角形,E是边AC 上的一点,且AE=1,小亮以BE 为边作等边三角形BEF,如图①,求 CF 的长;
(2)△ABC 是边长为3 的等边三角形,E是边AC 上的一个动点,小亮以 BE 为边作等边三角形 BEF,如图②,在点 E 从点 C 到点 A的运动过程中,求点 F 所经过的路径长;
(3)△ABC 是边长为3的等边三角形,M是高 CD 上的一个动点,小亮以 BM 为边作等边三角形 BMN,如图③,在点 M 从点 C 到点 D的运动过程中,求点 N 所经过的路径长;
(4)正方形ABCD 的边长为3,E 是边 CB上的一个动点,在点E 从点 C 到点B 的运动过程中,小亮以 B 为顶点作正方形 BFGH,其中点 F、G都在直线AE 上,如图④,当点 E 到达点B时,点F、G、H与点B重合.则点H所经过的路径长为 ,点G所经过的路径长为
【巩固练习10】
如图,四边形ABCD 为矩形,AB=3,BC=4,P、Q 均从点B 出发,点 P 以2个单位每秒的速度沿 BA-AC 的方向运动,点 Q 以1个单位每秒的速度沿 BC-CD 运动,设运动时间为t秒.
(1)求AC 的长;
(2)若 求S关于t的解析式.
【巩固练习11】
如图①,E、F 是等腰 Rt△ABC 的斜边 BC上的两动点,∠EAF = 45°,CD ⊥BC 且 CD=BE.
(1)求证:△ABE≌△ACD;
(2)求证:
(3)如图②,作 AH⊥BC,垂足为 H,设∠EAH=α,∠FAH=β,不妨设 请利用(2)的结论证明:当α+β=45°时, tan(α+β) 成立.
【巩固练习12】
如图,在 Rt△ABC 中,点 P 为斜边 BC 上一动点,将△ABP 沿直线 AP 折叠,使得点 B 的对应点为B',连接AB',BB',PB'.
(1)如图①,若PB'⊥AC,证明:
(2)如图②,若 AB = AC,BP =3PC,求cos∠B'AC的值;
(3)如图③,若∠ACB=30°,是否存在点P,使得AB=CB'.若存在,求此时 的值;若不存在,请说明理由.
【巩固练习13】
已知四边形ABCD 是边长为1 的正方形,点 E 是射线BC 上的动点,以AE 为直角边在直线 BC 的上方作等腰直角三角形 AEF,∠AEF=90°,设BE=m.
(1)如图①,若点 E在线段BC 上运动,EF交 CD 于点 P,AF 交 CD 于点 Q,连接CF,
①当 时,求线段CF 的长;
②在△PQE'中,设边QE 上的高为h,请用含m的代数式表示h,并求h的最大值;
(2)设过BC 的中点且垂直于 BC 的直线被等腰直角三角形AEF 截得的线段长为y,请直接写出y与m的关系式.
【巩固练习14】
如图 ①,已 知 ∠RPQ = 45°, △ABC 中∠ACB=90°,动点 P 从点 A 出发,以: 的速度在线段AC 上向点 C 运动,PQ,PR分别与射线AB交于E,F两点,且PE⊥AB,当点 P与点 C 重合时停止运动,如图②,设点 P 的运动时间为 xs,∠RPQ 与△ABC 的重叠部分面积为ycm ,y与x的函数关系由 和 两段不同的图象组成.
(1)填空:①当x=5s时,EF= cm;②sinA = ;
(2)求y与x的函数关系式,并写出x的取值范围;
(3)当 时,请直接写出x的取值范围.
【巩固练习15】
如图①,抛物线 经过A(-1,0),B(4,0) 两点,与y 轴交于点 C,连接BC.
(1)求该抛物线的函数表达式;
(2)如图②,直线l :y= kx+3 经过点 A,点 P 为直线l上的一个动点,且位于x 轴的上方,点Q 为抛物线上的一个动点,当PQ//y轴时,作QM⊥PQ,交抛物线于点 M (点 M 在点Q 的右侧),以 PQ,QM 为邻边构造矩形PQMN,求该矩形周长的最小值;
(3)如图③,设抛物线的顶点为 D,在(2)的条件下,当矩形 PQMN 的周长取最小值时,抛物线上是否存在点 F,使得 若存在,请求出点 F 的坐标;若不存在,请说明理由.
1.(1)当点 C在点B 右侧时,如图(1),
∵M,N分别为线段AC,BD 的中点,
当点C在点 B 左侧时,如图(2),
∵M,N 分别为线段AC,BD 的中点,
综上所述,MN 的长为9.
(2)①正确, 理由如下:
是定值,定值为2.
而-8+6=-2,7--6=1,
∴M、N点对应的数分别是-2和1;
(2)∵A、B所对应的数分别是-8、7, M、N所对应的数分别是m、 m+3.
∴AN=|(m+3)-(-8)|=|m+11|, BM =|7-m|,
①当m≤–11时, 有m+11≤0, 7–m>0.
∴AN=|m+11|=-m--11, BM =|7-m|=7-m,由AN=2BM得, - m--11=2(7-m),
解得m=25,
∵m≤-11,
∴m=25不合题意, 舍去.
②当-11
∴AN=|m+11|=m+11, BM=|7-m|=7-m,由
AN =2BM得, m+11=2(7-m),解得m=1.
③当m>7时, 有m+11>0, 7-m<0.
∴AN=|m+11|=m+11, BM=|7-m|=m﹣7,
由AN=2BM得, m+11=2(m﹣7),
解得m=25,
综上所述: 当m=1或m=25时, AN =2BM.
(3)PQ的值不发生改变.
设P、Q表示的数为a、b.
∵点P为AN的中点,
①当点N在点A右侧时,点A,N表示的数分别为
解得
同理可得,
②当点N在点A左侧时,同理可得
∴PQ的值不发生改变,恒为6.
3.(1) 设 则
由题意得:
解得:
又∵D为PB的中点,.
∵ D为PB的中点, E为PC的中点,
又∵
解得:
(3)结论①正确, 值为: 理由如下:
设运动时间为t,
则
又∵F为DQ的中点,
4.(1)由题意可知, 若P在线段OA上, PA< PB, 不合题意舍去;
若P在线段AB上, PA+PB=60
∵PA=2PB
∴PB=20, OP=80
运动时间为t = 80s
∴点Q的运动速度为
故答案为:
(2)相遇前P, Q相距70cm, 得(1+3)t=110-70
∴t=10
相遇后P, Q相距70cm, 得(1+3)t=110+70
∴t=45
∴经过10s或45s, P, Q相距70cm;
故答案为: 10s或45s
(3)取O为数轴原点, 运动 ts后M对应的数为40﹢2t,N对应的数为50﹢2t, Q对应的数为110﹣3t, P对应的数为t,
∴MQ=|5t﹣70|, PN =50﹢t, OP=t
当MQ﹣PN=2OP时, 有|5t﹣70|﹣(50﹢t)=2t
∴t=60或
当PN﹣MQ=2OP时,有(50﹢t)﹣|5t﹣70|=2t
∴t=20或t=5
综上所述,存在这样的t,t值为 或5s或20s或60s
故答案为:t值为 或5s或20s或60s
5.(1)∵a、 b满足
∴a--2=0且 ab+6=0.
解得a=2, b=-3.
∴c=2a+3b=-5.
故答案为: 2, - 3, - 5
(2)如图, 当点 D 运动时, 线段
EF的长度不发生变化,理由如下:
∵点E.点 F分别为CD、 AD中点,
∴当点D 运动时,线段EF的长度不发生变化,其值为3.5;
(3)假设存在常数m使得m·AB--2BC 不随运动时间t的改变而改变。
则依题意得: AB=5+t, 2BC=4+6t.
所以m·AB﹣2BC=m(5﹢t)﹣(4﹢6t)=5m+ mt-4-6t 与t的值无关, 即m--6=0,
解得m=6,
6.(1) 由题意可知:
∴C对应的数为5,
当P在B左侧时,此时
故不满足题意,当P在AB之间时,此时
故不满足题意,
当P在A的右侧时,此时
故不满足题意,
故不存点P使得,
∴点P在点Q的右侧时,点Q、P、M三点在数轴上的位置依次从左向右,
则有:
7.(1)证明: 如图1中,
∵四边形ABCD是矩形,
由翻折变换可知,
(2)证明: 如图2中, 连接AC交EF于O, 连接PM, PO.
由折叠的性质可知ED=EH, 所以BF=EH,
∴PE﹣EH = PF﹣BF,
∴PB=PH,
∵∠PHM =∠PBM =90°, PM = PM,
∴Rt△PMH≌Rt△PMB(HL),
∴PM平分∠EPF,
∴点M在线段EF的垂直平分线上.
(3)如图3中,由题意,点E由点A移动到AD中点的过程中,点G运动的路径是图中弧BC.
在Rt△BCD中,
∴∠CBD=30°,
∴∠ABO=∠OAB =60°,
∴△AOB是等边三角形,
∴OA=OD=OB=OC=AB=5, ∠BOC=120°,
∴点G运动的路径的长
故答案为:
8.(1)证明: 连接DF, CE, 如图所示:
∵E为AB中点,
∵四边形ABCD是菱形,
∴四边形DFEC是平行四边形.
(2)作 设 ,如图所示,
,
∵四边形ABCD是菱形,
在 中,
在 中, ( ,
即
整理得:
解得: (舍去),
9.(1)∵△ABC、△BEF是等边三角形,
∴BA=BC, BE=BF, ∠ABC=∠EBF=60°.
∴∠ABE=∠CBF,
∴△ABE≌△CBF(SAS),
∴CF = AE,
∵AE=1,
∴CF=1;
(2)连接CF, 如图所示:
∵△ABC、△BEF是等边三角形,
∴BA=BC, BE=BF, ∠ABC=∠EBF=60°,∠A =60°,
∴∠ABE=∠CBF,
∴△ABE≌△CBF(SAS),
∴CF = AE, ∠BCF =∠A =60°,
∵∠ABC = 60°,
∴∠BCF =∠ABC,
∴CF//AB,
∵△ABC是边长为3的等边三角形,
∴AC=3,
当点E在C处时, CF = AC,
当点E在A处时,点F与C重合,
∴点F运动的路径的长= AC =3;
(3)取BC中点H, 连接HN, 如图所示:
∵△ABC是等边三角形,
∴BC = AB = AC, ∠ABC = 60°,
∵CD⊥AB,
∴BH=BD,
∵△BMN是等边三角形,
∴BM = BN, ∠MBN =60°,
∴∠DBM =∠HBN,
∴△DBM≌△HBN(SAS),
∴HN=DM, ∠BHN =∠BDM =90°,
∴NH⊥BC,
∵△ABC是边长为3的等边三角形,
根据勾股定理,得
当点M在C处时,
当点M在D处时,点N与H重合,
∴点N所经过的路径的长
10.解:(1)∵ 四边形 ABCD 为矩形, 在 中,由勾股定理得: ∴AC的长为5;
(2)当( 时,如图1, 当 时,如图2,作 于H,
当 时,如图3,点 P与点C重合,
综上所述:
11.(1)证明: ∵△ABC是等腰直角三角形,
∴AB=AC,
∴∠B=∠ACB=45°,
∵CD⊥BC,
∴∠BCD = 90°,
∴∠ACD=∠BCD﹣∠ACB=45°=∠B,在△ABE和△ACD中,
∴△ABE≌△ACD(SAS);
(2)证明: 由 (1) 知,△ABE≌△ACD,
∴AE =AD, ∠BAE=∠CAD,
∵∠BAC =90°,
∴∠EAD=∠CAE+∠CAD=∠CAE+∠BAE=∠BAC=90°
,
∵∠EAF=45°,
∴∠DAF =∠DAE--∠EAF =45°=∠EAF,在△AEF与△ADF中,
∴△AEF≌△ADF(SAS),
∴DF=EF,
在Rt△DCF中,根据勾股定理得,
∵CD=BE,
(3)如图, 连接DE,
是等腰直角三角形,
∴当AE取最小值时,DE最小,此时.
∴DE的最小值为
12.(1) 证明: ∵PB'⊥AC, ∠CAB=90°,
∴∠B'PA=∠BAP,
又由折叠可知∠BAP =∠B'AP,
∴∠B'PA=∠B'AP.
故
(2)设AB= AC=a, AC、 PB'交于点D, 如答图1所示,则△ABC为等腰直角三角形,
由折叠可知,
∠PB'A=∠B=45°,
又∠ACB=45°,
∴∠PB'A=∠ACB,
又∠CDP=∠B'DA,
设 则
由得:
解得:
过点D作 于点E,则 为等腰直角三角形.
又
(3)存在点P, 使得 理由如下:
①如答图2所示,
由题意可知,点 的运动轨迹为以A为圆心、AB为半径的半圆A.
当P为BC中点时,
又
为等边三角形.
又由折叠可得四边形 为菱形.
又·
则易知AC为. '的垂直平分线.
故 满足题意.
此时,
②当点 落在BC上时,如答图3所示,此时 则
综上所述, 的值为 或
13.(1) ①过F作FG⊥BC于G, 连接CF, 如图:
∵四边形ABCD是正方形, ∠AEF =90°,
∴∠BAE=90°--∠AEB=∠FEG, ∠B=∠G=90°,
∵等腰直角三角形AEF,
∴AE = EF,
在△ABE和△EGF中,
∴△ABE≌△EGF(AAS),
∴EG﹣EC = BC﹣EC, 即
在Rt△CGF中,
②△ABE绕A逆时针旋转90°, 得△ADE', 过P作PH⊥EQ于H, 如图:
∵△ABE绕A逆时针旋转90°, 得△ADE',
∴△ABE≌△ADE',∠B =∠ADE'=90°,∠BAE=∠DAE', ∠AEB=∠E', AE=AE', BE=DE',
∴∠ADC+∠ADE'= 180°,
∴C、D、E'共线,
∵∠BAE+∠EAD=90°,
∴∠DAE'+∠EAD = 90°,
∵∠EAF =45°,
∴∠EAF =∠E'AF=45°,
在△EAQ和 中,
∴△EAQ≌△E'AQ(SAS),
∴∠E'=∠AEQ, EQ = E'Q,
∴∠AEB =∠AEQ, EQ=DQ+DE'=DQ+BE,
∴∠QEP=90°-∠AEQ =90°-∠AEB=∠CEP, 即EF是∠QEC的平分线,
又∠C =90°, PH⊥EQ,∴PH=PC,
∵∠BAE=∠CEP, ∠B=∠C =90°,
∴△ABE∽△ECP,
即
∴CP=m(1-m),
时,h最大值是
(2)①当 时,如图:
∵∠BAE=90°-∠AEB=∠HEG, ∠B=∠HGE=90°,
∴△ABE∽△EGH,
即
∵MG∥CD, G为BC中点,
∴MN为△ADQ的中位线,
由 (1) 知: EQ = DQ+BE,
设DQ=x, 则EQ=x+m, CQ=1-x,
中,
解得
②当 时,如图:
即
同①可得
(0≤m≤ 综上所述,
14.(1) 当 时,如图3中,点F与B重合.
由题意
故答案为:10,
(2)当( 时,重叠部分是
如图3中,在 中,
∴点P从A运动到C的时间
当5
∴∠LBJ=∠PFE=45°,
∴△BLJ是等腰直角三角形,
∴LK=5 , AK=25,
∴BK = AB﹣AK =30﹣25=5,
∵BC∥KL,
∴∠FBT =∠BKL,
∴△FBT∽△BKL,
解法二:过点T作 于W, 求出TW, 根据 求解.
综上所述,
(3)当 时,
解得 或
不符合题意舍弃,
观察图象可知,满足条件的x的值为
15. (1) 设抛物线的表达式为 即 ,
即 解得
故抛物线的表达式为
(2)将点A的坐标代入直线l的表达式得:( 解得
故直线l的表达式为
设点Q的坐标为 则点P的坐标为
由题意得,点Q、M关于抛物线对称轴对称,而抛物线的对称轴为直线
故点M的横坐标为: 则 设矩形周长为C,则
故C有最小值,
当 时,矩形周长最小值为
(3)当 时, 即点Q的坐标为
由抛物线的表达式知,点D的坐标为
过点D作 于点K,
则
同理可得,
则
故
在 中,
故BF和BO重合,
故点F和点A重合,
即点F的坐标为(
同课章节目录
