2025年中考数学复习--角度的动态问题 方法讲解及巩固练习(含解析)
文档属性
| 名称 | 2025年中考数学复习--角度的动态问题 方法讲解及巩固练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 378.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 00:00:00 | ||
图片预览



文档简介
角度的动态问题
类型一:钟表问题
【方法技巧】
(1)整个钟面为360°,有12个大格,每个大格为30°;60个小格,每个小格为6°;
(2)整个分针速度:每分钟走一小格,每分钟走6°,1小时转360°;
(3)时针速度:每分钟走 小格,每分钟走0.5°,1 小时转30°.
方法一:画图计算.
方法二:列方程求解.
注意:相邻两次重合之间,一次平角,两次直角.
典例精析
【典型题1】★★10 点20 分,钟表上时针与分针所成的钝角是 °.
【思路分析】整个钟面为360°,有12个大格,每个大格为30°,时针每分钟走0.5°.
【答案解析】解:10 点20分,钟表上分针在数字4 上,时针从数字10 开始,走了20 个0.5°.因此这时候钟表上时针与分针所成的钝角是30×6+0.5×20=190°.
【典型题2】★★某时刻,钟表上的时针和分针所成的夹角是105°,那么这一时刻可能是( )
A.8点30分 B.9点30分
C.10点30分 D.1点30分
【答案解析】解:当时间是9 点30 分时,分针在数字6的位置,而时针在9 和10 的正中间,所以时针和分针所成的夹角等于90°+15°=105°.选择 B.
【典型题3】
(1)小明出门吃饭时时间为10点多,时针刚好和分针重合,回来时2 点多,时针与分针又刚好重合,出门时间和回家时间分别为几点几分
(2)4点到5点之间,时针和分针成直角的时间为 .
【思路分析】(1)10点整到10点多重合:
类型二:角度的旋转
【方法技巧】解题三大步骤:
(1)设未知数,表示所有小角.
(2)固定图形,寻找角度关系,建立关系式.
(3)求解.
典例精析
【典型题1】★★ 如图,∠AOB 为直角,分针从指针12 开始,到超过指针10,时针从指针10 开始,到超过指针10 最后和分针重合.整个过程,分针比时针多转指针12 - 10,共300°.2点整到2点多则分针比时针多转60°.列方程求解.分针每分钟走一小格,每分钟走6°,时针每分钟走0.5°.
(2)需要注意分针和时针的前后顺序,所以需分类讨论.时针在分针前面时,类似(1),4点整到4点多,分针比时针多转(120°-90°),时针在分针前面时,分针比时针多转(120°+90°).
【答案解析】解:
(1)设出门的时间为10点x分,回家的时间是2点y分.
则由题意得,6x-0.5x=300,解得x =54 ,6y-0.5y=60,解得 出门时间为10点54 分,回家时间为2点1 分.
(2)设时间为4点x分,
①时针在分针前面时,由题意得,6x -0.5x=120-90,解得
②时针在分针后面时,由题意得,6x-0.5x=120+90,解得
∴在4点5 分或者4点38 分时,时针与分针成直角.
∠AOC 为锐角,且 OM 平分∠BOC,ON 平分∠AOC.
如果∠AOC=50°,求∠MON的度数.
(2)如果∠AOC 为任意一个锐角,能求出∠MON的度数吗 若能,请求出来,若不能,请说明理由.
【思路分析】设未知数,表示小角.设∠AOM=x.
【答案解析】解:(1)45°;
(2)能,设∠AOM=x,则∠BOM=90°-x,∠COM=∠BOM=90°-x,
∴ ∠MON=∠AOM+∠AON=45°.
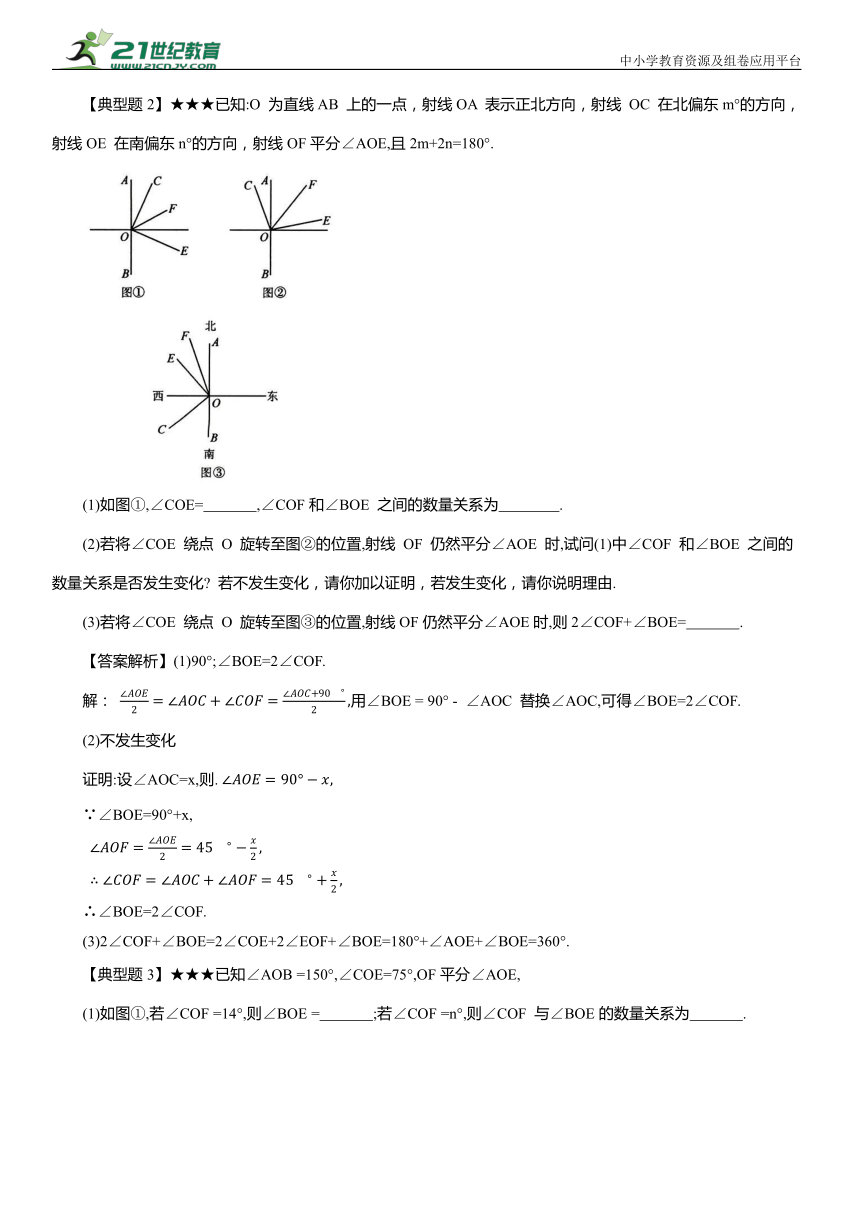
【典型题2】★★★已知:O 为直线AB 上的一点,射线OA 表示正北方向,射线 OC 在北偏东m°的方向,射线OE 在南偏东n°的方向,射线OF平分∠AOE,且2m+2n=180°.
(1)如图①,∠COE= ,∠COF和∠BOE 之间的数量关系为 .
(2)若将∠COE 绕点 O 旋转至图②的位置,射线 OF 仍然平分∠AOE 时,试问(1)中∠COF 和∠BOE 之间的数量关系是否发生变化 若不发生变化,请你加以证明,若发生变化,请你说明理由.
(3)若将∠COE 绕点 O 旋转至图③的位置,射线OF仍然平分∠AOE时,则2∠COF+∠BOE= .
【答案解析】(1)90°;∠BOE=2∠COF.
解: 用∠BOE = 90° - ∠AOC 替换∠AOC,可得∠BOE=2∠COF.
(2)不发生变化
证明:设∠AOC=x,则.
∵∠BOE=90°+x,
∴∠BOE=2∠COF.
(3)2∠COF+∠BOE=2∠COE+2∠EOF+∠BOE=180°+∠AOE+∠BOE=360°.
【典型题3】★★★已知∠AOB =150°,∠COE=75°,OF平分∠AOE,
(1)如图①,若∠COF =14°,则∠BOE = ;若∠COF =n°,则∠COF 与∠BOE的数量关系为 .
当射线 OE 绕点 O 逆时针旋转到如图②的位置时,(1)中∠BOE 与∠COF 的数量关系是否仍然成立 请说明理由.
(3)在(2)的条件下,如图③,在∠BOE的内部是否存在一条射线 OD,使得∠BOD 为直角,且∠DOF =3 ∠DOE. 若存在,请求出∠COF的度数;若不存在,请说明理由.
【答案解析】(1)28°,∠BOE=2∠COF.
解: 用∠BOE =75° - ∠AOC 替换∠AOC,可得∠BOE=2∠COF.
(2)仍然成立,设∠AOF为x,则∠EOF=∠AOF =x,∴∠COF =75°-x,∠BOE =150°-2x,∴∠BOE=2∠COF,
(3) 设 ∠DOE = x, 则 由题 ∠DOF =3∠DOE=3x,
∴∠EOF =2x,∠AOF =2x,∠AOD =5x,∠COF=75°-2x
由题意得,5x+90°=150°,解得 x =12°,∴∠COF=51°
【典型题4】如图①,射线OC、OD在∠AOB 的内部,且∠AOB =150°,∠COD =30°,射线OM、ON分别平分∠AOD、∠BOC,
(1)设∠NOD 为x,∠COM 为y,完成下表,并求∠MON的大小,并说明理由.
角 ∠NOC ∠DOM ∠BON ∠AOM ∠MON
度数
(2)如图②,若∠AOC =15°,将∠COD 绕点O 以每秒m°的速度逆时针旋转10s,此时∠AOM: ∠BON =7:11,如图③所示,求 m的值.
【答案解析】解:(1)x+30°,y+30°,x+30°,y+30°,x+y+30°
由题意得,2x+2y+90°=150°,解得x+y=30°,∴∠MON=x+y+30°=60°.
(2)由题意得,
解得m=2.5.
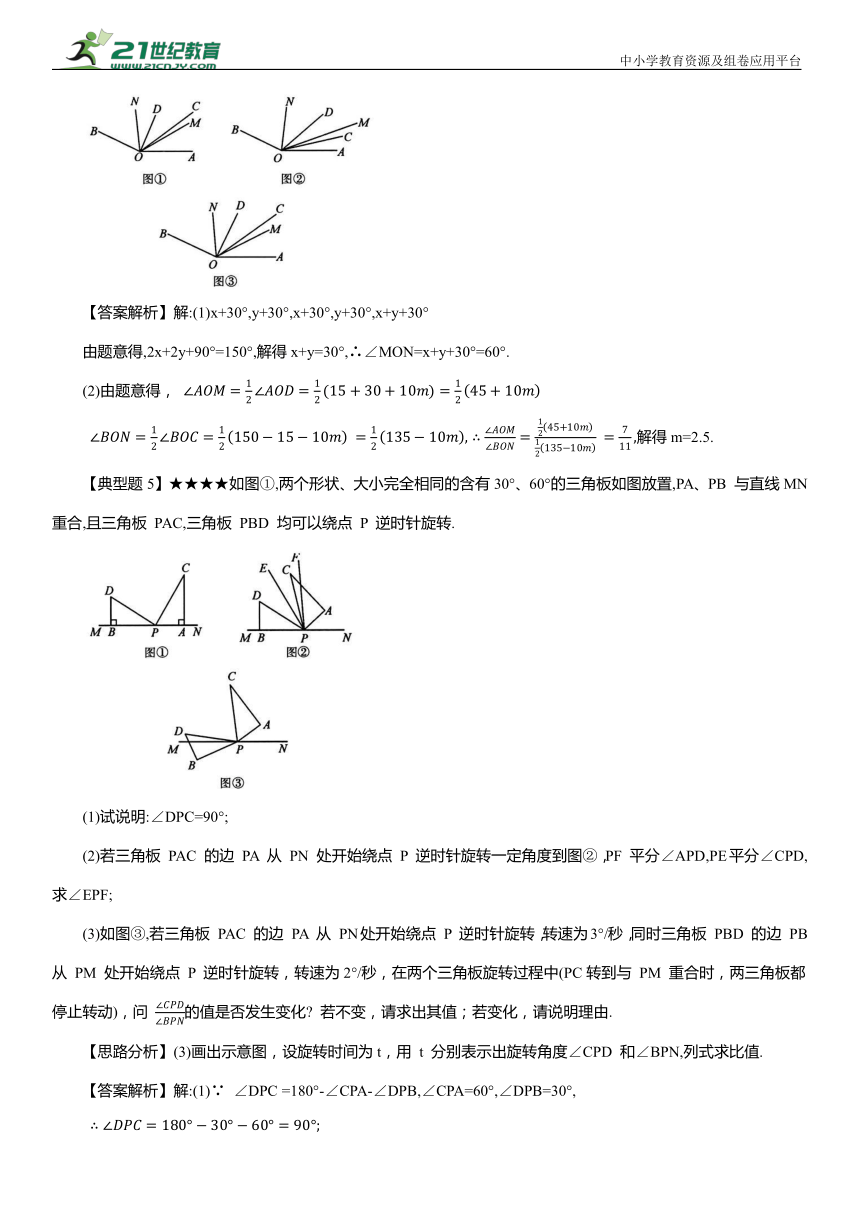
【典型题5】★★★★如图①,两个形状、大小完全相同的含有30°、60°的三角板如图放置,PA、PB 与直线MN 重合,且三角板 PAC,三角板 PBD 均可以绕点 P 逆时针旋转.
(1)试说明:∠DPC=90°;
(2)若三角板 PAC 的边 PA 从 PN 处开始绕点 P 逆时针旋转一定角度到图②,PF 平分∠APD,PE平分∠CPD,求∠EPF;
(3)如图③,若三角板 PAC 的边 PA 从 PN处开始绕点 P 逆时针旋转,转速为3°/秒,同时三角板 PBD 的边 PB 从 PM 处开始绕点 P 逆时针旋转,转速为2°/秒,在两个三角板旋转过程中(PC转到与 PM 重合时,两三角板都停止转动),问 的值是否发生变化 若不变,请求出其值;若变化,请说明理由.
【思路分析】(3)画出示意图,设旋转时间为t,用 t 分别表示出旋转角度∠CPD 和∠BPN,列式求比值.
【答案解析】解:(1)∵ ∠DPC =180°-∠CPA-∠DPB,∠CPA=60°,∠DPB=30°,
(2)设∠CPE=∠DPE=x,∠CPF =y,则∠APF=∠DPF=2x+y,
∵∠CPA=60°,∴y+2x+y=60°,∴x +y=30°,∴∠EPF =x+y=30°.
的值是定值. 设运动时间为t秒,∵∠BPM =2t,∴∠BPN =180°-2t,∵ PC和 PD 的旋转速度差为t,∴∠CPD=90°-t.
如图,且PD转到在 PM 上方和下方时均成立.
的值是定值
巩固练习
【巩固练习1】
O 为直线 AD 上一点,以O 为顶点作∠COE=90°,射线OF 平分∠AOE.
(1)如图①,∠AOC 与∠DOE 的数量关系为 ,∠COF 和∠DOE 的数量关系为 ;
(2)若将∠COE 绕点 O 旋转至图②的位置,OF 依然平分∠AOE,请写出∠COF 和∠DOE之间的数量关系,并说明理由;
(3)若将∠COE 绕点 O 旋转至图③的位置,射线 OF 依然平分∠AOE,请直接写出∠COF 和∠DOE 之间的数量关系.
【巩固练习2】
已知∠AOB=100°,∠COD=40°,OE平分∠AOC,OF 平分∠BOD.(本题中的角均为大于0°且小于等于180°的角).
(1)如图所示,当 OB、OC 重合时,求∠EOF 的度数;
(2)当∠COD 从图中所示位置绕点 O 顺时针旋转n°(0(3)当∠COD 从图中所示位置绕点 O 顺时针旋转 时,满足∠AOD +∠EOF=6∠COD,则n= .
【巩固练习3】
如图①,点 O 为直线AB 上一点,过点 O作射线OC,使 将一直角三角板的直角顶点放在点 O 处( 一边OM 在射线 OB 上,另一边 ON 在直线 AB 的下方.
(1)将图①中的三角板绕点 O 逆时针旋转至图②,使一边 OM 在∠BOC 的内部,且恰好平分∠BOC.求∠BON的度数.
(2)将图①中的三角板绕点 O 以每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t 秒时,直线 ON恰好平分锐角∠AOC,则t的值为 (直接写出结果).
(3)将图①中的三角板绕点 O 顺时针旋转至图③,使 ON 在∠AOC 的内部,请探究∠AOM 与∠NOC 的数量关系,并说明理由.
【巩固练习4】
将一副三角板中的两块直角三角尺的直角顶点 O 按如图方式叠放在一起.
(1)如图①若∠BOD=35°,求∠AOC 的度数,若∠AOC=135°,求∠BOD 的度数.
(2)如图②若∠AOC =150°,求∠BOD 的度数.
(3)猜想∠AOC 与∠BOD 的数量关系,并结合图①说明理由.
(4)三角尺 AOB 不动,将三角尺 COD 的OD 边与OA 边重合,然后绕点 O 按顺时针或逆时针方向任意转动一个角度,当 )等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD 所有可能的值,不用说明理由.
1.
∵射线OF平分
∵O为直线AD上一点,
∵射线OF平分.
2.(1)∵OE平分∠AOC, OF平分∠BOD,
∴∠EOF =∠EOC+∠COF =50°+20°=70°;
(2)∠AOE--∠BOF的值为定值, 理由如下:根据题意知∠BOC =n°.
.
∵OE平分∠AOC, OF平分∠BOD,
;
(3)当0'∠EOF =∠EOC+∠COF =∠EOC+∠COD﹣∠DOF =
,
∵∠AOD+∠EOF =6∠COD,
∴(140+n)+70°=6×40,
∴n=30.
故答案为: 30.
3.
如图2,
∵OM平分.
又·.·
11或47
【解析】
中小学教育资源及组卷应用平台
分两种情况:
①如图2,
∵∠BOC=110°,
∴∠AOC =70°,
当直线ON恰好平分锐角∠AOC时, ∠AOD=∠COD=35°,
∴∠BON =35°, ∠BOM = 55°,
即逆时针旋转的角度为55°,
由题意得, 5t=55°,
解得t =11(s);
②如图3, 当ON平分∠AOC时, ∠NOA =35°,
∴∠AOM =55°,
即逆时针旋转的角度为:180°+55°= 235°,
由题意得, 5t= 235°,
解得t=47(s),
综上所述, t=11s或47s时, 直线ON恰好平分锐角∠AOC。
故答案为: 11或47。
4.∠AOM﹣∠NOC=20°。
理由: ∵∠MON =70°, ∠AOC =70°,
∴∠AOM =90°--∠AON, ∠NOC =70°--∠AON,
∴∠AOM﹣∠NOC =(90°﹣∠AON)﹣(70°﹣∠AON)=20°
∴∠AOM与∠NOC的数量关系为: ∠AOM--∠NOC =20°
5.【答案】
(1)若∠BOD =35°, 则∠AOC =145°; 若∠AOC=35°, 则∠BOD=45°
(2)∠BOD=30°
(3)∠AOC+∠BOD =180°, 理由见解析
【解析】
(1)当∠BOD =35°时
∠AOC =∠AOB+∠COD--∠BOD
=90°+90°-35°
= 145°
当∠AOC =135°时
∠BOD =∠AOB+∠COD-∠AOC
=90°+90°--135°
= 45°
(2)已知: ∠AOC+∠COD+∠BOD+∠AOB=360°
又知: ∠AOB=∠COD=90°, ∠AOC =150°
∴150°+90°+∠BOD+90°=360°
∴∠BOD=30°
(3)∠AOC+∠BOD =180°, 理由如下:
∵∠AOB=∠COD=90°
∴∠AOD+∠BOD+∠BOD+∠BOC =180°
又知: ∠AOD+∠BOD+∠BOC =∠AOC
∴∠AOC+∠BOD =180°
类型一:钟表问题
【方法技巧】
(1)整个钟面为360°,有12个大格,每个大格为30°;60个小格,每个小格为6°;
(2)整个分针速度:每分钟走一小格,每分钟走6°,1小时转360°;
(3)时针速度:每分钟走 小格,每分钟走0.5°,1 小时转30°.
方法一:画图计算.
方法二:列方程求解.
注意:相邻两次重合之间,一次平角,两次直角.
典例精析
【典型题1】★★10 点20 分,钟表上时针与分针所成的钝角是 °.
【思路分析】整个钟面为360°,有12个大格,每个大格为30°,时针每分钟走0.5°.
【答案解析】解:10 点20分,钟表上分针在数字4 上,时针从数字10 开始,走了20 个0.5°.因此这时候钟表上时针与分针所成的钝角是30×6+0.5×20=190°.
【典型题2】★★某时刻,钟表上的时针和分针所成的夹角是105°,那么这一时刻可能是( )
A.8点30分 B.9点30分
C.10点30分 D.1点30分
【答案解析】解:当时间是9 点30 分时,分针在数字6的位置,而时针在9 和10 的正中间,所以时针和分针所成的夹角等于90°+15°=105°.选择 B.
【典型题3】
(1)小明出门吃饭时时间为10点多,时针刚好和分针重合,回来时2 点多,时针与分针又刚好重合,出门时间和回家时间分别为几点几分
(2)4点到5点之间,时针和分针成直角的时间为 .
【思路分析】(1)10点整到10点多重合:
类型二:角度的旋转
【方法技巧】解题三大步骤:
(1)设未知数,表示所有小角.
(2)固定图形,寻找角度关系,建立关系式.
(3)求解.
典例精析
【典型题1】★★ 如图,∠AOB 为直角,分针从指针12 开始,到超过指针10,时针从指针10 开始,到超过指针10 最后和分针重合.整个过程,分针比时针多转指针12 - 10,共300°.2点整到2点多则分针比时针多转60°.列方程求解.分针每分钟走一小格,每分钟走6°,时针每分钟走0.5°.
(2)需要注意分针和时针的前后顺序,所以需分类讨论.时针在分针前面时,类似(1),4点整到4点多,分针比时针多转(120°-90°),时针在分针前面时,分针比时针多转(120°+90°).
【答案解析】解:
(1)设出门的时间为10点x分,回家的时间是2点y分.
则由题意得,6x-0.5x=300,解得x =54 ,6y-0.5y=60,解得 出门时间为10点54 分,回家时间为2点1 分.
(2)设时间为4点x分,
①时针在分针前面时,由题意得,6x -0.5x=120-90,解得
②时针在分针后面时,由题意得,6x-0.5x=120+90,解得
∴在4点5 分或者4点38 分时,时针与分针成直角.
∠AOC 为锐角,且 OM 平分∠BOC,ON 平分∠AOC.
如果∠AOC=50°,求∠MON的度数.
(2)如果∠AOC 为任意一个锐角,能求出∠MON的度数吗 若能,请求出来,若不能,请说明理由.
【思路分析】设未知数,表示小角.设∠AOM=x.
【答案解析】解:(1)45°;
(2)能,设∠AOM=x,则∠BOM=90°-x,∠COM=∠BOM=90°-x,
∴ ∠MON=∠AOM+∠AON=45°.
【典型题2】★★★已知:O 为直线AB 上的一点,射线OA 表示正北方向,射线 OC 在北偏东m°的方向,射线OE 在南偏东n°的方向,射线OF平分∠AOE,且2m+2n=180°.
(1)如图①,∠COE= ,∠COF和∠BOE 之间的数量关系为 .
(2)若将∠COE 绕点 O 旋转至图②的位置,射线 OF 仍然平分∠AOE 时,试问(1)中∠COF 和∠BOE 之间的数量关系是否发生变化 若不发生变化,请你加以证明,若发生变化,请你说明理由.
(3)若将∠COE 绕点 O 旋转至图③的位置,射线OF仍然平分∠AOE时,则2∠COF+∠BOE= .
【答案解析】(1)90°;∠BOE=2∠COF.
解: 用∠BOE = 90° - ∠AOC 替换∠AOC,可得∠BOE=2∠COF.
(2)不发生变化
证明:设∠AOC=x,则.
∵∠BOE=90°+x,
∴∠BOE=2∠COF.
(3)2∠COF+∠BOE=2∠COE+2∠EOF+∠BOE=180°+∠AOE+∠BOE=360°.
【典型题3】★★★已知∠AOB =150°,∠COE=75°,OF平分∠AOE,
(1)如图①,若∠COF =14°,则∠BOE = ;若∠COF =n°,则∠COF 与∠BOE的数量关系为 .
当射线 OE 绕点 O 逆时针旋转到如图②的位置时,(1)中∠BOE 与∠COF 的数量关系是否仍然成立 请说明理由.
(3)在(2)的条件下,如图③,在∠BOE的内部是否存在一条射线 OD,使得∠BOD 为直角,且∠DOF =3 ∠DOE. 若存在,请求出∠COF的度数;若不存在,请说明理由.
【答案解析】(1)28°,∠BOE=2∠COF.
解: 用∠BOE =75° - ∠AOC 替换∠AOC,可得∠BOE=2∠COF.
(2)仍然成立,设∠AOF为x,则∠EOF=∠AOF =x,∴∠COF =75°-x,∠BOE =150°-2x,∴∠BOE=2∠COF,
(3) 设 ∠DOE = x, 则 由题 ∠DOF =3∠DOE=3x,
∴∠EOF =2x,∠AOF =2x,∠AOD =5x,∠COF=75°-2x
由题意得,5x+90°=150°,解得 x =12°,∴∠COF=51°
【典型题4】如图①,射线OC、OD在∠AOB 的内部,且∠AOB =150°,∠COD =30°,射线OM、ON分别平分∠AOD、∠BOC,
(1)设∠NOD 为x,∠COM 为y,完成下表,并求∠MON的大小,并说明理由.
角 ∠NOC ∠DOM ∠BON ∠AOM ∠MON
度数
(2)如图②,若∠AOC =15°,将∠COD 绕点O 以每秒m°的速度逆时针旋转10s,此时∠AOM: ∠BON =7:11,如图③所示,求 m的值.
【答案解析】解:(1)x+30°,y+30°,x+30°,y+30°,x+y+30°
由题意得,2x+2y+90°=150°,解得x+y=30°,∴∠MON=x+y+30°=60°.
(2)由题意得,
解得m=2.5.
【典型题5】★★★★如图①,两个形状、大小完全相同的含有30°、60°的三角板如图放置,PA、PB 与直线MN 重合,且三角板 PAC,三角板 PBD 均可以绕点 P 逆时针旋转.
(1)试说明:∠DPC=90°;
(2)若三角板 PAC 的边 PA 从 PN 处开始绕点 P 逆时针旋转一定角度到图②,PF 平分∠APD,PE平分∠CPD,求∠EPF;
(3)如图③,若三角板 PAC 的边 PA 从 PN处开始绕点 P 逆时针旋转,转速为3°/秒,同时三角板 PBD 的边 PB 从 PM 处开始绕点 P 逆时针旋转,转速为2°/秒,在两个三角板旋转过程中(PC转到与 PM 重合时,两三角板都停止转动),问 的值是否发生变化 若不变,请求出其值;若变化,请说明理由.
【思路分析】(3)画出示意图,设旋转时间为t,用 t 分别表示出旋转角度∠CPD 和∠BPN,列式求比值.
【答案解析】解:(1)∵ ∠DPC =180°-∠CPA-∠DPB,∠CPA=60°,∠DPB=30°,
(2)设∠CPE=∠DPE=x,∠CPF =y,则∠APF=∠DPF=2x+y,
∵∠CPA=60°,∴y+2x+y=60°,∴x +y=30°,∴∠EPF =x+y=30°.
的值是定值. 设运动时间为t秒,∵∠BPM =2t,∴∠BPN =180°-2t,∵ PC和 PD 的旋转速度差为t,∴∠CPD=90°-t.
如图,且PD转到在 PM 上方和下方时均成立.
的值是定值
巩固练习
【巩固练习1】
O 为直线 AD 上一点,以O 为顶点作∠COE=90°,射线OF 平分∠AOE.
(1)如图①,∠AOC 与∠DOE 的数量关系为 ,∠COF 和∠DOE 的数量关系为 ;
(2)若将∠COE 绕点 O 旋转至图②的位置,OF 依然平分∠AOE,请写出∠COF 和∠DOE之间的数量关系,并说明理由;
(3)若将∠COE 绕点 O 旋转至图③的位置,射线 OF 依然平分∠AOE,请直接写出∠COF 和∠DOE 之间的数量关系.
【巩固练习2】
已知∠AOB=100°,∠COD=40°,OE平分∠AOC,OF 平分∠BOD.(本题中的角均为大于0°且小于等于180°的角).
(1)如图所示,当 OB、OC 重合时,求∠EOF 的度数;
(2)当∠COD 从图中所示位置绕点 O 顺时针旋转n°(0
【巩固练习3】
如图①,点 O 为直线AB 上一点,过点 O作射线OC,使 将一直角三角板的直角顶点放在点 O 处( 一边OM 在射线 OB 上,另一边 ON 在直线 AB 的下方.
(1)将图①中的三角板绕点 O 逆时针旋转至图②,使一边 OM 在∠BOC 的内部,且恰好平分∠BOC.求∠BON的度数.
(2)将图①中的三角板绕点 O 以每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t 秒时,直线 ON恰好平分锐角∠AOC,则t的值为 (直接写出结果).
(3)将图①中的三角板绕点 O 顺时针旋转至图③,使 ON 在∠AOC 的内部,请探究∠AOM 与∠NOC 的数量关系,并说明理由.
【巩固练习4】
将一副三角板中的两块直角三角尺的直角顶点 O 按如图方式叠放在一起.
(1)如图①若∠BOD=35°,求∠AOC 的度数,若∠AOC=135°,求∠BOD 的度数.
(2)如图②若∠AOC =150°,求∠BOD 的度数.
(3)猜想∠AOC 与∠BOD 的数量关系,并结合图①说明理由.
(4)三角尺 AOB 不动,将三角尺 COD 的OD 边与OA 边重合,然后绕点 O 按顺时针或逆时针方向任意转动一个角度,当 )等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD 所有可能的值,不用说明理由.
1.
∵射线OF平分
∵O为直线AD上一点,
∵射线OF平分.
2.(1)∵OE平分∠AOC, OF平分∠BOD,
∴∠EOF =∠EOC+∠COF =50°+20°=70°;
(2)∠AOE--∠BOF的值为定值, 理由如下:根据题意知∠BOC =n°.
.
∵OE平分∠AOC, OF平分∠BOD,
;
(3)当0
,
∵∠AOD+∠EOF =6∠COD,
∴(140+n)+70°=6×40,
∴n=30.
故答案为: 30.
3.
如图2,
∵OM平分.
又·.·
11或47
【解析】
中小学教育资源及组卷应用平台
分两种情况:
①如图2,
∵∠BOC=110°,
∴∠AOC =70°,
当直线ON恰好平分锐角∠AOC时, ∠AOD=∠COD=35°,
∴∠BON =35°, ∠BOM = 55°,
即逆时针旋转的角度为55°,
由题意得, 5t=55°,
解得t =11(s);
②如图3, 当ON平分∠AOC时, ∠NOA =35°,
∴∠AOM =55°,
即逆时针旋转的角度为:180°+55°= 235°,
由题意得, 5t= 235°,
解得t=47(s),
综上所述, t=11s或47s时, 直线ON恰好平分锐角∠AOC。
故答案为: 11或47。
4.∠AOM﹣∠NOC=20°。
理由: ∵∠MON =70°, ∠AOC =70°,
∴∠AOM =90°--∠AON, ∠NOC =70°--∠AON,
∴∠AOM﹣∠NOC =(90°﹣∠AON)﹣(70°﹣∠AON)=20°
∴∠AOM与∠NOC的数量关系为: ∠AOM--∠NOC =20°
5.【答案】
(1)若∠BOD =35°, 则∠AOC =145°; 若∠AOC=35°, 则∠BOD=45°
(2)∠BOD=30°
(3)∠AOC+∠BOD =180°, 理由见解析
【解析】
(1)当∠BOD =35°时
∠AOC =∠AOB+∠COD--∠BOD
=90°+90°-35°
= 145°
当∠AOC =135°时
∠BOD =∠AOB+∠COD-∠AOC
=90°+90°--135°
= 45°
(2)已知: ∠AOC+∠COD+∠BOD+∠AOB=360°
又知: ∠AOB=∠COD=90°, ∠AOC =150°
∴150°+90°+∠BOD+90°=360°
∴∠BOD=30°
(3)∠AOC+∠BOD =180°, 理由如下:
∵∠AOB=∠COD=90°
∴∠AOD+∠BOD+∠BOD+∠BOC =180°
又知: ∠AOD+∠BOD+∠BOC =∠AOC
∴∠AOC+∠BOD =180°
同课章节目录
