2025年中考数学复习---垂线相关的辅助线 方法讲解及巩固练习(含解析)
文档属性
| 名称 | 2025年中考数学复习---垂线相关的辅助线 方法讲解及巩固练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 677.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 06:27:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
垂线相关的辅助线
典例精析
【典型题1】★· 如图所示,△ABC 中,AB=AC,∠BAC =120°,AC 的垂直平分线 EF 交AC 于点E,交 BC 于点 F.求证:BF=2CF.
【思路分析】思路一(正向推导法):从题目条件分析,EF 是AC 的垂直平分线,因此连接AF,可得AF=FC,即将要证明BF=2CF转化为证明BF =2AF,再由已知角度容易得出∠B=30°,∠BAF=90°,可得BF=2AF.
思路二(逆向分析法):从结论出发分析,要证明BF=2CF,自然想到应用“直角三角形30°角所对的直角边等于斜边的一半”这条性质,再从题目条件“AB=AC,∠BAC=120°”求出∠B = ∠C = 30°,从而连接 AF 构造Rt△BAF,又根据中垂线定理可得AF =CF,问题得证.
【答案解析】解:连接AF,
∵AB=AC ,∴∠B=∠C;
又∵∠BAC=120°,∴∠B+∠C=60°
∴∠B=∠C=30°,
∵ EF 垂直平分AC∴ FA =FC,
∴∠FAC=∠C=30°,
又∵∠BAC=120°,
∵∠B=30°∴BF=2AF,
∵FA=FC ∴BF=2CF.
【规律总结】辅助线作法:方法①:垂直平分连两端.方法②:构造特殊三角形.
【典型题2】★★★如图,在△ABC中,∠B=45°,AB=6 ,D、E分别是AB、AC的中点,连接DE,在直线DE 和直线BC 上分别取点F、G,连接BF、DG.若BF=3DG,且直线BF与直线DG互相垂直,则BG的长为 .
【思路分析】本题比较难,需从题目条件入手分析,正向推导,作垂线构造直角三角形.注意需分点 F 在点 D 的两侧分类讨论.
注:本题同学们也可尝试其他方法,比如过点 F 作BF的垂线(或者DG的平行线,道理相同,目的是构造直角三角形).
【答案解析】解:如图,当点 F 在点 D 的右侧时,过点 B 作 BT⊥BF 交 ED的延长线于T,过点 B 作 BH⊥DT于 H.
∵DG⊥BF,BT⊥BF,∴DG//BT,
∵AD=DB,AE=EC,∴DE//BC,
∴四边形DGBT是平行四边形,
∴BG=DT,DG=BT,
∠BDH=∠ABC=45°,
∵∠TBF=∠BHF=90°,
∴∠TBH+∠FBH=90°,
∵∠FBH+∠F=90°,
∴∠TBH=∠F,
∴TH=1,∴DT=TH+DH=1+3=4,
∴BG=DT=4.
当点 F在点 D 的左侧时,如下图,同法可得 MD = BG = 3 - 1 =2(同学们自行写出过程).
巩固练习
【巩固练习1】
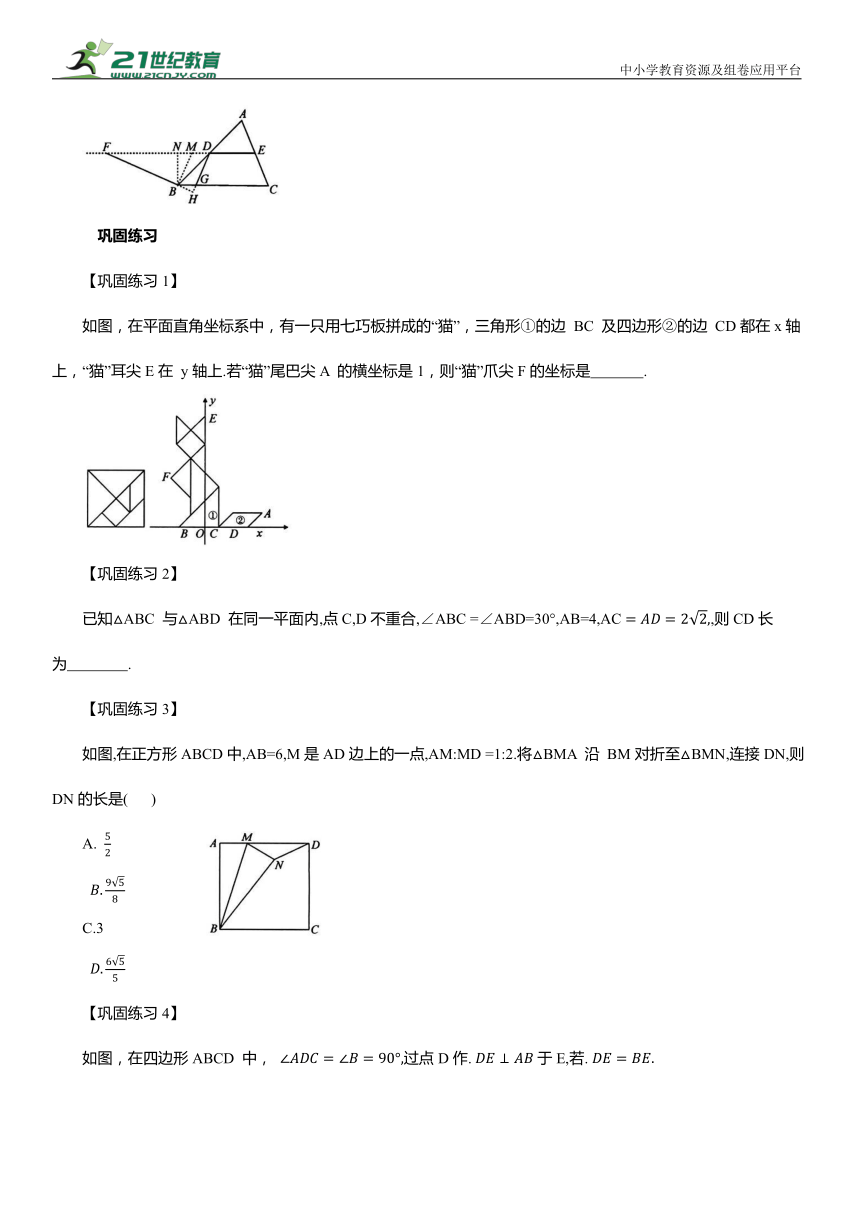
如图,在平面直角坐标系中,有一只用七巧板拼成的“猫”,三角形①的边 BC 及四边形②的边 CD都在x轴上,“猫”耳尖E在 y轴上.若“猫”尾巴尖A 的横坐标是1,则“猫”爪尖F的坐标是 .
【巩固练习2】
已知△ABC 与△ABD 在同一平面内,点C,D不重合,∠ABC =∠ABD=30°,AB=4,AC ,则CD长为 .
【巩固练习3】
如图,在正方形ABCD中,AB=6,M是AD边上的一点,AM:MD =1:2.将△BMA 沿 BM对折至△BMN,连接DN,则DN的长是( )
A.
C.3
【巩固练习4】
如图,在四边形ABCD 中, 过点D作. 于E,若.
(1)求证:
(2)连接AC 交 DE 于点 F,若∠ADE =30°,AD =6,求 DF 的长.
【巩固练习5】
在△ABC 中,∠ACB =90°,分别过点 B,C作∠BAC平分线的垂线,垂足分别为点D,E,BC的中点是M,连接CD,MD,ME.则下列结论错误的是 ( )
A. CD=2ME B. ME//AB
C. BD=CD D. ME=MD
【巩固练习6】
如图,在等腰直角三角形ABC 中,∠ACB=90°,AC = BC =2 边长为2 的正方形DEFG 的对角线交点与点 C 重合,连接AD,BE.
(1)求证:
(2)当点 D 在. 内部,且 时,设AC 与DG 相交于点 M,求AM 的长;
(3)将正方形 DEFG绕点 C 旋转一周,当点A、D、E三点在同一直线上时,请直接写出AD 的长.
【巩固练习7】
[问题提出]如图(1),在△ABC 和△DEC中,∠ACB =∠DCE =90°,BC =AC,EC =DC,点 E 在△ABC 内部,直线AD 与BE 交于点 F,线段AF,BF,CF 之间存在怎样的数量关系
[问题探究](1)先将问题特殊化.如图(2),当点D,F重合时,直接写出一个等式,表示AF,BF,CF 之间的数量关系;
(2)再探究一般情形.如图①,当点 D,F不重合时,证明(1)中的结论仍然成立.
[问题拓展]如图③,在△ABC 和△DEC中,∠ACB=∠DCE =90°,BC =kAC,EC =kDC(k是常数),点 E 在△ABC 内部,直线AD 与BE 交于点 F,直接写出一个等式,表示线段AF,BF,CF 之间的数量关系.
1.思路分析:设大正方形的边长为2a,则大等腰直角三角形的腰长为 中等腰直角三角形的腰长为a,小等腰直角三角形的腰长为 小正方形的边长为 平行四边形的长边为a,短边为 用含有a的代数式表示点A的横坐标,表示点F的坐标,确定a值即可.故答案为
2.如图, 当C, D同侧时, 过点A作AE⊥CD于E.
在Rt△AEB中, ∠AEB=90°, AB=4, ∠ABE=30°,
∴DE=EC = AE,
∴△ADC是等腰直角三角形,
∴CD=4,
当C, D异侧时, 过C'作( 于H,
∵△BCC'是等边三角形, BC =BE﹣EC=2 ﹣2,
在Rt△DC'H中,
∵△DBD'是等边三角形,
∴CD的长为 或4或
3.连接AN交BM于点O, 作 于点H.如图:
∵四边形ABCD是正方形.
根据折叠性质, AO⊥BM, AO=ON. AM=MN=2.
故选: D.
4.(1)证明: 作DG⊥BC, 交BC的延长线于点G,如图所示,∵DE⊥AB, ∠B=90°,DG⊥BC,
∴∠DEB=∠B=∠BGD =90°,
∴四边形DEBG是矩形,又∵DE=BE,
∴四边形DEBG是正方形,
∴DG =BE, ∠EDG=90°,
∴DG =DE, ∠EDC+∠CDG=90°,
∵∠ADC=90°,
∴∠EDC+∠ADE=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,
∴△ADE≌△CDG(ASA),
∴DA=DC;
)由 (1) 知, ,四边形DEBG是正方形,
即
解得
即DF的长是( )
5.根据题意可作出图形,如图所示,并延长EM交BD于点F,延长DM交AB于点N,
在△ABC中, ∠ACB=90°, 分别过点B, C作∠BAC平分线的垂线,垂足分别为点D,E,
∵∠ADB=90°=∠ACB,
∴D点在△ABC的外接圆上, 即点A, C, D, B四点在同一圆上,
∵AD平分∠CAB,
∴∠CAD=∠BAD,
∴CD = DB, 故选项A正确;
∵点M是BC的中点,
∴DM⊥BC, 又∵∠ACB = 90°,
∴AC∥DN,
∴点N是线段AB的中点, ∴AN = DN,
∴∠DAB=∠ADN,
∵CE⊥AD, BD⊥AD,
∴CE∥BD,
∴∠ECM =∠FBM, ∠CEM =∠BFM,
∵点M是BC的中点,∴CM = BM,
在△CEM和△BFM中,
∴△CEM≌△BFM(AAS),
∴EM =FM,∴EM =FM = DM, 故选项D正确;
∴∠FED =∠MDE =∠DAB,
∴EM∥AB, 故选项B正确,
综上,可知选项C的结论不一定正确.
故选: C.
6.(1) 如图1, ∵四边形
DEFG是正方形,
∴∠DCE=90°,
CD=CE;
∵∠ACB=90°,
∴∠ACD=∠BCE=90°-∠BCD,在△ACD和△BCE中,
∴△ACD≌△BCE(SAS).
(2)如图2, 过点M作MH⊥AD于点H, 则∠AHM = ∠DHM = 90°.
∵∠DCG=90°, CD=CG,
∴∠CDG=∠CGD=45°,
∵∠ADC=90°,
(3)如图3,A、D、E三点在同一直线上,且点D在点A和点E之间.
由 得
由△ACD≌△BCE,得∠BEC =∠ADC =135°,
∴∠BEC+∠CEF=180°,
∴点B、E、F在同一条直线上,
∴∠AEB=90°,
且DE=2, AD=BE,
解得 或 (不符合题意,舍去);
如图4, A、D、E三点在同一直线上,且点D在AE的延长线上.
∵∠BCF =∠ACE=90°--∠ACF, BC=AC, CF =CE
∴△BCF≌△ACE(SAS),
∴∠BFC =∠AEC,
∵∠CFE=∠CED=45°,
∴∠BFC+∠CFE=∠AEC+∠CED=180°,
∴点B、F、E在同一条直线上;
∵AC=BC, ∠ACD=∠BCE=90°+∠ACE,CD=CE,
∴△ACD≌△BCE(SAS),
解得 或 (不符合题意,舍去)。
综上所述,AD的长为 或
7.(1)结论:
理由: 如图(2), ∵∠ACD+∠ACE=90°,
∠ACE+∠BCE=90°,
∴∠BCE=∠ACD,
∵BC =AC, EC=DC,
∴△ACD≌△BCE(SAS),
∴BE = AD, ∠EBC =∠CAD,
而点D、F重合, 故BE= AD = AF,
而△CDE为等腰直角三角形,
故
则.BF=BD =BE+ED=AF+ CF,
即
(2)证明: 如图(1), 由 (1) 知,△ACD≌△BCE(SAS),
∴∠CAF =∠CBE, BE= AD,
过点C作 交BF于点G,
∵∠ACF+∠ACG=90°,∠ACG+∠GCB=90°,
∴∠ACF=∠BCG,
∵∠CAF =∠CBE, BC = AC,
∴△BCG≌△ACF(ASA),
∴GC=FC, BG=AF,
故△GCF为等腰直角三角形,则
即
(3)结论:
理由: 由 (2) 知, 而 即
过点C作 交BF于点G,
由 (2) 知,
则
在 中,
则. ,即
垂线相关的辅助线
典例精析
【典型题1】★· 如图所示,△ABC 中,AB=AC,∠BAC =120°,AC 的垂直平分线 EF 交AC 于点E,交 BC 于点 F.求证:BF=2CF.
【思路分析】思路一(正向推导法):从题目条件分析,EF 是AC 的垂直平分线,因此连接AF,可得AF=FC,即将要证明BF=2CF转化为证明BF =2AF,再由已知角度容易得出∠B=30°,∠BAF=90°,可得BF=2AF.
思路二(逆向分析法):从结论出发分析,要证明BF=2CF,自然想到应用“直角三角形30°角所对的直角边等于斜边的一半”这条性质,再从题目条件“AB=AC,∠BAC=120°”求出∠B = ∠C = 30°,从而连接 AF 构造Rt△BAF,又根据中垂线定理可得AF =CF,问题得证.
【答案解析】解:连接AF,
∵AB=AC ,∴∠B=∠C;
又∵∠BAC=120°,∴∠B+∠C=60°
∴∠B=∠C=30°,
∵ EF 垂直平分AC∴ FA =FC,
∴∠FAC=∠C=30°,
又∵∠BAC=120°,
∵∠B=30°∴BF=2AF,
∵FA=FC ∴BF=2CF.
【规律总结】辅助线作法:方法①:垂直平分连两端.方法②:构造特殊三角形.
【典型题2】★★★如图,在△ABC中,∠B=45°,AB=6 ,D、E分别是AB、AC的中点,连接DE,在直线DE 和直线BC 上分别取点F、G,连接BF、DG.若BF=3DG,且直线BF与直线DG互相垂直,则BG的长为 .
【思路分析】本题比较难,需从题目条件入手分析,正向推导,作垂线构造直角三角形.注意需分点 F 在点 D 的两侧分类讨论.
注:本题同学们也可尝试其他方法,比如过点 F 作BF的垂线(或者DG的平行线,道理相同,目的是构造直角三角形).
【答案解析】解:如图,当点 F 在点 D 的右侧时,过点 B 作 BT⊥BF 交 ED的延长线于T,过点 B 作 BH⊥DT于 H.
∵DG⊥BF,BT⊥BF,∴DG//BT,
∵AD=DB,AE=EC,∴DE//BC,
∴四边形DGBT是平行四边形,
∴BG=DT,DG=BT,
∠BDH=∠ABC=45°,
∵∠TBF=∠BHF=90°,
∴∠TBH+∠FBH=90°,
∵∠FBH+∠F=90°,
∴∠TBH=∠F,
∴TH=1,∴DT=TH+DH=1+3=4,
∴BG=DT=4.
当点 F在点 D 的左侧时,如下图,同法可得 MD = BG = 3 - 1 =2(同学们自行写出过程).
巩固练习
【巩固练习1】
如图,在平面直角坐标系中,有一只用七巧板拼成的“猫”,三角形①的边 BC 及四边形②的边 CD都在x轴上,“猫”耳尖E在 y轴上.若“猫”尾巴尖A 的横坐标是1,则“猫”爪尖F的坐标是 .
【巩固练习2】
已知△ABC 与△ABD 在同一平面内,点C,D不重合,∠ABC =∠ABD=30°,AB=4,AC ,则CD长为 .
【巩固练习3】
如图,在正方形ABCD中,AB=6,M是AD边上的一点,AM:MD =1:2.将△BMA 沿 BM对折至△BMN,连接DN,则DN的长是( )
A.
C.3
【巩固练习4】
如图,在四边形ABCD 中, 过点D作. 于E,若.
(1)求证:
(2)连接AC 交 DE 于点 F,若∠ADE =30°,AD =6,求 DF 的长.
【巩固练习5】
在△ABC 中,∠ACB =90°,分别过点 B,C作∠BAC平分线的垂线,垂足分别为点D,E,BC的中点是M,连接CD,MD,ME.则下列结论错误的是 ( )
A. CD=2ME B. ME//AB
C. BD=CD D. ME=MD
【巩固练习6】
如图,在等腰直角三角形ABC 中,∠ACB=90°,AC = BC =2 边长为2 的正方形DEFG 的对角线交点与点 C 重合,连接AD,BE.
(1)求证:
(2)当点 D 在. 内部,且 时,设AC 与DG 相交于点 M,求AM 的长;
(3)将正方形 DEFG绕点 C 旋转一周,当点A、D、E三点在同一直线上时,请直接写出AD 的长.
【巩固练习7】
[问题提出]如图(1),在△ABC 和△DEC中,∠ACB =∠DCE =90°,BC =AC,EC =DC,点 E 在△ABC 内部,直线AD 与BE 交于点 F,线段AF,BF,CF 之间存在怎样的数量关系
[问题探究](1)先将问题特殊化.如图(2),当点D,F重合时,直接写出一个等式,表示AF,BF,CF 之间的数量关系;
(2)再探究一般情形.如图①,当点 D,F不重合时,证明(1)中的结论仍然成立.
[问题拓展]如图③,在△ABC 和△DEC中,∠ACB=∠DCE =90°,BC =kAC,EC =kDC(k是常数),点 E 在△ABC 内部,直线AD 与BE 交于点 F,直接写出一个等式,表示线段AF,BF,CF 之间的数量关系.
1.思路分析:设大正方形的边长为2a,则大等腰直角三角形的腰长为 中等腰直角三角形的腰长为a,小等腰直角三角形的腰长为 小正方形的边长为 平行四边形的长边为a,短边为 用含有a的代数式表示点A的横坐标,表示点F的坐标,确定a值即可.故答案为
2.如图, 当C, D同侧时, 过点A作AE⊥CD于E.
在Rt△AEB中, ∠AEB=90°, AB=4, ∠ABE=30°,
∴DE=EC = AE,
∴△ADC是等腰直角三角形,
∴CD=4,
当C, D异侧时, 过C'作( 于H,
∵△BCC'是等边三角形, BC =BE﹣EC=2 ﹣2,
在Rt△DC'H中,
∵△DBD'是等边三角形,
∴CD的长为 或4或
3.连接AN交BM于点O, 作 于点H.如图:
∵四边形ABCD是正方形.
根据折叠性质, AO⊥BM, AO=ON. AM=MN=2.
故选: D.
4.(1)证明: 作DG⊥BC, 交BC的延长线于点G,如图所示,∵DE⊥AB, ∠B=90°,DG⊥BC,
∴∠DEB=∠B=∠BGD =90°,
∴四边形DEBG是矩形,又∵DE=BE,
∴四边形DEBG是正方形,
∴DG =BE, ∠EDG=90°,
∴DG =DE, ∠EDC+∠CDG=90°,
∵∠ADC=90°,
∴∠EDC+∠ADE=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,
∴△ADE≌△CDG(ASA),
∴DA=DC;
)由 (1) 知, ,四边形DEBG是正方形,
即
解得
即DF的长是( )
5.根据题意可作出图形,如图所示,并延长EM交BD于点F,延长DM交AB于点N,
在△ABC中, ∠ACB=90°, 分别过点B, C作∠BAC平分线的垂线,垂足分别为点D,E,
∵∠ADB=90°=∠ACB,
∴D点在△ABC的外接圆上, 即点A, C, D, B四点在同一圆上,
∵AD平分∠CAB,
∴∠CAD=∠BAD,
∴CD = DB, 故选项A正确;
∵点M是BC的中点,
∴DM⊥BC, 又∵∠ACB = 90°,
∴AC∥DN,
∴点N是线段AB的中点, ∴AN = DN,
∴∠DAB=∠ADN,
∵CE⊥AD, BD⊥AD,
∴CE∥BD,
∴∠ECM =∠FBM, ∠CEM =∠BFM,
∵点M是BC的中点,∴CM = BM,
在△CEM和△BFM中,
∴△CEM≌△BFM(AAS),
∴EM =FM,∴EM =FM = DM, 故选项D正确;
∴∠FED =∠MDE =∠DAB,
∴EM∥AB, 故选项B正确,
综上,可知选项C的结论不一定正确.
故选: C.
6.(1) 如图1, ∵四边形
DEFG是正方形,
∴∠DCE=90°,
CD=CE;
∵∠ACB=90°,
∴∠ACD=∠BCE=90°-∠BCD,在△ACD和△BCE中,
∴△ACD≌△BCE(SAS).
(2)如图2, 过点M作MH⊥AD于点H, 则∠AHM = ∠DHM = 90°.
∵∠DCG=90°, CD=CG,
∴∠CDG=∠CGD=45°,
∵∠ADC=90°,
(3)如图3,A、D、E三点在同一直线上,且点D在点A和点E之间.
由 得
由△ACD≌△BCE,得∠BEC =∠ADC =135°,
∴∠BEC+∠CEF=180°,
∴点B、E、F在同一条直线上,
∴∠AEB=90°,
且DE=2, AD=BE,
解得 或 (不符合题意,舍去);
如图4, A、D、E三点在同一直线上,且点D在AE的延长线上.
∵∠BCF =∠ACE=90°--∠ACF, BC=AC, CF =CE
∴△BCF≌△ACE(SAS),
∴∠BFC =∠AEC,
∵∠CFE=∠CED=45°,
∴∠BFC+∠CFE=∠AEC+∠CED=180°,
∴点B、F、E在同一条直线上;
∵AC=BC, ∠ACD=∠BCE=90°+∠ACE,CD=CE,
∴△ACD≌△BCE(SAS),
解得 或 (不符合题意,舍去)。
综上所述,AD的长为 或
7.(1)结论:
理由: 如图(2), ∵∠ACD+∠ACE=90°,
∠ACE+∠BCE=90°,
∴∠BCE=∠ACD,
∵BC =AC, EC=DC,
∴△ACD≌△BCE(SAS),
∴BE = AD, ∠EBC =∠CAD,
而点D、F重合, 故BE= AD = AF,
而△CDE为等腰直角三角形,
故
则.BF=BD =BE+ED=AF+ CF,
即
(2)证明: 如图(1), 由 (1) 知,△ACD≌△BCE(SAS),
∴∠CAF =∠CBE, BE= AD,
过点C作 交BF于点G,
∵∠ACF+∠ACG=90°,∠ACG+∠GCB=90°,
∴∠ACF=∠BCG,
∵∠CAF =∠CBE, BC = AC,
∴△BCG≌△ACF(ASA),
∴GC=FC, BG=AF,
故△GCF为等腰直角三角形,则
即
(3)结论:
理由: 由 (2) 知, 而 即
过点C作 交BF于点G,
由 (2) 知,
则
在 中,
则. ,即
同课章节目录
