2025中考数学复习--动点在二次函数图象中的分类讨论(基础训练) (含解析)
文档属性
| 名称 | 2025中考数学复习--动点在二次函数图象中的分类讨论(基础训练) (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 364.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 06:36:52 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
动点在二次函数图象中的分类讨论
【专题说明】
关于二次函数动点问题的解答方法
⑴ 求二次函数的图象与x轴的交点坐标,需转化为一元二次方程;
⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;
⑶ 根据图象的位置判断二次函数ax +bx+c=0中a,b,c的符号,或由二次函数中a,b,c的符号判断图象的位置,要数形结合;
⑷ 二次函数的图象关于
对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x轴的一个交点坐标,可由对称性求出另一个交点坐标.
⑸ 与二次函数有关的还有二次三项式,二次三项式ax +bx+c﹙a≠0﹚本身就是所含字母x的二次函数;
【精典例题】
1、如图1,已知抛物线y=x2-x-n(n>0)与x轴交于A,B两点(A点在B点的左边),与y轴交于点C.
(1)若△ABC为直角三角形,求n的值;
(2)在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,若以BC为边,以点B,C,P,Q为顶点的四边形是平行四边形,求P点的坐标;
(3)如图2,过点A作直线BC的平行线交抛物线于另一点D,交y轴于点E,若AE∶ED=1∶4.求n的值.
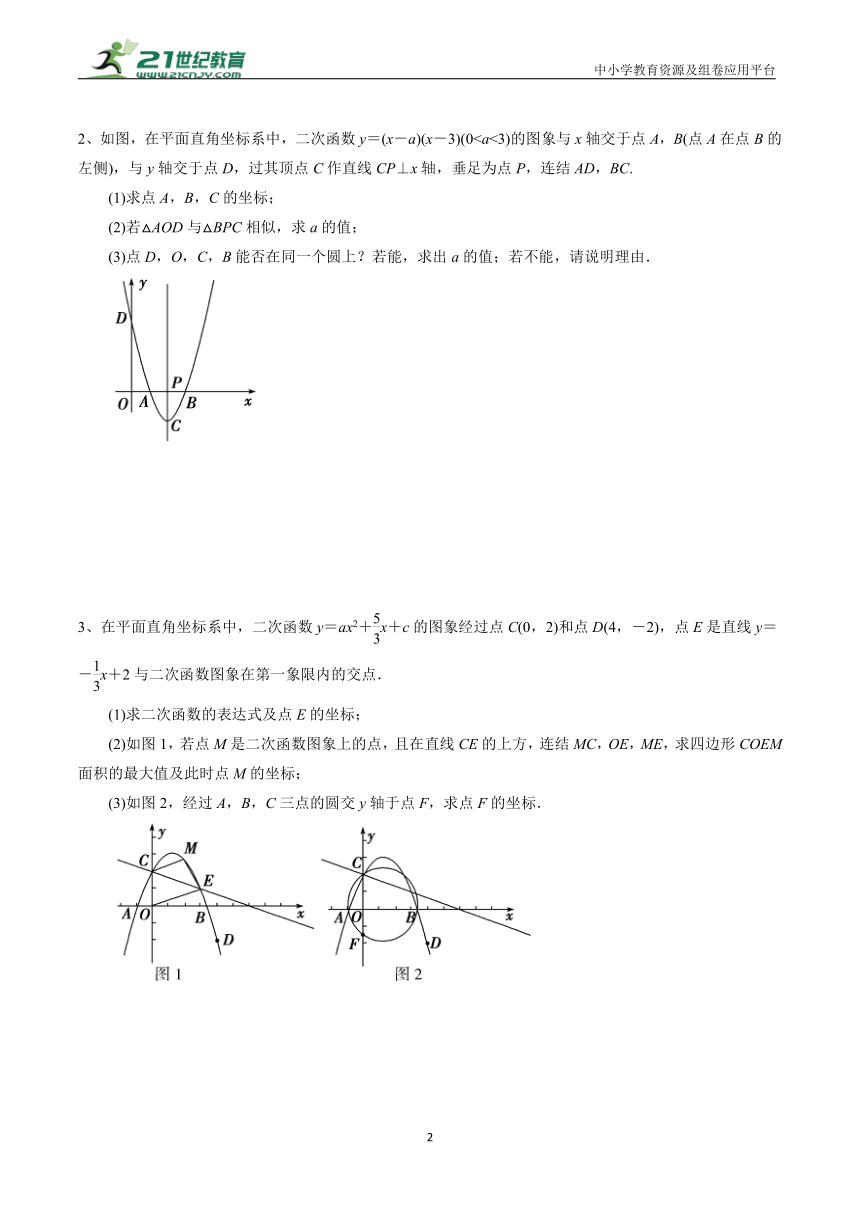
2、如图,在平面直角坐标系中,二次函数y=(x-a)(x-3)(0(1)求点A,B,C的坐标;
(2)若△AOD与△BPC相似,求a的值;
(3)点D,O,C,B能否在同一个圆上?若能,求出a的值;若不能,请说明理由.
3、在平面直角坐标系中,二次函数y=ax2+x+c的图象经过点C(0,2)和点D(4,-2),点E是直线y=-x+2与二次函数图象在第一象限内的交点.
(1)求二次函数的表达式及点E的坐标;
(2)如图1,若点M是二次函数图象上的点,且在直线CE的上方,连结MC,OE,ME,求四边形COEM面积的最大值及此时点M的坐标;
(3)如图2,经过A,B,C三点的圆交y轴于点F,求点F的坐标.
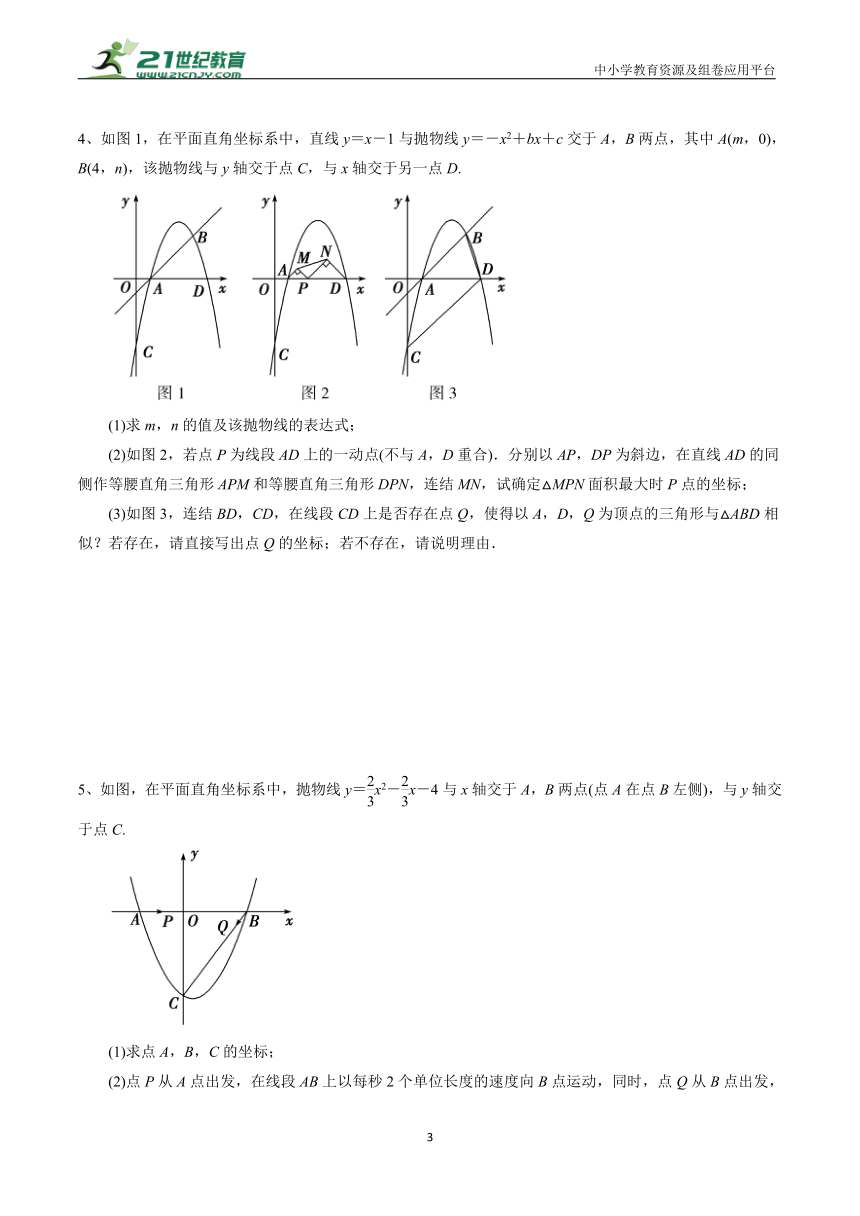
4、如图1,在平面直角坐标系中,直线y=x-1与抛物线y=-x2+bx+c交于A,B两点,其中A(m,0),B(4,n),该抛物线与y轴交于点C,与x轴交于另一点D.
(1)求m,n的值及该抛物线的表达式;
(2)如图2,若点P为线段AD上的一动点(不与A,D重合).分别以AP,DP为斜边,在直线AD的同侧作等腰直角三角形APM和等腰直角三角形DPN,连结MN,试确定△MPN面积最大时P点的坐标;
(3)如图3,连结BD,CD,在线段CD上是否存在点Q,使得以A,D,Q为顶点的三角形与△ABD相似?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
5、如图,在平面直角坐标系中,抛物线y=x2-x-4与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)点P从A点出发,在线段AB上以每秒2个单位长度的速度向B点运动,同时,点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,当其中一个点达到终点时,另一个点也停止运动.设运动时间为t s,求运动时间t为多少秒时,△PBQ的面积S最大,并求出其最大面积;
(3)在(2)的条件下,当△PBQ的面积最大时,在BC下方的抛物线上是否存在点M,使△BMC的面积是△PBQ的面积的1.6倍?若存在,求点M的坐标;若不存在,请说明理由.
6、抛物线L:y=-x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.
(1)直接写出抛物线L的表达式;
(2)如图1,过定点的直线y=kx-k+4(k<0)与抛物线L交于点M,N.若△BMN的面积等于1,求k的值;
(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D,F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点.若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.
1.解:(1)若△ABC为直角三角形,则由Rt△AOC∽Rt△COB可得OC2=OA·OB,
由抛物线y=x2-x-n(n>0),可得OC=n,OA·OB=2n,
∴n2=2n,解得n1=2,n2=0(舍去).∴n=2;
(2)由(1)可知抛物线的对称轴为x=,抛物线表达式为y=x2-x-2,
令y=0,得x1=-1,x2=4,∴A(-1,0),B(4,0),
设点P.
①如答图①,当直线PQ∥BC时,
当点P在点Q的左侧,
答图①
△BOC平移到△QNP的位置时,四边形PQBC为平行四边形,
此时NQ=OB,即-m=4,m=-.
m2-m-2=,此时点P坐标为;
当点P在点Q的右侧时,
同理可得m-=4,解得m=.
m2-m-2=,
此时点P的坐标为.
答图②
②当直线PQ与直线BC相交时,如答图②,
此时点P到y轴的距离等于点B到对称轴的距离,
即m=4-=,m2-m-2=-,此时点P的坐标为.
综上所述,满足条件的点P的坐标为,,;
答图③
(3)如答图③,过点D作DF⊥x轴,垂足为F.
则AO∶OF=AE∶ED=1∶4,
设A(a,0),B(b,0),则AO=-a,OF=-4a,
∵AD∥BC,
∴∠DAO=∠OBC,
∵∠AFD=∠BOC=90°,∴△BOC∽△AFD,
∴=,即=,
由题意得ab=-2n,∴=-,
∴DF=-5a·=-5a·(-)=a2,
∵点A,D在抛物线上,
∴
解得∴n的值为.
2.解:(1)y=(x-a)(x-3),当y=0时,x1=a,x2=3,
∴A(a,0),B(3,0).
当x=0时,y=3a,∴D(0,3a);
(2)如答图①,连结AD,BC,
由(1)可得OA=a,OD=3a,BP=,OP=+a=,
答图①
将x=代入二次函数,得y=-,
∴PC=.
①当△DOA∽△CPB时,
有=,即=,
解得a=0(舍去)或-3(舍去).
②当△DOA∽△BPC时,
有=,即=,解得a=.
综上,当△AOD与△BPC相似时,a=;
答图②
(3)能.如答图②,连结BD,设BD的中点为M.
∵D,O,B三点共圆,且圆心为M,
假设点C也在此圆上,则应有MC=MB,
∴+=+,
解得a1=,a2=-(舍去),a3=-3(舍去),a4=3(舍去),
∴当a的值为时,D,O,C,B四点共圆.
3.解:(1)∵二次函数y=ax2+x+c的图象经过点C(0,2)和点D(4,-2),
∴解得
∴二次函数表达式为y=-x2+x+2,
与y=-x+2联立,解得x1=0(舍去),x2=3,此时y=1,故E(3,1);
(2)S四边形COEM=S△COE+S△CME,S△COE=·CO·,∵C(0,2),E(3,1),∴S△COE=3,S△CME=·CE·h(h为点M到CE的距离),
∵M在抛物线上运动,∴当平行于CE的直线与抛物线相切于点M时,h最大,从而面积最大,
设l′的表达式为y=-x+b,
与y=-x2+x+2联立,
得-x+b=-x2+x+2,
Δ=36+8(6-3b)=0,解得b=,
此时点M坐标为,
如答图①,过M作MN∥y轴,交CE于点N,
在y=-x+2中,令x=,得y=,
∴N,
∴S△CME=·MN·=,
∴S四边形COEM=S△COE+S△CME=;
答图①
(3)在y=-x2+x+2中,令y=0,得x1=,x2=,
∴OA=,OB=,
答图②
如答图②,连结BF,AC,
∵∠ACO=∠ABF,∠AOC=∠FOB,
∴△AOC∽△FOB,
∴=,即=,解得OF=,
∴F.
4.解:(1)把点A(m,0),点B(4,n)代入x-y=1,得m=1,n=3,
∴A(1,0),B(4,3),
代入y=-x2+bx+c,得
解得
∴y=-x2+6x-5;
(2)∵△APM和△DPN为等腰直角三角形,
∴∠APM=∠DPN=45°,
∴∠MPN=90°,
∴△MPN为直角三角形.
令-x2+6x-5=0,解得x1=1,x2=5,
∴D(5,0),AD=4.
设AP=m,则DP=4-m,PM=m,PN=(4-m),
∴S△MPN=PM·PN=×m·(4-m)
=-m2+m=-(m-2)2+1,
∴当m=2,即AP=2时,S△MPN最大,此时OP=3,∴P(3,0);
(3)存在,点Q坐标为(2,-3)或.
由A(1,0),B(4,3),C(0,-5),D(5,0),得AB=3,AD=4,直线CD的函数表达式为y=x-5,∴∠BAD=∠CDO=45°,分两种情况讨论:
①当△ADQ∽△DAB时,=,
∴DQ=AB=3,
答图
如答图,过Q点作x轴的垂线,垂足为E,则DE=EQ=DQ=3,
∵D(5,0),∴Q(2,-3);
②当△QDA∽△DAB时,=,
∴=,解得DQ=,
同上得Q坐标为.
综上,存在点Q坐标为(2,-3)或.
5.解:(1)令y=0,得x2-x-4=0,解得x1=-2,x2=3;
令x=0,得y=-4,
故A(-2,0),B(3,0),C(0,-4);
答图①
(2)如答图①,过点Q作QD⊥AB于点D,则AP=2t,BQ=t,BO=3,AB=5,OC=4,BC==5,PB=5-2t.
∵DQ∥OC,
∴△BDQ∽△BOC,
∴=,即=,
解得DQ=t.
∴S△PBQ=PB·DQ=×t×(5-2t)=-t2+2t=-+,
∴当t=时,S△PBQ取最大值为;
答图②
(3)存在,M的坐标为(1,-4)或.
设M,直线BC的表达式为y=kx-4,
则3k-4=0,解得k=,
∴直线BC的表达式为y=x-4,
如答图②,过M作ME⊥AB交BC于点N,则N,
∴MN=m-4-=-m2+2m,
∴S△MBC=S△CMN+S△BMN=MN·OB=-m2+3m,
∵△BMC的面积是△PBQ的面积的1.6倍,
∴-m2+3m=1.6×,整理得m2-3m+2=0,解得m1=1,m2=2.
∴M(1,-4)或.
6.解:(1)由题意知解得
∴抛物线L的表达式为y=-x2+2x+1;
(2)∵y=kx-k+4=k(x-1)+4,
当x=1时,y=4,
∴该直线过定点G(1,4),如答图,
答图
∵y=-x2+2x+1=-(x-1)2+2,
∴点B(1,2),∴BG=2,
∵S△BMN=1,即S△BNG-S△BMG=BG·(xN-1)-BG·(xM-1)=1,
∴xN-xM=1,
由得x2+(k-2)x-k+3=0,
于是xM+xN=2-k,xM·xN=3-k,
故xN-xM==.
由xN-xM=1得=1,
∵k<0,∴k=-3;
(3)设抛物线L1的表达式为y=-x2+2x+1+m,P(0,t),
∴C(0,1+m),D(2,1+m),F(1,0),
当△PCD∽△FOP时,=,
∴=,整理得t2-(1+m)t+2=0;①
当△PCD∽△POF时,=,
∴=,整理得t=(m+1).②
Ⅰ.当方程①有两个相等实数根时,
Δ=(1+m)2-8=0,解得m=2-1(负值舍去),
此时方程①有两个相等实数根t1=t2=,方程②有一个实数根t=,
∴m=2-1,
∴点P的坐标为(0,)或;
Ⅱ.当方程①有两个不相等的实数根时,
把②代入①,得(m+1)2-(m+1)2+2=0,
解得m=2(负值舍去),
此时方程①有两个不相等的实数根t1=1,t2=2,方程②有一个实数根t=1,
∴m=2,
∴点P的坐标为(0,1)或(0,2).
综上,当m=2-1时,点P的坐标为(0,)或;当m=2时,点P的坐标为(0,1)或(0,2).
动点在二次函数图象中的分类讨论
【专题说明】
关于二次函数动点问题的解答方法
⑴ 求二次函数的图象与x轴的交点坐标,需转化为一元二次方程;
⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;
⑶ 根据图象的位置判断二次函数ax +bx+c=0中a,b,c的符号,或由二次函数中a,b,c的符号判断图象的位置,要数形结合;
⑷ 二次函数的图象关于
对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x轴的一个交点坐标,可由对称性求出另一个交点坐标.
⑸ 与二次函数有关的还有二次三项式,二次三项式ax +bx+c﹙a≠0﹚本身就是所含字母x的二次函数;
【精典例题】
1、如图1,已知抛物线y=x2-x-n(n>0)与x轴交于A,B两点(A点在B点的左边),与y轴交于点C.
(1)若△ABC为直角三角形,求n的值;
(2)在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,若以BC为边,以点B,C,P,Q为顶点的四边形是平行四边形,求P点的坐标;
(3)如图2,过点A作直线BC的平行线交抛物线于另一点D,交y轴于点E,若AE∶ED=1∶4.求n的值.
2、如图,在平面直角坐标系中,二次函数y=(x-a)(x-3)(0
(2)若△AOD与△BPC相似,求a的值;
(3)点D,O,C,B能否在同一个圆上?若能,求出a的值;若不能,请说明理由.
3、在平面直角坐标系中,二次函数y=ax2+x+c的图象经过点C(0,2)和点D(4,-2),点E是直线y=-x+2与二次函数图象在第一象限内的交点.
(1)求二次函数的表达式及点E的坐标;
(2)如图1,若点M是二次函数图象上的点,且在直线CE的上方,连结MC,OE,ME,求四边形COEM面积的最大值及此时点M的坐标;
(3)如图2,经过A,B,C三点的圆交y轴于点F,求点F的坐标.
4、如图1,在平面直角坐标系中,直线y=x-1与抛物线y=-x2+bx+c交于A,B两点,其中A(m,0),B(4,n),该抛物线与y轴交于点C,与x轴交于另一点D.
(1)求m,n的值及该抛物线的表达式;
(2)如图2,若点P为线段AD上的一动点(不与A,D重合).分别以AP,DP为斜边,在直线AD的同侧作等腰直角三角形APM和等腰直角三角形DPN,连结MN,试确定△MPN面积最大时P点的坐标;
(3)如图3,连结BD,CD,在线段CD上是否存在点Q,使得以A,D,Q为顶点的三角形与△ABD相似?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
5、如图,在平面直角坐标系中,抛物线y=x2-x-4与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)求点A,B,C的坐标;
(2)点P从A点出发,在线段AB上以每秒2个单位长度的速度向B点运动,同时,点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,当其中一个点达到终点时,另一个点也停止运动.设运动时间为t s,求运动时间t为多少秒时,△PBQ的面积S最大,并求出其最大面积;
(3)在(2)的条件下,当△PBQ的面积最大时,在BC下方的抛物线上是否存在点M,使△BMC的面积是△PBQ的面积的1.6倍?若存在,求点M的坐标;若不存在,请说明理由.
6、抛物线L:y=-x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.
(1)直接写出抛物线L的表达式;
(2)如图1,过定点的直线y=kx-k+4(k<0)与抛物线L交于点M,N.若△BMN的面积等于1,求k的值;
(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D,F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点.若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.
1.解:(1)若△ABC为直角三角形,则由Rt△AOC∽Rt△COB可得OC2=OA·OB,
由抛物线y=x2-x-n(n>0),可得OC=n,OA·OB=2n,
∴n2=2n,解得n1=2,n2=0(舍去).∴n=2;
(2)由(1)可知抛物线的对称轴为x=,抛物线表达式为y=x2-x-2,
令y=0,得x1=-1,x2=4,∴A(-1,0),B(4,0),
设点P.
①如答图①,当直线PQ∥BC时,
当点P在点Q的左侧,
答图①
△BOC平移到△QNP的位置时,四边形PQBC为平行四边形,
此时NQ=OB,即-m=4,m=-.
m2-m-2=,此时点P坐标为;
当点P在点Q的右侧时,
同理可得m-=4,解得m=.
m2-m-2=,
此时点P的坐标为.
答图②
②当直线PQ与直线BC相交时,如答图②,
此时点P到y轴的距离等于点B到对称轴的距离,
即m=4-=,m2-m-2=-,此时点P的坐标为.
综上所述,满足条件的点P的坐标为,,;
答图③
(3)如答图③,过点D作DF⊥x轴,垂足为F.
则AO∶OF=AE∶ED=1∶4,
设A(a,0),B(b,0),则AO=-a,OF=-4a,
∵AD∥BC,
∴∠DAO=∠OBC,
∵∠AFD=∠BOC=90°,∴△BOC∽△AFD,
∴=,即=,
由题意得ab=-2n,∴=-,
∴DF=-5a·=-5a·(-)=a2,
∵点A,D在抛物线上,
∴
解得∴n的值为.
2.解:(1)y=(x-a)(x-3),当y=0时,x1=a,x2=3,
∴A(a,0),B(3,0).
当x=0时,y=3a,∴D(0,3a);
(2)如答图①,连结AD,BC,
由(1)可得OA=a,OD=3a,BP=,OP=+a=,
答图①
将x=代入二次函数,得y=-,
∴PC=.
①当△DOA∽△CPB时,
有=,即=,
解得a=0(舍去)或-3(舍去).
②当△DOA∽△BPC时,
有=,即=,解得a=.
综上,当△AOD与△BPC相似时,a=;
答图②
(3)能.如答图②,连结BD,设BD的中点为M.
∵D,O,B三点共圆,且圆心为M,
假设点C也在此圆上,则应有MC=MB,
∴+=+,
解得a1=,a2=-(舍去),a3=-3(舍去),a4=3(舍去),
∴当a的值为时,D,O,C,B四点共圆.
3.解:(1)∵二次函数y=ax2+x+c的图象经过点C(0,2)和点D(4,-2),
∴解得
∴二次函数表达式为y=-x2+x+2,
与y=-x+2联立,解得x1=0(舍去),x2=3,此时y=1,故E(3,1);
(2)S四边形COEM=S△COE+S△CME,S△COE=·CO·,∵C(0,2),E(3,1),∴S△COE=3,S△CME=·CE·h(h为点M到CE的距离),
∵M在抛物线上运动,∴当平行于CE的直线与抛物线相切于点M时,h最大,从而面积最大,
设l′的表达式为y=-x+b,
与y=-x2+x+2联立,
得-x+b=-x2+x+2,
Δ=36+8(6-3b)=0,解得b=,
此时点M坐标为,
如答图①,过M作MN∥y轴,交CE于点N,
在y=-x+2中,令x=,得y=,
∴N,
∴S△CME=·MN·=,
∴S四边形COEM=S△COE+S△CME=;
答图①
(3)在y=-x2+x+2中,令y=0,得x1=,x2=,
∴OA=,OB=,
答图②
如答图②,连结BF,AC,
∵∠ACO=∠ABF,∠AOC=∠FOB,
∴△AOC∽△FOB,
∴=,即=,解得OF=,
∴F.
4.解:(1)把点A(m,0),点B(4,n)代入x-y=1,得m=1,n=3,
∴A(1,0),B(4,3),
代入y=-x2+bx+c,得
解得
∴y=-x2+6x-5;
(2)∵△APM和△DPN为等腰直角三角形,
∴∠APM=∠DPN=45°,
∴∠MPN=90°,
∴△MPN为直角三角形.
令-x2+6x-5=0,解得x1=1,x2=5,
∴D(5,0),AD=4.
设AP=m,则DP=4-m,PM=m,PN=(4-m),
∴S△MPN=PM·PN=×m·(4-m)
=-m2+m=-(m-2)2+1,
∴当m=2,即AP=2时,S△MPN最大,此时OP=3,∴P(3,0);
(3)存在,点Q坐标为(2,-3)或.
由A(1,0),B(4,3),C(0,-5),D(5,0),得AB=3,AD=4,直线CD的函数表达式为y=x-5,∴∠BAD=∠CDO=45°,分两种情况讨论:
①当△ADQ∽△DAB时,=,
∴DQ=AB=3,
答图
如答图,过Q点作x轴的垂线,垂足为E,则DE=EQ=DQ=3,
∵D(5,0),∴Q(2,-3);
②当△QDA∽△DAB时,=,
∴=,解得DQ=,
同上得Q坐标为.
综上,存在点Q坐标为(2,-3)或.
5.解:(1)令y=0,得x2-x-4=0,解得x1=-2,x2=3;
令x=0,得y=-4,
故A(-2,0),B(3,0),C(0,-4);
答图①
(2)如答图①,过点Q作QD⊥AB于点D,则AP=2t,BQ=t,BO=3,AB=5,OC=4,BC==5,PB=5-2t.
∵DQ∥OC,
∴△BDQ∽△BOC,
∴=,即=,
解得DQ=t.
∴S△PBQ=PB·DQ=×t×(5-2t)=-t2+2t=-+,
∴当t=时,S△PBQ取最大值为;
答图②
(3)存在,M的坐标为(1,-4)或.
设M,直线BC的表达式为y=kx-4,
则3k-4=0,解得k=,
∴直线BC的表达式为y=x-4,
如答图②,过M作ME⊥AB交BC于点N,则N,
∴MN=m-4-=-m2+2m,
∴S△MBC=S△CMN+S△BMN=MN·OB=-m2+3m,
∵△BMC的面积是△PBQ的面积的1.6倍,
∴-m2+3m=1.6×,整理得m2-3m+2=0,解得m1=1,m2=2.
∴M(1,-4)或.
6.解:(1)由题意知解得
∴抛物线L的表达式为y=-x2+2x+1;
(2)∵y=kx-k+4=k(x-1)+4,
当x=1时,y=4,
∴该直线过定点G(1,4),如答图,
答图
∵y=-x2+2x+1=-(x-1)2+2,
∴点B(1,2),∴BG=2,
∵S△BMN=1,即S△BNG-S△BMG=BG·(xN-1)-BG·(xM-1)=1,
∴xN-xM=1,
由得x2+(k-2)x-k+3=0,
于是xM+xN=2-k,xM·xN=3-k,
故xN-xM==.
由xN-xM=1得=1,
∵k<0,∴k=-3;
(3)设抛物线L1的表达式为y=-x2+2x+1+m,P(0,t),
∴C(0,1+m),D(2,1+m),F(1,0),
当△PCD∽△FOP时,=,
∴=,整理得t2-(1+m)t+2=0;①
当△PCD∽△POF时,=,
∴=,整理得t=(m+1).②
Ⅰ.当方程①有两个相等实数根时,
Δ=(1+m)2-8=0,解得m=2-1(负值舍去),
此时方程①有两个相等实数根t1=t2=,方程②有一个实数根t=,
∴m=2-1,
∴点P的坐标为(0,)或;
Ⅱ.当方程①有两个不相等的实数根时,
把②代入①,得(m+1)2-(m+1)2+2=0,
解得m=2(负值舍去),
此时方程①有两个不相等的实数根t1=1,t2=2,方程②有一个实数根t=1,
∴m=2,
∴点P的坐标为(0,1)或(0,2).
综上,当m=2-1时,点P的坐标为(0,)或;当m=2时,点P的坐标为(0,1)或(0,2).
同课章节目录
