上海市金山中学2015-2016学年高二下学期第一次月考数学试题
文档属性
| 名称 | 上海市金山中学2015-2016学年高二下学期第一次月考数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 417.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-15 13:15:29 | ||
图片预览




文档简介
金山中学2015学年第二学期高二年级第一次段考
数学试卷
(考试时间:120分钟 满分:150分 命题人:李永兰 审核人:袁祎)
一、填空题(本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分。
1.设复数(为虚数单位),则______.
2.圆锥的母线长为,底面直径为,则圆锥的高为______.
3.正方体中,异面直线与所成的角的大小为______.
4.正三棱锥的底面边长为,侧棱长为,则此正三棱锥的高为______.
5.实系数一元二次方程的一个虚根的模是,则实数______.
6.已知是空间四点,命题甲:四点不共面,命题乙:直线和不相交,则甲是乙成立的______条件
7.若四面体的四个面都是等边三角形,则与平面所成角的大小为______.
8.关于的方程的两个根为且,则实数的值______.
9.已知正四棱柱,,为的中点,则直线与平面的距离为______.
10.用一张长、宽分别为和的矩形硬纸折成正四棱柱的侧面,则此正四棱柱的对角线长______.
11.有根细木棒,其中较长的两根分别为,,其余根均为,用它们搭成三棱锥,则其中两条较长的棱所在的直线所成的角的余弦值为______.
12.下面是关于四棱柱的四个命题:
①若有两个侧面垂直于底面,则该四棱柱为直四棱柱
②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱
③若四个侧面两两全等,则该四棱柱为直四棱柱
④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱
其中,真命题的编号是______. (写出所有真命题的编号).
13.长方体中,,一只蚂蚁从点出发沿表面爬行
到点,蚂蚁爬行的最短路线的长为______.
14.如图,在四棱锥中,⊥底面,且底面各边都相等,是上的一动点,当点满足_______时,平面⊥平面 (只要填写一个你认为正确的条件即可).
(第14题图)
二、选择题(本大题满分20分)本大题共有 ( http: / / www.21cnjy.com )4题,每题有且只有一个正确答案,考生必须在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分。
15.下面是关于复数的四个命题:
①; ②; ③的共轭复数为; ④的虚部为.
其中正确的命题…………………………………………………………………( )
A.②③ B.①② C.②④ D.③④
16.已知是两条不同直线,是两个不同平面,下列命题中的假命题的是……( )
A. B.
C. D.
17.在长方体中,,若棱上存在一点,使得⊥,则棱的长的取值范围是………………………………………………( )
A. B. C. D.
18.如图,正方体的棱长为,过点作平面的垂线,垂足为点,则以下命题中,错误的命题是………………………………………………( )
A.点是的垂心 B.垂直于平面
C.延长线经过点 D.直线和所成角为;
(第18题图)
三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤。
19.(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分。
如图所示,在长方体中,,,,为棱上一点.
(1)若,求异面直线和所成角的正切值;
(2)若,求证平面.
20.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分。
已知,且满足.
(1)求;
(2)若,,求证:.
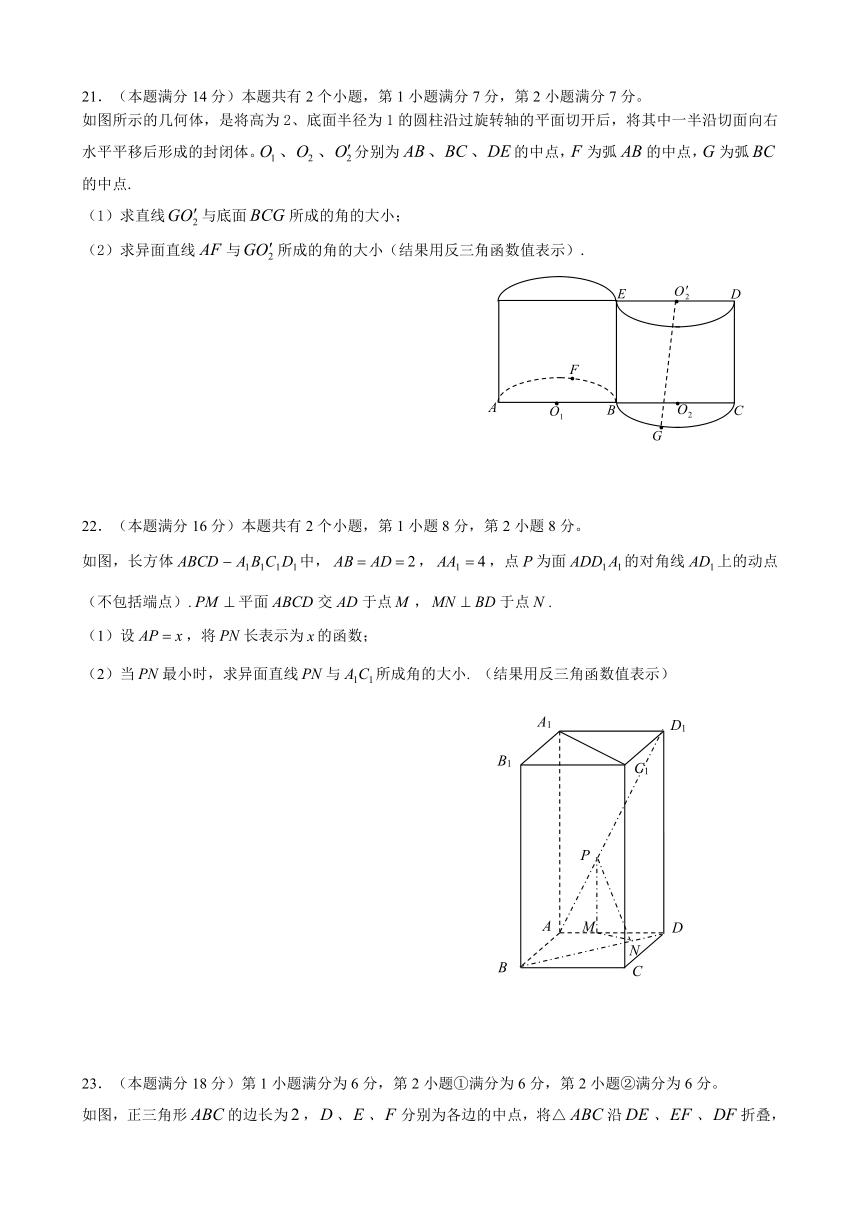
21.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分。
如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体。分别为的中点,为弧的中点,为弧的中点.
(1)求直线与底面所成的角的大小;
(2)求异面直线与所成的角的大小(结果用反三角函数值表示).
22.(本题满分16分)本题共有2个小题,第1小题8分,第2小题8分。
如图,长方体中,,,点为面的对角线上的动点(不包括端点).平面交于点,于点.
(1)设,将长表示为的函数;
(2)当最小时,求异面直线与所成角的大小. (结果用反三角函数值表示)
23.(本题满分18分)第1小题满分为6分,第2小题①满分为6分,第2小题②满分为6分。
如图,正三角形的边长为,、、分别为各边的中点,将△沿、、折叠,使、、三点重合,构成三棱锥.
(1)求平面与底面所成二面角的余弦值;
(2)设点、分别在、上, (为变量) ;
①当为何值时,为异面直线与的公垂线段 请证明你的结论
②设异面直线与所成的角为,异面直线与所成的角为,试求的值.
金山中学2015学年第二学期高二年级段考试卷
(考试时间:120分钟 满分:150分 命题人:李永兰 审核人:袁祎)
一、填空题(本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分。
1.设复数(为虚数单位),则______.
2.圆锥的母线长为,底面直径为,则圆锥的高为______.
3.正方体中,异面直线与所成的角的大小为______.
4.正三棱锥的底面边长为,侧棱长为,则此正三棱锥的高为______.
5.实系数一元二次方程的一个虚根的模是,则实数______.
6.已知是空间四点,命题甲:四点不共面,命题乙:直线和不相交,则甲是乙成立的______条件 充分不必要
7.若四面体的四个面都是等边三角形,则与平面所成角的大小为______.
8.关于的方程的两个根为且,则实数的值______.
9.已知正四棱柱,,为的中点,则直线与平面的距离为______.1
10.用一张长、宽分别为和的矩形硬纸折成正四棱柱的侧面,则此正四棱柱的对角线长______.或
11.有根细木棒,其中较长的两根分别为,,其余根均为,用它们搭成三棱锥,则其中两条较长的棱所在的直线所成的角的余弦值为______.
12.下面是关于四棱柱的四个命题:
①若有两个侧面垂直于底面,则该四棱柱为直四棱柱
②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱
③若四个侧面两两全等,则该四棱柱为直四棱柱
④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱
其中,真命题的编号是______. (写出所有真命题的编号).②④
13.长方体中,,一只蚂蚁从点出发沿表面爬行
到点,蚂蚁爬行的最短路线的长为______.
14.如图,在四棱锥中,⊥底面,且底面各边都相等,是上的一动点,当点满足_______时,平面⊥平面 (只要填写一个你认为正确的条件即可). DM⊥PC(或BM⊥PC)
二、选择题(本大题满分20分)本大题共有4 ( http: / / www.21cnjy.com )题,每题有且只有一个正确答案,考生必须在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分。
15.下面是关于复数的四个命题:
①; ②; ③的共轭复数为; ④的虚部为.
其中正确的命题…………………………………………………………………(C )
A.②③ B.①② C.②④ D.③④
16.已知是两条不同直线,是两个不同平面,下列命题中的假命题的是……( C)
A. B.
C. D.
17.在长方体中,,若棱上存在一点,使得⊥,则棱的长的取值范围是………………………………………………(D )
A. B. C. D.
18.如图,正方体的棱长为,过点作平面的垂线,垂足为点,则以下命题中,错误的命题是………………………………………………(D )
A.点是的垂心 B.垂直于平面
C.延长线经过点 D.直线和所成角为;
三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤。
19.(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分。
如图所示,在长方体中,,,,为棱上一点.
(1)若,求异面直线和所成角的正切值;
(2)若,求证平面.
19. 解:(1)由题意,,,得………… 1分
,所以异面直线和所成角即为和所成角 ………… 3分
长方体中,,面,
,故可得为锐角且…………………… 6分
(2)由题意,,,
,,即 ……………………………… 8分
又由面可得 ………………………………………… 10分
故平面. ………………………………………………………………12分
20.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分。
已知,且满足.
(1)求;
(2)若,,求证:.
20.解:(1)设,则, …………2分
由
得 ……………………………4分
解得 或 ……………………………… 5分
∴或……………………………… 7分
(2)当时,
…………………… 10分
当时,
………………………13分
∴ ……………………………14分
21.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分。
如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体。分别为的中点,为弧的中点,为弧的中点.
(1)求直线与底面所成的角的大小;
(2)求异面直线与所成的角的大小(结果用反三角函数值表示).
21.解:(1) ……7分
(2)连结、、,则,
所以或其补角为异面直线与所成的角. ……9分
在中,,
,………………………………………………12分
因为,
所以.
所以,异面直线与所成的角的大小为.……14分
22.(本题满分16分)本题共有2个小题,第1小题8分,第2小题8分。
如图,长方体中,,,点为面的对角线上的动点(不包括端点).平面交于点,于点.
(1)设,将长表示为的函数;
(2)当最小时,求异面直线与所成角的大小. (结果用反三角函数值表示)
22.解:(1)在△中,,; ………………………( 3分)
其中; ………………………( 4分)
在△中,, …………………………( 6分)
在△中,,……………………………( 8分)
(2)当时,最小,此时.……………………………(10分)
因为在底面中,,所以,又,为异面直线与所成角的平面角,…………………( 13分)
在△中,为直角,,所以,
异面直线与所成角的大小(或等)……………( 16分)
23.(本题满分18分)第1小题满分为6分,第2小题①满分为6分,第2小题②满分为6分。
如图,正三角形的边长为,、、分别为各边的中点,将△沿、、折叠,使、、三点重合,构成三棱锥.
(1)求平面与底面所成二面角的余弦值;
(2)设点、分别在、上, (为变量) ;
①当为何值时,为异面直线与的公垂线段 请证明你的结论
②设异面直线与所成的角为,异面直线与所成的角为,试求的值.
23.解:(1)如图,取DE的中点G,连接AG、FG
由题意AD=AE,△DEF为正三角形,得AG⊥DE,
∴∠AGF为平面ADE与底面DEF所成二面角的平面角
由题意得AG=FG=.在△AGF中,
∴平面ADF与底面DEF所成二面角的余弦值为
(2)①λ=1时,MN为异面直线AD与EF公垂线段
当λ=1,M为AD的中点,N为FF的中点,连结AN、DN,
则由题意,知AN=DN=,∴MN⊥AD,同理可证MN⊥EF
∴λ=1时,MN为异面直线AD与EF公垂线段.
②过点M作MH∥DF,交AF于点H,则∠HMN为异面直线 MN与DF所成的角 .
由MH∥DF,得 ,∴
∴HN//AE,∠MNH为异面直线 MN与AE所成的角 .
∴α+β=∠MNH+∠HMN=π—∠MHN
由题意得,三棱锤A—DEF是正棱锤,则点A在底面DEF上的射影为底面△DEF的中心,记为O.
∵ AE在底面DEF上的射影EO⊥DF, ∴AE⊥DF
又∵HN//AE,MH//DF,∴∠MNH= ,∴
A
B
C
D
A1
B1
C1
D1
P
M
N
A
B
C
D
A1
B1
C1
D1
P
M
N
数学试卷
(考试时间:120分钟 满分:150分 命题人:李永兰 审核人:袁祎)
一、填空题(本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分。
1.设复数(为虚数单位),则______.
2.圆锥的母线长为,底面直径为,则圆锥的高为______.
3.正方体中,异面直线与所成的角的大小为______.
4.正三棱锥的底面边长为,侧棱长为,则此正三棱锥的高为______.
5.实系数一元二次方程的一个虚根的模是,则实数______.
6.已知是空间四点,命题甲:四点不共面,命题乙:直线和不相交,则甲是乙成立的______条件
7.若四面体的四个面都是等边三角形,则与平面所成角的大小为______.
8.关于的方程的两个根为且,则实数的值______.
9.已知正四棱柱,,为的中点,则直线与平面的距离为______.
10.用一张长、宽分别为和的矩形硬纸折成正四棱柱的侧面,则此正四棱柱的对角线长______.
11.有根细木棒,其中较长的两根分别为,,其余根均为,用它们搭成三棱锥,则其中两条较长的棱所在的直线所成的角的余弦值为______.
12.下面是关于四棱柱的四个命题:
①若有两个侧面垂直于底面,则该四棱柱为直四棱柱
②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱
③若四个侧面两两全等,则该四棱柱为直四棱柱
④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱
其中,真命题的编号是______. (写出所有真命题的编号).
13.长方体中,,一只蚂蚁从点出发沿表面爬行
到点,蚂蚁爬行的最短路线的长为______.
14.如图,在四棱锥中,⊥底面,且底面各边都相等,是上的一动点,当点满足_______时,平面⊥平面 (只要填写一个你认为正确的条件即可).
(第14题图)
二、选择题(本大题满分20分)本大题共有 ( http: / / www.21cnjy.com )4题,每题有且只有一个正确答案,考生必须在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分。
15.下面是关于复数的四个命题:
①; ②; ③的共轭复数为; ④的虚部为.
其中正确的命题…………………………………………………………………( )
A.②③ B.①② C.②④ D.③④
16.已知是两条不同直线,是两个不同平面,下列命题中的假命题的是……( )
A. B.
C. D.
17.在长方体中,,若棱上存在一点,使得⊥,则棱的长的取值范围是………………………………………………( )
A. B. C. D.
18.如图,正方体的棱长为,过点作平面的垂线,垂足为点,则以下命题中,错误的命题是………………………………………………( )
A.点是的垂心 B.垂直于平面
C.延长线经过点 D.直线和所成角为;
(第18题图)
三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤。
19.(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分。
如图所示,在长方体中,,,,为棱上一点.
(1)若,求异面直线和所成角的正切值;
(2)若,求证平面.
20.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分。
已知,且满足.
(1)求;
(2)若,,求证:.
21.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分。
如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体。分别为的中点,为弧的中点,为弧的中点.
(1)求直线与底面所成的角的大小;
(2)求异面直线与所成的角的大小(结果用反三角函数值表示).
22.(本题满分16分)本题共有2个小题,第1小题8分,第2小题8分。
如图,长方体中,,,点为面的对角线上的动点(不包括端点).平面交于点,于点.
(1)设,将长表示为的函数;
(2)当最小时,求异面直线与所成角的大小. (结果用反三角函数值表示)
23.(本题满分18分)第1小题满分为6分,第2小题①满分为6分,第2小题②满分为6分。
如图,正三角形的边长为,、、分别为各边的中点,将△沿、、折叠,使、、三点重合,构成三棱锥.
(1)求平面与底面所成二面角的余弦值;
(2)设点、分别在、上, (为变量) ;
①当为何值时,为异面直线与的公垂线段 请证明你的结论
②设异面直线与所成的角为,异面直线与所成的角为,试求的值.
金山中学2015学年第二学期高二年级段考试卷
(考试时间:120分钟 满分:150分 命题人:李永兰 审核人:袁祎)
一、填空题(本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分。
1.设复数(为虚数单位),则______.
2.圆锥的母线长为,底面直径为,则圆锥的高为______.
3.正方体中,异面直线与所成的角的大小为______.
4.正三棱锥的底面边长为,侧棱长为,则此正三棱锥的高为______.
5.实系数一元二次方程的一个虚根的模是,则实数______.
6.已知是空间四点,命题甲:四点不共面,命题乙:直线和不相交,则甲是乙成立的______条件 充分不必要
7.若四面体的四个面都是等边三角形,则与平面所成角的大小为______.
8.关于的方程的两个根为且,则实数的值______.
9.已知正四棱柱,,为的中点,则直线与平面的距离为______.1
10.用一张长、宽分别为和的矩形硬纸折成正四棱柱的侧面,则此正四棱柱的对角线长______.或
11.有根细木棒,其中较长的两根分别为,,其余根均为,用它们搭成三棱锥,则其中两条较长的棱所在的直线所成的角的余弦值为______.
12.下面是关于四棱柱的四个命题:
①若有两个侧面垂直于底面,则该四棱柱为直四棱柱
②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱
③若四个侧面两两全等,则该四棱柱为直四棱柱
④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱
其中,真命题的编号是______. (写出所有真命题的编号).②④
13.长方体中,,一只蚂蚁从点出发沿表面爬行
到点,蚂蚁爬行的最短路线的长为______.
14.如图,在四棱锥中,⊥底面,且底面各边都相等,是上的一动点,当点满足_______时,平面⊥平面 (只要填写一个你认为正确的条件即可). DM⊥PC(或BM⊥PC)
二、选择题(本大题满分20分)本大题共有4 ( http: / / www.21cnjy.com )题,每题有且只有一个正确答案,考生必须在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分。
15.下面是关于复数的四个命题:
①; ②; ③的共轭复数为; ④的虚部为.
其中正确的命题…………………………………………………………………(C )
A.②③ B.①② C.②④ D.③④
16.已知是两条不同直线,是两个不同平面,下列命题中的假命题的是……( C)
A. B.
C. D.
17.在长方体中,,若棱上存在一点,使得⊥,则棱的长的取值范围是………………………………………………(D )
A. B. C. D.
18.如图,正方体的棱长为,过点作平面的垂线,垂足为点,则以下命题中,错误的命题是………………………………………………(D )
A.点是的垂心 B.垂直于平面
C.延长线经过点 D.直线和所成角为;
三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤。
19.(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分。
如图所示,在长方体中,,,,为棱上一点.
(1)若,求异面直线和所成角的正切值;
(2)若,求证平面.
19. 解:(1)由题意,,,得………… 1分
,所以异面直线和所成角即为和所成角 ………… 3分
长方体中,,面,
,故可得为锐角且…………………… 6分
(2)由题意,,,
,,即 ……………………………… 8分
又由面可得 ………………………………………… 10分
故平面. ………………………………………………………………12分
20.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分。
已知,且满足.
(1)求;
(2)若,,求证:.
20.解:(1)设,则, …………2分
由
得 ……………………………4分
解得 或 ……………………………… 5分
∴或……………………………… 7分
(2)当时,
…………………… 10分
当时,
………………………13分
∴ ……………………………14分
21.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分。
如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体。分别为的中点,为弧的中点,为弧的中点.
(1)求直线与底面所成的角的大小;
(2)求异面直线与所成的角的大小(结果用反三角函数值表示).
21.解:(1) ……7分
(2)连结、、,则,
所以或其补角为异面直线与所成的角. ……9分
在中,,
,………………………………………………12分
因为,
所以.
所以,异面直线与所成的角的大小为.……14分
22.(本题满分16分)本题共有2个小题,第1小题8分,第2小题8分。
如图,长方体中,,,点为面的对角线上的动点(不包括端点).平面交于点,于点.
(1)设,将长表示为的函数;
(2)当最小时,求异面直线与所成角的大小. (结果用反三角函数值表示)
22.解:(1)在△中,,; ………………………( 3分)
其中; ………………………( 4分)
在△中,, …………………………( 6分)
在△中,,……………………………( 8分)
(2)当时,最小,此时.……………………………(10分)
因为在底面中,,所以,又,为异面直线与所成角的平面角,…………………( 13分)
在△中,为直角,,所以,
异面直线与所成角的大小(或等)……………( 16分)
23.(本题满分18分)第1小题满分为6分,第2小题①满分为6分,第2小题②满分为6分。
如图,正三角形的边长为,、、分别为各边的中点,将△沿、、折叠,使、、三点重合,构成三棱锥.
(1)求平面与底面所成二面角的余弦值;
(2)设点、分别在、上, (为变量) ;
①当为何值时,为异面直线与的公垂线段 请证明你的结论
②设异面直线与所成的角为,异面直线与所成的角为,试求的值.
23.解:(1)如图,取DE的中点G,连接AG、FG
由题意AD=AE,△DEF为正三角形,得AG⊥DE,
∴∠AGF为平面ADE与底面DEF所成二面角的平面角
由题意得AG=FG=.在△AGF中,
∴平面ADF与底面DEF所成二面角的余弦值为
(2)①λ=1时,MN为异面直线AD与EF公垂线段
当λ=1,M为AD的中点,N为FF的中点,连结AN、DN,
则由题意,知AN=DN=,∴MN⊥AD,同理可证MN⊥EF
∴λ=1时,MN为异面直线AD与EF公垂线段.
②过点M作MH∥DF,交AF于点H,则∠HMN为异面直线 MN与DF所成的角 .
由MH∥DF,得 ,∴
∴HN//AE,∠MNH为异面直线 MN与AE所成的角 .
∴α+β=∠MNH+∠HMN=π—∠MHN
由题意得,三棱锤A—DEF是正棱锤,则点A在底面DEF上的射影为底面△DEF的中心,记为O.
∵ AE在底面DEF上的射影EO⊥DF, ∴AE⊥DF
又∵HN//AE,MH//DF,∴∠MNH= ,∴
A
B
C
D
A1
B1
C1
D1
P
M
N
A
B
C
D
A1
B1
C1
D1
P
M
N
同课章节目录
